Mathematica Eterna
Open Access

A Clustering-Based Multiple Kernel Learning Algorithm for Multi-Class-Review Article Classification

Zhang Xiaofeng^{* *}Correspondence: Zhang Xiaofeng, Department of Economics and Management, Jiangsu Institute of Administration, Nanjing 210009, China, Email:

Author info »

Introduction

Multiple kernel learning algorithms have been widely studied recently. It uses a set of base kernel functions combined linearly or nonlinearly. This combination constitutes a kernel combination function for learning. Multiple kernel learning works in the combination space made by multiple features. It uses the mapping ability of each base kernel function. This lets the data be more accurately expressed in the combination feature space. This is a good fix for the problem of weak base kernel function representation ability [1]. This method suits large-scale samples and those with diverse information. It also works with highdimensional data that’s not flat. Multiple Kernel Learning (MKL) algorithms are popular in multi-view, object recognition, hyperspectral image classification and other task areas [2-4]. It has three optimization objective functions: Similarity measure, structural risk minimization, and Bayesian function. Those functions are solved by one-step or two-step learning methods. One-step method solves basis kernel function parameters and weight vectors simultaneously, needing Semidefinite Programming solution (SDP), Quadratic Constrain Quadratic Programming (QCQP) or complex optimization forms such as Second-Order Cone Programming (SOCP) [5-7]. The twostep learning method needs inner and outer iterations to solve parameters. It solves for the basis kernel function and its weight vectors, respectively. One-step and two-step methods all have high time complexity [8]. In contrast, Bayesian function optimization requires Gibbs sampling. This is to construct the objective function. It needs to find approximate solutions [9]. Lanckriet et al., constructed an SDP problem form using multiple kernel learning and later constructed a QCQP problem form [5]. Sonnenburg et al., transformed the multiple kernel learning SDP and QCQP problem forms to obtain a Semi-infinite Linear Programming (SILP) form [10]. Bach et al., proposed a problem form using SOCP [7]. Rakotomamonjy et al.. introduced SimpleMKL, a twostep algorithm solving SVMs [11]. Girolami et al., built a Bayesian hierarchical model and derived parameters [12]. They used kernel combinatorial functions in Gaussian processes to define weighted variance matrices. These matrices combined data from different sources. They then performed joint inference for Gaussian process and kernel combinatorial parameters [13]. In the last decade, multiple kernel learning developed extended MKL methods. Localized MKL derives kernel weight vectors by localizing the effect [14]. Sampleadaptive MKL specifies kernel switches for different sample switches [15]. Bayesian MKL formulates kernel combinations through a Bayesian approach [16]. Function approximation MKL uses function approximation to find the optimal kernel function [17]. These methods include extended forms for different tasks. We propose a novel Clustering-Based Multiple Kernel Learning (CBMKL) algorithm for multi-class classification in this paper. This approach constructs a clustering-based objective function using multiple kernel properties. The idea combines clustering and classification problems, treating classification as unsupervised clustering. This allows using the clustering objective function to construct the multi-class classification one. To unify clustering algorithms, kernel clustering mapping requires kernel function embedding. The kernel function projects input space to a highdimensional feature space. Derivation shows the clustering objective function works for multi-class classification here. This CBMKL algorithm has several advantages.

• It handles multi-class problems directly, unlike most MKL algorithms. They only handle binary classification directly, though they can adapt to multi-class using methods like One- VS-All.

• This algorithm has an analytical solution, avoiding approximate solutions from sampling methods.

• It also has polynomial time complexity. Here is the organization of this paper: Related works covers three classes of optimization objective functions in multiple kernel learning algorithms and related research. A Clustering-based Multiple Kernel Learning algorithm for multi-class classification (CBMKL) adapts the clustering problem objective function for multi-class classification and introduces a novel CBMKL algorithm. Experiment and analysis tests the proposed method on handwritten digit and relational extraction datasets. Finally, conclusion summarizes the paper and suggests future work directions.

Material and Methods

Related works

The first method for building multiple kernel learning algorithms’ objective functions uses similarity measure law. Shawe-Taylor proposed an algorithm measuring kernel function similarity called kernel alignment [18]. Given the kernel functions k1 and k2, compute the empirical kernel arrangement as follows:

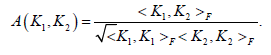
Where, F denotes the Frobenius paradigm, i.e.

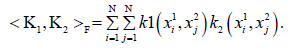
The norm represents the angle cosine between k1 and k2.

yy^T is called the ideal kernel. Define an arrangement between the candidate kernel and ideal kernel as:

 

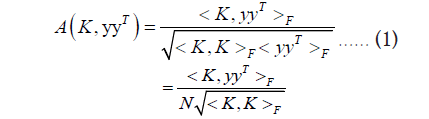
From Equation 1, the maximum kernel alignment value can be obtained when the candidate kernel is sufficiently fitted to the ideal kernel. Therefore, the kernel alignment is introduced into multiple kernel learning to learn the kernel combination weight vector, Lanckriet et al., take max A(K, yy^T ) as the optmization objective function, which gives the following optimization equation [5]:

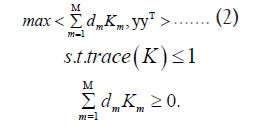
Where, trace (K) denotes the trace of Kernel combination matrix K. denotes the matrix K satisfies the semi-positive definite condition.

Cortes et al., used the cantered kernel alignment values as a similarity metric between candidate and ideal kernels [19]. Their optimization objective is max CA(K^c , yy^T ) . Where CA(K^c , yy^T )denotes the Cantered Kernel alignment value, and Kc denotes centralizing the kernel combination matrix K, i.e.

Where, l is the number of training samples, and 1 denotes a vector whose elements are all 1. Notice that the y of kernel alignment can only take values for each element of 1, so it is only directly applicable to binary classification problems. Lanckriet et al., Express the multiple kernel learning optimization formulation of Equation 2 in the following Semidefinite Programming Problem (SDP) form [5]:

Lanckriet et al., also restricted the basis kernel function weight vector in the semidefinite programming problem of Equation 3 to nonnegative values and transformed it into a quadratically constrained quadratic programming problem (QCQP) [6]:

eThe second idea of constructing the objective function of a multiple kernel learning algorithm comes from the classical law of machine learning-structural risk minimization, which is to reduce the VC dimension of the learning machine while guaranteeing the classification accuracy (empirical risk) so that the learning machine expects the risk to be controlled over the entire sample set. Rakotomamonjy et al. have taken the kernel combining function K embedded by the feature space mapping φ (x) , substituting it into the single kernel learning optimization equation [11]:

Then the multiple kernel learning optimization objective function is:

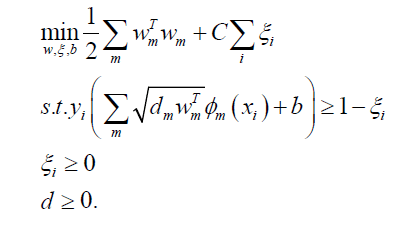
By transforming it into a convex optimization form and solving it in dyadic space using Lagrangian functions, the final requirement to solve the optimization problem can be obtained as follows:

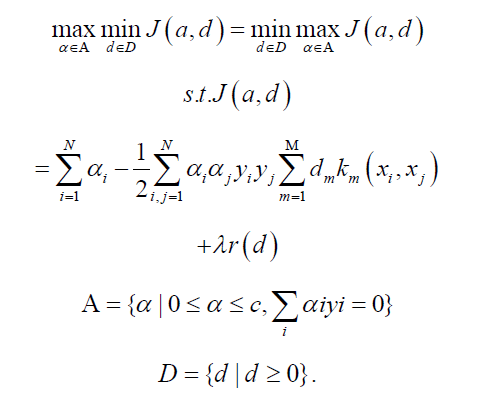
Sonnenburg et al., transformed the above form of the QCQP problem into the form of the SILP problem [10]:

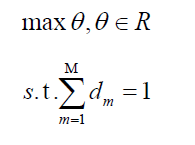
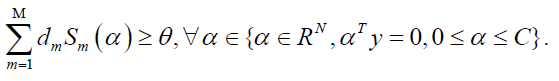
Among them,

Bach et al., construct the SOCP problem form as follows [7]:

In the above optimization model solving, either using a one-step or two-step method time complexity is higher, which is determined by the inherent complexity of the model. The third objective function of multiple kernel learning algorithm construction is based on the Bayesian approach. The Bayesian approach treats the weight vector of the basis kernel function as a random variable with some prior probability distribution, and then the weight vector and the parameters of the basis kernel function are derived through inference. Girolami et al. propose a decision function shaped like this [12]:

Where, d obeys a Dirichlet prior from a Gaussian distribution with mean 0 and a reversible prior variance [12]. The algorithm performs tasks such as classification or clustering by inference through a variational bayesian approach. Girolami et al. later extended the algorithm by adding auxiliary variables to obtain a valid Gibbs sampling using polynomial likelihood [13]. Bayesian

based methods can only yield approximate solutions and not analytic solutions. As for some other extended MKL optimization objective functions, they will not be repeated as they are not very relevant to the topic of this paper.

A Clustering-Based Multiple Kernel Learning algorithm for multi-class classification (CBMKL)

Measures of clustering models: Clustering and categorization are similar tasks in machine learning. Both find a mapping from training samples to categories. However, the key difference is that clustering is an unsupervised learning problem with unknown category numbers. Good and bad criteria for both models exist, keeping different category samples separate [20]. This principle is seen in classification problems and SVM maximum spacing principle [21]. It’s more complex in clustering, discussed below.

[Clustering Task Formalization] The clustering task is given an unlabelled dataset S = {x1 , x2 ,..., x1 }that finds a mapping f : S →{1, 2,..., N}. The clustering objective function depends on two factors. First, to meet the same category of training samples can be close enough to each other, that is, training samples within the class distance should be as small as possible. Second, the training samples of different categories should be separated enough, i.e., the distance between training samples should be as large as possible. A good clustering model should take both into account. [Clustering Model Measurement 1] A good clustering model should satisfy

Where φ (x) is the projection function on the feature space F. Equation 4 contains two parts of the algebraic sum of the arithmetic. The former is the training sample intra-class distance, while the latter is the training sample inter-class distance. λ is the trade-off value. Derivation of the latter term of Equation 4.

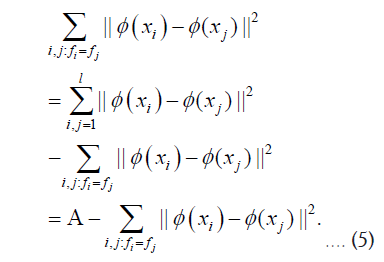
Where, A is a constant when the data set is given. Substituting Equation 5 into Equation 4 yields

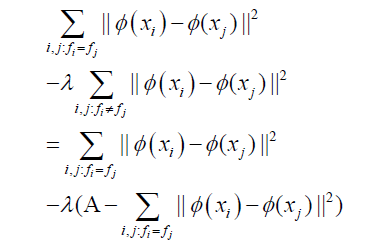
Thus Equation 4 can be expressed as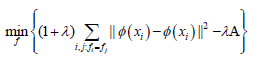

This gives another measure of how good the clustering model is, as follows:

(Clustering model measurement 2) A good clustering model should satisfy [21]

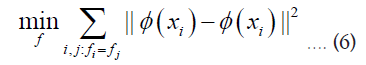
Equation 6 contains only the calculation of the training sample intra-class distances and does not require the calculation of the training sample inter-class distances.

Optimizing the objective function: If the number of training set classes is given, a key difference disappears. The second difference is clear from Equation 6: Small intra-class distances ensure large interclass distances. This analysis leads to a new approach: combining multiple kernel learning, converting classification to clustering, and using clustering measures as optimization objectives, yielding a clustering-based multi-class classification algorithm. Given a labelled dataset

Where x^_i(n) denotes the i training samples of the n class, and is the number of training samples in the n class. The kernel combination function , where Km is the basis kernel function, and d is the weight vector. φ (x) is the Eigen function of matrix K, and the derivation of Equation 6 is performed:

Minimizing Equation 7 is the optimization objective for the multi-class classification task proposed in this paper. Thus, the Clustering-Based Multiple Kernel Learning algorithm for multiclass classification (CBMKL) can be formalized as the following constrained optimization problem:

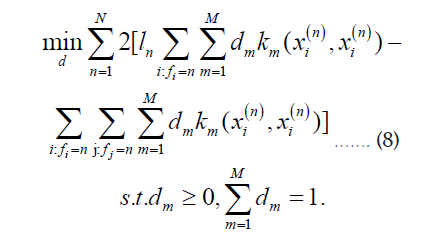
Solution of the optimizing problem: When the base kernel k_m is given case, despite the complex form of Equation 8, it is in essence a 1 l paradigm 1 (|| d || =1) constrained linear optimization problem. The proof is as follows:

The solution process begins with the given K_m premise, calculate 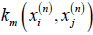and the corresponding 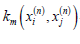values of the equation,where, i, j =1,.....,l_n, n=1...., N .

Then calculate Equation 8 by algebra and expression of the d_m coefficients, where m=1…,M. Currently, the optimization objective of Equation 8 is shaped as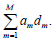

Among the above equation, am is the coefficient of dm, m=1…,M. which takes on real numbers. Then the following optimization problem is posed:

3 Equation 9 is a l1paradigm 1 (|| d ||₁ =1) linear programming problem under constraints, and the optimal analytical solution can be obtained by the simplex method [22]. In summary, it is easy to know that the solution time complexity of the optimization problem of Equation 8 is mainly reflected in the calculation of the coefficients, the time complexity of this step is 0 (n²). The time complexity of solving the linear programming problem by the simplex method is as follows 0 (m²) (Although the general time complexity of the linear programming problem using the simplex method is exponential level, here is a degenerate linear programming problem, which is easier to solve, the time complexity is only polynomial level), then the overall time complexity is 0 (n²)+0 (m²). Since 0 (n²)>> 0 (m²), So the overall time complexity of solving this optimization problem is polynomial time 0 (n²).

Classification decision functions: The CBMKL algorithm for multi-class classification optimizes the objective function, i.e., Equation 8 contains only the basis kernel function km and weight vector d and does not contain the SVM decision hyperplane f (x) =< w,φ (x) > + b . Therefore, by solving the optimization equation, only the weight vectors d can be obtained, which leads to the inability to use the decision hyperplane to give test sample labels and other discriminative methods must be used. In this regard, according to the clustering perspective proposed in this paper, the classification problem is still regarded as a clustering problem, and a similar clustering task nearest-neighbour algorithm is used to calculate the distance of test samples to the centers of various classes, and the shortest class label is taken as the label of test samples. The classification decision function proposed in this paper is derived as follows: The center of the n class centers can be calculated by the following equation

Although the mapping function φ is unknown, it is still possible to compute its paradigm using the kernel definition [23], i.e.

Then the distance between test sample (x) φ and the n class center φ_n can be calculated by the following equation:

Thus, the classification decision function f (x) satisfies the following optimization equation:

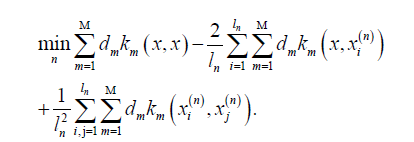
Algorithm I.

A Cluster-based Multiple Kernel Learning algorithm for multi-class classification (CBMKL).

Require. Training data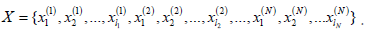

Base kernel functions Km Pre-processing.

Training: Solve the optimization problem below to get weights d_m of base kernel functions K_m

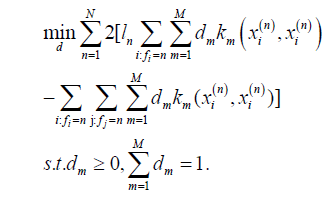
Testing: Solve the optimization problem below to get the label of testing data x;

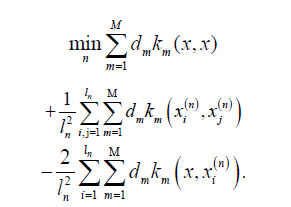
Ensure: Testing data’s label n

It is easy to know that this classification decision function only needs to combine the training data X and the base kernel function K_m and the weight vector d of the base kernel obtained through training. In summary, this paper proposes a Clustering-Based Multiple Kernel Learning algorithm for multi-class classification (CBMKL) as shown in Algorithm I. Algorithm I. begins by substituting a training sample to solve for a l1 Paradigm 1 (|| d ||₁=1) constrained linear programming problem to obtain the basis kernel function K_m and weight vector d and then substituting the test samples into the classification decision function to obtain their category labels.

Results and Discussion

Experiment and analysis

The CBMKL algorithm proposed in this paper has the advantages of simple optimization objective functions and low time complexity for solving the optimization problems, thus adapting to relation extraction applications. To this end, this paper conducts two sets of comparison experiments on the UCI handwritten digit recognition dataset-Pendigits (STA8)1 and the relation extraction dataset Conll042 for validation

Experimental procedures: This paper improves experiment accuracy with single kernel clustering function results. It takes consistent samples from the clustered data to form a new dataset. The paper’s learning algorithm classifies this new dataset. The single kernel function is expanded to form a multiple kernel function. This paper compares experimental results from different multiple kernel learning algorithms. Two sets of experiments are described next.

Handwritten digit recognition experiment on UCI dataset:

Experimental setup: The UCI Handwritten Digit Recognition DatasetPendigits (STA8) contains digits 0 to 9, a total of 10 categories. Each sample has a 64-dimensional eigenvector, obtained from the 8 × 8 bitmap matrix data, totalling 10992 samples, where the training set has 7494 samples and the test set has 3498 samples. Considering the property that the feature space possessed by the Gaussian kernel function is of infinite dimension, any dataset must be linearly divisible in this dimension space [23]. In our experiment, the Gaussian kernel function is firstly used for single kernel clustering operation, respectively, using the standard deviation of σ =0.01, 0.1, 1, 10, and 100 to carry out the test. After testing the standard deviation, the best clustering result σ =0.1 is achieved. Then compare the clustering results with the training set, for a class of clustering that contains the most samples of a certain class in the training set, the class label of that class is used as the label of those samples. Samples that do not meet the above requirements are removed. This is done until all clusters are processed and the result is obtained as an intermediate data set to be processed in the next step. According to the formal characteristics of the algorithm, to calculate conveniently, then categorizes the intermediate dataset samples according to their labels and uses 0 to 9 order in sequence. Next sets the intermediate dataset samples in the σ =0.1 neighbourhood, every 0.01 obtains new values, and those Gaussian kernel functions (from σ =0.01 to σ =0.20, a total of 20) are formed, and finally trained using the algorithm proposed in this paper, and the model parameters are obtained and then validated on the test set. In this paper, we compare the obtained experimental results with some other multiple kernel learning algorithms, focusing on the test accuracy metrics. To ensure experimental comparability, we compare the experimental results given by Gonen et al., for the same dataset on the Matlab platform [8].

Experimental results and analysis: Table 1, gives the experimental results of the UCI handwritten digit recognition dataset. Where ABMKL denotes the kernel alignment algorithm proposed by Lanckriet et al., CABMKL denotes the cantered kernel alignment algorithm proposed by Cortes et al., SimpleMKL denotes the simple multiple kernel learning algorithm proposed by Rakotomamonjy et al., GMKL denotes the generalized multiple kernel learning algorithm proposed by Varma et al., CBMKL (Ours) denotes the clustering based multiple kernel learning algorithm for multi-class classification proposed in this paper [5,11,19,24]. The performance of the CBMKL algorithm can be seen in Table 1, where the precision, recall, and F1 values are slightly higher than other multiple kernel learning algorithms. It indicates that the CBMKL algorithm better represents the high-dimensional feature space and can reflect the potential structure of the latent data. This shows that the CBMKL algorithm is a better-performing multiple kernel learning algorithm for multi-class classification tasks.

Table 1: Comparison of classification performance between clustering-based multiple kernel learning model and other multiple kernel learning algorithms on pendigits (sta8) dataset.

Relational extraction experiments on the conll04 dataset:

Experimental setup: The Conll04 dataset is a benchmark dataset for entity recognition and relation extraction. The dataset collects entities and their relationships in news reports and provides for training and testing algorithm annotation. The Conll04 dataset consists of sentences annotated with entities and interentity relationships with a total of 5516 samples. The number of entities included in it are, Person (1691), Location (1968), and Organization (984), and the number of inter-entity relationships are Located in (406), work for (401), Organbased_in (452), Live_in (529) and Kill (268). There is also a special class of relations Other (706), which is used to represent relations other than the above five. In this paper, we first pre-process this dataset by removing the other relation samples, and for the remaining samples, we utilize grammatical rules (e.g., N-grams and lexical annotations, etc.) to transform them into 101 dimensional feature vectors [25]. We then conduct experiments using the same steps as the UCI handwritten digit recognition set described above and compare the results with existing experiments on this dataset by Roth et al., and Kate et al., [26,27].

Experimental results and analysis: Table 2, gives the results of the experiments on relational extraction for the Conll04 dataset. Where ILP denotes the Integer Linear Programming algorithm proposed by Roth et al., CP denotes the Card Pyramid algorithm proposed by Kate et al., and CBMKL (Ours) denotes our algorithm [26,27]. The experimental results give the relationship between various types of entities F1 values. As can be seen from Table 2, the CBMKL achieves better results in the five groups experiments. Except the relation of Organ based in, other four groups of relationships achieve better results than or slightly inferior to other control algorithms. It shows that the CBMKL algorithm can perform well in most cases, and it is a more stable algorithm. From the above experimental results comparing on Pendigits (STA8) dataset and Conll04 dataset, the algorithm CBMKL proposed in this paper, compared with some common MKL algorithms, has higher precision, recall, and F1 value on different datasets, despite the different optimization objective functions and optimization problems to be solved. It is fully demonstrated that it is a better generalized multiple kernel learning algorithm.

Table 2: Comparison of classification performance of clustering-based multiple kernel learning model with other classification algorithms on the Conll04 dataset.

Conclusion

This paper proposes CBMKL, a new algorithm that analyses clustering and classification tasks. The CBMKL algorithm constructs a new optimization objective function using multiple kernel learning the ory. It provides a new method for solving multiclass classification problems. Compared to previous algorithms, our CBMKL algorithm finds an analytical solution in polynomial time with good performance. In the future, we can simplify data pre-processing by using multiple kernel function clustering. We can also reduce the impact of misclassified samples on clustering center offset.

Declarations

Authors contribution statement

Zhang xiaofeng contributed to the conception of the study, performed the experiment and contributed significantly to analysis and manuscript preparation.

Competing interests

The authors have no competing interests to declare that are relevant to the content of this article.

Data availability and access

Pendigits: http://mkl.ucsd.edu/dataset/pendigits.

Conll04: http://l2r.cs.uiuc.edu/?cogcomp/Data/ER/conll04.corp.

References

1. Lee WJ, Verzakov S, Duin RP. Kernel combination versus classifier combination. Spring Berli Heidelb. 2007:22-31. [Crossref]

   [Google Scholar]

2. de Sa VR, Gallagher PW, Lewis JM, Malave VL. Multi-view kernel construction. Mach Learn. 2010;79(1):47-71.

   [Crossref] [Google Scholar]

3. Bucak SS, Jin R, Jain AK. Multiple kernel learning for visual object recognition: A review. IEEE. 2013 4;36(7):1354-1369.

   [Crossref] [Google Scholar]

4. Liu T, Gu Y. Multiple kernel learning for hyperspectral image classification. Springer. 2020:259-293.

   [Crossref] [Google Scholar]

5. Lanckriet GR, Cristianini N, Bartlett P, Ghaoui LE, Jordan MI. Learning the kernel matrix with semidefinite programming. J Mach Learn Res. 2004;27-72.

   [Google Scholar]

6. Lanckriet GR, de Bie T, Cristianini N, Jordan MI, Noble WS. A statistical framework for genomic data fusion. Bioinform. 2004;20(16):2626-2635.

   [Crossref] [Google Scholar]

7. Bach FR, Lanckriet GR, Jordan MI. Multiple kernel learning, conic duality, and the SMO algorithm. Proc Intern Confer Mach Learn .2004.

   [Crossref] [Google Scholar]

8. Gonen M, Alpaydın E. Multiple kernel learning algorithms. J Mach Learn Res. 2011;12:2211-2268. 

   [Google Scholar]

9. Bishop CM. Pattern recognition and machine learning. Springer. 2006;2:1122-8.

   [Google Scholar]

10. Sonnenburg S, Rätsch G, Schäfer C. Advances in neural information processing systems. 2005;18.

    [Google Scholar]

11. Rakotomamonjy A, Bach F, Canu S, Grandvalet Y. SimpleMKL. J Mach Learn Res. 2008;9:2491-2521.

    [Google Scholar].

12. Girolami M, Rogers S Hierarchic. Bayesian models for kernel learning. Proc Intern Confer Mach Learn. 2005;241-248.

    [Crossref] [Google Scholar]

13. Girolami M, Zhong M. Data integration for classification problems employing Gaussian process priors. Adv Neural Inform Proces Sys. 2006;19.

    [Crossref] [Google Scholar]

14. Chamakura L, Saha G. Localized multiple kernel learning using graph modularity. Pattern Recognit Lett. 2022;155:27-33.

    [Crossref] [Google Scholar]

15. Gu Y, Liu H. Sample-screening MKL method via boosting strategy for hyperspectral image classification. Neurocomput. 2016;173:1630-1639.

    [Crossref] [Google Scholar]

16. Gonen M. Bayesian efficient multiple kernel learning. Arxiv. 2012.

    [Crossref] [Google Scholar]

17. Shiju SS, Sumitra S. Multiple kernel learning using single stage function approximation for binary classification problems. Int J Syst Sci. 2017;48(16):3569-3580.

    [Crossref] [Google Scholar] .

18. Cristianini N, Shawe-Taylor J, Elisseeff A, Kandola J. On kernel-target alignment. Adv Neural Inf Process Syst. 2001;14.

    [Crossref] [Google Scholar]

19. Cortes C, Mohri M, Rostamizadeh A. Two-stage learning kernel algorithms. Proce Intern Confer Mach Learn. 2010; 239-246.

    [Google Scholar]

20. Jain AK, Murty MN, Flynn PJ. Data clustering: A review. Comput Surv. 1999;31(3):264-323.

    [Crossref] [Google Scholar]

21. Cristianini N, Shawe-Taylor J. An introduction to support vector machines and other kernel-based learning methods. Camb Univ Press. 2000.

    [Crossref] [Google Scholar]

22. Bertsekas D, Nedic A, Ozdaglar A. Convex analysis and optimization. Athena Sci. 2003.

    [Google Scholar]

23. Shawe-Taylor J. Kernel methods for pattern analysis. Camb Univ Press. 2004;2:181-201.

    [Crossref] [Google Scholar]

24. Varma M, Babu BR. More generality in efficient multiple kernel learning. Proce Intern Confer Mach Learn. 2009;1065-1072.

    [Crossref] [Google Scholar]

25. Zhang M, Zhou G, Aw A. Exploring syntactic structured features over parse trees for relation extraction using kernel methods. Inf Process Manage. 2008;44(2):687-701.

    [Crossref] [Google Scholar]

26. Roth D, Yih WT. A linear programming formulation for global inference in natural language tasks. Proce Eigh Conf Comput Nat Lang Learn. 2004; 1-8

    [Google Scholar]

27. Kate R, Mooney R. Joint entity and relation extraction using card-pyramid parsing. Proce Fourt Confe Computat Nat Lang Learn. 2010;203-212.

    [Google Scholar]