Mathematica Eterna
Open Access

Does There Really Exist Any Generic Algorithm for Bellmans Lost in Forest Problem

Dutta S^{* *}Correspondence: Dutta S, Department Mathematics, West Bengal University of Technology, India, Email:

Author info »

Introduction

Bellman's lost-in-a-forest problem is a minimization problem in geometry which is considered as unsolved till date. It was first originated in 1955 by the American applied mathematician Richard E. Bellman [1].

The problem is phrased as follows: "A hiker is lost in a forest whose shape and dimensions are precisely known to him. What is the best path for him to follow to escape from the forest?" [2] It is generally considered that the traveler does not know the starting point or direction he is facing.

The best path is considered to be the one that minimizes the worst-case distance to travel before reaching the edge of the forest.

Solution is known for only a few shapes or classes of shape [3]. A generic solution would be in the form of a geometric algorithm which takes the shape of the forest as input and produces the optimal escape route as the output.

Theorem 1

In Euclidean plane consider a closed region or forest whose shape and dimensions are known, if there are no dedicated paths amongst which we need to find any minimal path then there does not exist any generic algorithm which produces a minimal escape path provided that the starting position and the direction from starting position are not known.

Proof

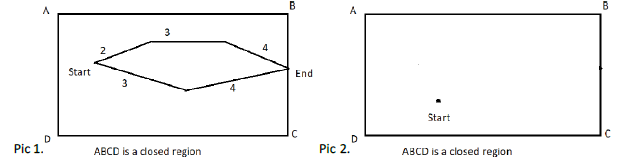
Let R be a closed region and in region R there is no dedicated paths amongst which we need to select the optimal path. So it clearly indicates that we can have paths which can be situated anywhere in the region. Let’s explain this with the help of below pictures, see Pic1, Pic2. In Pic1, ABCD is a closed region where there are two dedicated weighted paths: 2-3-4 and 3-4 from starting point. We can easily select the optimal path 3-4 from these paths using various available shortest path algorithms. Pic2 depicts that ABCD is a closed region and only the starting point is given but starting point may be anywhere and in any direction in the closed region ABCD. From the starting position any path in any direction can be placed and we need to find out the optimal escape route.

Let there exists a generic algorithm G of finite steps, G takes only the shape and dimension of the closed region R as arguments and produces an optimal path from the starting point.

It’s very easy to understand that the optimal path which is a continuous path will consist of:

a. Only curves or,

b. Curves along with Straight lines or,

c. Only straight lines

Consider Case ‘a’: If G produces an optimal path which consists of only curves, and then we can have another algorithm G1:

Step#1: Include all steps of G,

Step#2: Connect the end points of the curves with straight lines.

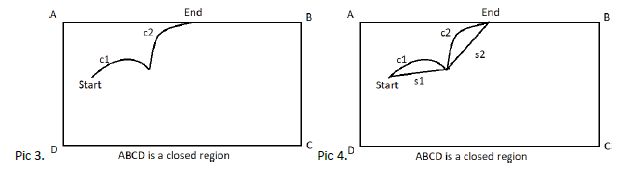
Then G1 will produce a path which is shorter than the optimal path G produces. For better understanding see “Pic3” which depicts the optimal path produced by G with two curves c1 & c2 and see “Pic4” which shows the optimal path which is generated by G1 by connecting the endpoints of the curves c1 & c2 with straight lines s1 & s2 accordingly. Since the minimum distance between two pints in a plain is straight line which connects those two points, hence:

Length of s1 + Length of s2 < Length of c1 + Length of c2, which leads to a contradiction that G produces the optimal path.

Consider Case ‘b’: If G produces an optimal path which consists of curves along with Straight lines, then we can have another algorithm G1:

Step#1: Include all steps of G,

Step#2: Connect the end points of the curves with straight lines.

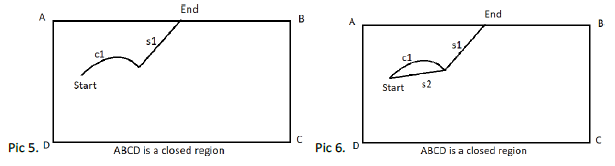
Then G1 will produce a path which is shorter than the optimal path G produces. For better understanding see “Pic5” which depicts the optimal path produced by G with curve c1 and straight line s1 and see “Pic6” which shows the optimal path which is generated by G1 by connecting the endpoints of the curve c1 with straight line s2. Since the minimum distance between two pints in a plain is straight line which connects those two points hence:

Length of s1 + Length of s2 < Length of c1 + Length of s1, which leads to a contradiction that G produces the optimal path.

Consider Case ‘c’: If G produces an optimal path which consists of only straight lines then there might be two cases: One optimal path may be non-linear path consists of straight lines and the other will be only a straight line, see “Pic7” & “Pic8”.

For the first case when the optimal path will be non-linear consists of straight lines then we can have another algorithm G1:

Step#1: Include all steps of G,

Step#2: Connect the starting point of a straight line with the end point of the associated straight lines with straight lines.

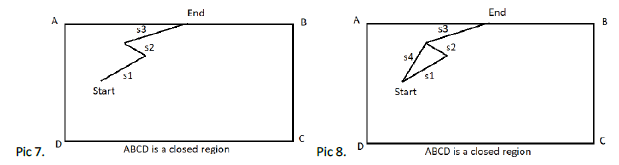
Then G1 will produce a shorter path than the optimal path G produces, see “Pic7” which produces path consists of three straight lines s1-s2-s3. Pic8 depicts the optimal path generated by G1 by connecting the starting position of s1 and end position of s2 with straight line s4. We know that in a triangle the sum of length of two sides is greater than the third side, hence by using Triangular inequality theorem:

Length of s1+ length of s2 > Length of s4,

So Length of s3 + Length of s4 < Length of s1+ length of s2 + Length of s3, which leads to a contradiction that G produces the optimal path.

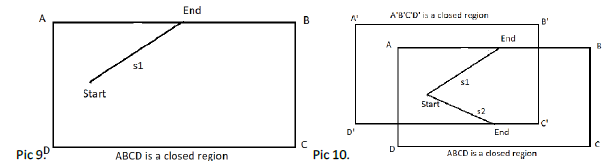
So we are left with only the last option that the optimal path is only a straight line and that can’t be further minimized, see Pic9 which depicts the optimal path as a straight line s1. To discard this case also, we introduce below scenario:

See Pic10 which depicts that ABCD and A’B’C’D’ are two closed regions of same shape and dimensions and they overlap each other i.e. share a common region.

Consider the starting point in the common region. Let algorithm G takes the shape and dimensions of closed region ABCD as argument and produces s1 as optimal path and algorithm G1 takes shape and dimensions of closed region A’B’C’D’ as argument and produces s2 as minimal path , see Pic 10.

Since G and G1 both follows same steps as they are the same generic algorithm and they take same argument so they should produce same path as optimal path for the both regions, but it is impossible since the position of the start point with respect to the two regions ABCD and A’B’C’D’ are different, so the optimal path should also be different which leads to a contradiction. So it’s not possible to have any specific straight line, which proves that any minimal path is not possible.

Does there really exist any generic algorithm for Bellman’s lost in Forest problem?

Now if we come to the question, does there really exist any generic algorithm for Bellman’s lost in Forest problem, then in view of Theorem1, it’s clear that there does not exist any generic algorithm which produces the minimal escape path in Euclidean plane.

References

1. Bellman R. Minimization problem, Research problems. Bull of the Ameri Math Society. 1956; 62(3): 270.
2. Finch SR, Wetzel JE. Lost in a forest. American Math Month. (2004); 11: 645-654.
3. Ward John W. Exploring the Bellman Forest Problem. Retrieved 2020-12- 14.