Mathematica Eterna
Open Access

Large Time Behavior of Multi-Dimensional Unipolar Hydrodynamic Model of Semiconductor

Yanqiu Cheng^* and Ran Guo ^*Correspondence: Yanqiu Cheng, Department of Mathematics, Shandong Normal University, Jinan, 250014, China, Email: ,

Author info »

Introduction

In this paper, we consider the following unipolar hydrodynamic model of semiconductor:

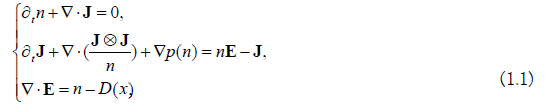
Where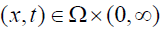

with being a bounded open set in 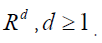The unknowns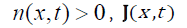represent the scaled partial density and current density of the electrons. The unknown function E denotes the electric field, which is generated by the Coulomb force of particles. If we introduce the electrostatic potential φ then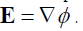 In this paper, we consider the isothermal case 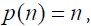which is of importance in industry. The symbols 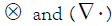denote the Kronecker tensor product and the divergence in. Is the doping profile, which means the density of impurities in semiconductor materials? We suppose.

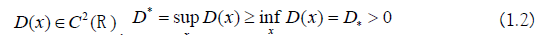
In this paper, we consider problem (1.1) with the initial conditions

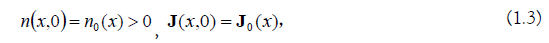
And the following insulating boundary conditions

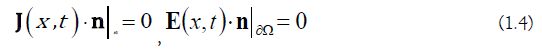
Where n is the outer unit normal vector on ∂Ω.

Now let’s recall some known results for the model (1.1). The existence and uniqueness of the subsonic steady solutions was first established by Degond- Markowich, Gamba investigated the stationary transonic solutions [1-5]. For the time dependent model, Hsiao-Yang, Luo-Natalini-Xin and Guo-Strauss proved the existence of global smooth solutions near a given steady state for different kinds of initial or initial-boundary conditions [6-14]. However, Chen proved the existence of the local generalized solutions and gave the blow up phenomenon of this equation [3]. Therefore, it is necessary to study weak solutions. The existence result of weak solutions was given in [7,15-26]. Huang and Yu proved the weak solutions converge to the stationary solutions exponentially in time when space dimension [9,25]. For more results about the unipolar model of semiconductor, we can refer to [1,8,10-12,14,16-20].

In this paper, our main goal is to prove the exponential convergence of multi-dimensional unipolar hydrodynamic model of semiconductor with insulating boundary conditions and nonzero doping profile. That is, all weak entropy solutions of problem (1.1) (1.3) (1.4) converge to the corresponding stationary system.

With an exponential decay rate, when d =1,2, he existence to smooth solution of problem (1.5) can be proved by variation method [6].

Before stating the main result, we first give the definition of weak entropy solution and some common notations.

Definition 1.1. A For everyT > 0 , the function (n,J,E)(x,t)∈(L2 (Ω×[0,T)))2d +1 is said to be a L² weak solution of problem (1.1)(1.3)(1.4) if,

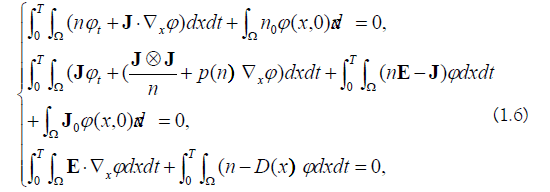
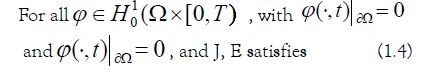
In the sense of trace. Furthermore, a weak solution of system (1.1) (1.3) (1.4) is called an entropy solution if the following entropy solution if the following entropy inequality.

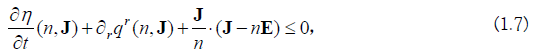
Hold in the distributional sense, where (1.7) use the Einstein’s summation symbols (η, q) , is entropy flux pair satisfying.

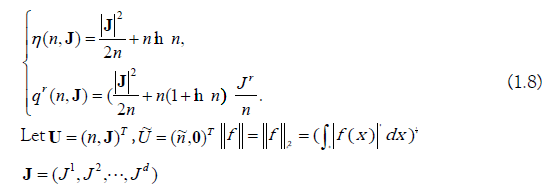
and we choose to represent different positive constants in different places.

The main result of this paper is given below.

Theorem 1.1. Suppose 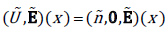is a smooth solution of problem (1.5), 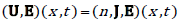is any 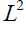weak entropy solution of problem (1.1)(1.3)(1.4). If there exist positive constants 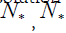and ~( ) *, * N ≤ n x ≤ Nsuch that,

For any 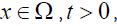then

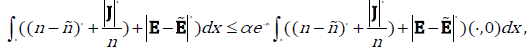
Holds for some positive constants α and β .

The Proof of Theorem

From equations (1.1) and (1.5), we obtain the following system.

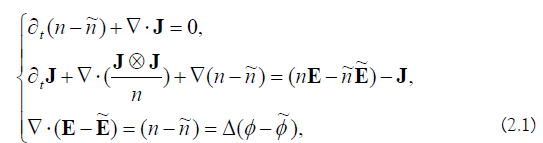
Satisfies in the sense of Definition 1.1.

The proof of Theorem 1.1 is completed in the following two theorem.

Theorem 2.1. Suppose (U,E)( x,t)

be a weak entropy solution of (1.1)(1.3)(1.4) in the time interval is a smooth solution of problem (1.5), If (1.9) and (1.10) satisfy for any and t > 0 , then,

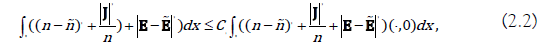
Holds for some positive constants C1

Proof: Using Einstein’s summation convention, we can rewrite the first d +1

equations of (1.1) as a hyperbolic system of conservation laws.

Where,

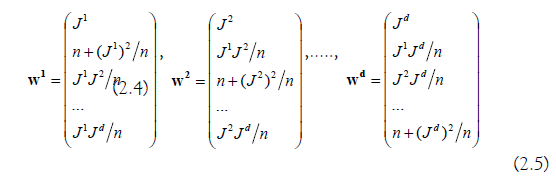
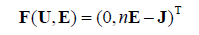
From (1,7), we obtain

With the energy production

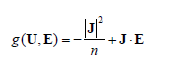
Let,

Where,

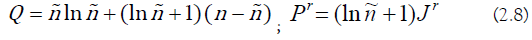
From(1.5) and (2.6) - (2.8), we obtain

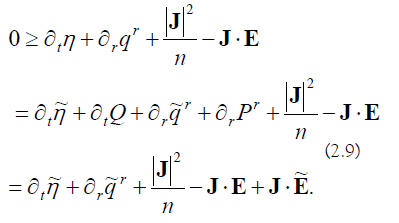
Integrating the last equation in (2.9) over Ω and using the boundary condition (1.4), we get

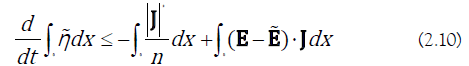
On the other hand, after integrating by parts and using the boundary condition (1.4) for several times, we obtain

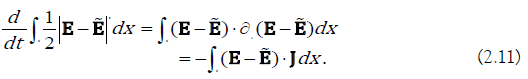
Combining (2.10) with (2.11), we obtain

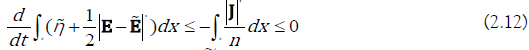
Moreover, we notice that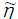

is the quadratic remainder of the Taylor expansion of the convex function n lnn around 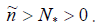. Therefore, using (1.9) and (1.10), we obtain there exist positive constants C₂ and C₃ such that,

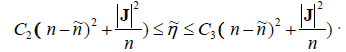
We finish the proof of Theorem 2.1.

Theorem 2.2. Under the same assumptions as in Theorem 2.1, we further have the exponential decay rate, that is,

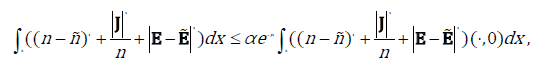
For some positive constants α and β .

Proof: To get the exponential decay rate, we would like to use the Gronwall inequality. To do this we define,

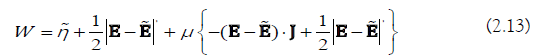
Where μ

is a real number which will be determined later? In terms of (2.1)₂ and the boundary condition (1.4), we get,

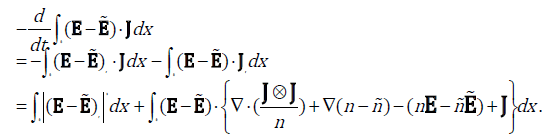
We calculate the right side of (2.14) item by item. Firstly, using Young’s inequality, we have,

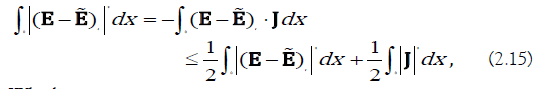
Which gives,

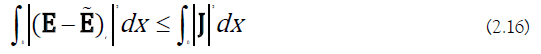
We also have,

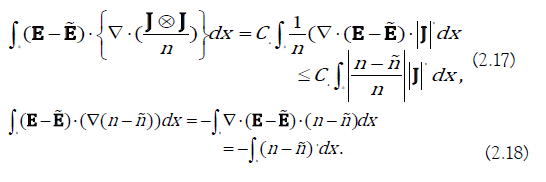
Notice

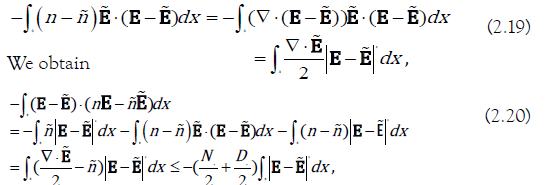
Where we have used (1.5)₂ and the fact that

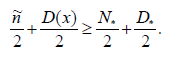
From the above analysis (2.14)-(2.20) and (2.11) (2.12), we deduce

Which

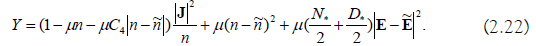
As the proof in [2], we can choose μ

small enough such that W and Y are positive definite quadratic forms. So there exist positive constants K_W and K_Y such that,

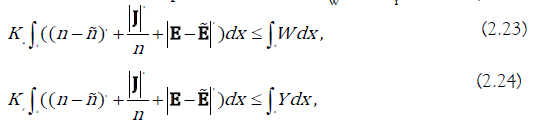
The estimate (2.21) turns into

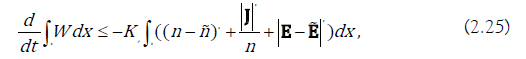
From Gronwall inequality we get Theorem 2.2, with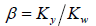

By Theorem 2.2 we can easily deduce Theorem 1.1.

References

1. Ali G. Global existence of smooth solutions of the N-dimensional Euler-Poisson model, SIAM J Math Anal. 2006;35(2):389-422.
2. Ali G, Jungel A. Global smooth solutions to the multi-dimensional hydrodynamic model for two-carrier plasmas. J Differential Equations. 2003;190(2):663-685.
3. Chen G, Wang D. Formation of singularities in compressible Euler-Poisson fluids with heat diffusion and damping relaxation, J Differential Equations. 1998;144(1):44-65.
4. Degond P, Markowich P. On a one-dimensional steady-state hydrodynamic model for semiconductors, Appl Math Lett. 1990;3(3):25-29.
5. Gamaba I. Stationary transonic solutions of a one-dimensional hydrodynamic model for semiconductors. Comm Partial Differential Equations. 1992;17(3):553-577.
6. Guo Y, Strauss W. Stability of semiconductor states with insulating and contact boundary conditions. Arch Ration Mech Anal. 2006;179(1):1-30.
7. Huang F, Li T, Yu H. Weak solutions to isothermal hydrodynamic model for semiconductor devices. J Differential Equations. 2009;247(11):3070- 3099.
8. Huang F, Mei M, Wang Y, Yu H. Asymptotic convergence to stationary waves for unipolar hydrodynamic model of semiconductors. SIAM J Math Anal. 2011;43(1):411-429.
9. Huang F, Pan R, Yu H. Large time behavior of Euler-Poisson system for semiconductor. Sci China Series A. 2008;51(5):965-972.
10. Huang F, Mei M, Wang Y, Yu H. Asymptotic convergence to planar stationary waves for multi-dimensional unipolar hydrodynamic model of semiconductors. J Differential Equations. 2011;251(4):1305-1331.
11. Hsiao L, Markowich PA, Wang S. The asymptotic behavior of global smooth solutions of the multidimensional isentropic hydrodynamic model for semiconductors. J Differential Equations. 2003;192(1):111-133.
12. Hsiao L, Wang S. The asymptotic behavior of global smooth solutions to the hydrodynamic model with spherical symmetry. Nonlinear Anal. 2003;52(3):827-850.
13. Hsiao L, Yang T. Asymptotics of initial boundary value problems for hydrodynamic and drift diffusion models for semiconductors, J. Differential Equations. 2001;170(2):472-493.
14. Jungel A, Peng Y. Zero-relaxation-time limits in the hydrodynamic equations for plasmas revisited. Z Angew Math Phys. 2000;51(3):385-396.
15. Li T. Convergence of the Lax–Friedrichs scheme for isothermal gas dynamics with semiconductor devices. Z Angew Math Phys. 2005;57(1):12-32.
16. Li H, Markowich P. A review of hydrodynamic models for semiconductor asymptotic behavior. Bol Soc Brasil Math. 2001;32(3):1-22.
17. Li H, Markowich P, Mei M. Asymptotic behavior of solutions of the hydrodynamic model of semiconductors. Proc Roy Soc Edinburgh Sect A. 2002;132(2):359-378.
18. Li H, Markowich P, Mei M. Asymptotic behavior of subsonic shock solutions of the isentropic Euler-Poisson equations. Quart Appl Math. 2002;60(4):773-796.
19. Li Y. Global existence and asymptotic behavior for a multidimensional nonisentropic hydrodynamic semiconductor model with the heat source. J Differential Equations. 2006;225:134-167.
20. Li Y. Diffusion relaxation limit of a nonisentropic hydrodynamic model for semiconductors. Math Methods App Sci. 2007;30:2247-2261.
21. Luo T, Natalini R, Xin Z. Large-time behavior of the solutions to a hydrodynamic model for semiconductors. SIAM J Appl Math. 2009;59(3):810-830.
22. Li J, Yu H. Large time behavior of solutions to a bipolar hydrodynamic model with big data and vacuum. Nonlinear Anal. 2017;34:446-458.
23. Marcati P, Natalini R. Weak solutions to a hydrodynamic model for semiconductors: the Cauchy problem. Proc Roy Soc Edinburgh. 1995;125:115-131.
24. Marcati P, Natalini R. Weak solutions to a hydrodynamic model for semiconductors and relaxation to the drift-diffusion equation. J Arch Rational Mech Anal. 1995;129(2):129-145.
25. Yu H. Large time behavior of entropy solutions to a unipolar hydrodynamic model of semiconductors, Commun Math Sci. 2016;14:69-82.
26. Zhang B. Convergence of the Godunov scheme for a simplified one- dimensional hydrodynamic model for semiconductor devices. Commun Math Phys. 1993;157(1):1-22.