Mathematica Eterna
Open Access

Multilevel Monte Carlo Techniques for High-Dimensional Problems

Fareed Rafi^{* *}Correspondence: Fareed Rafi, Department of Mathematics, Sharif University of Technology, Tehran, Iran, Email:

Author info »

Description

Monte Carlo methods have long been a fundamental of numerical simulation providing powerful tools for estimating complex integrals and solving Stochastic Differential Equations (SDEs). However, traditional Monte Carlo approaches can be computationally expensive particularly in high-dimensional settings where the number of samples required grows exponentially. Multilevel Monte Carlo (MLMC) methods emerge as a sophisticated alternative offering a way to reduce computational costs while maintaining accuracy.

Theoretical foundations of MLMC

MLMC is a powerful computational technique developed to improve the efficiency of standard Monte Carlo methods particularly in the context of numerical simulations of SDEs.

Basic concept: MLMC methods utilize a hierarchy of discretizations or approximations of a stochastic problem allowing for variance reduction by combining results from different levels. The key idea is to perform simulations at various levels of accuracy where each subsequent level requires fewer samples due to its coarser representation of the underlying process.

Hierarchical structure: Let L denote the highest level of discretization with L levels indexed from 0 (the coarsest) to L (the finest). Each level l approximates the quantity of interest Y with an associated error that decreases as increases: YL≈YL−1+ΔYL−1

Where ΔYl is the correction term representing the difference in estimates between levels l and l−1.

Variance reduction: The multilevel approach effectively reduces variance by leveraging the correlation between estimates at different levels. By estimating the total quantity Y as:

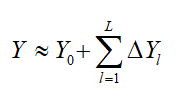
It can significantly improve convergence rates compared to traditional Monte Carlo methods. The total computational cost is then governed by the number of samples used at each level allowing for an efficient balance between accuracy and computational effort.

Advantages of MLMC

Here are some of the key benefits.

Cost efficiency: The most significant advantage of MLMC is its ability to achieve a desired accuracy with a lower computational cost compared to standard Monte Carlo methods. The hierarchical structure allows for targeted refinement where it is most needed minimizing unnecessary computations at higher levels.

Improved convergence rates: MLMC methods exhibit faster convergence rates due to their variance reduction properties. While standard Monte Carlo methods typically converge at a rate of O(N^-1/2) where N is the number of samples MLMC can achieve convergence rates closer to O(N^-1) under certain conditions significantly enhancing efficiency.

Flexibility across applications: The framework of MLMC is adaptable to various fields including finance, engineering and computational physics. Its versatility allows it to be applied to a wide range of stochastic problems making it a valuable tool in both theoretical and applied settings.

Applications of MLMC

Here are some prominent applications.

Financial mathematics: In quantitative finance MLMC methods are employed for pricing complex derivatives and assessing risk. By using MLMC to estimate the expected payoff of an option practitioners can achieve accurate results with fewer simulations enabling faster and more cost-effective risk assessments. For example: Pricing Asian options which depend on the average price of an underlying asset can be efficiently handled with MLMC techniques leading to significant reductions in computational expense.

Computational physics: In physics MLMC methods can be applied to simulate systems governed by stochastic differential equations enabling accurate predictions of physical behavior in complex systems. For example: In simulating molecular dynamics MLMC can help model particle interactions with high accuracy while minimizing the computational burden.

Engineering design: In engineering MLMC is used for reliability analysis and design optimization where uncertainties in parameters can significantly affect performance. By employing MLMC engineers can conduct robust simulations that account for variability without incurring excessive computational costs. For example: In structural reliability assessments MLMC can efficiently estimate failure probabilities aiding in the design of safer structures.

Climate modelling: Climate models often involve uncertainty in parameters and complex interactions. MLMC methods can improve the efficiency of simulations in climate modelling enabling better predictions with less computational effort. For example: Estimating the impact of climate change on sea-level rise can be efficiently analysed using MLMC facilitating timely and informed decision-making.

While MLMC methods offer significant advantages they also present challenges. Implementing MLMC requires careful consideration of the level hierarchy and the trade-offs between accuracy and computational cost. Additionally, the choice of appropriate stopping criteria and sample allocation across levels can impact performance.

Future research may focus on developing adaptive MLMC algorithms that automatically adjust sampling strategies based on real-time data or problem characteristics. Advances in parallel computing and machine learning techniques may also enhance the efficiency and applicability of MLMC across increasingly complex problems.

MLMC methods represent a powerful evolution in the field of numerical simulation providing a framework that combines efficiency and accuracy in estimating complex integrals and solving stochastic problems. By leveraging the hierarchical structure and variance reduction properties of MLMC practitioners can achieve significant improvements in computational performance across various applications.