Mathematica Eterna
Open Access
ISSN: 1314-3344
ISSN: 1314-3344
Research - (2021)Volume 11, Issue 3
In this paper we have made an attempt to establish a triple integral relation between weyl type three dimensional Saigo-Maeda operator of fractional integration and the three dimensional H-transform. Some special cases have also been established.
Laplace transform, generalized fractional integral operator, H-transform, Appell function F3.MSC2010: 26A33, 33C65, 44A10.
Saxena, Gupta and Kumbhat [16] studied two dimensional
Weyl fractional calculus. Nishimoto and Saxena [8] gave the
generalization of results given by Arora, Raina and Koul [1],
Saxena, Gupta and Kumbhat [16], and Raina and Kiryakova
[12] by proving the theorems associated with two dimensional
G-transforms. Saxena, Ram and Goree [14] proved a theorem on
two dimensional generalized H-transforms involving Weyl type two
dimensional Saigo operators. Saxena, Ram and Suthar [13] studied
the generalized fractional integration operators associated with the
Appell Function F3 as kernel, introduced recently by Saigo and
Maeda [10]. Chaurasia and Srivastava [19] established a theorem on
two dimensional 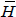 -transforms involving polynomials of general
class with Weyl type two dimensional Saigo operators. Chaurasia
and Jain [18] evaluated certain triple integral relations, and derived
a theorem on three dimensional
-transforms involving polynomials of general
class with Weyl type two dimensional Saigo operators. Chaurasia
and Jain [18] evaluated certain triple integral relations, and derived
a theorem on three dimensional 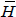 -transforms associated with the
three dimensional Saigo operators of Weyl type.
-transforms associated with the
three dimensional Saigo operators of Weyl type.
In this paper we drive a relationship between H-transforms and the Saigo-Maeda operators of Weyl type of three dimensions. The results obtained here provide extension of Saigo results, Saxena and Ram [9], Saxena and Ram [12] and Chaurasia and Jain [18].
DEFINITIONS: The Fox’s H-function [2, 3, 4] is in the form of Mellin-Barnes type [7] integral in following way
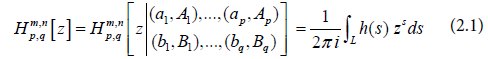
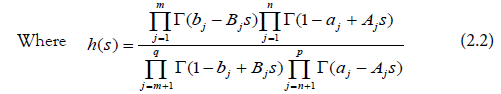
Where 0 ≤ n ≤ p, 0 ≤ m ≤ q are non-negative integers; Aj and Bj are positive; aj ( j=1,…,p) and bj (j=1,…, q) are real or complex, such that Aj ( bh + ν ) ≠ Bh ( aj λ – 1 ), ( ν, λ = 0,1, … ; h = 1,2, … , m; j = 1,2, …, n), L is a suitable contour separating the simple poles of integrand h(s) in (2.2).
Now we define generalized fractional calculus operators as follows:
Let 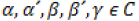 and x > 0 then the fractional calculus
operators in generalized form of arbitrary order involving Appell
function F3, due to Saigo and Maeda [10] in the kernel are defined
by the following equations:
and x > 0 then the fractional calculus
operators in generalized form of arbitrary order involving Appell
function F3, due to Saigo and Maeda [10] in the kernel are defined
by the following equations:
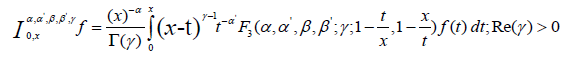 (2.3)
(2.3)
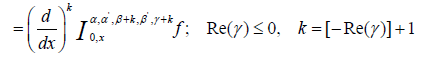 (2.4)
(2.4)
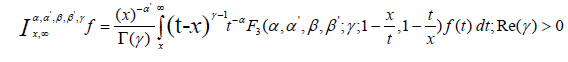 (2.5)
(2.5)
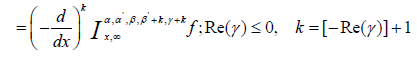 (2.6)
(2.6)
The Saigo-Maeda operators are extensions of the Saigo operators defined as follows:
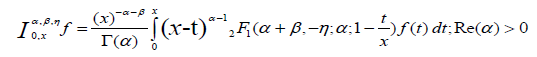 (2.7)
(2.7)
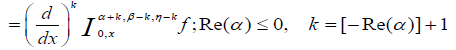 (2.8)
(2.8)
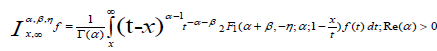 (2.9)
(2.9)
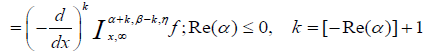 (2.10)
(2.10)
Following Chaurasia and Jain [18] we denote by u1 the class of functions f(x) on R+ which are infinitely partialy differentiable with any order behaving as O(| x |−ξ ) when x → ∞ for all ξ. Similarly by u2, we denote the class of functions f(x,y) on the R+ * R+, which are infinitely partialy differentiable with any order behaving as O(| x |−ξ1 | y |−ξ2 ) when x → ∞, y → ∞ for all ξi ( i = 1,2 ).
On the same lines we denote by u3, the class of functions f(x,y,z) defined on the R+ * R+ * R+, which are infinitely partialy differentiable with any order behaving as O(| x |−ξ1 | y |−ξ2 | z |−ξ3 ) when x → ∞, y → ∞, z → ∞ for all ξi ( i = 1,2,3 ).
The Saigo-Maeda operator of Weyl type three dimensional fractional integration of order Re(αi) > 0, Re(γi) > 0 ( i = 1,2,3) is defined in the class u3 by
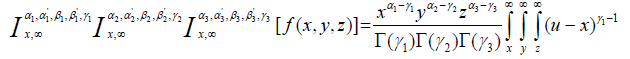

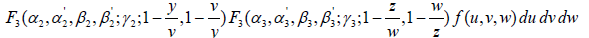 (2.11)
(2.11)
THREE DIMENSIONAL LAPLACE TRANSFORM AND
H-TRANSFORM: The Laplace transform h(p,q,r) of a function
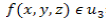 is written as [13] : let Re( p) > 0, Re(q) > 0, Re(r ) > 0
is written as [13] : let Re( p) > 0, Re(q) > 0, Re(r ) > 0
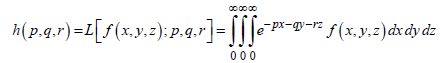 (3.1)
(3.1)
Similarly, the Laplace transform of
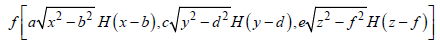
is defined by F(x,y,z), H(t) denotes Heaviside’s unit step function.
By the three dimensional H-transform ϕ ( p,q,r) of a function F(x,y,z), we mean the following repeated integral involving three different H-functions:
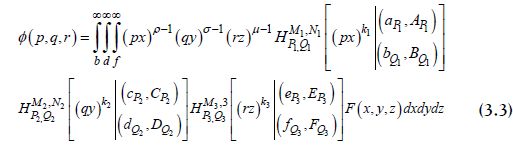
Here we assume that b > 0,d > 0, f > 0,k1 > 0,k2 > 0,k3 > 0; ϕ ( p,q,r) exists and belongs to u3. The generality of the H-function, the equation (3.3) provides a generalization of a number of integral transforms like the three-dimensional Laplace, Stieltjes, Hankel, Whittaker and G-transforms.
RELATION BETWEEN THREE-DIMENSIONAL H-TRANSFORMS IN TERMS OF THREE-DIMENSIONAL SAIGO-MAEDA OPERATORS OF WEYL TYPE
In this section we evaluate three-dimensional H-transform ϕ1( p,q,r) of F(x,y,z) which will be needed for proof of the theorem considered in this section. We have
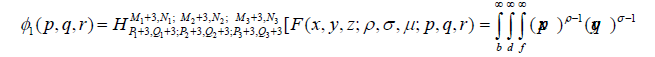
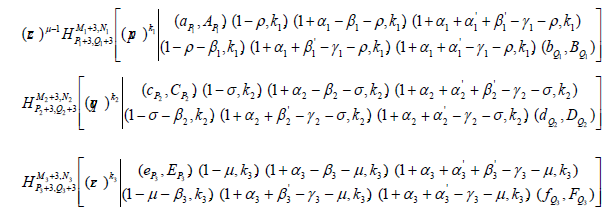
.F(x, y, z)dx dy dz (4.1)
Where it is assumed that ϕ1( p,q,r) exists and belongs to u3, the parameters k1 > 0, k2 > 0, k3 > 0 and other conditions on the additional parameters α1,α'1, β1, β'1,γ 1,α2,α'2, β2, β2,γ'2α3,α'3, β3, β'3,γ 3, corresponding to those integral involved exists.
Theorem 4.1: Let ϕ ( p,q,r) be given by (3.3) then for Re(γ 1) > 0, Re(γ 2 ) > 0,Re(γ 3 ) > 0, d > 0, d > 0, f > 0, k1 > 0, k2 > 0, k3 > 0 there holds the formula
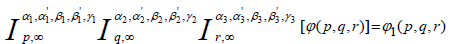 (4.2)
(4.2)
Where ϕ1( p,q,r) is given by (4.1).
Proof: Let Re(γ 1) > 0, Re(γ 2 ) > 0,Re(γ 3 ) > 0, then in view of (3.3), we find that
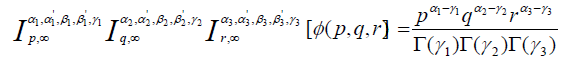
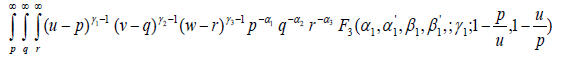
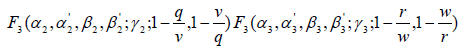
ϕ (u,v,w)du dv dw
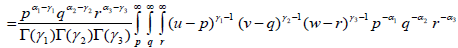
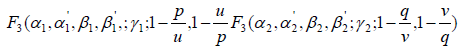
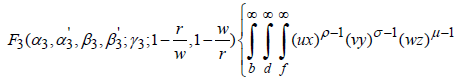
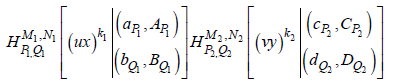

On interchanging the order of integration and evaluating the u, v, w-integrals, we get
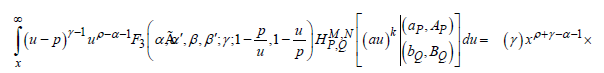
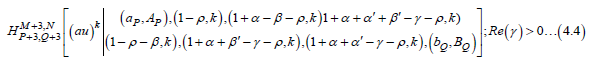
Equation (4.4) can be established by means of the following formula [18]
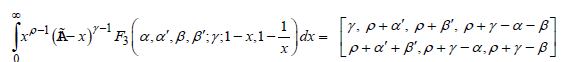 (4.5)
(4.5)
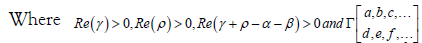 represents
the ratio of the product of several gamma functions i.e.
represents
the ratio of the product of several gamma functions i.e.
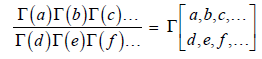
The left hand side of (4.3) becomes
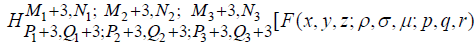
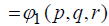
Which is required right hand side of the equation (4.2).
As far as the three-dimensional Weyl type Saigo-Maeda operators 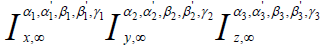 preserve the class u3, it
follows that ϕ1 ( p,q,r) also belongs to u3.
preserve the class u3, it
follows that ϕ1 ( p,q,r) also belongs to u3.
SPECIAL CASES: By putting α'1 =α'2 =α'3 = 0 , in theorem 4.1
and use the identity 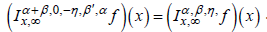 Theorem
reduced in to the form of two dimensional and one dimensional
analogue.
Theorem
reduced in to the form of two dimensional and one dimensional
analogue.
The authers are thanksful to the referee for the exhaustive comments for the improvement of the paper.
Citation: Singh, D & Jain, R (2021). On Three-Dimensional Saigo-Maeda Operator of Weyl Type with Three-Dimensional H-Tran. Mathematica Eterna 11:129. doi: 10.35248/1314-3344.21.11.129
Received: 25-Apr-2021 Accepted: 05-Jun-2021 Published: 09-Jun-2021 , DOI: 10.35248/1314-3344.21.11.129
Copyright: © 2021. Singh, D & Jain, R This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original work is properly cited.