Mathematica Eterna
Open Access
ISSN: 1314-3344
ISSN: 1314-3344
Research Article - (2020)Volume 10, Issue 1
In this paper we present some Hermite-Hadamard and Fejér types inequalities as counterpart of the developed for functions. We generalize results given for $m$-convex functions in Bracamontes, Giménez, Merentes, & Vivas, 2016, Dragomir & Toader, Some inequalities for m-convex functions, 1993 and Özdemir, Avci, & Set, 2010 among them, right-hand side of Hermite-Hadamard type and Fejér type inequalities.
Convex; m-convex stochastic processes; Fejér type inequality; Hermite-Hadamard type inequality; Convex analysis
Many inequalities have been established for convex functions and one of most famous is the Hermite-Hadamard inequality, due to the rich geometrical significance and applications see Fejér (1906), Niculescu & Persson (2006).
In 1980, K. Nikodem Nikodem, stated the line of investigation on stochastic convexity and later, several types of stochastic process have been studied based in the classical convex notions for functions, Barráez, González, Merentes, & Moros, (2015) Hudzik & Maligranda, (1994) Kotrys, Remarks on strongly convex stochastic processes, (2012) Kotrys, (2012), Kotrys, (2014), Kotrys, (2015), Maksa & Palés, (2011), Matkowski & Swiatkowski, (1993).
Gh. Toader in (Toader, 1984), introduced the concept of m-convex functions as the solutions of the functional inequality:
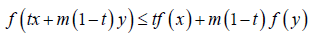
Where f:[0,1]→R and m∈[0,1] is given.
In 1993, S. S. Dragomir and Gh. Toader Dragomir & Toader, Some inequalities for m-convex functions, 1993 demonstrated inequalities of Jensen type and the Hermite-Hadamard type for these functions.
Some interesting and important inequalities for m-convex functions were developed by M.K. Bakula et al. Bakula, Pečarić, & Ribičić, (2006). Also, in 2010 M. E. Özdemir et al. Özdemir, Avci, & Set, 2010 gave some estimates to the right-hand of Hermite- Hadamard inequality for functions whose absolute values of second derivatives raised to positive real power are m-convex.
On the order hand, in the same year, Bo-Yan Xi et al. introduce concepts of the m-convex and (α ,m) -geometrically convex and establish some inequalities of Hermite-Hadamard type for these classes of functions. Xi, Bai & Qi, 2012.
In Venezuela, some researchers have developed numerous works on this topic. Bracamontes, Giménez, Merentes, & Vivas, 2016, Lara, Rosales, & Sánchez, New properties of m-convex functions, 2015, Lara, Merentes, Quintero, & Rosales, On approximate m-convexity of sub-homogeneous functions, 2016, Lara, Merentes, Quintero, & Rosales, Properties of Jensen m-convex functions, 2016, Lara, Merentes, Quintero, & Rosales, 2017, Lara, Quintero, & Rosales, 2017, Lara, Matkowski, Merentes, Quintero, & Wróbel, 2017, Lara, Rosales, & Sánchez, 2018, Lara, Merentes, Pales, Quintero, & Rosales, 2018, Lara, Merentes, Quintero, & Rosales, 2019.
Recently, S. Özcan in Özcan, 2019 introduced the concepts of m-convex and (α ,m) -convex stochastic process, as well as some Hermite-Hadamard type inequalities for the first derivative were established.
In this paper, some Hermite-Hadamard and Féjer type inequalities of m-convex functions for m-convex presented in Dragomir, 2002, Lara, Rosales, & Sánchez, 2015 and Özdemir, Avci, & Set, 2010 are develop.
Let (Ω, A , P) be a probability space. A function X :Ω→℠is a random variable if it is A -measurable. A function X:I×Ω→R, where I⊂R is an interval, is a stochastic process if for every t∈I the function X(t) is a random variable.
Definition 2.1. A stochastic process X:I×Ω→R is:
1) Jensen-convex if, for every a,b∈ I the following inequality is satisfied:
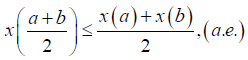 (1)
(1)
2) convex if, for every a,b∈I, t∈(0,1), the following inequality is tales place:
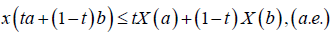 (2)
(2)
Also, we say that a stochastic process X:I×Ω→R is:
1) continuous in probability in the interval I, if for all t0∈I we have
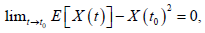
Where P − lim denotes the limit in probability.
2) Mean-square continuous in the interval I, if for all t0∈I
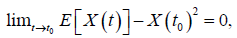
Where E [X(t)]denotes the expectation value of the random variable X(t)
3) mean-square differentiable at a point t ∈I if there is a random variable X' (t):I×Ω→R:
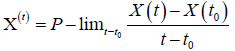
Note that mean-square continuity implies continuity in probability, but the converse is not true.
Fixed X:I×Ω→R a stochastic process with E [X(t)2 ] < ∞ for all t∈I, [a,b]⊆I, a=t_0
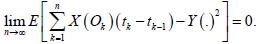
In such case, we write
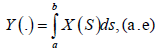
For the existence of the mean-square integral is enough to assume the mean-square continuity of the stochastic process x. Basic properties of the mean-square integral can be read in (Sobczyk, 1991).
Now, in (Özcan, 2019) was introduced the definition of m-convex stochastic process.
Definition 2.2. The mean-square stochastic process X: I×Ω→R is said to be m-convex, where m ∈ [0,1] and I=[0,c], if for every a, b∈I and t∈[0,1], we have:
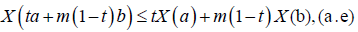 (3)
(3)
Denote by S_m (c) the class of the m-convex stochastic process on I×Ω for which X (0,∙)≤0.
Remark 2.3. From the Definition 2.2. We have the following immediate results:
i. If a, b=0 then X(0,∙)≤0
ii. For m=1, we recapture the concept of convex stochastic process (Nikodem, 1980) defined on I×Ω and for m=0, we get the concept of starshape stochastic process on I×Ω. We recall that X:I×Ω→R is starsharped if
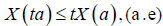 (4)
(4)
for all t∈[0,1]y a∈I.
Due to the Remark 2.3. you have the following lemma:
Lemma 2.4. If X is in the class S_m (c), them it is starshaped.
Proof. For any a∈ I. and t∈[0,1], we have:
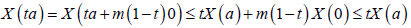 (5)
(5)
Almost everywhere.
Lemma 2.5. If X is a m-convex stochastic process and 0≤n≤m<1, then X is n- convex.
Proof. If a,b∈I and t∈[0,1], then:
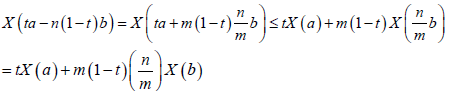
= tX(a)+m(1-t)X(b) Almost everywhere and the lemma are proved.
In order to prove the Hermite-Hadamard inequality for m-convex stochastic processes we establish the following results.
Theorem 3.1. Let X: I×Ω→R be a stochastic process non negative, m-convex mean-square integrable stochastic process, with m∈[0,1] . For every a,b∈ I , a < b the following inequality is satisfied almost everywhere:
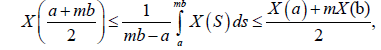 (6)
(6)
Proof. Let us calculate the right-hand side of (6). Since X is a m-convex stochastic process, we have:
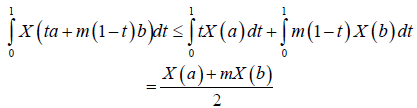
Making a change of variables= ta+m(1-t)b, in the integral:
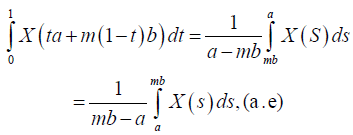
The right-hand side of inequality (6) is obtained.
On the other hand, to demostrate the left side of the inequality (6), the following transformation is performed:
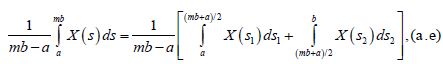
Making the change of variable 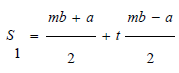 and
and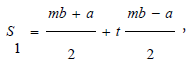 we have:
we have:
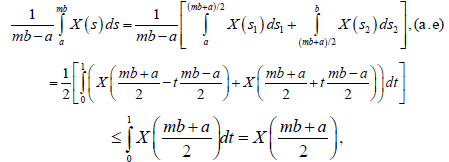
Almost everywhere. Then,
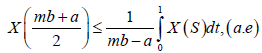
We will now point out some new results of the Hermite-Hadamard type inequalities for m-convex stochastic process. The purpose of this section is establish some new inequalities like those given in (Alomari, Darus, & Dragomir, 2009) and (Dragomir, 2002), but now for m-convex stochastic process.
Theorem 3.2. Let X: I×Ω→R be a mean-square stochastic process on I, a,b∈I with a<b and I=[0,∞). If X is m-convex stochastic process m∈(0,1] then one has the inequality:
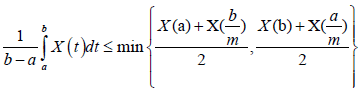 (7)
(7)
Almost everywhere.
Proof. Since X is a m-convex stochastic process:
X (ta + m(1− t )b) ≤ tX (a) + m(1− t ) X (b),(a.e)
For all, b∈ I , which gives
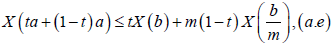
For all t ∈[0,1] . Integrating on [0,1] we obtain:
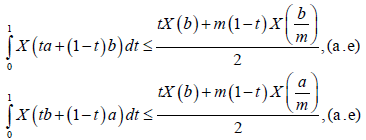
However,
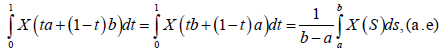
and the result is obtained.
Theorem 3.3. Let X: I×Ω→R be a mean-square stochastic process on I, a,b∈I with a<b and I=[0,∞}. If X is m-convex stochastic process m∈(0,1], then one has the inequality:
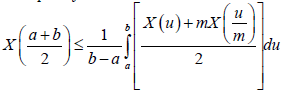
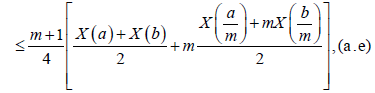
Proof. By the m-convexity of the stochastic process X, we have that
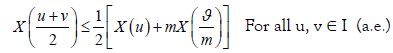
If we choose u=ta+ (1-t)b,v=(1-t) a+tb, we deduce:
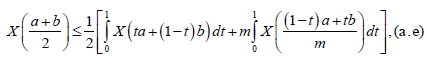
For all t∈[0,1]. Integrating over t∈[0,1], we get:
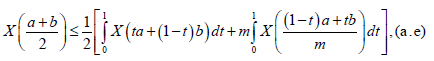
Almost everywhere for all t ∈[0,1] , Taking into account that:
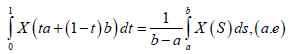
and
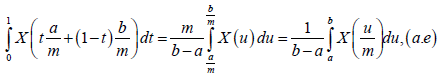
We deduce from (8) that
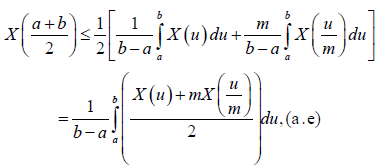
By the m-convexity of the stochastic process X, from Definition 2.2. we have the following immediate results:
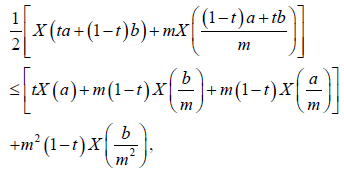 (9)
(9)
Almost everywhere, for all t∈[0,1].
Integrating (9) over t on [0,1]., we deduce:
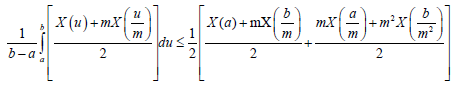
Almost everywhere. By similar argument we can state:
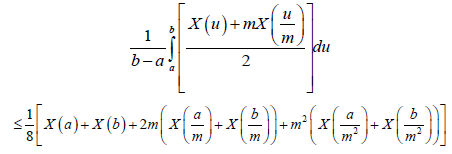
And the proof is completed.
In order to prove the following inequalities, we need lemma bellow, demostrated in (Barráez, González, Merentes, & Moros, 2015).
Lemma 3.4. Let X: I×Ω→R be a stochastic process mean-square differentiable on I, a,b∈I with a<b. If X (t) is mean-square integrable on [a,b], then the following equality holds almost everywhere:
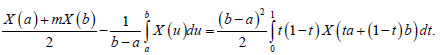
Theorem 3.5. Let X: I×Ω→R be a stochastic process mean-square differentiable on I, a,b∈I with a<b. If |X (t)|is a m-convex stochastic process, them the following inequality holds almost everywhere:
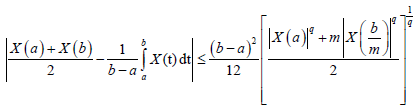
Proof. First suppose that q=1. From Lemma 3.4. we have:
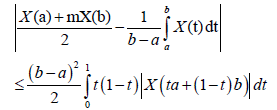 (10)
(10)
Since |X| is m -convex stochastic process we know that for any t ∈[0,1] :
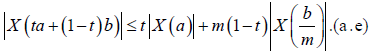
Therefore,
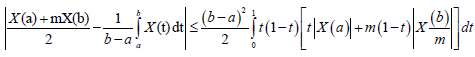
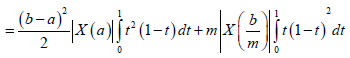
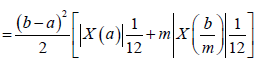
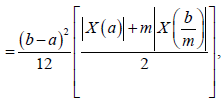
Almost everywhere, which complete the proof for this case.
Suppose now that q > 1 . Using Lemma 3.4. and the Hölder's inequality for q, p=q/(q-1), we obtain:
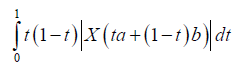
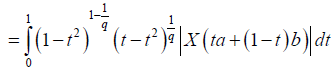
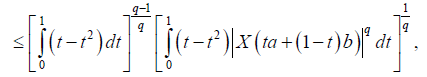
almost everywhere. Since |X'|q is m-convex stochastic process we know that for every t∈[0,1]:
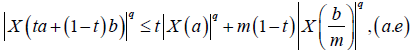
Hence, from (10) and (11) we obtain:
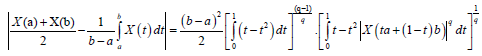
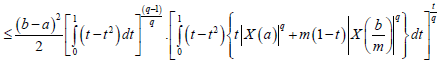
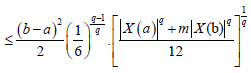
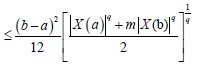
almost everywhere, which completes the proof.
Remark 3.6. If in Theorem 3.5 we choose m=1 and if |X (t,∙)|≤K on I, we obtain:
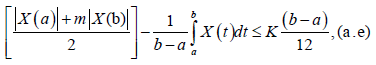
which is the right-hand side of (10).
Theorem 3.7. Let X: I ̇×Ω→R be a stochastic process meansquare differentiable on I, a,b∈I with a<b. If |X|q is a m-convex stochastic process for some fixed q>1 and m∈ (0,1], then the following inequality holds:
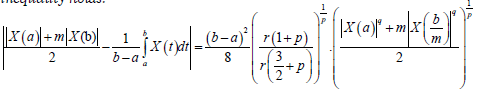
Almost everywhere, where p=q/(q-1).
Proof. From Lemma 3.4. and using the well-know Hölder's inequality we have successively almost everywhere:
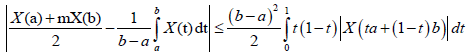
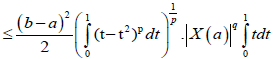
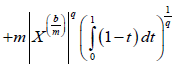
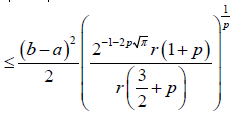
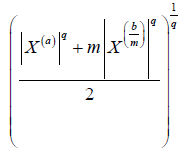
Almost everywhere, where 1/p+1/q=1. We note that, the Beta and Gamma function
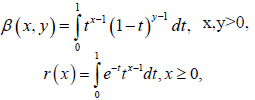
And used to evaluate the integral
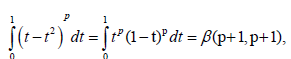
Where
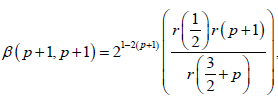
and Γ(1/2)=√π, which completes the proof.
Corollary 3.8. With the above assumptions give that |X'' (t,∙)|<K on [a,b] and 0<m≤1, we have the inequality almost everywhere:
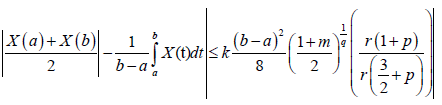
Corollary 3.9. From Theorem 3.5. and 3.7. we have the inequality for q > 1 :
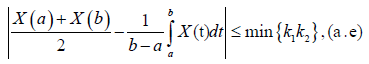
Where
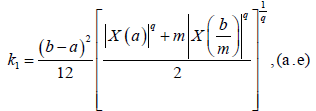
and
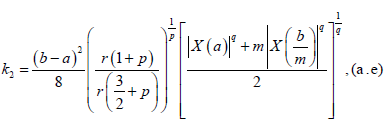
Theorem 3.10. With the assumptions of Theorem 3.7 we have the following inequality almost everywhere:
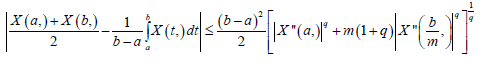
Proof. From Lemma 3.4. and Hölder inequality, we obtain:
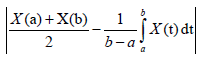
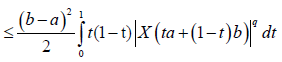
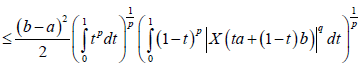
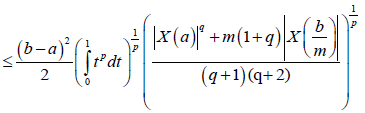
Almost everywhere. Since,
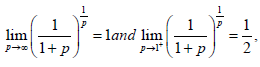
We have,
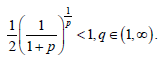
Hence, for q∈(1,∞)
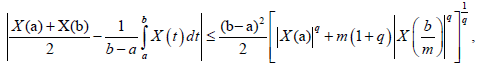
almost everywhere.
Theorem 3.11. Let X: I×Ω→R be a stochastic process mean-square differentiable On I, a, b ∈ I with a<b. If |X'|^q is a m-convex stochastic process for some fixed q>1 and m ∈(0,1], then the following inequality holds:
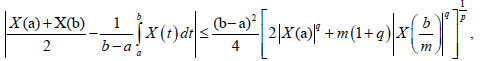
almost everywhere.
Proof. From Lemma 3.4. and the well-known power-mean inequality, we obtain:
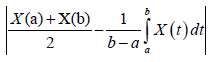
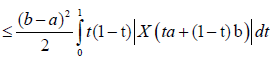
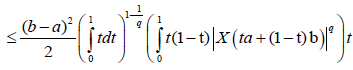
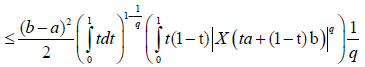
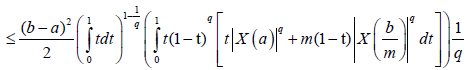
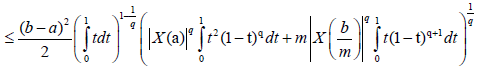
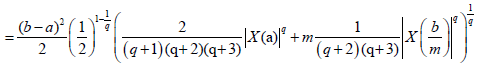
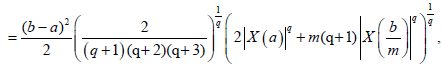
Almost everywhere.
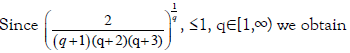
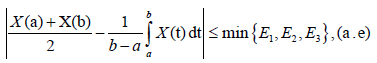
With completes the proof.
Remark 3.12. From Theorem 3.7. – 3.11., we have:
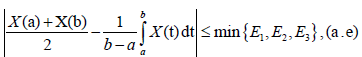
Where:
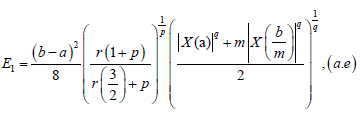
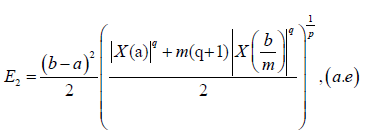
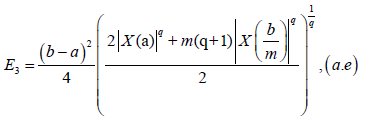
In Fejér, 1906, L. Fejér gives a generalization of (6). Now, we shall present the definition of Fejér inequality for convex stochastic processes.
Theorem 3.13. Let X : I ×Ω→ℝ be a non-negative convex mean-square integrable stochastic process. For every a,b∈ I with a < b , the following inequality is satisfied almost everywhere:
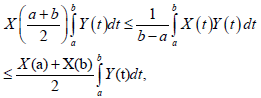 (12)
(12)
Where Y: [a,b]×Ω→R is a non-negative mean-square integrable stochastic process, symmetric with respect to (a + b) / 2 that is, Y (a + b − t,ν) = Y (t,ν) .
The following establishes some results that represent the counterpart of the results presented by M. Bracamonte et al. in (Bracamontes, Giménez, Merentes, & Vivas, 2016) for m-convex stochastic processes:
Theorem 3.14. Let X:[0,∞)×Ω→R be a m-convex mean-square integral stochastic process with m∈[0,1]. For every a,b∈I with a<b, and Y:[a,b]×Ω→R is a non-negative mean-square integrable stochastic process, symmetric with respect to (a + b) / 2 , then the following inequality is satisfied almost everywhere:
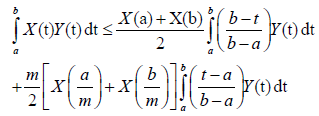 (13)
(13)
Proof. Since Y is a non negative mean-square integrable stochastic processes on [a,b]∈Ω and symmetric with respect to (a+b) ⁄2, then:
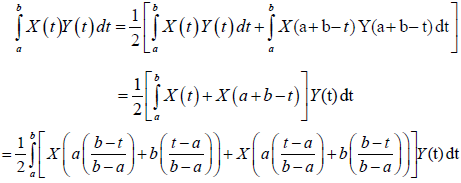
Almost everywhere. Hence, the m-convexity of X implies:
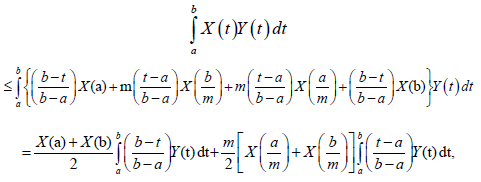
almost everywhere and the proof is complete.
Remark 3.15. Notice that if we make m=1 in (13) we get the righthand side of inequality (12) that is:
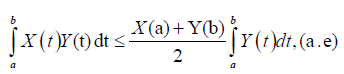
In the following, a bound is obtained for the left-hand side of inequality (12) for m-convex stochastic processes.
Theorem 3.16. Let X: [0,∞)×Ω→R be a m-convex mean-square integrable stochastic process in [a,b] with 0≤a<b and m∈(0,1). For every b∈(0,∞) 0≤a<b, and X:[a,b]×Ω→R is a non-negative mean-square integrable stochastic process, symmetric with respect to ((a+b))⁄2, then the following inequality is satisfied almost everywhere:
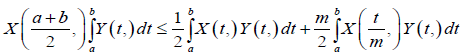
Proof. The m-convexity of the stochastic process X implies that
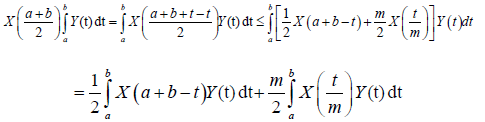
Almost everywhere. Now, X is symmetrical then:
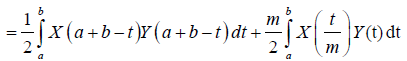
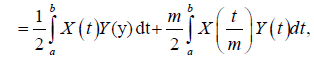
Which proves the result.
Remark 3.17. If m=1 in Theorem 3.16 we obtain:
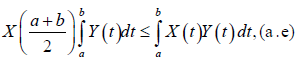
Which is the left-hand side of (12).
Now, we present a generalization of (12). First, we prove the following result:
Lemma 3.18. Let X:[0,∞)×Ω→R be a m-convex mean-square integrable stochastic process with m∈(0,1). For every ∈ [a,b]⊂[0,∞)t, there is α=α_ t∈[0,1], such that the following inequality holds almost everywhere:
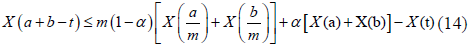
Proof. Since any t∈[a,b] can be written as t=α+(1-α)b, for some α∈[0,1] and a+b-t=a+b-αa-(1-α)b=(1-α)a+αb, we have:
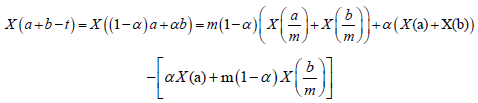
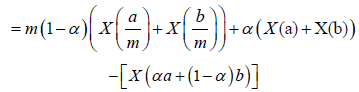
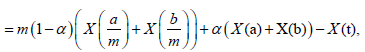
Almost everywhere.
Theorem 3.19. Under the same hypotheses of Theorem 3.14, the following inequality holds almost everywhere:
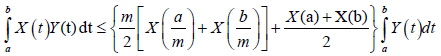
Proof. By the symmetry of Y with respect to ((a+b))⁄2 and Lemma 3.18:
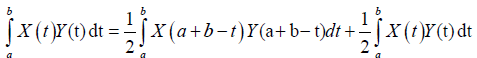
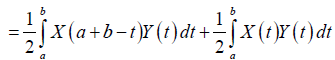
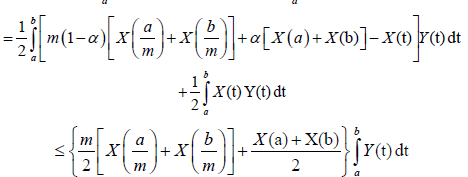
Almost everywhere.
Remark 3.20. Notice that if m=1 in Theorem 3.19, we indeed get:
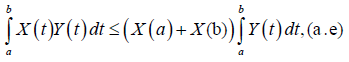
Citation: Lara T, Mejia O, Merentes N, Valera Lopez M (2020) Some inequalities for m-convex stochastic process. Mathematica Eterna. 10: 103. 10.35248/1314-3344.20.10.103.
Received: 27-Nov-2019 Accepted: 11-Feb-2020 Published: 18-Feb-2020 , DOI: 10.35248/1314-3344.20.10.103
Copyright: ©2020 Lara T, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.