Mathematica Eterna
Open Access

The Germany Problem for Beal’s Conjectıre

Ahmet F. Gocgen^{* *}Correspondence: Ahmet F. Gocgen, Department of Mathematics, Independent Researcher, Ankara, Turkey, Email:

Author info »

Description

Let, A, B, C ∈ N +; x, y, z ∈ N + > 2 . Beal’s conjecture is conjectured that: When A^x + B^y = C^z , do A, B, C have to have a common prime divisor?

Definitions and lemmas

Definition 1: According to fundamental theorem of arithmetic [1]. Composite numbers are numbers that are greater than 1 and have factors other than themselves and 1.

Definition 2: According to fundamental theorem of arithmetic [1]. Prime numbers are numbers greater than 1 that do not have any factors other than themselves and 1.

Definition 3: According to fundamental theorem of arithmetic [1]. An integer must be either a prime number or a composite number.

Lemma 1: According to Aysun and Gocgen [2]. np + p gives all composite numbers where n is a positive natural numbers and p is a prime number. Proof. np + p = p(n + 1) . Then, according to fundamental theorem of arithmetic: (n + 1 ∈ C) ⊕ (n + 1 ∈ P)

Let n + 1 ∈ C : n + 1 = pm × · · · × pm+ k

Then, p (n + 1) = p × ( pm × · · · × pm+ k )

Let n + 1 ∈ P : n + 1 = pm

Then, p (n + 1) = p × pm

Lemma 2: According to Aysun and Gocgen [2]. 2np + p gives all odd composite numbers where n is a positive natural numbers and p is an odd prime numbers.

Proof. np + p gives odd composite numbers where p is an odd number and n is an even number. Then as already proved np + p gives all composite numbers where n is a positive natural number and p is an prime number. Only possibility for odd composite just specified. Therefore, np + p gives all odd composite numbers where p is an odd number and n is an even number.

This equal to: 2np + p gives all odd composite numbers where n is a positive natural numbers and p is an odd prime numbers.

Theorems and proofs

Preliminary theorem: If A, B, C are prime and not equal to each other, then A^x + B^y = C^z equality. If so, the theory is wrong. If A, B, C are prime and equal to each other, A^x + B^y = C^z equality. If it can be satisfied or not, the theory cannot be falsified from this option. At least A, B, C values [3].

The second option, one of which is composite, is taken into consideration. There is no falsification in the second option. If it can be done, the theory is wrong. If no falsification can be made in either option, there is no alternative other than two options. Since there is and cannot be any other option, the theory is proven correct.

Preliminary proof: There are 2 basic situations.

The first case is where A, B, C are prime. Let’s start by examining this situation: s is any prime number and z; Let it be a positive natural number greater than 2. The result of sz cannot have a prime factor other than s. Based on this, we can say the following: In the expression A^x + B^y = C^z , if A, B, C are prime numbers; The prime factor of A is only A, the prime factor of B is only B, the prime factor of C is only C. Therefore, when A=B=C, A, B, C do not have a common prime factor [4].

New conjecture: Since composite numbers are numbers that can be expressed as the product of more than one prime number, the accuracy of the theory directly depends on the answer to the following question.

A, B, C ∈ P

A ≠ B ≠ C

x, y, z ∈ N + > 2 : Is A^x + B^y = C^z possible?

Well,

Where A, B, C are different prime numbers and x, y, z are positive natural numbers greater than 2:

Is A^x + B^y = C^z possible? If the answer is yes, the Beals conjecture is clearly false.

If the answer is no, the Beals conjecture is clearly correct.

Inference: Let’s start examining the question given in question 1.

The basic examination to start with will be to examine the odd/ even status of the values in the equation. So let’s start reviewing. Since there is only one even prime number, in the analysis, there can only be one even prime number, that is, no more than one of the values in the equation can be even.

Option 1: A^x =odd, B^y =odd, C^z =odd. In this case the equality would look like this: Odd+odd=odd. This option is impossible because the sum of two odd numbers cannot equal an odd number.

Option 2: A^x = odd, B^y = odd, C^z = even. In this case the equality would look like this: Odd+odd=even. This option is possible because the sum of two odd numbers will always equal an even number.

Option 3: A^x = odd, B^y = even, C^z = odd. In this case the equality would look like this: Odd+even=odd. This option is possible because the sum of an odd number and an even number always equals an odd number.

Option 4: A^x = even, B^y = odd, C^z = odd. In this case the equality would look like this: Even+odd=even. This option is possible because the sum of an even number and an odd number will always equal an odd number.

The only option that is not possible is Option 1, in which A^x and B^y and C^z are not even. However, in the possible options A^x or B^y or C^z are even [5].

Then, if the equality in question 1 can be satisfied, A or B or C=2. Let’s call this situation “love triangle for 2” or simply “love triangle”.

Then we will activate this term. Therefore, we can reduce the question to the following question:

A, B ∈ P ∩ O

A ≠ B

x, y, z ∈ N + > 2 : Is A^x + B^y = 2^z or 2^x+ A^y = B^z or A^x + 2^y = B^z possible?

Well

Can the sum of any exponent of 2 greater than two be equal to any exponent of 2 greater than two, or can the sum of any exponent of 2 greater than two and any exponent of an odd prime greater than two be equal to any exponent of 2 greater than two?

Observation: When we removed the condition that x, y, z must be greater than 2 for the equality in question 2, it was seen that x or y or z was always less than or equal to 2 in the resulting equations.

For example,

2⁴ = 3¹ + 13¹

2⁵ = 3³ + 5¹

2¹ + 3¹ = 5¹

2³ + 17¹ = 5²

A, B ∈ P ∩ O

A ≠ B

x, y, z ∈ N + :x or y or z in cases where the equations A^x + B^y = 2^z or 2^x + A^y = B^z or A^x + 2^y = B^z are satisfied Can it be proven that ≤ must be 2?

If the answer is yes, since there is a condition x, y, z>2 in question 2, equality will not be achieved and beals conjecture will be proven correct.

If the opposite is proven, the beals conjecture will be proven false, since the equality in question 2 is possible.

New observation: The expression p m can be expressed with the formulas np + p and 2np + p . Therefore, examining these statements together with these formulas may be useful to offer a new perspective.

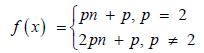
Because while the 2np + p formula produces all composite numbers, the 2np + p formula produces only single composite numbers. Since any exponent of a single prime number cannot be even, it would be inefficient and useless to examine the exponent of any odd prime through a formula that also produces even composite numbers. For this reason, the formula np+p for even primes and 2np + p for odd primes should be examined.

In the np + p and 2np + p formulas, p must be the p value in the pm expression. However, another method must be followed to determine n

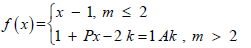
Although the above n determination method has been confirmed by experiments, it should be fully proven in another article. According to this determination:

x, y, z ≤ 2 :

2(x − 1) + 2 + 2A( y − 1) + A = 2B(z − 1) + B

or

2A(x − 1) + A + 2( y − 1) + 2 = 2B(z − 1) + B

or

2A(x − 1) + A + 2B( y − 1) + B = 2(z − 1) + 2 is happening.

sc.

2x − 2 + 2 + 2Ay − 2A + A = 2Bz − 2B + B

or

2Ax − 2A + A + 2y − 2 + 2 = 2Bz − 2B + B

or

2Ax − 2A + A + 2By − 2B + B = 2z − 2 + 2 is happening.

sc.

2x + 2Ay − A = 2Bz − B

or

2Ax − A + 2y = 2Bz − B

or

2Ax − A + 2By − B = 2z

x, y, z ≤ 2 :

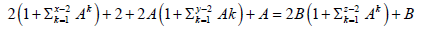
or

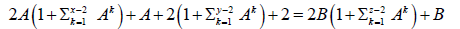
or

sc.

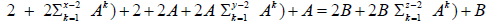
or

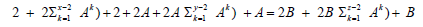
or

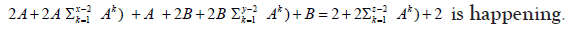
sc.

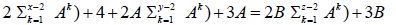
or

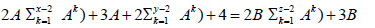
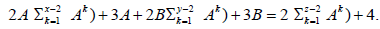
The clear difference between the two situations may affect the feasibility of the equation, but this difference could not be understood in this study and was left to another article.

The germany problem,

Lover Ex .

Ex 1.3² + 2⁴ = 5²

for z <= 2 :

z² <= 25.

Potential values for z: 2, 3, 4, 5.

for z > 2 :

z³ <= 25.

Potential values for z:2. As can be seen, the potential values found for z > 2 are values that cannot be used because they are already used in the equation. Let’s call these values lover-values. Because of the love triangle, 2 always has to be lover-value. If all potential values found for z > 2 consist of previously used values, let’s call these examples lover examples. For example, above is a lover ex. It is understood that it is [6]. Then it becomes clear why lover ex.s cannot satisfy the equation for z > 2 .

Non-lover Ex.

Ex. 1 2⁷ + 17³ = 71²

for z <= 2 :

z² <= 5041.

Potential values for z : p <= 71

for z > 2 :

z³ <= 5041.

Potential values for z: 2, 3, 5, 7, 11, 13, 17

As can be seen, all of the potential values found for z>2 are not values that cannot be used since they are already used in the equation. Let’s call these values non-lover-values. If all potential values found for z>2 do not consist of previously used values, let’s call these examples non-lover examples. The above example is a non-lover ex. It is understood that it is. In this case, it is not understood why non-lover ex. cannot satisfy the equation for z>2. Therefore, it should be explained why non-lover exes cannot satisfy the equation. With explanation and clear evidence, the beals conjecture will be solved.

References

1. Ireland K, Cuoco A. The Fundamental Theorem of Arithmetic. In Excursions in Number Theory, Algebra, and Analysis. 2023:59-88.

   [Crossref ] [Google Scholar].

2. Gocgen AF, Aysun E. A fundamental study of composite numbers as a different perspective on problems related to prime numbers. Int J Pure Appl Math Res. 2023:70-76.

   [Crossref] [Google Scholar].

3. Salem AB. A complete Proof of Beal’s Conjecture. J Eur Math Soc. 2018.

   [Crossref] [Google Scholar].

4. Ivliev YA. Solution of Beal’s Conjecture in the paradigm of quantum mathematics. Asian J Math Sci. 2018;2(1):14-18. [Google Scholar].
5. Sghiar M. The Fermat classes and the proof of Beal conjecture. IOSR J Math (IOSR-JM). 2020.

   [Google Scholar].

6. Ferreira JW. Demonstration for Fermat’s last theorem and Beal’s conjecture. Results Nonlinear Anal. 2023;6(2):130-139.

   [Google Scholar].