Journal of Theoretical & Computational Science
Open Access
ISSN: 2376-130X
ISSN: 2376-130X
Research Article - (2015) Volume 2, Issue 2
The concept of ‘Non-permissible experiments’ permeated the literature by Merzbacher as an articulation of Heisenberg’s Rules. Ample experiments in Modern Physics deem forbidden, but never the less, they do not violate the uncertainty relations. In contrast, recent ultrasonic time-of-flight experiments in condensed-matter channels, encounter violation of the uncertainty principle. Accordingly these agree with the de Broglie-Bohm interpretation of quantum mechanics, which does not support the uncertainty relations, and elaborated by the quantum theory of motion. This theory is expanded to account for ultrasound-phononic dispersion in condensed-matter channels.
<Keywords: Quantum theory of motion, De Broglie-Bohm theory, Forbidden experiments, Condensed matter, Simultaneous measurements, M?ssbauer effect, Phononic time-of-flight experiments, Harmonic-Gaussian model, Non-linear regression analysis.
A near-century-old quantum theory discord with Heisenberg’s uncertainty principle was recently rekindled by G. Bacciagaluppi and A. Valentini. Accordingly, they have translated to English the proceedings of the 5th Solvay conference, entitled “Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference” [1]. In their preface these authors scrutinize the proceedings and commentaries. But alas, they noted, the conference ended with unresolved tension between different points of views. In time this discord reduced into a debate between two groups:
• Pro: Those who agree with Heisenberg’s rules [2,3] of ‘permissible’ experiments [4].
• Con: Supporters of an alternative interpretation of quantum theory, challenging Heisenberg, and recognized as the de Broglie-Bohm theory [5-9].
Heisenberg’s uncertainty principle is discussed in his later book, Physics and philosophy, including a ‘rebuttal’ of the alternative views presented. There he also prescribes an experimental-legitimacy assertion [3].
“Therefore, the theoretical interpretation of an experiment requires three distinct steps:
(1) Translation of the initial experimental situation into a probability function,
(2) Follow up of this function in the course of time, and
(3) The statement of a new measurement to be made of the system, the result of which can then be calculated from the probability function.
For the first step, the fulfillment of the uncertainty relations is a necessary condition.”
This citation is concluded by a mandated Legitimacy Test, in the form of a ‘necessary condition’. Later authors elaborated on Heisenberg’s theory, sometimes offering additional assertions. Merzbacher’s, added a permissibility requirement: [4] “We emphasize that it is not permissible to consider φ as a measure of the relative frequency of finding various values of momentum in a large assembly of particles. Instead, φ is the attribute of a single particle.” The uncertainty principle is described above in terms of Heisenberg’s rules, [2-4] but it is also represented by the inequalities:
ΔΕ Δt ≥ ћ
ΔP Δx ≥ ћ
A strong challenge was advanced by Einstein, Podolsky and Rosen (EPR), [10] to Heisenberg’s interpretation of quantum theory, entitled: “Can Quantum-Mechanical Description of Physical Reality be considered complete?” They demonstrated that the underlying definitions of Heisenberg’s theory lead to a contradiction. However, in their concluding remarks they proposed a resolution of this paradox, arguing: “One could object to this conclusion on the grounds that our criterion of reality is not sufficiently restrictive. Indeed, one would not arrive at our conclusion if one insisted that two or more physical quantities can be considered simultaneous elements of reality only when they can be simultaneously measured or predicted.” See a thorough review of the controversy, [11] and also Cushing [12]. Leonard Schiff addresses the limits of Heisenberg’s theory [13] “the smallness of ћ makes the uncertainty principle of interest primarily in connection with systems of atomic size”. This statement sets limits, based on the smallness of ћ on both the short and long ends of atomic size. Bohm adopted EPR’s paper as the foundation of an alternative interpretation of quantum mechanics. In the first of two papers [7] he argued, on theoretical grounds, that the conventional quantum theory breaks down for distances shorter than 10-13 cm. In a following paper [8] he summarizes a proposed alternative theory (see Abstract): “in measurements we now know how to carry out, the observing apparatus disturbs the observed system in unpredictable and uncontrollable way, so that the uncertainty principle is obtained as a practical limitation on the possible precision of measurements. This limitation is not, however, intrinsic in the conceptual structure of our interpretation. We shall see, for example, that simultaneous measurement of position and momentum, having unlimited precision would in principle be possible” Hofstadter, Fechter and McIntyre reported measurements of the size of atomic nuclei, based on high-energy electron scattering experiments [14]. They recorded nuclear sizes represented by units of 10-13 cm. This compares with Bohm’s lower breakdown limit of Heisenberg’s theory for distances shorter than 10-13 cm, [7] precluding nuclear physics, based on Heisenberg/Mertsbacher’s (HM) rules, quoted above. Feynman reported on a search for an experimental violation of the uncertainty principle, focusing in the main on electrons, large atomic aggregates, and mechanical structures, such as: “a screen, an electron, a billiard ball, anything” [15] He surmised in his concluding paragraph. “The uncertainty principle ‘protects’ quantum mechanics. Heisenberg recognized that if it were possible to measure the momentum and the position simultaneously with a greater accuracy, quantum mechanics would collapse. Then he proposed that it must be impossible.” Feynman’s investigation failed, however he concluded that as long as experimental evidence is lacking: “Quantum mechanics maintains its perilous but accurate existence.”
A significant volume of experimental data, accumulated over the past century, relates to this dispute. However, in spite of a direct challenge to Heisenberg’s core permissibility rules, they did not produce evidence for a quantitative-experimental violation of the uncertainty principle. A partial summary of such experiments is provided below. These include nuclear γ−ray spectroscopy and Mossbauer spectroscopy. In contrast, recent results of phonon timeof- flight experiments [16-20] would be considered ‘forbidden’ but had produced the experimental violation both Bohm and Feynman were searching for [8,15] Such experiments would validate Holland’s quantum theory of motion, [21] which offers a comprehensive review of the de Broglie-Bohm theory. Accepting these results open a venue for extending a quantum theory to be applied to various disciplines of condensed matter, such as exemplified by the rich field of Metalurgy [22-23].
The three experimental building blocks below lie at the base of contending interpretations of quantum theory. These have been derived by averaging over a large numbers of events and or particles, irrespective of the yet unknown Heisenberg’s dictates:
1. 1900 – Planck’s Action constant h, explaining the black body electromagnetic radiation in terms of discrete quanta, containing an amount of energy defined by E = hν.
2. 1905 – Einstein, the Photoelectric Effect. The energy of a photon is given by E = hν.
The experiment consists of a monochromatic light beam, constituted of an aggregate of photons, incident on a solid surface, emitting an electron beam from the target surface. The experiment records intensity relation between the incident and emitted beams. This is implying, in addition to averaging over a large number of events, also the physics of the solid-state target. Also, Einstein: “depending on the experiment, light appears sometimes as particles and sometimes as a wave.”
3. 1924 – Louis de-Broglie – characterizes λ = h/ρ as the wavelength of a particle. This was confirmed experimentally by Davisson and Germer and independently by G.P. Thomson by observing electrondispersion by crystals. Here again, one sees a combination of the large scale averaging, and the crystalline structure of the target. When de- Broglie was asked: “Is it a particle or a wave?” He responded: “It is a particle and a wave” [9]
Note the distinction between this and Einstein’s observation above
• 1927 – The 5-th Solvay Conference – a Forum where various views of Quantum Mechanics were presented, resulting in a dispute which remains unresolved [1]. In time, the physics community divided into two factions, the majority subscribes to Heisenberg’s view while a persistent minority adopted the de Broglie-Bohm theory.
• 1924 – de-Broglie – Doctoral dissertation: Researches on the quantum theory [5]; See: Tentative d’intrpretation causale et nonlineare de la mechanique ondulatoire; Also: An Introduction to the Study of Wave Mechanics [6] These publications present an introduction to the ‘Pilot-Wave’ theory. It was also presented at the 5-th Solvay Conference. This was expounded upon by Bohm [7,8] forming what is now accepted as the ‘de Broglie-Bohm theory’ [9].
• 1926 – Schrödinger – The Schrödinger’s Equation and the associated wave functions were introduced [16]. It was also presented at the 5-th Solvay Conference.
• 1927 – Heisenberg’s ‘Uncertainty Principle’, was initially published as a paper [2]. It was also presented at the 5-th Solvay Conference. It has become known as the Copenhagen interpretation of quantum mechanics.
Nuclear-γ-ray spectroscopy
The γ-ray spectrum of an excited atomic nucleus consists of a recorded sequence of sharp spikes of γ-ray photons. Experiments producing such sequences are using special instruments enabling the study of cascading pairs of γ-rays. Of particular interest are experiments of:
• Time correlation between cascading pairs, leading to the identification and sequencing of excited, nuclear-resonance levels, from which the respective γ-rays emanate,
• Delayed-coincidence between a cascading pair of γ-ray photons, measuring the mean-life time of a resonance-energy level.
• Angular correlation between a cascading pair, providing additional structural information about the resonance-energy levels of the nuclei.
These experiments consider the γ-ray spectrum as a collection of discrete photonic beams, rather than a superposition of wave packets. Hence Heisenberg’s rules are invalidated. Furthermore, the experiments constitute of averaging a large number of events, i.e. γ-ray photons, emitted by transitions between nuclear-resonance levels. These energy levels are determined by the multi-body interaction of a large number of sub-nuclear particles. Either way they constitute violations of Merzbacher’s auxiliary rule, as outlined above.
Mössbauer-resonance spectroscopy
The Mössbauer Effect, also known as “Recoilless emission of nuclear γ-rays,” was discovered by Roudolf L. Mössbauer in 1958, while studying the nuclear-radiation fluorescence of Gamma radiation in Ir191 [24]. An early theoretical investigation by Harry J. Lipkin [25] takes note of the fact that the Mössbauer Effect is evident only for nuclei embedded in solid state samples. Hence:
“The recoil momentum is taken by the crystal as a whole, with negligible probability, although small, that there is no energy transfer to or from the lattice vibrations.”
As such it implies a violation of the HM rules. However, once the effect was also verified experimentally for Fe57, a rapid development in Mössbauer Spectrometers followed [26-30] much research was attracted, mostly by experimental physicists, chemists, and a few theoreticians. In fact, Heisenberg’s theory did not predict this effect, nor did it offer any guidance for designing and carrying out proper experiments. It was the experimental physicists who led to the development of Mössbauer Spectrometers. These devices employ acoustically modulated γ-rays, producing a 1-st order (relativistic) Doppler shift, affecting energy resolution far exceeding the line-width of the respective γ−Ray photons. Moreover, for the study of nuclear resonance levels, they offered higher accuracy employing the seminal Breit-Wigner equation,
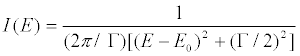 (1)
(1)
where Eo represents the centroid and Γ the full-width at half maximum (FWHM) of the intensity function I(E). The two parameters were extracted from the data simultaneously by a non-linear regression method.Equation1 is also known as the Lorentz, or Cauchy distributions. Frauenfelder [26] describes several early versions of Mössbauer Spectrometers, some were mechanically, and other where electronically driven. All employed 1-st order relativistic Doppler shift of the energy of the respective γ-ray photons, to scan the corresponding frequency distribution. He highlights the one by S. L. Ruby and D. I. Bolef, [25] employing acoustically modulated γ-rays, at play with a Multi-Channel Analyzer (MCA), to generate a simultaneous display of a full scanning range of a specific Mössbauer-resonance line, or spectra. A more advanced version was utilized [26] in a study of lattice dynamics in molecular solids. The system benefited from rapid advances in Solid- State and Digital Electronics, which facilitated digital-velocity control and a built-in thermal-drift compensation of the instrumental setup. Also included was a computer interface for a nonlinear-regression analysis of the spectra in terms of the Breit-Wigner function. A customized, commercial cryogenic system was incorporated to include programmable temperature control, allowing the planning of up to 50 temperature points, each of which relating to a distinct Mössbauer spectrum. These experiments increased accuracies in the measurement of the Mössbauer thermal shift, caused by the 2-nd order Doppler shift, enabling the observation of the effect of Zero-Point Motion (ZPM), [29] and the characterization of intra- and inter-molecular dynamics [30]. This produced higher sensitivity in measuring chemical (isomer) shifts. The higher resolution and accuracy made it possible to determine very fine physical effects on Mössbauer energy levels:
Mössbauer Fraction (f): temperature dependence of the ratio of the intensity of Mössbauer-γ-Rays emitted as recoil-less photons depends on [26,27]
Ln f=-
Line-width: allowing for precision-frequency mapping of the respective Breit-Wigner energy distribution, such studies confirm the densitydistribution- shape for the case of the Fe57 14.37 Kev γ-Ray photons, yielding the ratio:
(ΔΕ ) / Ε ∼ 3×10-13 (3)
This defines a broadened-monochromatic, energy distribution [22].
Chemical shifts (isomer shifts): small but measurable shifts of the respective nuclear-resonance levels, due to changes in the chemicalbonding environment in solid-state samples.
2nd order Doppler shift (Thermal shift): δDoppler – the temperature dependence of the thermal shift is represented by
δDoppler = - ½ (< v2 > / c2) E γ (4)
This relation uncovers dynamic parameters of Mössbauer nuclei embedded in solid-state samples [27,28].
Fine structure: nuclear energy-level splitting due to dielectric and magnetic properties of solid state samples under study.
Mössbauer’s γ-rays form a subset of nuclear γ-ray spectra. Accordingly, their study constitutes a challenge to HM mandates for acceptable experiments. Moreover, this topic displays the difficulties in forming a basic theory of quantum mechanics. In addition to the role played by relativistic-Doppler shift, it combines the interpretation of sub-nuclear effects, impact of chemical-bonding, electronic structure, interaction with lattice dynamics, and macroscopic phenomena associated with dielectric and magnetic solids. And finally, one should not lose sight of the fundamental observation that the Mössbauer effect is evident only when the nuclei are embedded in solid samples. Hence, any attempt at generalizing the basic quantum theory, has to account for the full range of experimental observations listed above. This would corroborate the EPR’s argument that the conventional quantummechanical description of physical reality must be considered incomplete [10].
Phononic dispersion in condensed matter – ultrasonic timeof- flight experiments
Recently we have produced an ultrasonic study of phononic traverse in condensed-matter-channels, challenging the universality of the uncertainty principle [17-20]. These reports include detailed descriptions of the experimental setup and methods, as well as the signal processing methodology, including a detailed discussion of the non-linear regression analysis. These experiments rest on EPR’s definition of the concept of ‘simultaneous physical measurements’, [10] and on discovery that ultrasonic phonons are accurately described by a 5-parameter harmonic-Gaussian model. These parameters are derived simultaneously from the experimental data via nonlinearregression analysis. Two of the 5 parameters, the so called ‘carrier frequency’ (ν) and ‘propagation-time’ (to), are shown to jointly produce high accuracy, far beyond the limits set by the uncertainty principle. However, such experiments entail the dynamics of large aggregates of atoms, molecules and domains, and are based on averaging over a large number of events, and thus would be rendered ‘in-permissible’ by the HM experimental-design rules. In contrast, these are in accord with the de Broglie-Bohm theory, which was the subject of a comprehensive discussion by Holland in his Quantum Theory of Motion [21]. These experiments and the associated analysis are presented in some details below. Pulsed ultrasonic transducers are used to launch oscillatory stress pulses into a condensed-matter channel and to detect returning echoes. Figure 1 displays a stress-pulse train, generated by attaching a commercial, buffered-20MHz transducer to a 4.5 mm thick crystallinesilicon plate. The observed leading pulse corresponds to a reflection from the front of the plate while the rest of the equidistant pulses entail echoes of internal reflections within the silicon plate. The monitored returning signal represents magnitude vs pulse-arrival time at the transducer/detector. The horizontal scale consists of 25000 time intervals produced by a contemporary digital scope, corresponding, in this setting, to a full horizontal scale of 10 μ-seconds. This timeresolution allows for several hundreds of data points, covering any visible Echo, sufficient for an effective nonlinear regression process, applied to each particular echo, as illustrated in Figure 2.
Figure 1: Screen copy of the data display of the ‘time of arrival’ of the various ultrasound echoes as detected by the piezoelectric transducer and recorded by the Digital Scope. The width of the two rectangular data windows: Left 1500 and right 700 data points, corresponding to the 1-st and 15-th reflections.
Figure 2: A comparative display of the 1-st and 15-th reflections analyzed using the Harmonic-Gaussian Template (HGT) as a model for a nonlinear regression process. The Gaussian envelope and the HGT curve are represented by solid lines, the experimental data represented by dashed lines, and the residual curves by dash-dot lines. The bottom signal magnified by a factor of 30 for visual comparison.
Visual inspection of Figure 1 reveals that all visible echoes display a common shape consisting of a ‘carrier frequency’ modulated by a (Gaussian) envelope. Such a wave form is represented by
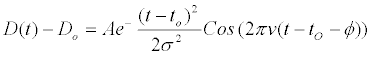 (5)
(5)
where D0 represents a baseline correction, A – magnitude factor, to – centroid arrival time, σ– a Gaussian-width parameter, ν – carrier frequency, and φ - time shift between the Gaussian centroid and cosinusoidal maximal point. The corresponding phase shift between the two forms is given by the product Φ=νφ. While D0 is determined independently, the other five parameters have been shown to vary with the changing arrival time to for the different multiple-reflection echoes [17-20].
In our earlier works we have reported results of phonon dispersion in various fluid columns and in a silicon reflector. We have also explored assorted reflectors made of steel, copper, aluminum alloys, brass, Plastic (PMMA) and soft materials. Similar observations were made for other transducers. Carrier frequencies ranging between a fraction of a MHz and up to 40 MHz were observed. In all we have found similar quality of fit by the HGT model (Equation 5). It seemed to indicate that the HGT represents an intrinsic property of the traversing stress pulses in condensed-matter channels, implying that these are manifestations of de Broglie-type particle-and-waves, i.e. acoustic phonons. Currently, description of corpuscular aspect of the phonon is associated with a Gaussian envelope, the propagation time is represented by the motion of the centroid, and the wave features, by the carrier frequency and the phase shift.
Again, (Equation 5) is referred to as the Harmonic-Gaussian Template (HGT) and it serves as a mathematical tool, part of a nonlinear-regression process, applied to the experimental data. The accuracy of the HGT representation is illustrated in Figure 2, showing the prevailing monochromatic frequency of the dominant phonon. The top signal corresponds to the leading echo reflected from the front of the silicon plate, and the bottom signal, magnified 30 folds for visual comparison, represents the 15-th echo from the back. The separation between two consecutive echoes corresponds to a traverse of twice the thickness of the reflector plate, i.e. 9 mm, as well as two additional internal reflections before returning towards the detector.
Thus, the total propagation-trajectory difference between the two selected echoes amounts to 126 mm, including 28 additional internal reflections. It is seen that the quality of the HGT representation survived the long trajectory and the multitude of internal reflections associated with the 15-th echo.
An emphasis is placed on the analysis of the experimental errors, divided into two classes:
(1) Statistical errors: Table 1 contains a detailed summary of the analysis of the experimental statistical errors as reproduced from Ref [20], where three repeated experiments were analyzed, providing estimates of the statistical errors for all 5 parameters, extracted simultaneously from the experimental data. It also includes the respective averages and standard deviations, as well as the derived estimate for Δν Δto ≡1⋅ 10 −8, which is incompatible with Heisenberg’s inequalities. Both sides of this expression ought to be multiplied by ћ to be compared with Heisenberg’s inequalities.
| A sample of derived HGT parameters1 | |||||
|---|---|---|---|---|---|
| File | Magnitude | Propagationtime(to):(sec.) | Sigma (s)(sec.) | Frequency(n) (Hz) | Time shift(sec.) |
| 40722000.csv | 0.43191 | 0.0000134116 | 3.2390E-8 | 20.9298E6 | 7.2192E-9 |
| 40722001.csv | 0.43213 | 0.0000134115 | 3.2373E-8 | 20.9295E6 | 7.2186E-9 |
| 40722002.csv | 0.43214 | 0.0000134115 | 3.2373E-8 | 20.9300E6 | 7.2261E-9 |
| Average | 0.43206 | 0.0000134115 | 3.2378E-8 | 20.9298E6 | 7.2213E-9 |
| Standard Deviation |
0.00011 | 4.471E-11(=Δto) | 8.014E-12(=Δs) | 205(=Δn) | 3.40E-12 (=Δf) |
| Δn Δto ≅205 ×4.47 ×10-11≅1×10-8 | |||||
Table 1: Data1 reproduced from Ref. [20]. The data are truncated for display purposes, however, averages and standard deviations are based on the full accuracy of the digital data.
(2) Systemic errors: Estimates of the sensitivity of the extracted parameters to the presence of acoustical noise represented by the residual curves shown in Figure 2. The results indicated similar order-of-magnitude as that of the statistical errors. Of interest are the combined accuracies of the variable pair corresponding to the frequency and to the corpuscular-propagation time, which were shown [20] to yield:
ΔΕ Δto ≅ 1⋅ 10 −8 ћ<<ћ (6)
Note the strong numerical disparity with Heisenberg’s uncertainty relations.
All the physical experiments cited above would be rendered ‘forbidden’ by HM’s mandates. Accordingly, Schiff set a limit on the validity of Heisenberg’s theory on both the short and long ends of the atomic size [13]. On the other end Bohm proposed a lower theoretical distance-validity limit of 10-13 cm. Similarly, when combined with Hofstadter’s experimental measurements of the size of atomic nuclei, also of the order of 10-13 cm, [14] exclude nuclear physics from Heisenberg’s rules. This was corroborated by Nuclear- and Mössbauerspectroscopies, discussed above. Furthermore, Lipkin’s theoretical discussion of the coupling between the dynamics of the Mössbauer nuclei and the lattice dynamics of the solid samples, in which such nuclei are embedded, constitutes an extension of the description of physical reality of the kind that the EPR paper was calling for. As such, Lipkin’s paper could have been considered as precursor to Holland’s Quantum Theory of Motion [21]. At the higher end of the atomic scale, Feynman searched for experimental evidence for such a violation, and failed, but was not convinced. In his final paragraph [15] he criticized Heisenberg on that “when he (Heisenberg) realized that if it were possible to measure the position and momentum simultaneously with a greater accuracy, quantum mechanics would collapse, and thus he asserted that such experiments should be forbidden”. The extended discussion of the Mössbauer Effect highlights an expanded range of very-low-energy physical Phenomena, the measurement of which was made possible by the discovery of this Effect, and the development of advanced Mössbauer Spectrometers. The interpretation of this range of physical observations would require the kind of modifications of the quantum mechanical wave function as are called for by the EPR paper. The phonon ‘time-of-fight’ experiments follow the line of thought of Einstein and Bohm, emphasizing the role to be played by simultaneous measurement of two (or more) associated physical variables. This provides the experimental evidence that Bohm and later Feynman were looking for. Simultaneous measurements of the experimental uncertainties were implemented for all 5 variables, characterizing the propagating phonons in condensed matter channels. This experiment would also fall into illegitimacy, but, unlike in nuclear- and Mössbauerspectroscopy cases, it did produce numerical data, in violation of the uncertainty relations, [20] with joint accuracies well below the limits prescribed by Heisenberg’s inequalities.
When a physical experiment is pronounced ‘illegitimate’, or ‘forbidden’, it implies no theoretical support for the respective discipline by the traditional quantum mechanics. The list of such unsupported fields includes all the disciplines which fall under the umbrella of physics of condensed matter. On the other end, an alternative interpretation of quantum mechanics, that does not support the Heisenberg/Merzbacher rules, offers a clearer path to the development of a universal theory. This observation applies, for example, to the de Broglie-Bohm pilotwave theory, which has Received recently considerable theoretical attention [1,31-35]. Note that the ultrasonic phonons make up a type of uncharged particles, which commands little or no interest by current followers of both versions of Quantum Mechanics. Whereas these experiments would be categorized as ‘forbidden’ by the Heisenberg’s rules, they naturally fit as an extension of the de Broglie-Bohm pilotwave theory, and thus to Holland’s quantum theory of motion.