Journal of Clinical and Experimental Ophthalmology
Open Access
ISSN: 2155-9570
ISSN: 2155-9570
Research Article - (2023)Volume 14, Issue 5
Significance: A method is needed to quickly determine the Minimum Blank Size (MBS) of spectacle lens for the chosen frame. Selecting the MBS is important in making high quality eyeglasses with appropriately thin centers and edge thicknesses, while maintaining light weight, cost effectiveness, and time efficiency. Using MBS can help make the decision whether to use an uncut lens blank from commercially available stock or to have the surfaced lens specially ordered from a lab.
Purpose: This article introduces a new chart for instantaneously, easily and accurately determining the MBS for a specific frame and will help select a suitable blank lens and therefore control the quality, cost and turnaround time of a pair of eyeglasses.
Methods: The new chart was designed with serial concentric circles matching the commonly available stock lens sizes and the surfaced lens sizes, with a series of vertical lines representing the range of inter Pupillary Distances (PD). Inside the circles, a group of horizontal lines mark vertical decentration in millimeters, while two groups of vertical lines, located above and below the horizontal lines, mark horizontal decentration. By placing the selected frame on the chart correctly, the MBS is determined immediately.
Results: This chart has been used without any special training, for determining the MBS. It can be used in any situation with or without decentration of the optical center from the patient’s visual axis. The chart has proven to be faster and more accurate than using current formula calculations.
Conclusion: Since the unfinished blank size controls the weight, thickness, and edging time of a finished pair of lenses, it is essential to determine MBS before making a pair of eyeglasses. The current method to determine the MBS, calculated by formulas using the frame measurements is tedious, time-consuming and subject to inaccuracy. This new chart is a graphically instinctive and intuitive tool that can easily be applied in clinical dispensing to meet the general and special optical requirements of the lenses in a finished pair of eyeglasses.
Refractive visual impairment; Pupillary distances; Spectacle lens; Minimum blank size
Refractive visual impairment is a global public health challenge [1-4]. Eyeglasses remain the primary means to correct vision problems resulting from refractive errors [5]. The eye care professionals' role in eye-care delivery continues to evolve. Primary eye care is defined as the provision of appropriate, accessible and affordable care that meets patients’ eye care needs in a comprehensive and competent manner [6]. This includes the responsibility to control the quality of dispensing and fabricating eyeglasses. In many areas of the world, patients get their glasses directly from their eye care professionals [7].
In those practices that control their own dispensing, producing a well-designed pair of eyeglasses depends on knowing the relationship between lenses, frames, and how stock lenses or surfaced lenses will fit into the patient’s specific frame. The final product should not only correct patient's vision problem, but also meet the patient's cosmetic and economic needs. Therefore, it is critical to select a suitable frame shape and size for their required lens power. Next, the Minimum Blank Size (MBS) should be determined, and then decide whether the uncut lens is from a stock lens blank or requires a custom surfaced lens. If uncut blank is available from commercially available stock the finishing process is more cost effective and time efficient than if a surfaced blank is required.
The effect of the uncut blank size on a finished lens is greater for plus lenses than for minus lenses. Unnecessary use of a large lens blank on a plus lens will result in longer edging time and a heavier lens with a thicker center with greater cosmetic magnification. On a minus lens, an overly large blank will not affect the center thickness or the weight of the finished lens, although the edging time will be significantly longer [8]. Therefore, determining MBS is more important for plus lenses. Presbyopia mostly needs plus lens. Presbyopia is a common, physiological age-related vision disorder and has been affecting more than one billion people globally [9-14]. Hyperopia also needs plus lens to correct its vision. Among children, the overall prevalence of moderate to high hyperopia (≥ 4.0 D) in the worse eye was 3.2% [15]. If the MBS is much smaller than the available stock lens, a surfaced lens should be ordered, especially for the children with high plus power prescription. The uncut lens size should be just large enough to fit into the chosen frame, but also be as small as possible to make a thinner center and edge thickness, and lighter weight of the finished lens.
Currently, in practice, the MBS is calculated using the following formulas [16-18].
MBS=(FCD-PD)+ED or MBS=2(decentration)+ED
Frame Center Distance (FCD) is the distance between the Geometric Centers of the Frame (GCD), often called the frame PD, which is equal to measurement A plus Distance Between the Lenses (DBL), PD is the patient inter Pupillary Distance, ED is the Effective Diameter of a lens, which is twice the distance from the geometric center of the frame to the peak of the frame bevel that is farthest from the geometric center. The decentration per lens is the distance between the geometric center of the frame and the patient pupil center or the optical center of the lens, assuming the patient pupil center coincide with the optical center of the lens, that is, equals half of the difference between the frame FCD and the patient PD.
During dispensing it is difficult to find the ED that needs to locate the geometric center and the farthest point of the frame and then calculate the MBS with the formulas.
Design of the chart
We have designed a chart, which can easily, accurately and instantly determine the MBS without the need to obtain the measurements of ED, FCD and calculating the MBS.
As shown in Figure 1, the chart has three solid concentric circles representing the three commonly available commercial stock lens diameters of 60 mm, 65 mm and 70 mm. There are also four dotted concentric circles with diameters of 40 mm, 45 mm, 50 mm and 55 mm that represent the sizes of surfaced plus lenses. The center point of these concentric circles represents the optical center of the blank lens. There are eight vertical lines representing the patients’ inter-pupillary distances PD of 40 mm, 45 mm, 50 mm, 55 mm, 60 mm, 65 mm, 70 mm and 75 mm. The long horizontal line and the shorter vertical line across the center of the concentric circles help locate the frame properly. Inside the circles, there are a group of horizontal lines, which mark vertical decentration in millimeters with a maximum of 10 mm up or down, and two groups of vertical lines, located above and below the horizontal lines, which mark horizontal decentration in millimeters with maximum of 15 mm in or out (Figure 1).
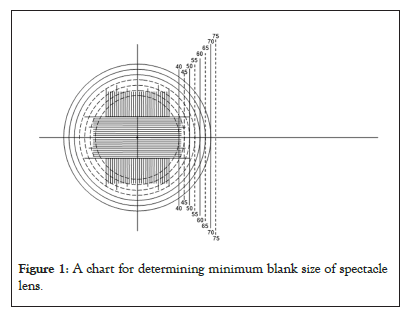
Figure 1: A chart for determining minimum blank size of spectacle lens.
Operation of the chart
General use without decentration between the optical center of the lens and the visual axis of the patient (as determined by PD): As shown in Figure 2, while keeping the datum line of the frame aligned with the long horizontal line, line up the middle point of the frame’s bridge with the long vertical line of the PD (patient PD is 60 mm). Determine the smallest circle that contains the contour of the frame (65 mm in this example). That circle, 65 mm, is the MBS (Figure 2).
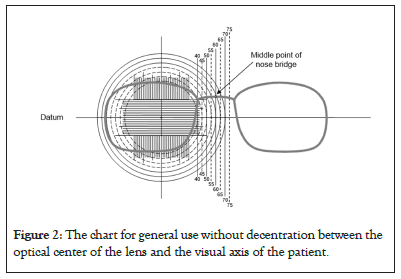
Figure 2: The chart for general use without decentration between the optical center of the lens and the visual axis of the patient.
It is recommended that monocular PD measurements be used for the prescription lens orders with aspheric and high-powered lenses. In those cases, the monocular PD (30 mm, for example) should be doubled (60 mm), then line up the middle point of the frame’s bridge with the long vertical line of PD (60 mm).
Specific use requiring decentration between the optical center of the blank lens and the visual axis of the patient: It includes
Vertical decentration: For a decentration up (5 mm for an example), line up the middle point of the frame’s bridge with the long vertical line of the PD, then vertically move the frame’s geometric center down (5 mm) while keeping the datum line parallel to the long horizontal line. Determine the smallest circle that now contains the contour of the frame. That circle is the MBS.
For a decentration down, vertically move the frame geometric center up while keeping the datum line parallel to the long horizontal line. Determine the smallest circle that now contains the contour of the frame. That circle is the MBS.
Horizontal decentration: First, line up the middle point of the frame’s bridge with the long vertical line of the PD, and then mark a vertical line on the frame’s demo lens through the shorter vertical line across the center of the concentric circles. For a decentration (10 mm for an example), horizontally move the vertical line marked on the frame’s demo lens outward (10 mm). Determine the smallest circle that now contains the contour of the frame. That circle is the MBS.
For a decentration out, horizontally move vertical line marked on the frame’s demo lens inward. Determine the smallest circle that contains the contour of the frame. That circle is the MBS.
The minimum blank size of a lens is equal to twice the minimum radius of the finished lens, which is the distance from the optical center to the farthest point along the edge of the finished lens shape. If the optical center of the lens coincides with the geometric center of the frame, the minimum blank size is equal to the effective diameter. However, the optical center often does not coincide with the geometric center of the frame. Therefore, the MBS is often larger than the effective diameter and needs special methods for determining.
In practice, formulas are currently used to determine the MBS, but they are only accurate when both the optical center and the peak of the lens bevel are located on the datum line and on the opposite sides of the geometric center of the frame. As shown in Figures 3A and 3B on left side, the frame has an oval shape with the farthest peak, P, and the optical center, O, located on the datum line, and located on the opposite sides of the geometric center of the frame, G. The MBS is equal to twice the distance from O to P. MBS=2 OP=2(GO+GP)=2(decentration)+ED. It agrees with the formulas (Figures 3A and 3B).
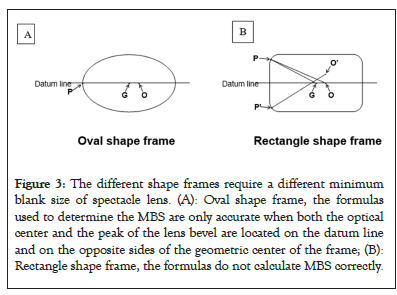
Figure 3: The different shape frames require a different minimum blank size of spectacle lens. (A): Oval shape frame, the formulas used to determine the MBS are only accurate when both the optical center and the peak of the lens bevel are located on the datum line and on the opposite sides of the geometric center of the frame; (B): Rectangle shape frame, the formulas do not calculate MBS correctly.
The formulas, however, are not accurate if P is not on the datum line, as shown in Figure 3A on right side, when the frame has rectangle shape with P not on the datum line. According to the formulas, MBS should be equal to twice (PG+OG), but the real MBS is twice OP, which is obviously smaller than the formula’s calculated value. As shown in Figures 3A and 3B on right side, when the optical center, O' not on the datum line, the farthest peak P' will at a different location, the radius of the MBS will be O'P'. The formulas do not calculate that correctly. As the optical center is moved to different positions within the frame contour, the farthest peak may change its position.
Often the patient's pupil center (the line of sight) is not on the datum line and commonly the optical center is best located 3 mm to 4 mm below the pupil. That requires moving the optical center accordingly, especially for high prescriptions, anisometropia, and aspheric lenses. The current formulas cannot calculate for a vertical movement of the optical center.
In formula, the decentration is defined as the distance from the optical center of the lens to the geometric center of the frame. Such a decentration has no prismatic effect. However, according to many references, the decentration should have prismatic effect. The decentration should be the more accurately defined as the distance from the optical center of the lens to the pupil center (the line of sight) [19-22]. The reference point for the decentration should be the pupil center (the line of sight) rather than the geometric center of the frame. This chart adopts the more accurately definition of the decentration.
In most cases, the optical center should coincide with the pupil center (the line of sight) to avoid unnecessary prismatic effect that can cause visual discomfort (asthenopia) or double vision (diplopia). However, in cases requiring a prismatic component to the visual correction, decentration can be used to create a prismatic effect. If that prism can be created by the decentration of a stock lens, it will simpler and less costly than ordering a specially surfaced one. This chart can easily determine the MBS with any decentration.
The weight, thickness and finishing time of the finished lenses of a pair of eyeglasses is directly related to the MBS. The MBS is determined by two factors: patient’s factor, PD and decentration, and frame’s factor, size and shape. Only the frame’s factor can be managed for a given prescription. We suggest that during selecting a suitable frame, all the potential candidate frames, especially for high power prescription, should be checked with this chart to make sure if the MBS for the chosen frame is within the three commercially available stock lenses.
Contemporary frames have so many different shapes and sizes that the listed frame dimensions, such as the A measurement, B measurement, DBL and ED, cannot precisely match their shapes and sizes, and are poor correlates to determine the MBS. This chart bypasses using frame measurements in determining the MBS. In addition to formulas, some drawing charts has been briefly introduced to calculate MBS, but there had not been a practical chart for dispensing eyeglasses in clinic. Therefore, we have designed this graphically instinctive and intuitive chart for determining the MBS for a selected frame. This chart can determine the MBS for a wide range of PDs from 40 mm to 75 mm.
The authors thank Wenyan Xu and Enting Song for their assistance with data collection.
This study was financially supported by National Key R&D Program of China (2020YFC2008200) and Wenzhou Science and Technology Bureau Basic Research Funding (Y20210996).
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
Citation: Chen J, Wang JY, Scott C, Wang GY, Li X, Wang GJ (2023) A Chart for Determining Minimum Blank Size of Spectacle Lens. J Clin Exp Ophthalmol. 14:960
Received: 01-Sep-2023, Manuscript No. JCEO-23-25972; Editor assigned: 04-Sep-2023, Pre QC No. JCEO-23-25972 (PQ); Reviewed: 18-Sep-2023, QC No. JCEO-23-25972; Revised: 25-Sep-2023, Manuscript No. JCEO-23-25972 (R); Published: 02-Oct-2023 , DOI: 10.35248/2155-9570.23.14.960
Copyright: © 2023 Chen J, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.