Journal of Biomedical Engineering and Medical Devices
Open Access
ISSN: 2475-7586
ISSN: 2475-7586
Research Article - (2018) Volume 3, Issue 2
Gait asymmetry is characterized as the dynamic differences between contralateral limbs, it has been shown to be caused by disease, age, clinical interventions and limb dominance. In this study, a mobile gait assessment system was developed for the evaluation of gait asymmetry in persons with simulated leg length discrepancy (sLLD). LLD is a disorder that affects 40-70% of the population requiring clinical intervention when the dissimilarity between limbs exceeds 3.7%. In out of clinic applications, an ambulatory gait symmetry system may be used to monitor postsurgical outcomes based on objective temporal and kinetic features. For this, a wireless gait symmetry system was designed and tested to measure ground reaction forces from insole worn pressure sensors. Thirteen metrics were extracted from a group of 9 subjects and a linear discriminant analysis performed for feature selection. Machine learning classifiers were used to differentiate between normal walking and sLLD. Applying majority voting to an Ensemble AdaBoost Tree classifier resulted in an overall accuracy of 89.9%, a false positive rate of 3.9%, and a sensitivity of 83.6%. Results indicate the wearable sensor is a viable option for out-of-clinic monitoring of asymmetry using machine learning.
Keywords: Gait asymmetry; Ground reaction forces; Leg length discrepancy; Wearable sensors; Machine learning; Majority voting
Leg length discrepancy (LLD) is a disorder which affects 40 to 70% of the population [1], requiring medical intervention when the unilateral discrepancy exceeds 2 cm or 3.7% [2,3]. Symptomatically LLD leads to gait asymmetry throughout gait: with changes in cadence, increased energy consumption, and abnormal ground reaction force distributions as the center of mass is abnormally displaced along the plant of the foot [4,5]. Conditions that arise as a cause of LLD include lower back pain, hip pain, and stress fractures [6,7]. LLD can be etiologically sectioned into prenatal events, such as dislocations, infections, and hemihypertrophy leading to developmental abnormalities. LLD may also be acquired in the case of surgeries, cancer and degenerative disorders [8]. Further classifications can be drawn between structural and functional causes, or differences in bony structure and gait asymmetries caused without osseous discrepancies. The most accurate method for diagnosing LLD is radiography followed by computer tomography; these two methods offer the highest resolution, allowing the detection of inequalities as low as 1 mm. Although sensitivity is high, radiation exposure, high costs, and the need of a technician for analysis deters implementation [8]. Consequently, LLD is most commonly examined using a tape measure, palpating of body landmarks or using lift blocks; these methods suffer from great controversy and are prone to loss of accuracy due to variation caused by subjective measurements [1].
The rapid growth of wireless, wearable sensors for gait analysis pose an important shift away from the common non-ambulatory methods used to analyze locomotion. In the last decades, gait analysis has been constrained to studies involving motion capture and the obligatory body markers and force mats. These constraints limit normal locomotion and remove important variation representative of each individual’s gait [9]. In addition to the behavioral constraints added by the non-mobile common gold standard measurement tools, high prices also deter medical professionals from making motion studies common practice [8]. Several commercial retailers offer gait analysis systems that promise to cover the void in mobility associated with lab-bound methods. Yet, no significant clinician or at-home implementation has been undertaken, due largely to high costs and undue complexity in results analysis and relative low cost efficiency, with the two major consumer ground reaction force (GRF) insole systems, F Scan (Tekscan, Boston, Ma) and Pedar (novel, Munich, Germany), costing thousands of US dollars. The Pedar is limited to 2 GB of local storage during wireless recording, while the F Scan is limited to tethered, wireless or data logging, and its wireless data logging is limited by battery consumption to two hours. In essence, these constraints limit these devices to either short recording sessions or the compromise between wireless streaming and short wireless data recordings [10]. This study was purposed to design and prototype a wearable, wireless, GRF gait symmetry analysis system that may smartly detect sLLD. A proposed solution to the classlabel problem, inherent to AdaBoost Ensemble learners, was explored with the implementation of majority voting after weighted voting for finding a minimal step count for detection.
Techniques for assessing LLD are commonly segmented into clinical and imaging modalities. The two most common clinical methods include lift blocks and the tape measure; these methods are useful screening tools that offer a quick, non-invasive diagnosis. However, these are less reliable than imaging modalities and suffer from empirical measurement errors. Imaging modalities include; radiography, computed radiography, ultrasound, computed tomography (CT) scanogram, and MRI scan [8]. Except for ultrasound and MRI, these imaging technologies expose the subject to radiation. These also incur an additional cost to the patient and the medical professional due to the high cost of acquisition, maintenance, and special equipment and staff needed for operation [8]. Additionally, a recent study found no correlation between CT scanogram and the clinical measurement methods (i.e., tape measure and lift blocks) for LLD detection, resulting in different diagnosis results [11]. Additionally, Badii et al. found low intraclass correlation coefficients when assessing interobserver reliability for the tape measure, as compared to radiography [12]. Medical professionals may not have access to high performing imaging modalities, unfortunately resorting to outdated clinical measurement tools due to the disadvantages mentioned above. The dissonance between the clinical and imaging modalities may be resolved by wearable sensors capable of objective measurements in a non-invasive and relatively cheaper manner.
To the authors’ knowledge, the most recent and comparable studies regarding wearable gait analysis focus on using inertial measurement units or pressure sensors to assess asymmetry in gait [13-15], extract gait features [16-19], or differentiate other disease states [20-24]. Past studies have explored real and sLLD using wearable inertial measurements (IMU) units [25,26], or using non-mobile motion capture systems [6]. There is no study yet using low-sensorcount, in-shoe, wireless pressure sensors. We proposed to employ a low-cost, low-sensor-count, in-shoe piezoresistive system for GRF, instead of IMU-based asymmetry based measurements, as previous studies revealed that LLD leads to significant changes to gait in ground reaction forces and their kinetic components [3,27-30], which can’t be measured by IMU sensors.
The experimental design in this study was in line with past studies using simulated leg length discrepancy (LLD) to analyze changes in gait. Assogba et al. demonstrated that both people with real and sLLD utilize similar compensatory techniques to limit energy expenditure [31]. Young et al. found that the lateral flexion taken from subjects with sLLD are similar to radiography measures for subjects with clear LLD [32]. Cumming et al. found anterior rotation of the ilium on the short leg in both simulated and real LLD [33]. Furthermore, Cooperstein’s review found that posterior innominate rotation in the anatomically long leg is apparent in both simulated and real LLD [34].
The spatiotemporal, kinetic, and kinematic metrics associated with the paired motion of lower limbs have also been successfully implemented with artificial intelligence (AI) paradigms to efficiently categorize disease states through non-invasive quantitative approaches [35]. The advantage of using AI is the ability to classify highly dimensional non-linearly separable data sets, as well as the ease by which new data can be used to improve the classifiers’ performance [36]. For the problem of pattern recognition, supervised learning aims to find a function representative of training sample pairs. Such learning algorithms may be divided into memory-based and nonmemory- based learning. Memory-based methods include k-nearest neighbors, kernel regressions, and support vector machines (SVMs). These rely on storing all data and inferring directly from neighboring samples to make a prediction on the classification of new data [37]. Non-memory-based methods include artificial neural networks, decision-tress, and naïve Bayes classifiers. These rely on capturing the function representative of the training sample pairs before new data is offered for classification [38]. Both memory and non-memory-based algorithms suffer from relying on a single hypothesis, derived from the training space. This proves problematic when several suggested hypotheses provide the same accuracy based on training data, or when algorithms get stuck on local minima due to computational constraints [39]. Ensemble methods solve this issue by providing new training data in an iterative manner based on votes from suggested hypotheses and thus, generating representative functions which may lay outside the training space and average similarly accurate hypotheses solving the computational and statistical problems. A recent comparison between memory, non-memory-based, and ensemble supervised learning methods found that boosted tress performed better than the rest [40] (Figure 1).
Device architecture
To wirelessly collect data and extract GRF metrics from gait, a wearable symmetry analysis system was designed, prototyped and tested. The device depicted on Figure 1a shows the size of the system and Figure 1b shows the mounting on the lateral part of the foot. The system employs a CC3200 low-power Wi-Fi module for wireless communication. This Texas Instruments Internet-of-Things prototyping platform has a 12-Bit ADC and 256 kB of RAM. Onboard data recording is built-in with a micro-SD flash card capable of memory expansion up to 512 GB. This ancillary data acquisition route takes precedence when wireless data streaming is either not guaranteed or needed. A power-path management IC was used for charge, voltage, and temperature measurements. Bipolar power was established to feed an MCP6004 Op-Amp, through a negative-output low-dropout linear regulator [41]. The insole shown in Figure 2 shows the force-sensing insole, comprised of three Tekscan A301 piezoresistive transducers capable of sensing between 0 to 445 newtons with 3% linearity error, 2.5% repeatability and 4.5% hysteresis at 80% full force application. As recommended by the manufacturers, calibration of the transducers was performed using a dual source inverting Op-Amp setup. Known loads were applied and the output values were recorded to identify the calibration relationship.
Experimental design and participant selection
The study was conducted in the Human Cyber-Physical System Laboratory with Institutional Review Board approval from Florida International University, Miami, FL. Nine participants, between 21 and 31 years of age, without previous musculoskeletal diagnoses or LLD were asked to walk along a 120 m walkway at comfortable walking speeds while wearing the wireless gait analysis system. Unaltered walking was considered symmetric and set as the ground truth against which sLLD would be compared. Similar to Khamis and Mahar [6,42], LLD was simulated using a shoe spacer (Evenup Shoe Balancer. Buford, GA) worn on the right foot, which applied 2.5 cm of length inequality to the user’s leg (Figure 1b).
Automatic gait cycle segmentation
For this study, we designed an automatic phase segmentation algorithm which extracts five features – heel contact, maximum heel contact, midstance, maximum toe contact, and toe off – from the pressure data to segment the gait cycle into four phases – heel strike, flat foot, heel off, and swing. This algorithm employs a user-defined threshold, which is used to allocate a value of 1 to data over the threshold and a value of 0 to data under the threshold. This binary signal is differentiated into positive spikes that indicate the heel contact and negative spikes that indicate the toe off, which result in the start and stop of the stance and swing phases. A midstance is approximated by measuring the halfway point between the heel contact and the toe off. From these two phases, the maximum heel contact is extracted by evaluating the maximum pressure value between the heel contact and the midstance. Likewise, the maximum toe contact is extracted by evaluating the maximum pressure value between the midstance and the toe off. From these two pressure peaks, the loading response, preswing, and flat foot phases are obtained (Figure 2).
Metric extracion
Thirteen metrics were evaluated to explore the gait asymmetry in kinetic and temporal features. The insole shown in Figure 2 shows the position of the pressure sensors, with the blue circle indicating the position of the sensor at the heel, the orange circle indicating the sensor at the medial lateral position, and the yellow circle indicating the sensor at the toe position. The pressure sensors were sampled at 125 Hz. Human locomotion examined using ground reaction force systems has slow dynamics: previous studies have used about 100 Hz sampling; based on these studies we determined 100 Hz for walking would be sufficient [43,44].
The metrics extracted from the wearable system designed in this study were: Difference in single stance time duration, ΔTDs(i) which shows the discrepancy between the right foot TDsL (i) and left foot TDsL (i). It is expected for this metric to be a clear indication of limping due to the added foot spacer on the right leg, leading to less weight acceptance on the left leg [4].
 (1)
(1)
where i is the i-th single support within a gait cycle, hc is the heel contact, and to is toe off.
Equations (2)-(4) show the difference in mean stance pressure, calculated between midstance and terminal stance when the weight of the body is completely shifted from the heel to the toe, showing the right to left comparison between total pressure at each pressure sensor during each stance time on heel ΔPh _ s, on medial-lateral ΔPM _ s, and
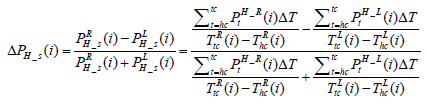 (2)
(2)
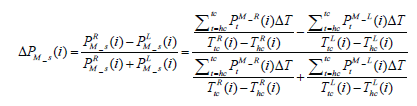 (3)
(3)
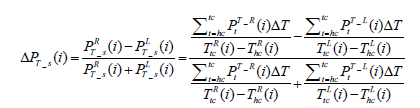 (3)
(3)
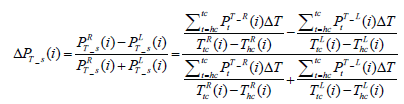 (4)
(4)
where PH is the pressure on heel, PM is the pressure on medial lateral, PT is pressure on toe and tc stands for toe contact.
Equation (5) and (6) show the difference in sagittal pressure distribution; on medial-lateral to heel ΔRPM-H and on medial-lateral to toe ΔRPM-T, which indicate the asymmetry from left to right pressure, while the weight of the body is shifting from the heel to the toe.
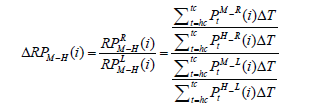 (5)
(5)
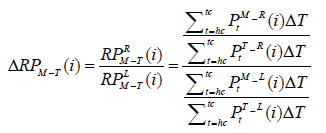 (6)
(6)
Equation (7) and (8) show the difference in peak heel contact pressure ΔPP-hc and difference in peak toe contact pressure ΔPP-tc, measured at terminal stance, indicating the pressure asymmetry during maximal pressure exertion.
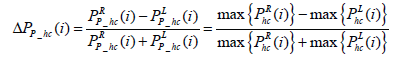 (7)
(7)
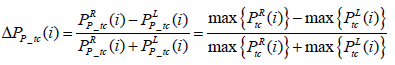 (8)
(8)
Equation (9) and (10) show the difference in the heel reposition time ΔTHR and in the toe reposition time ΔTTR indicating the asymmetry the time needed to achieve maximum loading response after initial heel contact, from right to left foot.
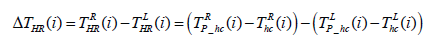 (9)
(9)
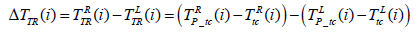 (10)
(10)
Equation (11) shows the difference in the time duration from heel to toe displacement ΔTDHT shows the asymmetry of duration between maximum pressure exertion, by heel and toe, between the right and left foot.
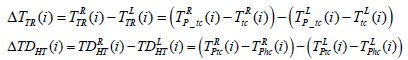 (11)
(11)
Ratio difference of loading ΔRLE and unloading effect ΔRULD in equations (12) and (13) show how much force is exerted during heel contact and how much force is exerted during toe-off as compared between right and left foot, in the case of loading depending highly on the preceding contralateral toe off behavior.
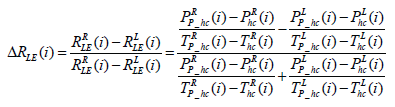 (12)
(12)
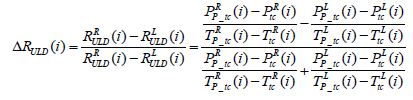 (13)
(13)
Dimensionality reduction
Since the thirteen-metrics extracted are not necessarily uncorrelated, feature selection was performed to determine features with larger interclass variation, i.e., larger differences between normal and LLD classes. The feature extraction was intended to avoid an overfitting problem in succeeding LLD classification as well as to improve computational efficiency.
In order to reduce correlated features that do not provide classification improvement, feature selection was performed through a linear discriminant analysis (LDA) [45]. As stated by Izenman, inclusion of a high-dimensional data containing correlated variables introduces collinearity leading to overfitting [46]. Performing Fisher’s LDA allows for the selection of discriminant variables based on separability between classes. LDA was used due to its ability to select the features which best separated the two classes of gait. Features were also ranked by maximization between class differences based on t-test results; this ranking was used to assess which metrics are more accurate for sLLD detection.
sLLD Detection using Machine Learning (ML) classifiers
Several of these machine learning-based classifiers, including decision tress, artificial neural networks, support vector machines (SVMs), genetic algorithms, etc. have been used to differentiate disease states [47], and even segment motion data by classifying gait phases [48]. In the events of data, which is closely related, as in the case of low sLLD, separation may prove difficult, leading to classification models with low predictive accuracy. However, evaluating the results from several classifying algorithms with low accuracy has proven to yield stronger classification results [49]. For this study, support vector machines, whose aim is to fit an optimal hyperplane between data sets [50], as well as boosting, a type of meta-algorithm used on decision tress and discriminant analysis learners to improve classification by adapting weights to sort gait cycle features, were explored to generate state prediction models. The classification results obtained from these models were then used to find an average step count from which majority voting could be used to further improve gait classification.
Support vector machines: The main theory behind SVMs has been extensively discussed and implemented into classification through gait of young and old subjects [36,47,51], patellofemoral pain syndrome [52], and gender [53]. This algorithm uses training data to create separating vectors based on neighboring data. In the case on non-linearly separable data, a kernel is implemented to map data to higher dimensional feature space, where data is linearly separated and a hyper-plane is returned to the original space for classification. This study explored linear, Gaussian and polynomial kernels to determine a better sLLD detection performance.
Ensemble boosting: Ensemble learning refers to the method based on the training of several low accuracy classification algorithms to build an incrementally better performing classifier [54]. The Adaptive Boost algorithm (AdaBoost), developed by Freund and Schapire [55], is a method which applies weights to miss-classified samples, then reduces the error in subsequent iterations. As mentioned by Dietterich, ensembles tend to lead to better classifier functions based on statistical averaging from votes provided by individual hypotheses, leading to a good approximation of the true classification hypothesis. Convergence at different local maxima may also prove problematic; ensembles solve this by composing a hypothetical function based on an average of the different local maxima. This hypotheses averaging also allow for the creation of new classifiers that may not be produced based only on the training data and the trends represented by it [54].
Supervised training and data processing: The leave-one-out standard for cross-validation (LOOCV) was followed to ensure training was completely separate from testing data. This strategy involves training the classifiers using all subjects except for the one whose data will be used for testing. This strategy ensures subject-independent classification, helps reduce with overfitting, and increases the usefulness of the results. However, LOOCV also leads to less accurate classifiers due to the high variability of gait within and between subjects.
Training data S={(x1,y1),…...(xn,yn)} from the all-but-one subject, with input xi and class labels yi ∈ {-1(Normal), 1(LLD)}, is offered to the learners. The learners were then tuned by branch size or iterative count and learning rate. This procedure leads to convergence of correctly labeled samples but also increases computation time. Majority voting was employed to average consecutive steps and their interaction, in order to find a minimum step count from which a proper estimation of sLLD could be made.
Majority voting for gait cycle polling
Consecutive gait cycles were selected from the automatic gait cycle segmentation algorithm and used in the voting rounds. Majority voting was then applied to the first round of classifiers in groups of single (non-voting), 3, and 5 gait cycles, to polynomial and Gaussian SVMs as well as Ensemble AdaBoost discriminant and tree learners [49]. The employment of this technique was twofold. First, to poll successive gait cycles for the possibility of sLLD, as consecutive gait cycles may be undergoing a cancellation effect, or adaptation due to the applied sLLD [56]. Second, to deal with class-label noise inherent to AdaBoost learners, whose weighted voting favors misclassified samples in its iterative process leading to overfitting.
Performance analysis
Accuracy, sensitivity, and false positive rate were used to evaluate the effectiveness of the sLLD classifiers after majority voting. TP is the number of correctly detected sLLD samples, TN is the number of correctly classified normal samples, FP are normal samples incorrectly detected as sLLD, and FN are sLLD samples incorrectly detected as normal. The Matthews correlation coefficient (MCC) was used to gauge the agreement between target and predictions thus measuring the quality of the binary classifications, varying between -1 for perfect disagreement to 1 for perfect agreement [57].
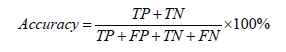 (14)
(14)
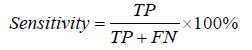 (15)
(15)
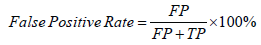 (16)
(16)
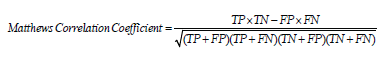 (17)
(17)
Piezo-resistive transducer calibration
Figure 3 shows the results of the calibration. The output voltage was found to follow a proportional relationship to the applied pressure. A 0.9916 coefficient of determination R2 for the linear relationship shows a good fit between the recorded response and the equation that represents the data recorded (Figure 3).
Feature analysis
Table 1 shows the feature selection after LDA and ranking based on statistical significance between classes. The testing accuracy shown is the average of all nine subjects for a polynomial SVM classifier. It can be noted that the best three performing metrics were loading rate (12), time to first peak (8), and stance time (1), with the first being a kinetic feature and the latter two being temporal. From best to worst performance, the feature selection ranking was as follows: loading rate, time to first peak, stance duration, push off rate, heel stance pressure, first peak pressure, medial lateral stance pressure, toe stance pressure, second peak pressure, pressure distribution form medial lateral to heel, time from second peak to toe off, time between maximum cycle peaks, and pressure distribution from medial lateral to toe.
| Metric | Equation | Single Vote Accuracy (± SD) |
T-test P-Value |
Ranking |
|---|---|---|---|---|
| Loading Rate, ΔRLE | (12) | 63.5 (9.5) | 2.87e-301 | 1 |
| Time to First Peak, ΔPp_tc | (8) | 64.6 (13) | 1.58e-242 | 2 |
| Stance Duration, ΔTDs | (1) | 66.9 (14.3) | 5.89e-233 | 3 |
| Push Off Rate, ΔRULD | (13) | 54.9 (9.1) | 2.36e-09 | 4 |
| Heel Stance Pressure, c | (2) | 46.5 (11.9) | 9.91e-09 | 5 |
| First Peak Pressure, ΔPp_hc | (7) | 57.1 (14.1) | 4.35e-08 | 6 |
| Medial Lateral Stance Pressure, ΔPM_s | (3) | 48.2 (16.4) | 1.94e-05 | 7 |
| Toe Stance Pressure, ΔPT_s | (4) | 49.9 (4.9) | 3.62e-05 | 8 |
| Second Peak Pressure, ΔTHR | (9) | 51.3 (2.4) | 4.11e-05 | 9 |
| Pressure Distribution Form Medial Lateral to Heel, ΔRPM-H | (5) | 56.9 (17.6) | 3.02e-04 | 10 |
| Time from Second Peak to Toe Off, ΔTTR | (10) | 52.3 (4.6) | 8.16e-04 | 11 |
| Time Between Maximum Cycle Peaks, ΔTDHT | (11) | 52.9 (13.7) | 1.25e-02 | 12 |
| Pressure Distribtuion From Medial Lateral to Toe, ΔRPM-T | (6) | 39.6 (12.3) | 4.18e-01 | 13 |
List of feature ranking showing 1loading rate, 2time to first peak, and 3stance time as being most sensitive to changes in leg length during gait
Table 1: Feature ranking based on SVM classification.
Classification results
From Table 2, it can be seen that the resulting data set was made up of 49 ± 7 samples for normal walking and 53 ± 6 samples for sLLD walking. Table 3 shows that using only stance duration for classification, the highest sensitivity and overall accuracy for all ML classifiers was achieved using Ensemble AdaBoost Decision Trees with a 5-vote majority rating. Training was performed with the highest three ranking metrics on the left column and using only loading rate on the right column. When using the first three ranked metrics, the overall accuracy was higher using 5-vote over no-vote polling with an average increase of 1.5%. Similarly, the false positive rate experienced an overall decrease of 67.3% after 5 votes over single voting. However, sensitivity decreased by 5.4% after 5 votes in comparison to non-voting. Interestingly, for all classifiers using the combinations of the first three ranked metrics, sensitivity suffered the largest decrease when attempting to decide based on 3 votes as opposed to 5. Within individual ML classifiers, polling 5 votes over no voting when using three metrics as opposed to 1 yielded the best accuracy increase and lesser sensitivity decrease for both Gaussian and polynomial SVM learners. Meanwhile, the largest false positive decreases were also achieved by the two SVM learners over 5-poll voting, however when using only 1 metric as opposed to 3. Both Ensemble AdaBoost learners showed the greatest accuracy jump after voting using only one feature, with the largest decrease in false positives and the smallest decrease in sensitivity. Additionally, the average MCC for all classifiers after LDA was 0.76, indicating a good overall binary prediction.
| Participant | Normal | sLLD |
|---|---|---|
| 1 | 41 | 61 |
| 2 | 56 | 57 |
| 3 | 39 | 44 |
| 4 | 42 | 45 |
| 5 | 57 | 57 |
| 6 | 49 | 49 |
| 7 | 53 | 53 |
| 8 | 42 | 48 |
| 9 | 58 | 60 |
Table 2: Data Set Sample Count Data sample count for each subject during each trial.
The overall best performing classifier was the Ensemble AdaBoost Tree, which after polling with 5 votes, achieved an overall accuracy increase of 3.4% to 89.9%, a 64.7% decrease in false positives to 3.9%, the smallest overall sensitivity decrease at 1.5% to 83.6%, and an MCC of 0.86.
This study focused on the technical feasibility and validity of using a wireless, GRF gait symmetry analysis system for simulated LLD detection. sLLD was employed according to the study providing that sLLD leads to gait changes without significant statistical differences with radiography diagnosed LLD [32]. Being able to control the amount of LLD ensures that the detection is effective for the targeted sLLD and not of other gait abnormalities. The results of this study demonstrate that even with a small population, merging machinelearning techniques dealt with the gait variability between subjects leads to a reliable detection of sLLD. The evaluation of different classifiers and the combination of majority voting allowed for the reduction of uncorrelated errors characteristic to gait between and within subjects.
Previous studies on sLLD have employed artificial neural networks for classification using non-mobile motion tracking systems reaching an overall testing accuracy of 83.3% when employing 30 coefficients, or features [58]. More recently, research on LLD continues to employ lab-bound imaging systems consisting of markers and force plates for the identification of LLD [56,59]. However, as the results of this study indicate, the implementation of ML classifiers to mobile-acquired metrics suggest a useful alternative owing to the flexibility of a wireless gait analysis system. The results also show an 89.9% overall accuracy while using a relatively small sample population and only requiring three metrics.
The type of ML classifier implemented for sLLD detection, showed the increase in sensitivity and accuracy and the decrease in false positives with majority voting depending on the number of metrics used. In the case of both discriminant and tree ensemble classifiers, a single feature was enough to provide the best classification models after voting, whereas both polynomial and Gaussian SVM demonstrated the largest increase in performance after voting for model accuracy and sensitivity when using three metrics. It has been shown that AdaBoost, the ensemble aggregation method used in this study, delivers poor probability estimates due to its inherent focus on outliers [40]. As proposed by Sabzevari, at high levels of class-label noise, the focus should be on instances on which the ensemble classifiers agree. Meanwhile, AdaBoost uses weighted majority voting on base hypotheses and favors misclassified instances in following iterations, leading to a majority vote that is heavily influenced by samples that are difficult to sort, which may lead to overfitting. In a recent study, voteboosting ensembles were introduced as an alternative means to deal with the class-label noise that affects AdaBoost ensembles. For voteboosting, the weights of hypothetical classifiers are determined based on the degree of agreement or disagreement among predictions [60]. In this study, the implementation of majority voting to the result of the weighted polling by AdaBoost, has shown to aid in the class-label noise issue characteristic to AdaBoost Ensembles. This was achieved by the elimination of uncorrelated errors of individual classifiers by averaging.
As performance of a classifier is highly dependent on the features chosen, linear discriminant analysis was used for dimensionality reduction based on correlation and maximization of class separation. As shown on Table 3, a three-dimensional training set was enough to differentiate between states of walking. This trend between classifier performance and low metric count has also been reported by other studies [36,52,61]. This may be caused by high correlation between metrics and or differing adaptive responses in gait by the addition of the foot spacer, also known as cancellation effect [56].
| Machine Learning Classifier | Metrics | All Features (No LDA) | 3 | 1 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Majority Vote | 1 | 3 | 5 | 1 | 3 | 5 | 1 | 3 | 5 | |
| Polynomial SVM | Sens (± SD) | 77.1 (14.3) | 50.4 (26.7) | 64.8 (22.0) | 80.9 (15.4) | 58.8 (29.3) | 70.6 (30.1) | 80.8 (17) | 62.1 (30.2) | 72 (29.9) |
| Fls Pos Rt (± SD) | 28.7 (23.7) | 7.3 (16.4) | 10.4 (21.9) | 13.5 (8.5) | 0.7 (2) | 1.2 (3.5) | 17.3 (13.6) | 2.8 (7.9) | 3.7 (10.5) | |
| Accuracy (± SD) | 74.2 (13.8) | 71.6 (17.9) | 77.2 (17.7) | 83.7 (9.1) | 79 (14.4) | 84.7 (14.5) | 81.7 (10.2) | 79.7 (14.5) | 84.2 (14.1) | |
| MCC (± SD) | 0.49 (0.28) | 0.49 (0.35) | 0.58 (0.35) | 0.74 (0.19) | 0.72 (0.17) | 0.82 (0.25) | 0.75 (1.7) | 0.74 (14) | 0.84 (0.25) | |
| AdaBoost Tree | Sens (± SD) | 75.8 (14.2) | 46.9 (27.9) | 62.8 (27.6) | 82.8 (13.3) | 64.3 (25.1) | 75 (24.3) | 86.2 (11.3) | 69.4 (22.1) | 83.6 (18.4)1 |
| Fls Pos Rt (± SD) | 26.5 (22.1) | 5.6 (11.6) | 7.5 (16.0) | 20.8 (16.3) | 2.8 (7.9) | 6.2 (14) | 18.2 (10.8) | 1.4 (3.9) | 3.9 (5.5) | |
| Accuracy (± SD) | 74.7 (9.3) | 70.6 (11.2) | 77.6 (13.2) | 81 (10.6) | 80.8 (11.9) | 84.4 (11.6) | 84 (8.9) | 84 (10.6) | 89.9 (9.1)2 | |
| MCC (± SD) | 0.52 (0.18) | 0.50 (0.19) | 0.61 (0.24) | 0.73 (0.18) | 0.69 (0.22) | 0.85 (0.21) | 0.75 (0.18) | 0.68 (20) | 0.86 (0.21) | |
1,2Results from the majority vote classifiers after dimensionality reduction by the LDA feature selector and the polling by sets of single votes, 3 votes and 5 votes
Table 3: Classifier results for joint sensitivity, false positive rate, and accuracy across polling.
It is interesting to note that the three metrics that vary most directly within gait sates were loading rate, time to first peak, and stance time, a kinetic-based feature which only requires the input from a single pressure sensor at the heel. While time to first peak and stance time are both temporal features, the latter may be extracted by one pressure sensor at the heel and one at the toe, and the former may be extracted by the same pressure sensor needed for loading rate. Begg et al. demonstrated that maximum and minimum forces plus normalized double support time were enough to differentiate between young and old subjects [61], indicating the need for the medial lateral pressure sensor in the case when maximum force is not observed at the toe. Meanwhile, in increasing ranking, the lowest three performing metrics were found to be, pressure distribution from medial lateral to toe (6), time between maximum cycle peaks (11), and time from second peak to toe off (10). Metric 6 is largely based on the sagittal asymmetry during weight bearing, whose effects may be masked by compensatory strategies employed by the subjects in an effort to retain balance. Metric 11 shows the difference in the time duration from heel to toe displacement. Since metric 1, which ranked third overall, is also a measure of the asymmetry between time taken for each step, compensatory strategies such as dynamic shortening of the affected leg may be occurring during weight transfer but not at initial load bearing or at push-off in an effort to minimize the displacement of the center of mass [3]. Metric 10 was ranked eleventh by the t-test and may help clarify at which stage of loading, load bearing or push-off, compensatory strategies were being employed. Since loading rate (12) was ranked first, this means it showed the greatest difference between normal and sLLD walking. It can be concluded that push-off did not experience such major changes due to the added foot spacer. This finding may be supported by strategies used to decrease energy expenditure [31]. Other studies have found that by default, step length may be more asymmetric than step times and should also be evaluated in future studies to improve classifier performance [56]. Future works will aim at performing a clinical feasibility study, comparing the developed system with gold standards, as well as implementing data from subjects with non-simulated LLD and other gait impairing disorders.
In this article, a mobile, smart gait assessment system was designed and tested for the detection of asymmetry in sLLD using machinelearning classification. Leave-one-subject-out cross-validation demonstrated a detection accuracy of 89.9% (± 9.1%) from nine subjects using pressure sensors on the insole for temporal and kinetic metric extraction. Results indicate that the wireless gait analysis system is a viable option for the detection of low-level asymmetry in an ambulatory setting. Future works aim to implement automatic detection to pathological subjects.
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
J. Sebastian Márquez, Roozbeh Atri, Masudur R. Siddiquee, and Ou Bai conceived and designed the experiments. J. Sebastian Márquez, and Masudur R. Siddiquee performed the data acquisition. J. Sebastian Márquez, Connie Leung, and Ou Bai wrote the algorithms for metric extraction and machine learning implementation. J. Sebastian Márquez Roozbeh Atri and Masudur R. Siddiquee analyzed the results. J. Sebastian Marquez wrote the article and Connie Leung revised the manuscript. All authors read and approved this manuscript.
All datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.
This study was partly supported by the National Science Foundation (CNS- 1552163). The authors would like to thank the volunteers who participated in the study.