Fisheries and Aquaculture Journal
Open Access
ISSN: 2150-3508
ISSN: 2150-3508
Commentary - (2017) Volume 8, Issue 3
We investigate a semi-contained, two-tank model for a Litopenaeus vannamei (White Pacific Shrimp) aquaculture farm. Our model simulates the possibility of a self-sustaining aquaculture system, with an interdependent triad of shrimp, algae, and bacteria. The two tanks are symmetric: the first containing developing shrimp through the hatchery and nursery phase and the second containing full grown shrimp through the grow-out phase. This system is modelled by six, first order differential equations. Using analytic and numeric techniques, we examine the dynamics and equilibria of this system as well as each of its individual components. This paper examines the effects of varying harvesting frequencies and magnitudes, and searches for an optimal harvesting strategy. Our analysis concluded that in the confines of our model, a technique of harvesting 81.5% of harvestable shrimp every 2 days provides a hypothetical optimal strategy. However, upon consideration of practical constraints, a harvesting strategy of 98% of harvestable shrimp every 10 days represents a real-world optimal harvesting strategy.
Keywords: Shrimp; Aquacultures; Seafood; Consumption; Production
Annual U.S. consumption of shrimp is upwards of 600,000 metric tons per year, with the average American consuming four pounds of shrimp annually, more than any other individual seafood product [1]. Aquaculture is the most common method of shrimp farming. This farming technique entails raising shrimp in enclosed areas of ponds, rivers, lakes and oceans. All forms of aquaculture, particularly for shrimp and salmon, negatively affect biodiversity by degrading habitats, disrupting trophic systems, transmitting diseases, and reducing genetic variability. Aquaculture farming typically requires the clearing of land to build proper raising grounds. The destruction of these environments has led to the subsequent extinction and endangerment of its inhabitants.
Shrimp aquaculture has a significant effect on surrounding waters. Shrimp grown in aquaculture require the continuous renewal of fresh water to adjust salinity and nitrogen levels. In Asian countries, freshwater is used at a rate of about 5.3 million gallons a year per acre of shrimp farm to control water quality, suggesting that such practices are unsustainable [2] in both enclosed and unenclosed shrimp aquaculture; the flushing of this water also causes significant environmental damage. Each acre of shrimp farms produces 3 tons of solid waste per year. This waste, in addition to the uneaten shrimp feed and cocktail of pesticides, additives, and antibiotics typically used to maintain the overcrowded shrimp populations, pollutes potable groundwater, coastal estuaries, and other nearby sources of water.
In response to the negative environmental impacts on shrimp aquaculture, Biofloc technology (BFT) emerged in the early 2000’s as sustainable and environmentally neutral system of shrimp production [3] while traditional aquaculture utilizes consistent and continuous water exchange to control water quality, Biofloc systems allow for the accumulation of microbial communities within its own indoor tanks. The microbial communities (referred to as Biofloc) employed in BFT can improve water quality, control pathogenic bacteria, recycle shrimp waste, and act as a continuously available food source for shrimp given sufficient mixing and aeration to keep active flocs in suspension [4]. Maintenance of water quality depends mainly on an active microalgae, free and attached bacteria, aggregates of living and dead particulate organic matter and microbial grazers maintained in suspension. Organic waste produced by growing shrimp are controlled by a combination of phytoplankton uptake, nitrification, and by heterotrophic bacteria immobilization inside the culture unit. Thus, the use of Biofloc technology allows farmers to significantly reduce both their usage of freshwater, and the environmental detriments accompanied with flushing said freshwater. Growing Biofloc also serves as source of nutrients for growing shrimp, significantly or completely reducing the usage of fishmeal. As a result, Biofloc systems provide two critical resources: a continuous, cheap food source and waste treatment.
Within the last two years, Biofloc systems have become increasingly popular amongst U.S. shrimp farms. However, commercial farms have yet to implement self-sustaining versions of Biofloc systems. Currently, most farms import shrimp larvae from hatcheries and oversee the nursery and grow-out phases before harvesting. However, recent developments in shrimp farming technology have enabled farmers to efficiently oversee shrimp from the hatchery phase to harvesting. Specifically, recent literature has found that Pacific White Shrimp ( Litopenaeus vannamei ), the most consumed species of shrimp in the United States, can be bred in the off-season and in subtropical conditions. This development would enable farmers to breed their own shrimp as opposed to importing them from coastal hatcheries [5]. Due to the low salinity sensitivity of Pacific White Shrimp, this discovery suggests the possibility of developing self-sustaining Pacific White Shrimp farms in unconventional regions far from coastal regions and natural breeding grounds.
More over Emerenciano et al. [6] has found that some shrimp can live entirely off of Biofloc, as opposed to a combination of fishmeal and Biofloc. To isolate and simplify the effects of Biofloc on the growth of Pacific White Shrimp, our model uses the mutualistic relationship between the similar types of microalga and marine bacteria found in Biofloc as the main interaction that occurs with the shrimp. Building on current literature on Biofloc-based Shrimp farms, the microbial communities used in these systems, and shrimp hatchery methods, this paper proposes a model for a self-sustaining shrimp farm in which shrimp are birthed, raised, harvested, and fed entirely on Biofloc.
In our model, two separate, semi-contained tanks are used, linked by bilateral transfer of shrimp due to reproduction and maturation. This structure was chosen as the farming of Pacific White Shrimp involves three main phases: Hatchery, Nursery, and Grow Out. The Hatchery phase grows the shrimp from egg to early Post Larvae. Most farmers have found that including a separate Nursery tank that grows the shrimp from early Post Larvae through Juvenile to be effective in decreasing mortality and increasing size, although it is not necessary to produce profitable yields (Figure 1).
Figure 1: Semi-contained, two-tank model for a Litopenaeus vannamei aquaculture farm. B1=Bacteria Population in Maturing Tank (1012 cells); S1=Maturing Shrimp Population; A1=Algae Population in Maturing Tank (kg); B2=Bacteria Population in Harvestable Tank (1012 cells); S2=Harvestable Shrimp Population; A2=Algae Population in Harvestable Tank (kg).
As a result, we will not include this tank in our model. Lastly, the Grow Out phase grows the shrimp from Juvenile through adult, producing marketable shrimp. Such a structure is necessary due to the differing conditions required for shrimp at different phases.
Bacteria Growth in Maturing Tank=Logarithmic growth factor * Bacteria population in maturing tank * [1 - Bacteria population in maturing tank / (Bacteria carrying capacity factor * * Maturing shrimp population + Epsilon)]
Algae Growth in Maturing Tank=Logarithmic growth factor * Algae population in maturing tank * [1 - Algae population in maturing tank / (Algae carrying capacity factor * Bacteria population in maturing tank + Epsilon)] - (Maturing shrimp consumption * Maturing shrimp population)
Maturing shrimp growth=(Shrimp reproduction * Harvestable shrimp population) - {Death rate * Maturing shrimp population * [(Half consumption * Maturing shrimp population) / (Algae population in maturing tank+epsilon) + 1} - (Transfer factor * Maturing shrimp population)
Harvestable shrimp growth=(Transfer factor * Maturing shrimp population) - {Death rate * Harvestable shrimp population * [(Half consumption * Harvestable shrimp population) / (Algae population in Harvestable tank +epsilon) + 1} - (Harvesting factor * Harvestable shrimp population)
Bacteria growth in harvestable tank=Logarithmic growth factor * Bacteria population in harvestable tank* [1 - Bacteria population in harvestable tank / (Bacteria carrying capacity factor * Harvestable shrimp population * Epsilon)]
Algae Growth in Harvestable Tank=Logarithmic growth factor * Algae population in harvestable tank * [1 - Algae population in harvestable tank / (Algae carrying capacity factor * Bacteria population in harvestable tank+ Epsilon)] - (Harvestable shrimp consumption * Harvestable shrimp population).
Constants and terms explained
D1=0.0007 * VS11 − 0.0099=0.0000035 * S1 − 0.0099
We fit a linear trendline to the below data, provided by Lorenzo et al. [6], which gave us Hatchery death, D1, as a function of Larval concentration, (S1/V1). Using our maturing shrimp tank volume, V=20,000 liters, we obtained the above equation. The linear fit, with an R2 value 1 of 0.997, is shown below (Table 1 and Figure 1).
| Larval Density (Larvae/liter) | Larval Death in Hatchery Phase |
|---|---|
| 200 | 12.96% |
| 300 | 19.43% |
| 350 | 23.45% |
Table 1: Hatchery death as a function of Larval Density in BFT system [7].
D2=0.0048 * VS22 − 0.3983=0.000048 * S2 − 0.3983
We fit a linear trendline to the below data, provided by Treece [7], which gave us Grow out death, D2, as a function of shrimp concentration, (S2/V2). Using our harvestable shrimp tank volume, V2=20,000 liters, we obtained the above equation. The linear fit, with an R2 value of 0.862, is shown below (Table 2 and Figure 3).
| Shrimp Concentration (Shrimp/Litre) | Shrimp Death in Grow Out (Harvestable) Phase |
|---|---|
| 25 | 50.60% |
| 30 | 56.20% |
| 39.3 | 58.20% |
| 39.3 | 58.60% |
Table 2: Grow out death as a function of shrimp Density in BFT system [8].
D2=0.0048 * VS22 − 0.3983=0.000048 * S2 − 0.3983
We fit a linear trendline to the below data, provided by Treece [7], which gave us Grow out death, D2, as a function of shrimp concentration, (S2/V2). Using our harvestable shrimp tank volume, V2=20,000 liters, we obtained the above equation. The linear fit, with an R2 value of 0.862, is shown below.
The constants used in our model can be explained in Table 3.
| Constant | Significance |
|---|---|
| k1 | Logarithmic Growth Rate of Bacteria in both Tanks |
| k2 | Logarithmic Growth Rate of Algae in both Tanks |
| k23 | Rate of Algae Consumption in Maturing Tank |
| k34 | Percent of offspring Maturing and Transferred to Harvestable Tank |
| k43 | Average number of offspring produced by harvestable shrimp per day |
| k64 | Rate of Algae Consumption in Harvestable Tank |
| kc1 | Effect of Algae Presence on the Death Rate of Shrimp (represented but unlabeled in box model) |
| kc2 | Half of Amount of Adequate Algae for Harvestable Shrimp (Half of kc1 ) (represented but unlabeled in box model) |
| kh | Percentage of Shrimp Harvested from Harvestable Tank |
| c1 | Factor Relating the Population of Maturing Shrimp to the Carrying Capacity of Bacteria in the Maturing Tank (represented but unlabeled in box model) |
| c2 | Factor Relating the Population of Bacteria to the Carrying Capacity of Algae in the Maturing Tank (represented but unlabeled in box model) |
| c5 | Factor Relating the Population of Harvestable Shrimp to the Carrying Capacity of Bacteria in the Harvestable Tank (represented but unlabeled in box model) |
| c6 | Factor Relating the Population of Bacteria to the Carrying Capacity of Algae in the Harvestable Tank (represented but unlabeled in box model) |
| Ɛ | An Arbitrarily Small Constant to Prevent the Dominator From Being Zero |
Table 3: Constants used in model shown in Figure 1.
k1=15.42
k1 represents the logarithmic growth rate of bacteria in both tanks. We found this number by averaging out the Specific Growth Rates found in White et al. [9] for strains of marine bacteria exposed to varying types of aquatic habitats. This makes sense due to the fact that this study examined bacteria growth in ideal conditions. This means that the term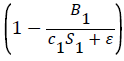 in the equation for B′1 can be assumed to equal 1, as the carrying capacity was not a factor in this study. In the case where
in the equation for B′1 can be assumed to equal 1, as the carrying capacity was not a factor in this study. In the case where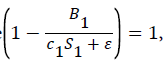 k1represents the logarithmic growth rate of bacteria, which was found to be 15.42.
k1represents the logarithmic growth rate of bacteria, which was found to be 15.42.
k2=0.4
k2 represents the logarithmic growth rate of algae in both tanks. From a study done by Assavaaree et al. the average doubling time for Skeletonema costatum when tested in varying degrees of saltwater was 1.73 days. This corresponds to a logarithmic growth rate of 0.4. This makes sense due to the fact that this study examined algae growth in ideal conditions, in an environment supplemented by vitamin B12, a key compound that our nitrogen fixing bacteria are producing in our ecosystem. This means that the term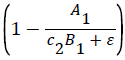 in the equation for A′1 can be assumed to equal 1, as the carrying capacity was not a factor in this study. In the case where
in the equation for A′1 can be assumed to equal 1, as the carrying capacity was not a factor in this study. In the case where 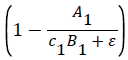 = 1, k2 represents the logarithmic growth rate of algae, which was found to be 0.4.
= 1, k2 represents the logarithmic growth rate of algae, which was found to be 0.4.
k23=0.000004
k23 represents the rate of algae consumption by shrimp offspring. Research on the diet of shrimp revealed that typical algae consumption by adult shrimps is approximately 0.02 g per shrimp per day [10]. In our model, the unit of algae is kilograms, meaning that this translates to 0.00002 kg per day. However, minimal data is present regarding algae consumption rates for shrimp offspring. Thus, we had to make an assumption. Maturing shrimp have approximately one fifth the body mass of fully matured shrimp, so we made an assumption based on this. As a result, we used 0.00002/5 kg per day, or 0.000004 kg of algae per day.
k34=0.008333
k34 represents the fraction of offspring growing up and being transferred to the full-grown tank at any given time. As we use a box model and not an agent based model, it is impossible to know the age/ growth of any individual shrimp at any given time. This required us to make a generalization. It takes 120 days for a shrimp to develop sufficiently to be transferred to the full-grown tank [11]. Thus, on average, 1 out of every 120 will be maturing at any given time. Thus, k34 equals 1/120, or 0.008333.
k43=11.0164
k43 represents the average amount of offspring produced per shrimp per day. A variety of information was used to estimate this number. Firstly, shrimp live for around two years, or 730 days, on average [12]. Additionally, shrimp do not transfer into the full-grown tank until day 120. Thus, shrimp spend about 610 days of their life with the ability to reproduce. Furthermore, shrimp reproduce around three times over their lifespan, and produce approximately 2,240 offspring each time [5]. Thus, the likelihood that any given shrimp is reproducing on any given day is 3/610, or 0.004918. This gets multiplied by the average number of offspring produced, 2,240, to give us 11.0164 offspring produced on average per shrimp per day.
k64=0.00002
k64 represents the rate of algae consumption by harvestable shrimp. As explained above, research on the diet of shrimp revealed that typical algae consumption by adult shrimps is approximately 0.02 g per shrimp per day [10]. In our model, the unit of algae is kilograms, meaning that this translates to 0.00002 kg per day.
kc1=0.000002
kc1 represents a value related to the effect of algae presence on the death rate of shrimp. The term 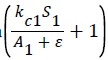 is multiplied by the deathrate in the ‘S’ equation. This term equals approximately 1 when there are plentiful algae per shrimp (as the denominator will be much greater than the numerator, making the term equal approximately 0+1. The kc1 term determines
is multiplied by the deathrate in the ‘S’ equation. This term equals approximately 1 when there are plentiful algae per shrimp (as the denominator will be much greater than the numerator, making the term equal approximately 0+1. The kc1 term determines 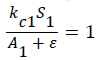 at what point resulting in the entire term equalling two. Thus, kc1 determines at what point the death rate doubles due to insufficient algae. Thus, we want
at what point resulting in the entire term equalling two. Thus, kc1 determines at what point the death rate doubles due to insufficient algae. Thus, we want  when the algae per shrimp is half of typical shrimp algae consumption. As discussed above, typical algae consumption by immature shrimp is 0.000004 kg per day. Thus, is makes sense that kc1 equals approximately half of that, or 0.000002.
when the algae per shrimp is half of typical shrimp algae consumption. As discussed above, typical algae consumption by immature shrimp is 0.000004 kg per day. Thus, is makes sense that kc1 equals approximately half of that, or 0.000002.
kc2=0.00001
Identical reasoning as with kc1, except that kc2 represents half of the adequate algae for full-grown shrimp, which is approximately half of 0.00002 kg per day, or 0.00001.
c1=0.004
c1 represents a factor relating the population of maturing shrimp to the carrying capacity of bacteria. To obtain an approximate value of this constant, maximum bacteria concentration per liter was examined. Bacteria in both tanks have a maximum concentration of approximately 1012 cells per liter, or 1 unit of bacteria per liter (units for bacteria population are 1012 cells/liter). We assumed this would only be sustainable if the shrimp population was also maximized, which in the case of maturing shrimp is 250 shrimp per liter. Thus, 250 times c1 should equal approximately 1, meaning that c1=0.004.
c2=0.05
c2 represents a factor relating the population of bacteria to the carrying capacity of microalgae in the maturing tank. To obtain an approximate value of this constant, maximum algae concentration per liter was examined. As algae grow along the floor of the tank, a maximum algae concentration of 5% of each liter, or 0.05 kg per liter, was approximated. We assumed this would only be sustainable if the bacteria population was also maximized, which is 1 unit of bacteria per liter, as discussed above. Thus, 1 times c2 should equal approximately 0.05, meaning that c2=0.05.
c5=0.04
c5 represents a factor relating the population of harvestable shrimp to the carrying capacity of bacteria. To obtain an approximate value of these constant, identical calculations were performed as with c1, except that harvestable shrimp concentration has a maximum value of 25 shrimp per liter. Thus, 25 times c5 should equal approximately 1, meaning that c5=0.04.
c6=0.05
Identical reasoning as c2 but applied to the harvestable tank.
Ɛ=0.0001
Ɛ represents a small constant that prevents the denominator of each fraction in our equations from going to 0.
In assessing varying harvesting techniques, we considered two variables:
i.) Frequency of harvest
ii.) Percent of harvestable shrimp harvested each in batch
We examined each of these variables and their effects on the aggregate quantity of shrimp harvested over 500 days, with a secondary consideration to the effects on the equilibrium of harvestable shrimp. We first chose to optimize the frequency of harvesting as this was not a continuous optimization as we assumed finite options of whole number days (such as harvesting every 3 days, or every 5 days, but not every 3.5 days). Then, following this optimization, we sought to optimize the size of each harvest.
Note: For the purposes of this analysis, the “level of equilibrium” is defined as the population size that is achieved immediately prior to harvesting as time goes to infinity. Additionally, “optimal harvesting technique” refers to the harvesting strategy that maximizes the output of harvested shrimp over our time period of 500 days.
i) In order to examine the effects of varying frequency of harvests, a default harvesting percentage of 90% was chosen, as well as default initial parameters of 8 * 1012 bacteria cells and 2 kg of algae per tank, in addition to 1,000 maturing shrimp and 100 harvestable shrimp. An examination of the effects of varying these parameters may provide additional insight into this aquaculture system, however they are beyond the scope of this paper.
Under these conditions, we examined harvesting frequencies of once every 1, 2, 3, 6, 10, 15, 20, 30, 50, and 100 days. The effects of these frequencies of harvesting on the quantity of shrimp harvested and the harvestable shrimp equilibrium are shown in the figure below.
As can be seen in Figure 4, increased frequency results in a greater magnitude of shrimp harvested up until a certain point, at which decreasing returns are achieved. On the other hand, increased frequency of harvest results in a lower equilibrium level of harvestable shrimp population in all cases.
To understand the first of these phenomena, three effects of increased harvesting frequency must be considered. Firstly, increased frequency results in greater total harvests achieved over the 500 day period. This primarily explains the fact that increasing the frequency of harvests results in increased quantity of shrimp harvested, as there are simply more batches of harvested shrimp. Secondly, increased frequency has effects related to the rate of shrimp population growth. This is due to the negative nature of the second derivative of the shrimp population (more simply put, the population growth slows as the population approaches a certain carrying capacity). Thus, a harvesting strategy that is insufficiently frequent will be inefficient due to the decreasing nature of shrimp population growth. Thirdly, increased frequency results in lower equilibrium levels of the harvestable shrimp population. Thus, although there are more total batches of harvested shrimp, each of these batches are smaller, as the shrimp population is smaller, and harvesting 90% of the harvestable population yields a smaller-sized batch.
Keeping these three factors in mind, a close examination of Figure 4 reveals that harvested shrimp quantity is maximized at a frequency of 2 days. However, there are some practical factors that may prevent this hypothetical ideal frequency from being most efficient in practice. These considerations are discussed later in our analysis.
ii) Having established bi-daily as the optimal frequency of harvesting, we turned our attention to an examination of the ideal fraction of the shrimp population to harvest in each batch. In order to study this, we used the optimal frequency of bi-daily harvests, as well as the same default initial parameters of 8*1012 bacteria cells and 2 kg of algae per tank, in addition to 1,000 maturing shrimp and 100 harvestable shrimp. Under these conditions, we examined harvesting proportions of 10, 20, 30, 40, 50, 60, 70, 80, 81.5, 83, 90, and 95 percent of the harvestable shrimp population at the time of harvest. The effects of these harvesting rates on the quantity of shrimp harvested and the harvestable shrimp equilibrium are shown in Figure 5 and Table 4 below.
| Percent Harvested Every Two Days | Aggregate Shrimp Harvested (Millions) |
|---|---|
| 10% | 2.1752 |
| 20% | 3.5118 |
| 30% | 4.507 |
| 40% | 5.0532 |
| 50% | 5.4273 |
| 60% | 5.6295 |
| 70% | 5.7182 |
| 80% | 5.7537 |
| 81.50% | 5.7547 |
| 83% | 5.7537 |
| 90% | 5.7298 |
| 95% | 5.7096 |
Table 4: Effect of varying harvesting percentage/rate on aggregate shrimp harvested (10 days).
As Table 4 shows, while the diminishing returns that are seen at harvesting percentages greater than 81.5% are not enormous, they are substantial (~50,000 less shrimp harvested) and they point to an interesting phenomenon. Similarly to what we saw in harvesting frequency, increasing the percentage of shrimp that are harvested results in gains up to a certain point, however, past this point, diminishing returns are seen and increased harvesting rates results in decreased yields.
Similarly to what was discussed in part i, increasing the fraction of harvestable shrimp harvested per batch have twofold effects. Firstly, and obviously, this results in larger batches when holding shrimp population at the time of harvest constant. However, a second result of increased shrimp harvesting rate is that the equilibrium population of adult shrimp is lower. This means that although each batch is taking a greater proportion of the shrimp population, the actual quantity harvested may be less if the population is smaller. This explains the trends seen in our data.
Combining the analysis of parts i and ii, under the given initial conditions, the optimal harvesting strategy is to harvest 81.5% of the harvestable shrimp population every 2 days.
Practical considerations
In order to analyse the practicality of our harvesting technique, it is imperative to first examine actual harvesting techniques used by shrimp farmers. As previously established, optimal harvesting frequency of our model is approximately once every two days. However, this harvesting technique would carry many practical implications. Identifying the shrimp that have reached harvestable size in the maturation tank would be a time consuming task if done every other day. Financially, the cost of harvesting bi-daily would also be incredibly high, as designated workers would need to be onsite to harvest, process, package, and transport the shrimp. Transportation would also need to be arranged to export the shrimp from the farm every two days. Looking at research on the financial optimization of biofloc technology shrimp farms with multiple tanks, we found that the smallest harvesting frequency was once every 10 days [13]. In particular, the variable costs of labour (both hired labour and management) significantly impact profitability when frequency is increased beyond this point, as they make up to 28% of the total operational costs [14]. With these practical considerations in mind, we examined varying harvesting proportions at a frequency of once every 10 days.
As depicted in Table 5, the effects of increased harvesting proportion of total shrimp yield is similar to the effects observed at a bi-daily frequency. Increasing the harvesting fraction results in increased total shrimp harvested up to a certain point, after which diminishing returns are observed. In this case, however, the optimal harvesting rate is approximately 98% [15]. The fact that this rate is greater than the 81.5% that was optimal under bi-daily harvesting is due to the fact that the reduced frequency minimizes the negative effects of increased harvesting rate on the shrimp equilibrium population. Thus, a greater harvesting fraction is sustainable and beneficial as the population has increased time to regrow between batches.
| Percent Harvested Every Ten Days | Aggregate Shrimp Harvested (Millions) |
|---|---|
| 50% | 1.965 |
| 70% | 2.525 |
| 90% | 2.925 |
| 95% | 3.004 |
| 97% | 3.023 |
| 98% | 3.062 |
| 99% | 3.061 |
Table 5: Effects of harvesting percentage/rate on aggregate shrimp harvested (10 days).
Thus, with practical limitations on frequency in mind, the optimal technique is to harvest approximately 98% of harvestable shrimp every 10 days [16-18]. Under these conditions, the harvestable shrimp population settles at an equilibrium value of approximately 100,000, and a total yield of 3.062 million shrimp are harvested over the 500 day period we examined. One final consideration is the reasonability of our model’s shrimp production. Medium to large scale commercial Pacific White shrimp farms that oversee solely the nursery and grow-out phase of the shrimp typically harvest 100,000 to 500,000 pounds of shrimp per year. This is equivalent to approximately 5 to 25 million harvested shrimp per year [19-24] In comparison, looking at Table 5, our model produced 2.19 million per year, which would be equivalent to the output of a small to medium scale farm, which is in accordance with the volume (20,000 liters) of our both the maturing and harvesting tanks. The tank size, combined with the factors that make our system self-sustaining, explain the slightly reduced output, and given these factors, the output appears reasonable.
In our analysis, we examined the effects of varying harvesting techniques in respect to frequency of harvesting and proportion of shrimp harvested on the aggregate yield of shrimp harvested [25-28]. The results of this analysis included a hypothetical optimal harvesting regimen, as well as a practical optimum. The hypothetical optimum was to harvest 81.5% of harvestable shrimp every two days. The practical optimum was to harvest 98% of harvestable shrimp every ten days [29-33]. This practical optimum shows many similarities to traditional shrimp farms, as one common technique involves farming 100% of harvestable shrimp every 10 days given a multi-tank farm [13]. The key difference is that our model strives to be self-sustaining, meaning that some harvestable shrimp must be left in the tank in order to reproduce.
Our conclusion of harvesting 98% of harvestable shrimp every 10 days shows promise for our model as an alternative to traditional shrimp farming. The benefits of our model are as follows. Firstly, there are significantly reduced operational costs due to the elimination of the need to outsource larvae and use fish meal. Secondly, there are significantly reduced environmental effects due to the lack of disposed biologic waste, uneaten fish meal, and the elimination of the need to clear coastland for farming. In addition to posing promise in regards to improvements over traditional farming methods, our model displays practicality and viability. Under harvesting techniques listed above, all involved populations oscillate around reasonable values, and the yields of shrimp harvests are substantial. Thus, our model represents a viable and valuable method of farming shrimp.
Further study regarding this aquaculture system could include an examination on optimal initial conditions, tank size, and varying strains of bacteria and algae. Additionally, further study into the practical viability of such a model, including tank dimensions, ability to transfer mature shrimp, and ability to effectively execute the given harvesting strategies may shed light on the value of this model. However, within the scope of this project, we conclude that this model is a promising alternative to traditional shrimp farming methods, and practical harvesting techniques in this system would be to harvest 98% of harvestable shrimp every 10 days.