Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2012) Volume 5, Issue 1
One of the important tools in analyzing and modeling biological data is the Hidden Markov Model (HMM), which is used for gene prediction, protein secondary structure and other essential tasks. An HMM is a stochastic process in which a hidden Markov chain called; the chain of states, emits a sequence of observations. Using this sequence, various questions about the underlying emission generation scheme can be addressed. Applying an HMM to any particular situation is an attempt to infer which state in the chain emits an observation. This is usually called posterior decoding. In general, the emissions are assumed to be conditionally independent from each other. In this work we consider some dependencies among the states and emissions. The aim of our research is to study a certain relationship among emissions, with a focus on the Markov property. We assume that the probability of observing an emission depends not only on the current state but also on the previous state and one of the previous emissions. We also use additional environmental information, and classify amino acids into three groups, using the Relative Solvent Accessibility (RSA). We also investigate how this modification might change the current algorithms for ordinary HMMs, and introduce modified Viterbi and Forward-Backward algorithms for the new model. We apply our proposed model to an actual dataset concerning prediction of the protein secondary structure and demonstrate improved accuracy compared to the ordinary HMM. In particular, the overall accuracy of our modified HMM, which uses the RSA information, is 63.95%. This is 5.9% higher than the prediction accuracy realized by using an ordinary HMM on the same dataset, and 4% higher than the corresponding prediction accuracy of a modified HMM that simply accounts for the dependencies among the emissions.
Keywords: Hidden Markov Models; Protein Secondary Structure Prediction; Relative Solvant Accessibility; Modified Viterbi Algorithm; Forward Algorithm
ASA: Accessible Surface Area; C: Coil; DSSP: Dictionary of Secondary Structure of Protein; H: Helix; HMM: Hidden Markov Model; HSMM: Hidden Semi Markov Model; MHMM: Modified Hidden Markov Model; MSA: Multiple Sequence Alignment; PDB: Protein Data Bank; RSA: Relative Solvant Accessibility; RMHMM: Actual RSA; PRMHMM: Predicted RSA; S: Strand
A hidden Markov model (HMM) is a statistical tool that is used to model a stochastic sequence. It corresponds to a Markov chain such that every state in the chain emits observations according to a density function. Using an HMM an observed sequence is modeled as the output of a discrete stochastic process, which is hidden. For each observation in the sequence, the process emits a symbol from a finite set of alphabets according to a probability density. HMMs are widely used in biological sequence analysis and bioinformatics. In particular, they are used in protein structure prediction studies. Hidden Markov Models first used in speech recognition problems, and typically involved mixture of Gaussian autoregressive densities which led naturally to a maximum likelihood solution of the familiar linear prediction analysis [1-4]. The first use of an HMM to predict protein secondary structure was published in 1993 [5]. A probabilistic model of protein sequencestructure relationship in terms of structural segments was proposed in [6], which formulated the question of secondary structure prediction as a general Bayesian inference problem. A Bayesian approach dealing with prior information on how to identify homogeneous segments was reported in [7]. A special type of HMM for labeled data was proposed by [8] which developed a maximum likelihood method for estimating the parameters of the model. Won et al. [9,10] applied a new method for optimizing the topology of an HMM for the secondary structure prediction using genetic algorithms. They also applied an evolutionary method to optimize the structure of an HMM. HMMs and prior biological knowledge were combined in [11,12]. The use of an HMM with a reduced set of states for predicting protein structure was considered in [13]. The EM and the Viterbi algorithms for an HMM were implemented in linear memory in [14] and a position-specific HMM to predict protein structure was described by Cheng-Li et al. [15] that combined fragment assembly, clustering, target selection, refinement and consensus in one process. To reduce the scale of the HMMs for protein secondary structure prediction, Lee et al. [16] suggested a 9-state HMM. Karplus et al. [17] introduced a new HMM based server for protein structure prediction. He provided a large number of intermediate results, which are often interesting in their own right: multiple sequence alignments (MSAs) of putative homologs, prediction of local structure features, lists of potential templates of known structure, alignments to templates and residue-residue contact predictions. Applying HMMs usually requires one to implement of the Viterbi algorithm [18,19].
Proteins are one of the most important molecules in any living cell and the study of protein structure is very important in biology. Proteins are polymer chains composed of 20 amino acids. Adjacent amino acids are connected with peptide bonds. For each amino acid, a secondary structure denotes the local spatial arrangement and the regularities of amino acids with respect to each other. Amino acids usually involve one of three main secondary structures: Helix (H), Strand(S) and Coil(C). Protein secondary structure prediction is an important problem in the field of bioinformatics, and predicting the secondary structure of a protein provides a starting point for predicting threedimensional structure, which in turn enables researchers to identify a protein structure in its entirety. Various inferential techniques, such as the nearest neighbor method, neural networks, machine learning, and methods based on information theory have been used to predict protein structure. HMMs are also well known models for the problem of predicting the secondary structure of proteins.
In a few papers on the problem of predicting protein secondary structure, high–order dependencies among emissions or the corresponding states have been considered. For example, a new probabilistic method for protein secondary structure prediction based on dynamic Bayesian networks was reported in [20]. These investigators used a multivariate Gaussian distribution and were able to account for the dependency between the profiles and secondary structures as well as the dependency between profiles of neighboring residues. In [21] a high-order HMM that permits states and observations to depend on previous states were described. Aydin et al. [22] proposed a hidden semi- Markov model that accounts for the patterns of statistically significant amino acid correlation at structural segment borders. The same paper also introduced an alternative decoding technique for the hidden semi- Markov model (HSMM). The proposed method is based on the N-best paradigm, where a set of suboptimal segmentations (the N-best list) is computed as an alternative to the most likely segmentation [23].
Some papers concerning protein structure consider the environmental features, and thereby increase the accuracy of the predicted protein structure. The Relative Solvent Accessibility, RSA, is an aspect of protein analysis that has been widely studied. Various researchers have combined RSA information with HMMs to improve the precision of the protein structure prediction [24-29].
In what follows we discuss a modified HMM (MHMM) that allows for some dependencies among emissions. In an ordinary HMM, given the state, the emissions are assumed to be independent. In the modified model that we consider, we assume each emission depends not only on the current state, but also on the previous state and on the previous emissions. We also use the RSA of an amino acid to classify each residue into one of three groups. We call this model RMHMM. Compared to the ordinary HMM, our RMHMM improves the precision of predictions. We also investigate how our proposal RMHMM changes current algorithms for ordinary HMMs.
Hidden markov models
An HMM is a stochastic process in which a hidden Markov chain of states emits a sequence of observations. A Markov chain is a sequence of random variables which has the Markov property; that is, given the present state of the process, the future and the past states are independent. In ordinary Markov chain models, the sequences of states are observable, but in hidden Markov models these same states are not observable. Suppose we have an HMM model that involves N states. These states cannot be observed, but they emit some characters (alphabets) which are observable. In what follows, we consider some dependencies among the observable emissions. It is assumed that any emission depends on one of the previous emissions. In addition, we suppose that the next emission depends on the previous state of the hidden Markov chain. We call this model a modified hidden Markov model (MHMM). Let us introduce the notation for an MHMM through the following set of four specifications:
Let St, t=1…N denote a stationary Markov chain with N states and a transition probability matrix ANXN. Let Q=q1,q2,...,qr be a sequence of T consecutive states.
Then aij, element (i,j) of A is defined by
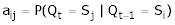
Where
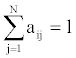
We represent observed emission of the MHMM by Yt, t=1,…,M. Suppose that the sequence Q of the states results in the observed emission 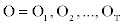 . We assume that given the emission Yk at time t-n, the state Si at time t-1 and the state Sj at time t, the probability matrix of emission Y1 at time t is denoted by
. We assume that given the emission Yk at time t-n, the state Si at time t-1 and the state Sj at time t, the probability matrix of emission Y1 at time t is denoted by
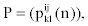
Where
Accordingly, the conditional probability distribution for an observable emission depends on the nth previous emission as well as current and previous states.
Obviously
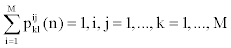
4. If we denote the initial probability distribution of state Si at time t=1 by πi , we have
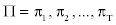
Where
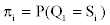
The vector of probabilities corresponding to observable emission Yk at time t=1 given state Sj at time t=1 is denoted by
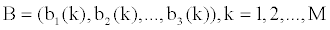
Where
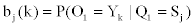
Let λ represent the entire parameter space for this MHMM.
Two of the most frequently asked questions corresponding to any Hidden Markov Model are:
Given an observed sequence of emissions from an HMM, how should we choose a corresponding sequence of states which is most probable?
Given an observed sequence of emission and the model, represented by λ, how can we calculate the probability of being in state Si at time t?
In what follows, we address these questions using our MHMM. Our goal is to show how the modified model can be constructed efficiently. In the process of applying the model to actual data, we also incorporate the information represented by RSAs of amino acids to see how these changes improve the performance of the MHMM with respect to the secondary structure prediction problem.
Finding the Most Probable State Sequence via the Viterbi Algorithm
For a given sequence of observed emission, we seek to find the most probable corresponding sequence of states. Suppose we observe the sequence
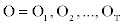
Assume that the corresponding sequence of states is
Q=q1,q2,...,qT
So we want to find 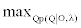 . The solution of this equation is identical to the solution of
. The solution of this equation is identical to the solution of 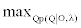 . Given the model λ, the joint probability of observed emission and state sequences is
. Given the model λ, the joint probability of observed emission and state sequences is
p(O,Q|λ) = p(O|Q,λ)p(Q|λ).
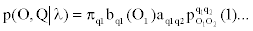
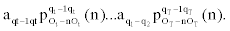
Given a sequence of observed emissions, the Viterbi algorithm computes most probable path of hidden states, see for example, [4]. In what follows we introduce a modification of the Viterbi algorithm that can accommodate the dependencies in our MHMM.
A Modified Viterbi Algorithm
Using the notation of Rabiner et al. [4], we describe the modified Viterbi algorithm via the following specification
1. Initialization:
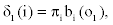
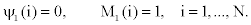
2. Recursion:
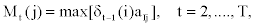
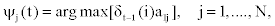
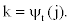
It follows that
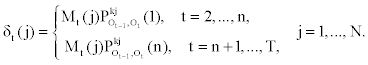
Notice that in the first part of the expression (2), the first - order dependency among observed emissions is used. This is due to the lack of sufficient observed emissions at the beginning of the sequence to use the appropriate higher - order dependency.
3. Termination:
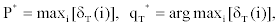
4. State sequence backtracking:
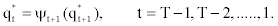
Determining the state at time t via the Forward and Backward algorithm (the posterior decoding). For a sequence of observations, 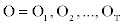 and a corresponding sequence of states, Q=q1,q2,...,qT our aim is to evaluate
and a corresponding sequence of states, Q=q1,q2,...,qT our aim is to evaluate 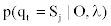 . This step is usually called posterior decoding. In what follows, we show how the ordinary method can be modified to accommodate our MHMM.
. This step is usually called posterior decoding. In what follows, we show how the ordinary method can be modified to accommodate our MHMM.
Modification of the posterior decoding
Let us define the modified forward variable by:
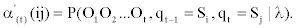
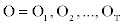 and qt given the model λ. To calculate α'(t) (ij) we proceed as follows:
and qt given the model λ. To calculate α'(t) (ij) we proceed as follows:
Where α'(t) (ij) is the joint probability of
1. Initialization:
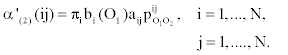
2. Induction:
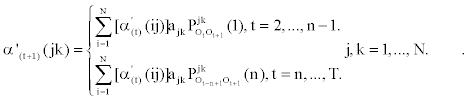
The modified backward variable β't (ij) can be defined in a similar fashion:
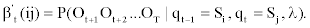
Hence we can proceeds as follows to obtain β't (ij):
1. Initialization:
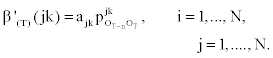
2. Induction:
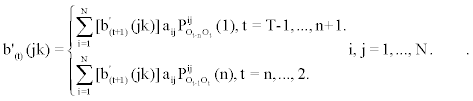
To obtain 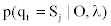 , we first calculate
, we first calculate 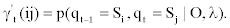
Obviously
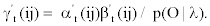
If we sum over the possible values of Si in expression (5), we obtain 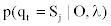 Next, we combine the MHMM with the information obtained from the RSA of each residue in a sequence of amino acids from the WHATIF dataset in the Protein Data Bank, PDB. We call the new model RSA combined with MHMM (or RMHMM).
Next, we combine the MHMM with the information obtained from the RSA of each residue in a sequence of amino acids from the WHATIF dataset in the Protein Data Bank, PDB. We call the new model RSA combined with MHMM (or RMHMM).
Dataset and the order of dependency
To analyze the performance of our model, we applied our MHMM and RMHMM to a dataset of WHATIF PDB selection list that Momen- Roknabadi et al. [27] used in their work. The dataset contains 6970 chains with resolution ≤2.5 such that identity between each pair of sequences is not more than 30 percent. We have used this dataset for both training and testing, using 5 fold cross-validation. This is briefly discussed in results and discussion. Following Aydin et al. [23], we fitted our model to the above mentioned dataset, using various order of dependencies, i.e. n=2,3,4 for helices, n=1,2 for strands and n=1 for coils. So we may have 21 types of modeling. The results show that conditioning each emission on the second previous emission, yields the best performance with respect to prediction accuracy.
Protein secondary structure
Proteins are polypeptids (polymers) of amino acids. These polymers consist of 20 different amino acids. The secondary structure of a protein is the regular structure locally defined. These spatial regularities are due to hydrogen bonds between amino acids. The secondary structures are assigned to each amino acid using the DSSP program [30]. There are eight types of secondary structures defined by DSSP: G = 310 helix; H = α -helix; I = π-helix; T = hydrogen bonded turn; E = extended strand (β-sheet) conformation; B = residue in isolated β-bridge; S = bend; and amino acid residues which do not correspond to any of the above conformations are assigned as the eighth type 'Coil'. Although, the 8-state DSSP code already represents a simplification from the 20 amino acid residues that are present in a protein, the majority of secondary structure prediction methods further simplify matters to the three dominant states: helix (H), strand (S) and coil (C). The first two are periodic motifs that are characterized by geometrical features. The coil class is the default description for all amino acids that do not belong to the helix or strand classes. In the secondary structure prediction problem, we usually assign a structural state from a threeletter alphabet consisting of {H,S,C} to each amino acid.
Solvent Accessibility and RSA Prediction
The relative solvent accessibility degree determines whether a given amino acid is external or hidden. An amino acid is declared not exposed to solvent when its observed accessibility is less than a certain fraction of its observed accessibility in a reference state. Typical values for this threshold are around 20%. We use the ASA (Accessible Surface Area) from DSSP to determine the RSA of each residue by dividing the corresponding ASA value by the maximum possible ASA for each amino acid. Momen-Roknabadi et al. [27] used some different fixed RSA thresholds for all amino acids and the residue-specific RSA thresholds. They divided amino acids into two groups (buried and exposed) and three groups, (buried, intermediate and exposed) using the RSA values. They also used different thresholds like "mean RSA" and "median RSA" for binary classification and "mean ± standard deviation" and "first tertile-second tertile" for ternary classification. Following Momen-Roknabadi et al. [27] we apply a residue specific RSA threshold approach to classify amino acids into the three groups known as buried, intermediate and exposed. According to their results, the best performance with respect to prediction accuracy is achieved when they use ternary classification, a residue dependent threshold, "mean ± standard deviation" cutoff and five-fold cross-validation. We use "mean standard deviation" of the RSA distributions as thresholds for the classification. Thus each amino acid has two cutoffs which are dependent on the mean and the standard error. Using this basis for classifying 20 types of amino acids results in 60 types of observations. We also used RVP-net [31] for predicting RSA values. The output of this program is an RSA value between 0% and 100%, which we then used to classify residues into the three classes; Buried, Intermediate, Exposed.
An accuracy measure for evaluating the prediction
In the protein secondary structure prediction problem, one of the most commonly used measures of accuracy is
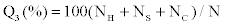
where, NH,NS and NC represent the number of correctly predicted H, S and C state, respectively, and N is the total number of amino acids. In a similar fashion, we can also define
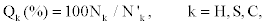
Where Nk the total number of amino acids with is correctly predicted secondary structure of type k, and N'k is the total number of amino acid of type k. The observed value of Qk represents the sensitivity of the prediction.
Modified hidden markov model
In the typical HMM, the observed emissions are assumed to be independent of each other. However in this study we first adopt a modified HMM which permits some dependencies among the emissions. We assume that the probability of observing each emission depends not only on the current state but also on the previous state and on the previous emissions. This model can be used whenever dependency among emissions should be considered. To test if this assumed dependency is reasonable, we test our modified HMM on the protein secondary structure prediction problem. To implement our modified HMM on the dataset, we used the modified Viterbi and the modified Forward-Backward algorithms that we outlined in section 2. In order to compare the fit of our model with a classical HMM, we use various measures such as Q3 and standard deviation, as well as five-fold-cross-validation [32]. Table 1 displays, Q3 the percentage of secondary structures that are correctly predicted by each model. It also indicates the percentage of helix, QH strand, QS and coil, QC type, correctly predicted by HMM and MHMM using both the Viterbi and Forward-Backward algorithms. According to these tabulated results, the Q3 criteria increases about two percent for both algorithms. The values of QH and QS also increase. Notice that, for the Forward-Backward algorithm, the value of QS is toughly 10% greater for the MHMM than for the HMM. An improvement of this magnitude is important in the protein secondary structure prediction problem. These results clearly show that using modified Viterbi and Forward-Backward algorithms yields better prediction accuracies. Our results also suggest that some dependency between conformations and their influence on the secondary structures can be captured by our modified Viterbi and Forward-Backward algorithms. Table 2 shows the prediction accuracy of each amino acid when both algorithms are used. It is intriguing to note that predictions of almost all amino acids are improved by fitting an MHMM rather than an HMM. Figures 1 and 2, respectively, show bar charts of the improvement in prediction accuracy using MHMM and HMM for each amino acid, using the Viterbi and Forward-Backward algorithms.
| Viterbi | Forward-Backward | |||||||
| Model | Q3 | QH | QS | QC | Q3 | QH | QS | QC |
| HMM | 52.28 | 59.1 | 38.85 | 55.39 | 58.05 | 67.52 | 33.52 | 65.13 |
| MHMM | 54.24 | 60.53 | 43.65 | 56.35 | 59.87 | 71.24 | 43.45 | 59.98 |
Table 1: The accuracy of the protein secondary structure prediction for HMM and MHMM using Viterbi and Forward-Backward algorithms applying 5 fold crossvalidation.
| Viterbi | Forward-Backward | |||
| Amino acid | HMM | MHMM | HMM | MHMM |
| A | 56.03 | 57.69 | 61.68 | 61.56 |
| C | 53.15 | 55.29 | 58.7 | 59.75 |
| D | 47.1 | 49.6 | 53.07 | 54.33 |
| E | 48.77 | 51.53 | 53.93 | 57.18 |
| F | 52.47 | 55.19 | 57.79 | 59.45 |
| G | 51.29 | 54.78 | 57.14 | 58.15 |
| H | 51.31 | 54.89 | 56.94 | 59.41 |
| I | 61.46 | 57.18 | 67.97 | 68.1 |
| K | 47.94 | 50.46 | 54.06 | 57.03 |
| L | 47.81 | 50.27 | 52.9 | 55.82 |
| M | 50.27 | 51.99 | 55.36 | 57.56 |
| N | 47.8 | 49.95 | 53.91 | 56.71 |
| P | 59.69 | 61.04 | 65.41 | 66.61 |
| Q | 51.43 | 53.99 | 57.91 | 59.5 |
| R | 52.04 | 54.38 | 58.32 | 59.87 |
| S | 54.59 | 56.42 | 60.36 | 62.44 |
| T | 53.64 | 55.33 | 59.8 | 63.05 |
| V | 53.64 | 55.85 | 60.01 | 60.64 |
| W | 55.35 | 57.95 | 61.25 | 62.36 |
| Y | 49.78 | 51.04 | 54.53 | 57.85 |
| TOTAL | 52.28 | 54.24 | 58.05 | 59.87 |
Table 2: The accuracy of the protein secondary structure prediction for HMM, RMHMM and PRMHMM using Viterbi and Forward-Backward algorithms applying 5 fold cross-validation.
The impact of solvent accessibility information on prediction
Environments around the protein residues can affect their propensity for different structures [28]. Therefore, amino acids may behave differently when they are located in the protein interior or on the surface. Based on this observation, other researchers have suggested that exploiting information concerning environmental factors, such as accessible surface area (ASA), might improve the prediction of secondary structures [25,27,29]. ASA is defined as the surface area of amino acid that is available to solvent. Relative solvent accessibility (RSA) is defined as the ratio of each amino acid that is accessible to solvent by dividing the corresponding ASA value to the maximum possible ASA. In this study we first derive the actual RSA from the DSSP program [30] and then use a residue - specific RSA threshold to classify each amino acid into one of three classes [27]. However, in practice we only know the sequence of the protein, and we should rely on the predicted RSA values rather than the actual values. Here we use the RVP-net predicted RSA [31]. Using the actual and predicted RSA, we develop two modified HMMs, called a Modified HMM using actual RSAs (RMHMM) and a Modified HMM using Predicted RSAs (PRMHMM), respectively. We use both the corresponding modified Viterbi and the Forward-Backward algorithms involving the actual and predicted RSA values to predict the secondary structure of proteins. Table 3 displays values of the criteria Q3 and also QH, Qs and Qc using both algorithms for RMHMM and PRMHMM, and clearly demonstrates that using the actual and the predicted RSA values improve the prediction of secondary structures. Using RMHMM, the increases in Q3 are about 4.8 % and 6% for the Viterbi and Forward- Backward algorithms, respectively. As expected, the impact of actual RSA on prediction accuracy is greater than the effect of using predicted RSA.
| Viterbi Forward-Backward | ||||||||
| Model | Q3 | QH | QS | QC | Q3 | QH | QS | QC |
| HMM | 52.28 | 59.1 | 38.85 | 55.39 | 58.05 | 67.52 | 33.52 | 65.13 |
| RMHMM | 57.07 | 58.66 | 54.6 | 59.1 | 63.95 | 67.33 | 57.3 | 67.39 |
| PRMHMM | 53.77 | 59.16 | 45.11 | 56 | 60.16 | 70.04 | 47.07 | 59.63 |
Table 3: The accuracy of the protein secondary structure prediction of each amino acid for HMM and MHMM using Viterbi and Forward-Backward algorithms applying 5 fold cross-validation.
Table 4 reports the observed prediction accuracy of each amino acid for HMM, RMHMM and PRMHMM using both the Viterbi and the Forward-Backward algorithms. In comparison with HMM, for almost all amino acids the secondary structures are predicted more accurately by both RMHMM and PRMHMM. When we use either modified model, using predicted RSAs, the observed accuracy of secondary structure predictions are lower than the corresponding values when actual RSAs are used. Figures 3 and 4 display the bar charts for prediction accuracy improvement for each amino acid in RMHMM, compared to HMM, using both the Viterbi and the Forward-Backward algorithms.
| Viterbi Forward-Backward | ||||||
| Amino acid | HMM | RMHMM | PRMHMM | HMM | RMHMM | PRMHMM |
| A | 56.03 | 56.03 | 57.69 | 61.68 | 65.93 | 62.72 |
| C | 53.15 | 54.5 | 51.71 | 58.7 | 58.62 | 60.44 |
| D | 47.1 | 57.81 | 49.92 | 53.07 | 66 | 54.12 |
| E | 48.77 | 60.56 | 51.32 | 53.93 | 66.71 | 56.72 |
| F | 52.47 | 55.98 | 54.89 | 57.79 | 61.89 | 60.17 |
| G | 51.29 | 62.98 | 54.84 | 57.14 | 68.66 | 57.99 |
| H | 51.31 | 53.36 | 54.52 | 56.94 | 61.02 | 59.46 |
| I | 61.46 | 59.93 | 57.34 | 67.97 | 66.22 | 68.1 |
| K | 47.94 | 57.63 | 50.14 | 54.06 | 64.89 | 56.27 |
| L | 47.81 | 58.52 | 49.98 | 52.9 | 64.25 | 55.86 |
| M | 50.27 | 54.49 | 51.7 | 55.36 | 63.97 | 58.04 |
| N | 47.8 | 57.52 | 48.89 | 53.91 | 64.86 | 56.38 |
| P | 59.69 | 59.99 | 60.43 | 65.41 | 68.79 | 66.47 |
| Q | 51.43 | 57.82 | 53.78 | 57.91 | 64.69 | 60.28 |
| R | 52.04 | 56.48 | 53.57 | 58.32 | 64.27 | 61.08 |
| S | 54.59 | 53.81 | 56.01 | 60.36 | 61.18 | 62.89 |
| T | 53.64 | 53.93 | 55.26 | 59.8 | 60.7 | 63.29 |
| V | 53.64 | 59.39 | 55.89 | 60.01 | 65.23 | 62.13 |
| W | 55.35 | 53.38 | 57.85 | 61.25 | 59.97 | 63.4 |
| Y | 49.78 | 53.75 | 50.36 | 54.53 | 60.03 | 57.53 |
| TOTAL | 52.28 | 57.07 | 53.77 | 58.05 | 63.95 | 60.16 |
Table 4: The accuracy of the protein secondary structure prediction of each amino acid for HMM, RMHMM and PRMHMM using Viterbi and Forward-Backward algorithms applying 5 fold cross-validation.
In general, as Tables 1-4 document, the prediction accuracy of RMHMM with respect to the goal of secondary structure prediction is superior to both HMM and MHMM. Moreover, our results suggest that corresponding both environmental information and dependency of emissions in HMM have considerable impact on the prediction accuracy of amino acid protein secondary structure. Compared to Momen-Roknabadi et al. [27], our results concerning the problem of secondary structure prediction show reasonable improvement. To test whether the difference between two values of Q3 for HMM and RMHMM is significant, we propose to use the following statistical test.
Suppose Xi is the value of Q3 for HMM, and Yi is the corresponding estimate for in RMHMM, i=1,…,k for which k is the number of iterations. We define
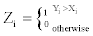
So  . The hypothesis of interest can be written as Ho : p=1/2, H1: p>1/2. If we repeat the experiment n times independently,
. The hypothesis of interest can be written as Ho : p=1/2, H1: p>1/2. If we repeat the experiment n times independently, 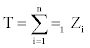 (i.e. the number of times that Yi exceeds Xi)
(i.e. the number of times that Yi exceeds Xi)
is a random variable with a binomial distribution. Using the Neyman- Pearson test, for the significance level α=0.1, n=5 (as already mentioned, we used five-fold cross-validation) and p=1/2, the test statistic becomes
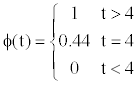
If we suppose that Yi is the value of Q3 for RMHMM, we can use this test to determine whether the improvement for RMHMM is significant. The results show that in all five iterations, the Q3 scores for both the MHMM and RMHMM are significantly greater than those for HMM. (See the additional files, which also contain information about QH, QS and QC).
Considering dependency among emissions seems reasonable and leads to some improvement in the prediction accuracy of protein secondary structure. Similarly, using RSA information will also result in improved prediction. So, combining RSA information with various dependency features in HMMs can be used in various hidden Markov models to improve the accuracy of predicting the protein secondary structure.
Hamid Pezeshk would like to thank the Department of Research Affairs of the University of Tehran. Sima Naghizadeh and Vahid Rezaeitabar are grateful to the Department of Statistics at Tarbiat Modares University. The authors would like to thank Mr. Amir Momen-Roknabadi for providing the dataset and Miss Nasim Ejlali for helpful comments on an earlier draft of this paper. Some parts of this work were carried out when Hamid Pezeshk was visiting department of statistics at Waterloo, Canada.