Journal of Theoretical & Computational Science
Open Access
ISSN: 2376-130X
ISSN: 2376-130X
Research - (2024)Volume 10, Issue 3
The Infrastructure as a Service (IaaS) cloud computing service model facilitates on-demand sharing of computing resources over the internet. The scheduling of these resources is the main dispute that has to be handled. Recently, different swarm-based algorithms have been implemented for scheduling. The main intention of the cloud scheduling problem is to satisfy user requirements by allocating resources. This paper proposed a two-phase task scheduling algorithm named Clustered Input Oriented Salp Swarm Algorithm (CIOSSA). In the first phase, named Task Splitting Agglomerative Clustering (TSAC), the tasks are categorized based on the deadline and the output generated by TSAC becomes the input to the next phase. The Input Oriented Salp Swarm Algorithm (IOSSA) is used for the scheduling process. It is a multi-objective version of the fundamental Salp Swarm Algorithm (SSA) which experience slow convergence rate. Here a fundamental version SSA is proposed with two different objectives satisfied by two separate leaders. The use of two leaders instead of one expands the search space of the optimization problem. This proposed algorithm achieved efficient utilization of resources, which in turn reduced the cost. It also improves the schedule make span. The experimental analysis is performed in cloudsim. The simulation result shows that the proposed CIOSSA framework will produce better results than the existing algorithm.
Cloud computing; Clustering; Resource allocation; Scheduling; Swam algorithms
Cloud computing makes possible the on-demand accessing of cloud computing resources like disk space, virtual Central Processing Units (vCPU), Random Access Memory (RAM), etc. over the internet. These resources are in the outline of a virtual machine and are deployed in physical machines. Three trendy service models in cloud computing are Platform as a Service (PaaS), Software as a Service (SaaS) and Infrastructure as a Service (IaaS). The IaaS service quality and cost of cloud computing are standing on the resource allocation process and the resource provider [1].
The allocation of resources to customers should be optimal. Different resource management strategies like the centralized model, hierarchical model can be used for the efficient allocation of resources [2]. Clustering is the method of dividing data points into different groups. Clustering is classified as hierarchical clustering and partial clustering. Hierarchical is subdivided into agglomerative and divisive [3-5].
One of the main disputes to handle carefully in cloud computing is task scheduling and will affect the performance of resource allocation in clusters of the cloud environment. The chief goal is to decrease the makespan of schedule that will cause the efficient utilization of resources. The second objective is to reduce costs. Scheduling is an optimization problem and is a Nondeterministic Polynomial (NP) time hard problem. Nearly optimal solutions are obtained for optimization problems by the introduction of heuristic algorithms.
Simplifier Swarm Optimization (SSO), Particle Swarm Optimization (PSO) and Mean Grey Wolf Optimization (MGWO) algorithm, Salp Swarm Algorithm (SSA), etc. are swarm intelligence algorithms. These meta-heuristic swarm-based algorithms will give a near-optimal schedule that will attain the above-mentioned objectives [6-15].
Some existing methodologies proposed for resource allocation are Kumar et al., presented a swarm-grounded meta-heuristic method called Generalized Ant Colony Optimizer (GACO) [16]. This fusion method comprised of easy ant colony optimization and global colony optimization idea.
Malekloo et al., proposed Multi-objective ACO (MACO) method for Virtual Machine (VM) assignment with consolidation [17]. This method attains a trade-off among system performance, energy efficiency, along with Service Level Agreement (SLA)-compliance. Abdel-Basset et al., centers on VM assignment issue regarding to the obtainable bandwidth that is equated as changeable sized bin stuffing issue [18]. Furthermore, a bandwidth allotment plan is introduced and fused with an enhanced alternative of Whale Optimization Algorithm (WOA).
The task scheduling algorithm grounded on bacterial foraging optimization to lessen the inoperative time of VMs while the load balancing along with runtime minimization have arised [19]. Saleh et al., gave the Improved Particle Swarm Optimization (IPSO) algorithm to offer the most favorable allotment for a great task count [20]. This is attained by dividing the suggested tasks into batches in a vibrant way. The resources utilization situation is measured in all construction of batches.
Patel et al., focused on reducing on the whole makespan with useful load balancing via forming the swarm intellect of social spider by messy inertia weight grounded arbitrary assortment [21]. The projected algorithm stops the local convergence plus investigates the worldwide intelligent penetrating in deciding the finest optimized VM for the user mission.
Rana et al., proved a meta-heuristic approach to attain optimal results. In a heterogeneous atmosphere, where millions of resources can be owed and deallocate in a part of time, current metaheuristic algorithms execute fine owing to its vast power [22]. Here a theoretical structure for solve multi-objective VM scheduling issue was presented by meta-heuristic WOA. Haghighi et al., by virtualization method provided a fusion method for resource administration [23]. This method exploited k-means clustering for mapping job as well as active consolidation process, enhanced through micro-genetic algorithm.
Gawali et al., discussed about task scheduling and resource allocation [24]. A heuristic method was proposed to carry out task scheduling and resource allotment. Gawali et al., gave a Standard Deviation rooted Modified Cuckoo Optimization Algorithm (SDMCOA) for scheduling the tasks with two phases [25]. In the primary phase, the sample preliminary populations were estimated among the accessible count of task’s population.
The proposed task scheduling algorithm is titled as CIOSSA. The basic framework followed is hierarchical modeling. The following are the key goals of CIOSSA:
• The proper utilization of resources that scales down the wastage of computing power by checking the resource availability at the time of scheduling.
• A preprocessing clustering mechanism has been introduced to give priority to tasks based on the current resources.
• The scheduling is based on resource requirements and the priority of tasks, so the First in First out (FIFO) ordering scheme is changed.
• An improved version of SSA is recommended in this paper, which makes use of two separate leaders.
The proposed method follows a hierarchical modeling approach with some modifications. It also uses the hierarchical clustering method for task categorization and a modified SSA for scheduling.
Hierarchical modeling approach
In the hierarchical modeling approach, the resource allocation and management are maintained master-slave structure. The master manages users to request and resources. The VMs are managed at a cluster level. The VMs are deployed in Physical Machines (PM). The virtual resources allocation is done at the VM level [4]. The basic diagrammatic representation is shown in Figure 1.
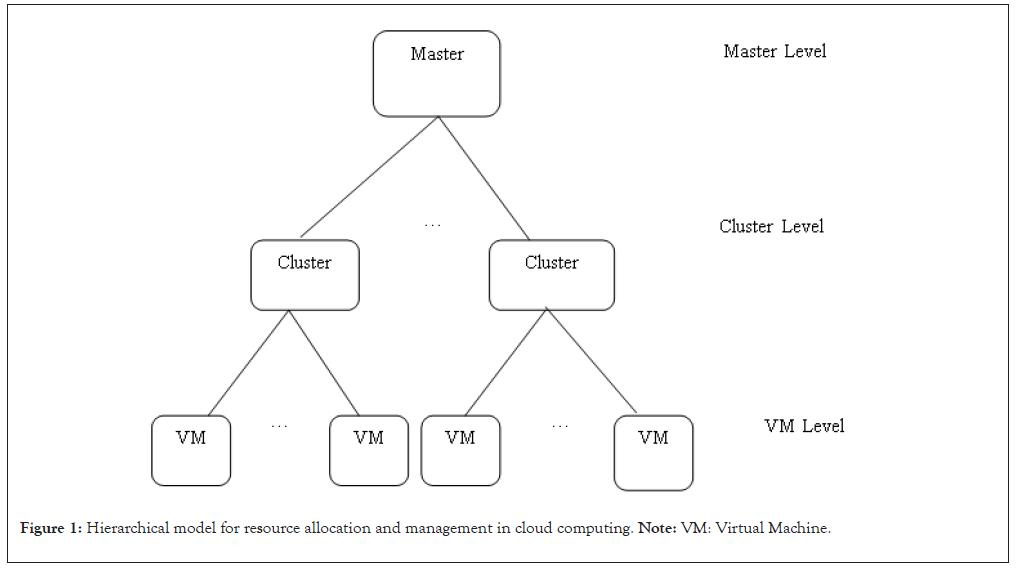
Figure 1: Hierarchical model for resource allocation and management in cloud computing. Note: VM: Virtual Machine.
The PMs that are involved in cloud computing services are categorized as hot, warm and cold. Hot systems are those having active VMs able to run jobs at this moment, warm means VMs are running not able to run the job at this moment and cold means the VMs are turned off. The cold state requires more time to turn to active mode as compared to warm.
The existing hierarchical model has some shortcomings [1]. Here considering only one of the active PM states, the PMs may be in other states. The scheduling policy used here is FIFO during the time of scheduling jobs.
The availability of the required amount of resources is not checked during the allocation job. During the execution time, only the deficiency of resources is understood.
All tasks in the job are allocated to a single PM. The resource pool contains a set of PMs, each PMs contains some free VMs. Suppose a new job comes, sufficient VMs for executing that job are distributed in different PMs, not in a single PM so the allocation is not possible the job has to wait.
Hierarchical clustering
The hierarchical clustering separating data points into different groups based on the same measure of similarity. Initially, each data point is a cluster of its own. Then find out the least distance between two clusters and bring them together. This is represented in a tree-like structure called dendrogram we terminated when we are left with one cluster. The key steps in hierarchical clustering are:
• Measure the similarity distance between different data points.
• Grouping or combine the nearest clusters.
• Stop grouping until termination criteria reached.
In this method, the data points are distributed over Euclidean space and Euclidean distance measure is used to measure the distance between clusters.
Salp swarm algorithm
SSA is a nature stimulated algorithm and imitates the behavior of salp in oceans or seas. Their food source identification is a group activity and forms a salp chain. The chain contains a leader at the front and others are followers. The followers will change their position based on the inspiration from the leader. In general, the possible solutions mean population serves as the salp chain the position of the best solution in the population is denoted as the food source position (F) in the chain denotes the best solution for the problem. Each solution has n-dimensions, where n is the count of problem variables. Two-dimensional matrix is used to store the position of all salps, which is the x and y coordinates. This concept can be mapped into scheduling problems and Mirjalili et al., tested SSA on several mathematical optimization functions and observe that SSA is an effective approach for scheduling problems [10].
The main fault identified during the analysis of SSA concerning cloud scheduling problems is the slow convergence rate. The goal of searching ability is also minimized.
Problem description
The SSA is good enough for cloud scheduling problems [11]. A resource allocation algorithm named Clustered Input Oriented Salp Swarm Algorithm (CIOSSA) based on SSA is proposed. It minimizes makespan, which in turn reduces resource utilization and the cost of resources. In this model, independent and heterogeneous jobs are considered for scheduling. A heterogeneous workload means the jobs are requesting different amounts of resources, and more than one job is in the PM's waiting queue.
Basic architecture
Cloud computing makes possible the on-demand accessing of cloud computing resources like disk space, vCPU, RAM, etc. These resources correspond to virtual machines they are deployed in physical machines. The Cloud Service Providers (CSP) are availing the cloud computing services to customers as their request. The IaaS service quality and cost of cloud computing are based on the resource allocation process and the resource provider. The allocation of resources to customers should be optimal.
The main intention of the cloud scheduling problem is to satisfy user requirements by fruitfully allocating resources. The final solution schedule is optimal or near-optimal. The customer's request represented as heterogeneous tasks T = {T1,T2,T3,...Tn}. These tasks carried out by the allocation of VMs, say VM = {VM1,VM2,VM3,...VMm}. The chief goal of the proposed framework is to create a resource allocation algorithm in the cloud environment. The proposed resource allocation algorithm named CIOSSA provides efficient utilization of resources and reduces the cost.
The architecture of the proposed method is verified in Figure 2. It is modeled as entry part, clustering phase and optimization phase. The task is entered into the task entry stage. The clustering stage considers the tasks in the entry queue and categorizes them into low range and high range tasks. The deadline is the margin for this categorization and is described in task entry (Figure 2).
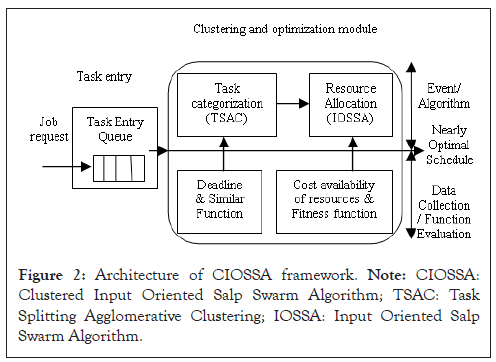
Figure 2: Architecture of CIOSSA framework. Note: CIOSSA: Clustered Input Oriented Salp Swarm Algorithm; TSAC: Task Splitting Agglomerative Clustering; IOSSA: Input Oriented Salp Swarm Algorithm.
In the proposed framework the clustering scheme is the variation of hierarchical agglomerative clustering named Task Splitting Agglomerative Clustering (TSAC). Though several existing works are identified the greatest intention of this stage is to identify the task's urgency. In other words, this stage gives some way of priority to tasks based on the deadline. This will change the First Come First Serve Scheduling (FCFS) policy of task execution.
Optimization is the next important stage in the framework. It is obtained by using the improved SSA called IOSSA. It is one of the swarm-based techniques that incorporate the objective function during task scheduling. At the time of resource allocation, the resource availability is checked across the user requirement efficiently than existing schemes.
TSAC explains the classification of tasks from the task entry phase by incorporating clustering. The categorized tasks from the clustering phase are taken as input by the optimization stage that is described detailed in IOSSA.
Problem formulation
The chief principle of the proposed method is to create a task scheduling algorithm in the cloud environment. The main objectives during the implementation are makespan and cost. Optimal task scheduling will be the one that optimizes the make span of the schedule S. Makespan is termed as the quantity of time from start to finish for carrying out a set of jobs i.e. it is the utmost completion time of every jobs. The main objective of the proposed framework is formulated using Equations (1-3):
Obj(S) = μ ✕ Obj1(S) + (1-μ) ✕ Obj2(S) ……. (1)
Where, 0<μ<1
Obj1(S) = min(Makespan(S)) ……. (2)
Makespan(S) = max Σi=1,2,,m (VMi (CTTj)) - min Σi=1,2,,m (VMi (STTj)) ……. (3)
Where, CTTj is the task completion time and STTj is the start time of task. The variables that are used in this paper are defined in Table 1. The parameters under consideration during the scheduling comprise vCPU cost and requirement of memory and its cost. The cost is computed using Equations (4-7).
| Variables | Description |
|---|---|
| Ti Tj | Cluster of tasks |
| Dtx | Deadline of tasks tx in Ti |
| Dty | Deadline of tasks ty in Tj |
| Totalcost | Total cost |
| vCPU | Need of virtual Central Processing Unit |
| Memneed | Need memory |
| TotvCPUcost, TotMemcost | Total vCPU and Memory cost |
| vCPUcost, Memcost | vCPU and Memory cost |
| ReqMem, ReqvCPU | Required vCPU and Memory |
| KC | TEQ waiting buffer size |
| TEQfront & TEQrear | Points to front and rear ends of Task Entry Queue (TEQ) |
| t | Current iteration |
| lb[] | Lower bound |
| ub[] | Upper bound |
| Xj | Position of salp |
| Fj | Position of food source |
| N | Population/number of tasks |
| Ibest | Best solution of each iteration |
| Nreq | Maximum iterations/total number of requests |
Table 1: Variable description.
Obj2(S) = min(Totalcost) ……. (4)
Totalcost = f (TotvCPUcost TotMemcost) ……. (5)
TotvCPUcost = (ReqvCPU ✕ vCPUcost) ……. (6)
TotMemcost = (ReqMem ✕ Memcost) ……. (7)
The low-cost tasks earn more priority, which may cause missing of the deadline by some other tasks. In the proposed method a task classification is introduced in terms of deadline, to cope with that deadline constraint.
Proposed model
The proposed model span comprises three main stages such as task entry, clustering and optimization. Initially the proposed framework changes the existing FIFO task selection. Further, during customer resource allocation the current resources availability are checked dynamically. Again it fuses a multi-leader SSA for the creation of an optimal schedule.
Task entry
The main entity in the task entry segment is the Task Entry Queue (TEQ). When a user request a resource that is a new task has entered the status of the TEQ is checked, if it is full the newly entered task is dropped. Otherwise, it is added to the queue. The pseudo-code representation of the task entry-stage is depicted in algorithm 1.
Algorithm 1-Task entry:
Input : Enter job into TEQ with maximum buffer size in KC
Output : Allot job in the queue
TEQ is the array representation of Queue structure with TEQfront and TEQrear points front and rear ends.
Algorithm Task Entry (Job)
{
TEQfront=0, TEQrear=-1;
While (TEQfront ≤ KC-1)
TEQrear ++;
KC ++;
Enqueue (Job)
End while
TEQ is full and Drop Job.
}
Task Splitting Agglomerative Clustering (TSAC)
The proposed clustering system is named as Task Splitting Agglomerative Clustering (TSAC) because the task categorization is taking place in clustering. To the best of our knowledge, this is one of the best categorization methods using the clustering concept. Consider there are 10 different tasks T1, T2-T10 is in TEQ and they are entered in the order of T1 first, T2 second and so on. Their deadlines are 93, 78, 10, 67, 81, 89, 21, 34, 9, 26 milliseconds respectively. The tasks having deadline 93, 78, 67, 81, 89 say T1,T2,T4,T5,T6 are in low priority category and tasks having deadline 10, 21, 34, 9, 26 that is T3,T7,T8,T9,T10 are in high priority category. Suppose the tasks in category one is selected for scheduling T1,T2,T4,T5,T6 are scheduled first. This changes the default scheduling policy FIFO of the hierarchical modeling approach.
In the TSAC system initially, each task becomes a cluster. Distance between clusters Ti and Tj is the minimum distance between any object in Ti and Tj. The distance measure is based on the deadline of tasks. The mathematical model for similarity calculation is using Equation (8).
where txεTi and txεTj ……. (8)
Merge clusters based on maximum similarity.
Algorithm 2-Task Splitting Agglomerative Clustering (TSAC):
Input: Tasks to be scheduled.
Output: Two clusters, high range and low range
Initially each task makes a cluster search space.
Set CL as total number of clusters.
Evaluate Max sim(Dtx ,Dty )
While (CL ≤ 2):
Merge the two closest clusters
Update Sim (Ti, Tj)
Decrement CL by 1
End while
Input Oriented Salp Swarm Algorithm (IOSSA)
Here in the proposed framework, a variation of SSA named IOSSA is used for the optimization process. In the traditional SSA, goal searching is performed based on a single leader that may cause a reduction in performance. Two separate leaders having two different objectives are introduced in the proposed work. This multi-objective algorithm earns a full extension of search space. It helps to find the optimal schedule. This in turn, improves resource utilization, cost, makespan, etc.
The first step of the SSA algorithm is to set the initial population since the original population is very large. Generally, the initial population is taken as a random selection procedure. In the proposed work the tasks are categorized based on priority. Based on this prioritized schedule the proposed TSAC algorithm identifies the customer requirements rather than random selection. The resource availability is checked against the resource pool. The resources are allocated when the resource pool has sufficient resources. If not, tasks are distributed over the available VMs.
One of the main overhead that has to be handled in this proposed method during the initial stage is the selection of the task category. Based on the availability of resources, measures in terms of vCPU, memory and cost, the high range or low range tasks are selected for the scheduling. This results in the avoidance of resource overloading. If the availability of resources is higher, the high range tasks are advised for scheduling. If VMs are already busy then low range tasks having a low deadline, have to be completed very fast and are selected for scheduling. That means the most important tasks are treated and will get more priority.
The scheduling process comprises two-step processes. The first step is the allocation of VM and is known as resource allocation. The next step is the assignment of the time slot to tasks in the selected VM named task scheduling. One of the main considerations in the SSA is the selection of the number of iteration, here in IOSSA it is based on the tasks count. As the tasks count increased the count of possible schedules is also increased.
Algorithm 3-Input Oriented Salp Swarm Optimization (IOSSA):
Input: Tasks to be scheduled
Output: Nearly optimal schedule
Initilaize the population based on number of task n.
Initialize maximum iterations based on total number of request.
Set upper bound (ub1 and ub2) and lower bound (lb1 and lb2). Initialize (C1, C2 and C3) using random function.
Set the initial iteration t=1.
Generate the initial populations.
• Categorize the tasks using TSAC Algorithm.
• Availability of resource is checked and select task category.
• Select the task category based on TSAC.
• Identify individual items in population (m!/2).
While, (t<max (t))
Evaluate two fitness values for each schedule using fitness function Obj1 and Obj2.
Identify the best solution F1 for Obj1 and Obj2.
Set k as 1 to handle each objects in initial population.
Update C1.
k=1
for no item in the population remains to visit
If (k==1)
Update position of leader1 and leader2.
else
Update position of follower of Obj1 and Obj2
End for
Increment t by 1
Update lower and upper limits.
End while
Identify the best out of two.
Return best solution
The makespan and scheduled total cost is thus minimized by the proposed IOSSA. The follower tends to change their location according to a sole leaders salp in existing SSA that cause performance reduction. Therefore the proposed IOSSA utilizes two salp chains having separate leaders. Among them one salp chain i.e., Obj1 (S) takes care on makespan and the other salp chain Obj2 (S) reduces the total cost. From these two salp chains the best solution is constructed by Equation 1. Though SSA is employed to solve complex optimization issues in some cases sub-optimal solution is obtained due to lack of global searching ability. But due to two salp chains utilization, this issue is resolved.
Mathematical model for IOSSA
For the mathematical representation, each object in a population that is the schedules is divided in two groups: leader and followers. The leader changes their position based on the requirement of Central processing Unit (CPU) and memory. The leader updates the position using Equation (9).

Where, Sol[1] represents the position of leader salp, Fk is the food position, ub[k] indicates the kth dimension upper bound and lb[k] is kth dimension lower bound; C1,C2 and C3 are coefficients and are random numbers. The parameter C1 handles exploration and exploitation and is calculated using Equation (10).
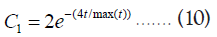
Where, t is the current iteration as well as max(t) is the maximum iteration count. C2 also C3 are a random number in the range [0, 1].
At first the leader position is updated using equation 9 and according to the position of leader, the followers are updated using Equation (11).

Where, t ≥ 2 and Sol[k] indicates the position of kth follower. The proposed IOSSA is illustrated in Algorithm 3.
The evaluation matrices considered in this paper include cost, resource utilization, makespan with time and memory usage. Makespan is calculated using Equation (12), and is related to the task start time (i) and task completion time (j).

Resource exploitation is the handling of shareable resources like memory and vCPU. It is determined by Equation (13).
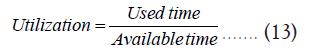
Superior resource utilization makes confident that resource idle time is less. The cost value is computed in terms of vCPU and memory needed as in Equation (14).
cost = vCPUNeed + MemNeed ……. (14)
The CIOSSA cost evaluation findings are gathered and a graph is made during the result exploratory phase. Then the proposed system makespan is compared with existing algorithms Genetic Algorithm (GA), PSO, Gray Wolf Optimization (GWO) and a freshly announced container base GWO. Finally, in terms of makespan, resource utilization, cost and memory, the CIOSSA is compared with traditional SSA.
Experimental setup
The simulation result analysis is done on HP PC with intel CORE i5 8th Gen x64 based processor having 1.60 GHz–1.80 GHz processing speed and 8 GB of RAM. The proposed framework performance is assessed by CloudSim simulator. The CloudSim 4.0 toolkit is run on windows 10 platform NetBeans IDE 8.2 as IDE and it is associated with jdk 1.8.0_111 jdk package.
In our proposed model the capabilities of VMs such as available memory, the processing speed of VCPU are variant. To evaluate Clustered IOSSA (CIOSSA) several tasks are managed with various sets of tasks and VMs. Here the tasks and VMs are heterogeneous.
Evaluation of results
The cost function of CIOSSA is measured against varying a number of tasks. The cost value is calculated on the dynamic resources availability and the individual cost of resources. It is fluctuating in nature and is tabulated in Table 2. The simulation environment has 30 Physical Machines, 86 VMs distributer over this PMs and a totally of 166 vCPUs (Table 2).
| Number of tasks | cost ($) | Number of tasks | cost ($) |
|---|---|---|---|
| 50 | 325 | 200 | 461 |
| 80 | 495 | 300 | 316 |
| 100 | 533 | 400 | 206 |
Table 2: Cost evaluation.
As per the cost analysis, if the number of tasks is less than 100, more resources are present and the idle time of resources increases, thereby boosting the cost value. As the number of jobs grows and we need to fit them into existing resources, there appears to be a higher requirement for task distribution across different VMs. As the number of tasks increases, the cost value will decrease.
The simulation environment has 30 Physical Machines, 86 VMs distributer over this PMs and a totally of 166 vCPUs. One of the widely used software development systems introduced recently is a micro-service system. It comes up with a two-layer resource structure having container or Operating System (OS-level) and VM level. Dimple et al., introduces a Grey Wolf Optimizer (GWO) in the containerized cloud [21]. The proposed system results are compared with this newly arrived elastic scheduling micro-service system and it is shown in Figure 3. The results are taken by the assumption that there are 50 containers or 50 active VMs. The proposed system and the two-layer system give almost similar results for makespan (Figure 3).
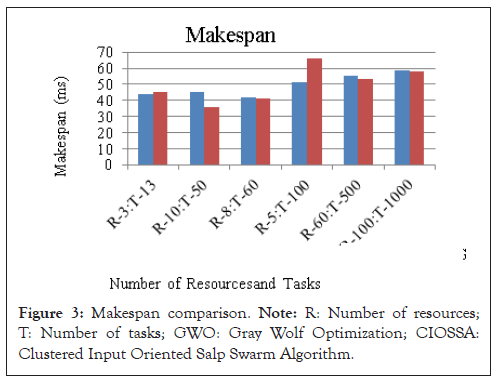
Figure 3: Makespan comparison. Note: R: Number of resources; T: Number of tasks; GWO: Gray Wolf Optimization; CIOSSA: Clustered Input Oriented Salp Swarm Algorithm.
The comparison of traditional algorithms and proposed CIOSSA in terms of different performance metrics. The X-axis represented the tasks count along with availability of resources while the y-axis parameter is varied as makespan, resource utilization, cost and memory usage. Figure 4, depicts the performance evaluation of the GA, PSO, GWO, SSA and proposed algorithm CIOSSA in terms of makespan for 85 VMs distributed among 30 PMs [9-11]. If there are 13 tasks and 3 resources available, the GA, PSO, GWO, SSA and CIOSSA makespan values are 24.05, 22.11, 20.12, 19.35 and 18.12. When the tasks count is 30 and the resources count is 30, the makespan values are 785.42, 774.46, 761.54, 755.43 and 744.48. Hence it is observed that the makespan of CIOSSA is lower as compared to other existing algorithms. Thus the resource utilization is increased automatically as the reduction in makespan is observed. The proposed framework produces a 3% improvement in makespan as compared to SSA. It is also noticed, as the number of available resources increased, the makespan got reduced (Figures 4 and 5).
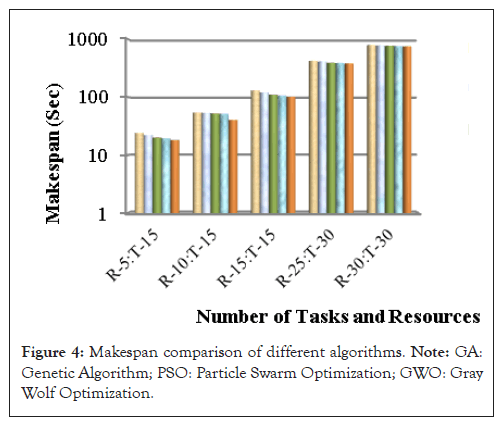
Figure 4: Makespan comparison of different algorithms. Note: GA: Genetic Algorithm; PSO: Particle Swarm Optimization; GWO: Gray Wolf Optimization.
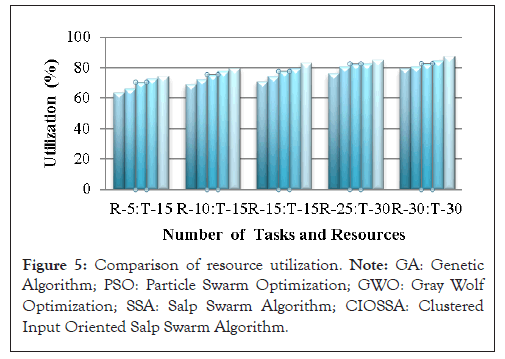
Figure 5: Comparison of resource utilization. Note: GA: Genetic Algorithm; PSO: Particle Swarm Optimization; GWO: Gray Wolf Optimization; SSA: Salp Swarm Algorithm; CIOSSA: Clustered Input Oriented Salp Swarm Algorithm.
It is thus observed around a 3% improvement in resource utilization in proposed framework is observed. The cost and memory usage of GA, PSO, GWO, SSA and CIOSSA could see in Figures 6 and 7.
The cost value is based on the dynamic availability of resources as well as their individual costs. 564,624,653,574 and 551 are the total costs observed for various algorithms and is shown in Figure 6. According to the results of the experiment, GA, SSA and CIOSSA all had improved cost results, with CIOSSA being the best (Table 3 and Figure 6).
| Resources and tasks | Cost ($) | Memory (MB) | ||
|---|---|---|---|---|
| SSA | CIOSSA | SSA | CIOSSA | |
| R-5:T-15 | 12.6 | 9.38 | 100555 | 96445 |
| R-10:T-15 | 30.3 | 12.4 | 112545 | 100542 |
| R-15:T-15 | 42.3 | 21.7 | 135486 | 114493 |
| R-20:T-30 | 134 | 87.3 | 165688 | 145485 |
| R-25:T-30 | 178 | 137 | 175469 | 156954 |
| R-30:T-30 | 206 | 158 | 196354 | 168405 |
Note: SSA: Salp Swarm Algorithm; CIOSSA: Clustered Input Oriented Salp Swarm Algorithm; R: Number of resources; T: Number of tasks.
Table 3: Comparison for cost and memory.
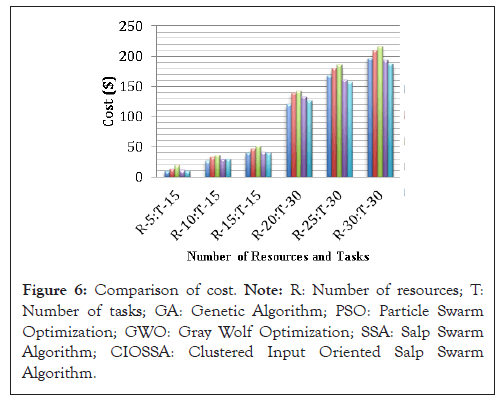
Figure 6: Comparison of cost. Note: R: Number of resources; T: Number of tasks; GA: Genetic Algorithm; PSO: Particle Swarm Optimization; GWO: Gray Wolf Optimization; SSA: Salp Swarm Algorithm; CIOSSA: Clustered Input Oriented Salp Swarm Algorithm.
Here, R refers to the resources count and T refers to the task count. The cost and memory are also noticed for increasing tasks and resources for the proposed algorithm and with existing SSA algorithm. The memory is measured in MegaBytes (MB). This proves that the proposed algorithm offers better resources with low memory utilization. This thus states the efficiency of the proposed algorithm (Figure 7).
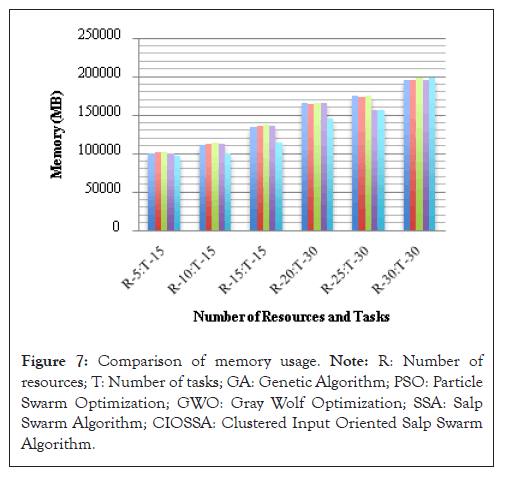
Figure 7: Comparison of memory usage. Note: R: Number of resources; T: Number of tasks; GA: Genetic Algorithm; PSO: Particle Swarm Optimization; GWO: Gray Wolf Optimization; SSA: Salp Swarm Algorithm; CIOSSA: Clustered Input Oriented Salp Swarm Algorithm.
The average memory utilization of compared methods is 147335.67, 147492.67, 149286.17, 144399.50 and 135387.33 respectively. This indicates that the proposed technique provides more resources while using less memory. As a result, the proposed algorithm's efficiency is stated.
The purpose of the proposed method is to minimize cost and makespan. It's also linked to a constant μ, whose value ranges from 0 to 1. When it gets close to 0, makespan gets more weight and when it gets close to 1, the cost value gets more weight. When the value is somewhere in the middle of 0 and 1, both makespan and cost are equally important.
In this paper, a resource allocation algorithm named clustered input oriented salp swarm algorithm modeled in a hierarchical modeling approach. In the proposed model, a clustering mechanism has applied to change the FIFO structure execution of tasks. The analysis of the proposed model is done rooted on the performance metrices like cost evaluation, memory, makespan and resource utilization. The analysis given concluded that the proposed CIOSSA framework has improvements in resource utilization cost and memory usage. The proposed framework produces a 5% improvement in makespan and around a 10% improvement in resource utilization as compared to existing SSA. Future research projects will focus on crucial elements like load balance and flow time when scheduling tasks and jobs. Additionally, while the findings were only tested on CloudSim, they were later confirmed in real-world settings.
Citation: Murali AJ, Brindha T (2024). A Multi-Objective Clustered Input Oriented Salp Swarm Algorithm in Cloud Computing. J Theor Comput Sci. 10:225.
Received: 12-Aug-2024, Manuscript No. JTCO-24-33472 ; Editor assigned: 14-Aug-2024, Pre QC No. JTCO-24-33472 (PQ); Reviewed: 28-Aug-2024, QC No. JTCO-24-33472 ; Revised: 04-Sep-2024, Manuscript No. JTCO-24-33472 (R); Published: 11-Sep-2024 , DOI: 10.35248/2376-130X.24.10.225
Copyright: © 2024 Murali AJ, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.