Clinical & Experimental Cardiology
Open Access
ISSN: 2155-9880
ISSN: 2155-9880
Research Article - (2016) Volume 7, Issue 9
Cardiac performance measurements of the isolated beating heart are essential for the evaluation of new pharmaceutical heart treatments. In the small animal, the means for these measurements usually are direct pressure changes in the left ventricle. Although volume equations are also used, they usually are indirect correlates of the pressure changes as opposed to true anatomical or dimensional measurements. In order to acquire detailed cardiac physiological data echocardiographic studies have been used in alive small animals. However, these are experimental techniques that demand a high level of expertise and expensive equipment.
A new easy to use and fast charge-coupled device (CCD) analysis tool has been developed by our team for the isolated beating heart, based on morphometric changes of the projected heart‘s surface. It uses a commercially available fast CCD camera technology, home-made software and an image acquisition-analysis method to extract true dimensional changes. Its significance relies on acquisition and assessment of the cardiac anatomical parameters, using non-contact methods.
A high definition CCD camera is used to acquire images from the isolated beating heart. Subsequently, image analysis software is used to eliminate noise and provide morphometric data (heart chamber dimensional changes) which are transformed to myocardial contractility indices and heart rate measurements.
In conclusion, the new method presented in this paper is contactless, unbiased, cost effective, simple and can be used to evaluate the cardiac function in an ex vivo working model.
Keywords: Langendorff; Ischemic heart; Dimensional changes; Cardiac performance; Evaluation
The ex vivo heart perfusion model is a well-accepted preparation, introduced more than a century ago. Nowadays, it is not so much used in the study of heart’s physiological principles, but in supplying corresponding physiological evidence to underlying molecular processes of ischemia, altered myocardial metabolism, new pharmaceutical agents, etc., [1].
Although it was named after Oscar Langendorff who demonstrated its use in the mammalian heart in 1895, the same model was well established by Elias Cyon in the frog heart as early as 1866 [2,3]. The chronological reference to the origin of the method is important not only for historical reference reasons, but also, and particularly so, for highlighting the tremendous efforts of the early physiologists to develop suitable recording methods in parallel. Although the continuous pressure monitoring was achieved quite early, almost simultaneously with the genesis of the model, the morphometric assessment of the beating heart, by means of volumetric changes, diastolic and systolic changes, was not possible until much later, during Starling’s era. The Nobel prize honored Ernest Starling not only for depicting the famous volumepressure relationship, but mainly for his outstanding originality to place the large animal heart in an hermetically closed brass cardiometer [1,4] and achieve for the first time the end diastolic volumetric recording of the left ventricle, by combining valves, stopcocks and manometers. To understand the value of his monitoring method, we need to consider that the morphometric diastolic and systolic monitoring of the left ventricle remains challenging even today that state-of-the-art pressure sensors and recording methods are used. In a working model, where the perfusate follows a physiological route, the ventricular performance (pressure and volume) can be directly monitored, only if the heart is big enough to accommodate a sensor without a valvular leak. In a small heart, working preparation (rat, mouse, rabbit), the left ventricular pressure and volume measurements can only be indirect, as originally used by Joseph Coats, i.e. through regulation of ventricular input and measurement of pressure output in the aorta. In a non-working model, where the left ventricle pumps empty, the volume monitoring is impossible, whereas the pressure monitoring cannot be direct. The only solution is to monitor isovolumetrically the left ventricular pressure through a water filled balloon in the ventricle. The left ventricle squeezes the balloon during systole and this is transmitted to a pressure sensor which reflects the pressure wave on the screen.
Although the latter method is one of the most widely used, it poses certain understandable limitations, as the shape and size of the balloon induces a certain degree of subendocardial ischaemia. In addition, the isovolumetric fixation of the left ventricle to a predetermined volume makes the volumetric changes of the left ventricle impossible to assess, being biased by an inflated balloon fixed in the left ventricle. Overall, there is no current contactless method to assess the systolic and diastolic morphometric changes of the ex vivo beating heart, especially of the small animal.
In this article we present a new method that ensures accuracy, simplicity, cost effectiveness and unbiased monitoring of the ventricular performance. More specifically, the projected surface of the heart is measured directly and the most sensitive and specific morphometric parameters are used to evaluate the systolic and diastolic cardiac function on the ex vivo rabbit heart.
Surgical procedure and heart perfusion
Animal treatment was in compliance with Patras Medical School Policy on Animal Experimentation and all procedures were carried out in the most humane way possible. The study was performed on six New Zealand white rabbits, of either sex, 2-5 months of age, weighing 2-3.2 Kg. The rabbits were anesthetized with a mixture of intramuscular ketamine (50 mg/kg) and xylazine (10 mg/kg) to establish reproducible withdrawal activity loss.
After complete anesthesia was achieved, a mid-sagittal section was made on the anterior abdominal wall, followed by an injection of 1000 IU heparin into the exposed abdominal vein, 10 s prior to harvesting the heart. The heart was excised and arrested in ice-cold Krebs–Henseleit (KH) buffer. The aorta was cannulated and the heart retrogradely perfused from a reservoir 90 cm above the heart. Special care was taken in order to maintain the perfusate’s upper level at 100 cm. The hearts were perfused with non-recirculating KH buffer containing 120 mM NaCl, 5.9 mM KCl, 1.2 mM MgSO4, 1.2 mM KH2PO4, 1.25 mM CaCl2, 25 mM NaHCO3, and 11 mM glucose at pH 7.4. The perfusate was equilibrated with 95% O2 and 5% CO2 and maintained at a temperature of 37°C. The isolated rabbit hearts were perfused for at least 30 min with KH buffer or until baseline functional parameters were established prior to the start of the experiment.
A Sony HDR-CX100 Full-HD (1920 × 1080, 30 fps) CCD camera was used to record the beating heart. Additionally, suitable illumination was adjusted to eliminate shadow and inappropriate reflections. Two continuous recordings, one minute each, were acquired from the anterior angle. The first recording was obtained at the initiation of the experiment, i.e. 20 min post stabilization of functional parameters. The second recording was obtained 4 min after the first (after complete flow cessation of the perfusate for 1.5 min and subsequent reinitiation of the perfusate for 2.5 min).
Data acquisition
The CCD camera was placed at an approximately 20 cm distance from the surface of the beating heart. In order to have a clear focus on the heart‘s surface, a white light emitting diode (LED) array was positioned in front of the heart to illuminate it. An appropriate background able to provide adequate contrast was placed (Figure 1). In most experiments, a black or green textile was chosen. This was placed behind the heart as background, in order to reduce backscatter light and facilitate the recognition and isolation of the heart‘s contour. The acquisition model also allowed rotation of the CCD camera around the heart in order to record the heart‘s functioning from several angles. Although a variety of oblique and lateral views was used, the anterior angle was concluded to be the most reproducible and sensitive one. Thus, it will be the only one to be reported here.
Figure 1: Video images of the heart at diastolic and systolic phases before and after image processing. (A) RGB image of the heart at systolic phase. (B) RGB image of the heart at diastolic phase. (C) Binary image of the heart at systolic phase after image processing. (D) Binary image of the heart at diastolic phase after image processing.
Data processing
Each frame of the recorded video file was converted into high quality (RGB bmp format) images. MATLAB (The Mathworks 2009a) software was developed, in order to process the acquired video images. The image processing was achieved using MATLAB functions on each individual frame, in order to isolate the beating heart from the contrasted background. Additional algorithmic methods were used to eliminate the noisy reflections produced by the water drops. The resultant RGB images were converted into binary (bmp format) images (Figure 1).
Several morphometric parameters were calculated to evaluate the heart’s function, in order to assess the ability of each parameter to reflect reliably and reproducibly a difference between the normal and hypoxic heart. Among several computations studied, we outline the most sensitive ones found to depict the heart’s contractility:
A. The percentile change of the projected surface of the heart at each frame (1/30 s), i.e. the percentile difference between a given time measurement and the minimum measurement observed on the same heart.
The minimum of the surface projection at each cardiac cycle corresponds to the most shrunk projected surface (Sminabs) of the heart which was invariably observed at the maximum systole. The maximum surface projection at each cardiac cycle corresponds to the end-diastole (Smaxabs). The minimum of the vertical length of the heart (Lminabs) which was invariably observed at the maximum systole. The maximum of the vertical length of the heart (Lmaxabs) corresponds to the end-diastole. Given the fact that the absolute metric measurements of the projected surface may vary not only for different heart sizes but also for the same heart, due to camera parameters (autofocus, magnification) we use percentile changes that are calculated with reference to the minimum values observed over given k frames. Relative values which indicate percentile changes of referred minimum absolute values, as follows. At end-diastole the percentile change of the projected surface becomes maximum.
For each of the k binary images we calculate  which corresponds to the projected surface of a given time-frame. Each cardiac cycle presents a Sminabs which corresponds to the minimum S during a cardiac beat. The minimum Sminabs of all k images (thus for all cardiac cycles) is calculated by
which corresponds to the projected surface of a given time-frame. Each cardiac cycle presents a Sminabs which corresponds to the minimum S during a cardiac beat. The minimum Sminabs of all k images (thus for all cardiac cycles) is calculated by 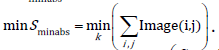 The percentile surface projection change is given by
The percentile surface projection change is given by 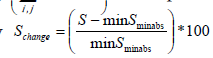 for each frame.
for each frame.
The minimum percentile surface projection change (Smin) for each cardiac cycle (corresponding to end-systole) is calculated by 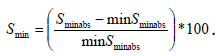 The maximum percentile surface change (Smax) for each cardiac circle (corresponding to end diastole) is calculated by
The maximum percentile surface change (Smax) for each cardiac circle (corresponding to end diastole) is calculated by 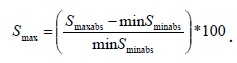
B. For each of the k binary images we calculate 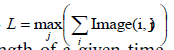 which corresponds to the maximum vertical length of a given timeframe. Each cardiac cycle presents Lminabs which corresponds to the minimum L during a cardiac beat. The minimum Lminabs of all k images thus for all cardiac cycles is calculated by
which corresponds to the maximum vertical length of a given timeframe. Each cardiac cycle presents Lminabs which corresponds to the minimum L during a cardiac beat. The minimum Lminabs of all k images thus for all cardiac cycles is calculated by 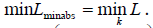 percentile vertical length change is given by
percentile vertical length change is given by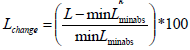 for each frame. The percentile change of the vertical length of the heart at each frame, i.e. the percentile difference between a given measurement and the minimum elongation observed, which was invariably observed at the maximum systole.
for each frame. The percentile change of the vertical length of the heart at each frame, i.e. the percentile difference between a given measurement and the minimum elongation observed, which was invariably observed at the maximum systole.
The minimum percentile vertical length change (Lmin) for each cardiac cycle (corresponding to end-systole) is calculated by 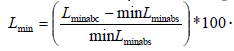 The maximum percentile vertical length change (Lmax) for each cardiac circle (corresponding to end diastole) is
The maximum percentile vertical length change (Lmax) for each cardiac circle (corresponding to end diastole) is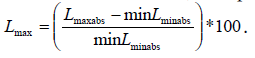
C. The ratio (max vertical length over max horizontal length) of the heart over time. For each of the k binary images the maximum vertical length, observed at end diastole, is given by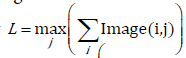 and the maximum horizontal length is given by
and the maximum horizontal length is given by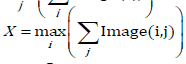 (Figure 1). We then can compute the ratio
(Figure 1). We then can compute the ratio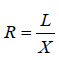 for each frame at a given time. The maximum ratio (Rmax) for each cardiac circle (corresponding to end-diastole) is ginen by
for each frame at a given time. The maximum ratio (Rmax) for each cardiac circle (corresponding to end-diastole) is ginen by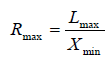 . The minimum ratio (Rmin) for each cardiac circle (corresponding to endsystole) is given by
. The minimum ratio (Rmin) for each cardiac circle (corresponding to endsystole) is given by 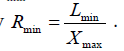
All these parameters were represented in draw graphics. Sample graphics of the normal and hypoxic heart are depicted in Figure 2 and Figure 3.
Figure 2: Diagrams showing the percentile change of the projection surface, the percentile change of the vertical length and the ratio for both normal and compromised heart over time. (A) Normal heart’s percentile change of the projected surface. (B) Compromised heart’s percentile change of the projected surface. (C) Normal heart’s percentile change of the vertical length. (D) Compromised heart’s percentile change of the vertical length. (E) Normal heart’s ratio. (F) Compromised heart’s ratio.
We evaluated 6 normal rabbit hearts (nH1-nH6) before and after they were subjected to 1.5 min of hypoxia (compromised hearts (cH1- cH6)), via cessation of the perfusate, as described above. The results are shown in Table 1 and Figure 4.
| nH1 | nH2 | nH3 | nH4 | nH5 | nH6 | cH1 | cH2 | cH3 | cH4 | cH5 | cH6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mean Smax | 7.26% | 7.86% | 6.62% | 7.94% | 6.84% | 7.63% | 3.27% | 2.17% | 4.20% | 3.72% | 2.48% | 3.83% |
| mean value of Smax | 7.36% | 3.28% | ||||||||||
| SD | 0.54% | 0.80% | ||||||||||
| mean Smin | 0.47% | 0.40% | 0.55% | 0.50% | 0.42% | 0.46% | 0.36% | 0.25% | 0.47% | 0.44% | 0.27% | 0.44% |
| mean value of Smin | 0.47% | 0.37% | ||||||||||
| SD | 0.05% | 0.10% | ||||||||||
| mean Lmax | 14.58% | 16.32% | 13.87% | 12.72% | 13.48% | 15.32% | 4.19% | 2.84% | 5.56% | 4.37% | 2.88% | 4.98% |
| mean value of Lmax | 14.38% | 4.14% | ||||||||||
| SD | 1.31% | 1.10% | ||||||||||
| mean Lmin | 0.49% | 0.64% | 0.53% | 0.38% | 0.42% | 0.56% | 0.32% | 0.21% | 0.44% | 0.37% | 0.24% | 0.41% |
| mean value of Lmin | 0.32% | 0.33% | ||||||||||
| SD | 0.04% | 0.09% | ||||||||||
| mean Rmax | 1.661 | 1.713 | 1.637 | 1.672 | 1.641 | 1.698 | 1.36 | 1.41 | 1.372 | 1.423 | 1.364 | 1.358 |
| mean value Rmax | 1.669 | 1.381 | ||||||||||
| SD | 0.02805 | 0.02809 | ||||||||||
| mean Rmin | 1.271 | 1.314 | 1.307 | 1.299 | 1.269 | 1.258 | 1.3 | 1.321 | 1.298 | 1.358 | 1.304 | 1.332 |
| mean value of Rmin | 1.286 | 1.319 | ||||||||||
| SD | 0.0232 | 0.02333 | ||||||||||
Table 1: Normal hearts' (nH1-nH6) and compromised hearts' (cH1-cH6) mean values and standard deviation (SD) of maximum values (mean value of Smax) of percentile surface projection (mean Smax); mean minimum values (mean value of Smin) and standard deviation (SD) of percentile surface projection (mean Smin); maximum values (mean value of Lmax) and standard deviation (SD) of percentile vertical length (mean Lmax); minimum values (mean value of Lmin) and standard deviation (SD) of percentile vertical length (mean Lmin); maximum values (mean value of Rmax) and standard deviation (SD) of ratio (mean Rmax) and minimum values (mean value of Rmin) and standard deviation (SD) of ratio (mean Rmin).
Figure 4: Normal and compromised hearts’ mean values comparison. (A) Comparison of normal and compromised hearts’ mean values (mean Smax) of maximum values of percentile surface projection (Smax). (B) Comparison of normal and compromised hearts’ mean values (mean Smin) of minimum values of percentile surface projection (Smin). (C) Comparison of normal and compromised hearts’ mean values of maximum values (mean Lmax) of percentile vertical length (Lmax). (D) Comparison of normal and compromised hearts’ mean values of minimum values (mean Lmin) of percentile vertical length (Lmin). (E) Comparison of normal and compromised hearts’ mean values of maximum values (mean Rmax) of ratios (Rmax). (F) Comparison of normal and compromised hearts’ mean values of minimum values (mean Rmin) of ratios (Rmin).
The image processing of the projected heart’s surface showed that the surface projection of the heart, which corresponded to its ability to shrink, was reduced in the heart compromised by hypoxia. Since the surface projection of each heart was different and dependent on the animal’s size, we eliminated this bias by using the relative percentile change of the projected surface that took into account the size and dimensions of each individual heart. The relative percentile change was expressed as a percentile fraction of the surface projection measurement at each frame divided by the minimum surface projection observed, corresponding to the end of systole.
The mean values of the percentile surface projection changes are outlined in (Table 1).
Mean Smax is the mean value of all the maximum values (Smax) of the percentile projection surface change in each heart. Mean value of Smax is the mean value of the mean Smax values for all six hearts. The mean Smax varied between 6.617-7.935% in normal hearts (nH1-nH6), whereas the respective values in the compromised hearts (cH1-cH6) subjected to hypoxia for 1.5 min ranged between 2.174–4.197%.
Mean Smin is the mean value of all the minimum values (Smin) of the percentile projection surface change in each heart. Mean value of Smin is the mean value of the mean Smin values for all six hearts. The mean Smin varied between 0.4032–0.5491% in normal hearts (nH1-nH6), whereas the respective values in the compromised hearts (cH1-cH6) subjected to hypoxia for 1.5 min ranged between 0.2475–0.4734%.
Mean Lmax is the mean value of all the maximum values (Lmax) of the percentile change of the vertical length in each heart. Mean value of Lmax is the mean value of the mean Lmax values for all six hearts. The mean Lmax varied between 12.72-16.32% in normal hearts (nH1-nH6), whereas the respective value in the hypoxic (compromised) hearts (cH1-cH6) ranged between 2.843–5.561%.
Mean Lmin is the mean value of all the minimum values (Lmin) of the percentile change of the vertical length in each heart. Mean value of Lmin is the mean value of the mean Lmin values for all six hearts. The mean Lmin varied between 0.378–0.6391% in normal hearts (nH1-nH6), whereas the respective values in the compromised hearts (cH1-cH6) subjected to hypoxia for 1.5 min ranged between 0.2056–0.4391%.
A representative sample displaying the Lmin, Lmax and intermediate values is shown in Figure 3.
Mean Rmax is the mean value of all the maximum ratio values (Rmax) in each heart. Mean value of Rmax is the mean value of the mean Rmax values for all six hearts. Mean Rmax observed on the normal hearts were distributed between 1.637–1.713, whereas in the hypoxic compromised heart the same values ranged between 1.358–1.423.
Mean Rmin is the mean value of all the minimum ratio values (Rmin) in each heart. Mean value of Rmin is the mean value of the mean Rmin values for all six hearts. Mean value of Rmin is the mean value of the mean Rmin values for all six hearts. Mean Rmin observed on the normal hearts were distributed between 1.258–1.314, whereas in the hypoxic compromised hearts the same values ranged between 1.298–1.358.
All these morphometric parameters showed that the ability of the heart to contract and shrink was less in the compromised by hypoxia rabbit heart. It also indicated that the heart’s ability to shrink reflected its contractility. Another interesting finding was that each of the normal hearts displayed more surface projection beat to beat variability compared to the hypoxic heart.
Mean Sdif is the mean value of the differences (Sdif) between the Smax and Smin for each heart. The mean Sdif(s) of the six (6) normal hearts are compared to the corresponding compromised hearts’ values. This comparison is shown in Figure 5A and is depicted in full detail in Table 2.
Figure 5: Normal and compromised hearts’ mean difference values comparison. (A) Comparison of normal and compromised heart’s mean values (mean Sdif) of difference values of percentile surface projection (Sdif). (B) Comparison of normal and compromised heart’s mean values of difference values (Mean Ldif) of percentile vertical length (Ldif). (C) Comparison of normal and compromised hearts’ mean values of difference values (Mean Rdif) of ratio (Rdif).
| nH1 | nH2 | nH3 | nH4 | nH5 | nH6 | cH1 | cH2 | cH3 | cH4 | cH5 | cH6 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mean Smax | 7.26% | 7.86% | 6.62% | 7.94% | 6.84% | 7.63% | 3.27% | 2.17% | 4.20% | 3.72% | 2.48% | 3.83% | |
| mean Smin | 0.47% | 0.40% | 0.55% | 0.50% | 0.42% | 0.46% | 0.36% | 0.25% | 0.47% | 0.44% | 0.27% | 0.44% | |
| Sdif= mean Smax - mean Smin | 6.79% | 7.46% | 6.07% | 7.44% | 6.42% | 7.17% | 2.91% | 1.93% | 3.72% | 3.29% | 2.22% | 3.39% | |
| Mean Sdif | 6.89% | 2.91% | |||||||||||
| SD | 0.57% | 0.70% | |||||||||||
| p-value | 0.0313 | ||||||||||||
| mean Lmax | 14.58% | 16.32% | 13.87% | 12.72% | 13.48% | 15.32% | 4.19% | 2.84% | 5.56% | 4.37% | 2.88% | 4.98% | |
| mean Lmin | 0.49% | 0.64% | 0.53% | 0.38% | 0.42% | 0.56% | 0.32% | 0.21% | 0.44% | 0.37% | 0.24% | 0.41% | |
| Ldif= mean Lmax - mean Lmin | 14.09% | 15.68% | 13.34% | 12.34% | 13.06% | 14.76% | 3.87% | 2.64% | 5.12% | 4.00% | 2.64% | 4.56% | |
| mean Ldif | 13.88% | 3.81% | |||||||||||
| SD | 1.22% | 1.76% | |||||||||||
| p-value | 0.0313 | ||||||||||||
| mean Rmax | 1.661 | 1.713 | 1.637 | 1.672 | 1.641 | 1.698 | 1.36 | 1.41 | 1.372 | 1.423 | 1.364 | 1.358 | |
| mean Rmin | 1.271 | 1.314 | 1.307 | 1.299 | 1.269 | 1.258 | 1.3 | 1.321 | 1.298 | 1.358 | 1.304 | 1.332 | |
| Rdif = mean Rmax-mean Rmin | 0.39 | 0.399 | 0.33 | 0.373 | 0.372 | 0.44 | 0.06 | 0.089 | 0.074 | 0.065 | 0.06 | 0.026 | |
| mean Rdif | 0.384 | 0.0623 | |||||||||||
| SD | 0.03627 | 0.02091 | |||||||||||
| p-value | 0.0313 | ||||||||||||
Table 2: a) Normal hearts' (nH1-nH6) and compromised hearts' (cH1-cH6) mean maximum values (mean Smax) of percentile surface projection (Smax); mean minimum values (mean Smin) of percentile surface projection (Smin); the difference between mean maximum values and mean minimum values of percentile surface projection (Sdif,); the mean value (mean Sdif) of the Sdif (s) of either set of hearts (normal and compromised heart sets); the standard deviation (SD) of the difference values of percentile surface projection and the p-value of all normal heart’s Sdif and all compromised heart’s Sdif.
b) Normal hearts' (nH1-nH6) and compromised hearts' (cH1-cH6) mean maximum values (mean Lmax) of percentile vertical length (Lmax); mean minimum values (mean Lmin) of percentile vertical length (Lmin); the difference between mean maximum values and mean minimum values of percentile vertical length (Ldif,); the mean value (mean Ldif) of the Ldif (s) of either set of hearts (normal and compromised heart sets); the standard deviation (SD) of the difference values of percentile vertical length and the p-value of all normal heart’s Ldif and all compromised heart’s Ldif.
c) Normal hearts' (nH1-nH6) and compromised hearts' (cH1-cH6) mean maximum values (mean Rmax) of ratio (Rmax); mean minimum values of ratios (mean Rmin) of ratio (Rmin); the difference between mean maximum values and mean minimum values of ratio (Rdif); the mean value (mean Rdif) of the Rdif (s) of either set of hearts (normal and compromised heart sets); the standard deviation (SD) of the difference values of ratio and the p-value of all normal heart’s Rdif and all compromised heart’s Rdif.
On the same lines, Mean Ldif is the mean value of the differences (Ldif) between the Lmax and Lmin for each heart. The Ldif(s) of the normal and compromised hearts are shown in Figure 5B and Table 2.
The mean Rdif is the mean value of the differences (Rdif) between the Rmax and Rmin for each heart. The Rdif(s) of the normal and compromised hearts are shown in Figure 5C and Table 2.
Using the Wilcoxon sign rank test, the p value was calculated for Sdif, Ldif and Rdif. All three p-values were found <0.05, thus proving that Sdif, Ldif and Rdif were satisfactory indices of the heart’s function.
The Wilcoxon sign rank test was chosen over the t test, so as not to risk the assumption that the data has a Gaussian distribution.
This study used a commercial CCD camera. A specialized Software was created using MATLAB to evaluate morphometric and dimensional changes of the isolated beating heart. It was concluded that the projected surface of the heart was able to reflect adequately and reproducibly even subtle changes in the rate and contractility. At first, the beating heart‘s projected surface and variations between systole and diastole were estimated. This appeared to be a sensitive indicator of the heart‘s contractile function. At second, the beating heart‘s elongation in the vertical axis was estimated. The hypoxic heart displayed a lower degree of elongation in comparison to the normal heart, which reflects changes in the diastolic relaxation, associated to hypoxia. A greater degree of relaxation was observed in the normal heart compared to the hypoxic one. At third, the beating heart‘s ability to shrink and increase its transverse diameter was estimated. The hypoxic heart displayed a smaller degree of dilation in the horizontal axis which was a reflection of the systolic shrinkage and by extension of the contractility. At fourth, as a measurement of the heart‘s ability to both relax and contract, the ratio of the vertical to the horizontal axis was estimated. This appeared to be an augmented, sensitive index of contractility, able to produce amplified peak values and therefore display in a more enhanced manner the differences between the normal and hypoxic heart. This becomes evident, if one considers that at full relaxation the heart‘s length was maximum, at the same time the transverse diameter was minimum, whereas at complete systole this ratio is reversed.
Both the black and green backgrounds were found to be able to provide satisfactory contrast. The view angle of the projected surface produced a variety of measurements which all appeared to be sufficiently sensitive and specific. However, the anterior projection of the heart‘s surface was clearly the most easily defined and reproduced.
Physiological assessment of the isolated beating heart is traditionally based on direct left ventricular pressure measurements. On the contrary, human heart physiological assessment is mainly based on anatomical changes, tissue and flow velocities via Echo, Magnetic Resonance Imaging (MRI) and fluoroscopic methods. The disparity in the methods used between the human and small animal hearts relies largely on the ability for invasiveness in the experimental methods. However, it also relies on our inability to measure precise dimensional changes on a small size beating heart, with a cost effective method.
Left Ventricular Developed Pressure (LVDP) is the most widely used measurement of the cardiac performance on the Langendorff’s isolated heart perfusion system. It was adopted early in the genesis of cardiac experimental physiology, as it was easy to use a water-filled balloon in one of the cardiac chambers and transfer this pressure through a hydraulic system to an appropriate recording system. The combination of this simple principle with the later developed advanced piezoelectric and fiber optic sensor technologies, as well as a variety or software tools, allowed continuous evaluation and recording of the LVDP and extraction of valuable calculated conclusions, such as the pressure volume loops.
Although the balloon measurement approach relies on the principle of Pascal law, stating the immediate pressure transmission in a liquid medium, we often neglect to take into account certain imperfections of the method, both operator and non-operator dependent, which add significant bias on the results:
a) The LVDP is the product of competition between a fixed size balloon and the cardiac chamber (i.e. commonly the Left Ventricle (LV)), as an overinflated balloon exerts certain diastolic load and may augment the LVDP in a nonmeasurable or predictable manner.
b) The water pressure of the water-filled balloon compromises the myocardial perfusion, especially as the heart becomes edematous.
c) The shape conformity of a spherical balloon in the pyramid shaped LV is impossible, especially concerning the interior and apical segments of the heart therefore an element of accurate contractility measurement is lost.
d) The balloon provides an averaged global measurement of systolic function, without any information on regional dynamics.
e) It is impossible to ascertain pressure volume relationships as left ventricular dimensions remain stable.
f) To overcome the above limitations, this study has established a simple and contactless method to assess the beating heart’s dimensional changes. These dimensional changes are LV volume independent, eliminate operator dependent bias and appear accurate in providing dimensional changes over the cardiac cycle. In addition, this method is simple, cost-effective, reproducible and can be used in both large and small animals. Although we have analysed the retrogradely perfused beating heart, the same method can be easily applied to the working heart model.
Certain considerations need to be addressed in establishing the reproducibility and accuracy of the method: The background conditions need to be carefully adjusted in order to obtain continuously a sufficiently contrasted cardiac shadow. The light conditions need to be modified, so as to be able to eliminate reflections that produce optical noise. An imaging algorithm able to extract accurately the pixel proportion reflecting the cardiac shape was established. Water drops may increase the optical noise of the reflections and need to be avoided, as they increase the imaging, processing and analysis time. Drops tend to accumulate at the apical segments of the beating heart and they are independent of the heart’s size. Although not presented here, the same method was used to assess the rat and the mouse heart. As expected, the drops’ volume appeared to be constant, depending at large on the surface tension forces of the solution. The drop-induced optical noise appeared to be higher in proportion with the smaller animal heart, and that increased the analysis time. In the beating rabbit heart, this problem was only limited due to size correlations between the drop size and the beating heart. In the small animal heart, as it will be depicted in subsequent reports, this problem was resolved by a simple method used by Oscar Langendorff himself [5] to measure the length and tension of the beating heart: A suture was threaded through the apex of the heart and a light weight was attached to the other end of it. The suture provided a path for the continuous flow of the perfusate, preventing the formation of big drops.
Although accurate temperature control wasn’t a particular aim of the current experiment, and therefore a water bath around the beating heart was not used, in two variations of the experiment, a continuous flow of warm solution and a low flow of warm air around the heart was used to keep the temperature perfectly controlled. However, although not presented, the temperature control didn’t appear to be a particular concern. In fact, it appeared that the selection of the appropriate energy level light-source and the appropriate distance for illumination were more critical factors in determining the beating heart’s temperature, which was frequently high, and therefore the distance had to be increased to cool down the heart.
In conclusion, the new method presented in this paper is contactless, unbiased, cost effective, simple and can be used to evaluate the cardiac function in an ex vivo working model. Further work is needed to ameliorate image processing algorithms in order to improve accuracy and obtain the results in real time.
We express our gratitude to Prof. George Kostopoulos and the Laboratory of Physiology at the University of Patras Medical School for providing us workspace and financial support. We thank Advanced Biomedical Instruments (Abi-med) for donating us the electronic equipment to perform LV pressure monitoring and LV temperature measurements. We also thank Emil Valchinov for his valuable technical support on hardware and software matters.