Journal of Physical Chemistry & Biophysics
Open Access

A Possible Explanation for the Twin Paradox and Action at a Distance: The Relative Independence of Space and the Absoluteness of Simultaneity

Sheng Qin^{* *}Correspondence: Sheng Qin, Department of Economics, Southwestern University of Finance and Economics, Chengdu, China, Email:

Author info »

Introduction

Einstein, et al. [1], once said that solving the twin paradox is beyond the scope of special relativity. Although particle decay in cosmic rays can prove the clock slowing effect to a certain extent [2,3], the twin paradox still puzzles many physicists. For example, Guangda, et al. [4], and others believe that it is impossible to solve the twin paradox within the scope of special relativity. And Shangwu, [5], once mentioned a method when analyzing this problem that is to use the time transformation of different reference frames to explain the premise of which is still the asymmetry of the movement process. For example Muller, [6], first solved this problem in 1972, and its premise is still based on an asymmetric reference frame. However, this paper hopes to set the premise of the twin paradox more strictly, and discuss it on the basis of complete symmetry. Based on this, we will infer a different conclusion from the past, that is, simultaneity in different reference frames can be established. In addition, we also deduce another interesting conclusion, which is that the spaces seem to be relatively independent. Although we have many experiments in the past to confirm the unity of the inertial frame space [7,8], the method proposed by the author in this paper is unique and is based on a detection method between different inertial frames.

The author found that these two conclusions can be used to explain many phenomena, such as: Twin paradox, quantum entanglement at a distance, cosmic inflation and other phenomena. The authors believe that this tentative explanation is possible.

Literature Review

Another tentative explanation of simultaneity and space in special relativity

A new tentative interpretation of “simultaneity” in Einstein's special theory of relativity: As shown in Figure 1, this is the description of the concept of simultaneity in the classic Einstein thought experiment [9]. The train moves in the direction of the X-axis at a speed V, and a beam of light is emitted from both ends of the platform at the same time. To an observer at the midpoint on the platform, the two beams appear to arrive at the same time; however, to a person on the train, the light in front of the movement will arrive before the light behind. Therefore, Einstein considered simultaneity to be relative [9].

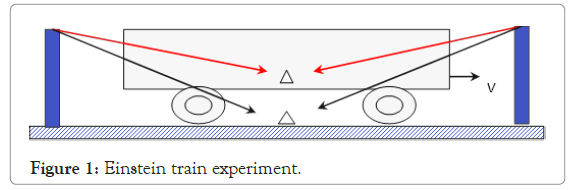
Figure 1: Einstein train experiment.

However, what this article should point out is: If the speed V of the train relative to the ground is known, then the people on the train can actually calculate and correct the “phenomenon” that the lights on the platform arrive successively. A person can correct the so-called “simultaneity” confusion by eliminating the time difference between the arrival of the two beams of light before and after. After the correction, the people on the train will also realize that the two beams of light shine at the same time.

If the person on the train sees that the time of arrival at the speed of light in front is t₀, the distance from the light-emitting point of the front platform is L₀ when it arrives; the time of arrival at the speed of light behind is t₁, and the distance from the light-emitting point of the rear platform when it arrives is L₁, the train and the ground the relative motion speed is v.

Then, after calculating the moment when the platform ahead is illuminated is: t₀− Δt , where

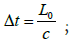
The moment when the rear platform glows is: t₁− Δt′ , where

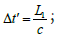
After the correction, the people on the train actually looked like the lights on both ends of the platform happened at the same time, that is: t₀ − Δt = t₁− Δt′ .

A new tentative explanation for the cognition of space in the special theory of relativity: As shown in Figure 2, an object moves at a constant speed relative to the ground along the X-axis direction at a speed V, and a beam of light is emitted from point A to point B inside the moving object. It is assumed that the observation system of the moving object is the S' system, and the ground coordinate observation system is the S system.

Figure 2: Light speed trajectories seen in different reference frames.

In the eyes of the observer of the S' system, the beam of light is moving in a straight line from A to B, and the moving distance is the straight-line distance between AB and the speed is the speed of light C; but in the view of the S system, the beam of light is actually moving obliquely (right side of Figure 2).

According to the principle of the constant speed of light, the observer of the S system requires the time of the S' system to slow down, otherwise there will be a dilemma of superluminal speed. What this article wants to amend is: In fact, the S system and S' system spaces are relatively independent. For the observer of the S system, unless it enters the “space” of the moving object S' system, this beam of light is “invisible” to the system S.

For the S system observer, this beam of light is “invisible” to the S system unless it enters the inertial frame of the moving object S' system. An observer of the S system wants to see the propagation process of a beam of light on the S' system, the premise is that the observer of the S system must first observe the beam of light, and the premise of the observation is: Either this beam of light is observed in the S system, so the beam of light and the matter of the inertial frame of the observer has acted; or the observer of the S system enters the S' system to observe.

Therefore, the so-called “speed of light is constant”, the premise is that the speed of light is measured in an inertial frame. Any measurement of the speed of light requires at least two points in the inertial frame as references. Therefore, it is not permissible to say: “In the same time, the beam of light travels longer than the S' system in the view of the S system” without making a measurement.

The twin paradox explained by the special theory of relativity: We know that the current theoretical explanation for the twin paradox mainly focuses on the asymmetry between the two reference frames. Many articles will explain that the process of “rocket acceleration” causes this time difference [10].

However, we can redesign the twin paradox experiment to better illustrate that the “accelerating process” is not the cause of the slowdown: Suppose that A and B are exactly the same rigid body, and two clocks with the same structure are placed on them and the initial positions of the clock hands are the same. After the two sides are accelerated with the same force (which can be accelerated by the spring connecting A and B), the relative motion speed of A and B becomes V. The two parties agree that at a certain “time t” of the clock, A and B will decelerate and return in a certain set of the same program, and finally decelerate in the same way to reach a relatively stationary state.

In such an experiment, all the motion processes of objects A and B are completely symmetrical.

According to special relativity, when A and B return to their final state of relative rest, A will see the clock on B slow down; B will also see the clock on A slow down. If a ground observer is the third observer relative to A and B, it will be found that the whole motion process of A and B is completely symmetrical, including the position of the clock hands. In the whole process, we cannot find that A or B have any unique advantages in the process of motion relative to each other, so it is difficult for us to explain the dilemma of “clock slowing down” in special relativity. Therefore, the dilemma of twin paradox is real and cannot be eliminated by the difference of acceleration process.

Defining time, space and simultaneity in inertial frame

Inertial system: We assume that the physical laws of any inertial system are the same, which is actually equivalent to assuming that the physical laws of the interaction between identical substances in any inertial system are the same.

For example, we assume that electrons, protons and neutrons are identical particles, and the physical relationship between the nucleus, the interaction between the nucleus and the extranuclear electrons, mass and energy is the same in any inertial system.

In any inertial system, we can use a certain fixed-energy photon as a basis to define a unified standard of physical units such as energy, mass, length, and time. For example, we can use a certain known hydrogen atom energy level corresponding to a photon of frequency ω to uniformly define 1 second in any inertial frame as the time corresponding to the photon of this energy level oscillating ω times; at the same time, we can use the wavelength of the photon defines the unit of length; the energy of the photon defines the unit of mass, and so on. We first think that, in all inertial systems, the physical units such as time, space, length, energy, etc., which are uniformly defined in this way, are consistent, and the physical laws derived from such uniformly defined units are consistent.

First of all, we believe that in all inertial systems, the physical units of time, space, length and energy defined in this way are consistent, and the physical laws derived from the units defined in this way are consistent. For the non-inertial system, if we can calculate the influence of non-inertial factors (such as gravitational field, electromagnetic field, acceleration, etc.) on the mass, energy and length of these basic identical particles, then we can also consistently define the basic physical quantities such as time, length and mass in the non-inertial system.

Hidden behind the assumption that the laws of physics are the same in all inertial frames, we will find that there is a more profound prerequisite: The relative independence of space.

That is to say, the space of the inertial system must be relatively independent. If the space of the inertial system is not independent and is affected by the relative motion state with other inertial systems (such as relative motion speed, relative distance, etc.) then these variables will undoubtedly directly affect the relationship between all substances in the inertial system. Unless this action is completely proportional and linear to the physical relationship between all substances in the inertial frame, it will be difficult for us to obtain the property of “the physical laws of all inertial frames are consistent”.

Defining time and length: According to the previous definition, we can define the time and length in different inertial frames uniformly.

1. The unified definition of time and length in different inertial frames is based on the frequency and wavelength of some identical photons.

2. Then, we can infer that the corresponding lengths of two rigid rulers with the same structure in two different inertial systems should be the same (the results measured in different inertial systems with the lengths defined above should be the same), otherwise, different physical laws are needed to explain the differences, which will violate our assumption of inertial systems.

3. In any non-inertial system (acceleration field or gravitational field), after fully considering the influence of acceleration or gravitation, we define the time and length on this basis, and the same physical quantities such as mass, length and time should be the same.

Simultaneity: The simultaneous occurrence of two events means that in two reference frames S and S', respectively, at some instant t and t', a beam of light is emitted towards their midpoint, they arrive at the midpoint at the same time after taking into account the influence of the symmetry or asymmetry of space. Then we say that the t time in the S system and the t' time in the S' system occur at the same time.

The proof of the absoluteness of simultaneity and the relative independence of spaces

For two reference frames kept relatively stationary: We assume that there are two relatively stationary reference frames S and S' (e.g., two relatively stationary inertial frames, two relatively stationary objects in a gravitational field), as shown in Figure 3.

Figure 3: Light beams reflected back and forth in a still system.

Send a beam of light from point A in the S frame to point B in the S' frame, and let the beam bounce back and forth. (Note that we do not need to assume that the speed of light c is the same back and forth, nor do we need to assume that the speed of light in the S system and the S' system is the same, just need to ensure that the back and forth reflected photons return to the initial state with the same frequency, because the path is repeated).

Assume that the “local” time of the S or S' system corresponding to the “moment” of each photon being reflected is: 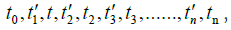as shown in Figure 3.

We assume: t′ = f (t) is the time transformation function between S and S' series.

Conclusion 1: We first prove that t′ = f (t ) it's linear.

Proof: Suppose that in the view of the S system, it takes time Δt₁ to travel from A to B at the speed of light, and it takes time Δt₂ to return from B to A. The corresponding in S' it appears that the time required to go from A to B and from B to A is respectively Δt'₁ and Δt'₂, then there is the following relationship:

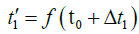
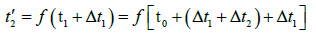
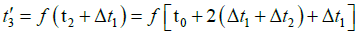
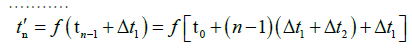
Due to the S' it seems that 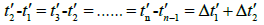Therefore, the left side of the equation is linear, and the variable relationship on the right side of the equation is also linear, and the time interval of the two coordinate systems 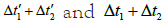is a linear relation, so that t ′ =f(t) it's linear. Prove it. Therefore, we can further assume that the linear relationship of the time function between the S system and the S' system is: t′=kt+b , in fact, if it is a real physical experiment, we can immediately obtain the coefficients b and k through the experimental data.

Conclusion 2: Prove K=1.

Prove: First, according to the assumption of inertial frame, the mass-energy equation in any reference frame E = mc² and Planck formula: E = hω (ω is the photon frequency), and it can be verified that identical substances have the same mass (such as electrons, protons, neutrons, etc.).

We assume that the times of the S and S' system have been uniformly defined in the manner described above, due to t ′= kt+b , so according to our previous definition of time, if K<1, according to the definition of simultaneity, means that 1 second has passed in the S system, and S' no more than 1 second has elapsed. It also means that photons of the same energy vibrate in the “1 second” time in the S system ω times, but at the same time S' it only vibrated in the system kω times.

However, in the above thought experiment, the time corresponding to the propagation process of the photon in the view of the S system and the S' system is respectively Δt₁ and Δt'₁, Δt'₂ and Δt'₂, the corresponding photon propagation path A→ B and B→ A it's exactly the same. Then it means that no matter the photon is in the S system or the S' system, the number of vibrations n of the photon in the propagation process of A→ B and B→ A is the same.

Then it means that no matter from the point of view of the S system or the S' system, Δt₁ and Δt'₁, Δt'₂ and Δt'₂ arecorresponding to the photons of the same energy vibrating the same number of times n, so according to our previous definition of time, we will get the following conclusion: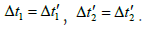

Thus, K=1. Prove it.

(Note: The above conclusion is not affected by whether the photon is in the gravitational field or the acceleration field, and whether it produces gravitational redshift. Because the number of times a photon oscillates during its propagation does not change whether it has a gravitational redshift or not).

Conclusion 3: In any relatively stationary frame of reference, we only need to properly adjust the positions of the hands of two identically constructed clocks to obtain a series of simultaneous clocks with exactly the same hands everywhere.

This is not only suitable for the inertial frame, but also for the two relatively static reference frames in the gravitational space, and for the acceleration frame in the relatively static state.

Proof for two reference frames in relative motion

Complete symmetry: After two rigid bodies A and B with the same structure obtain the same acceleration process (for example, a spring is used to connect the two ends of A and B to obtain acceleration), the relative motion speed of A and B becomes V, and the motion direction is the X-axis direction (the X-axis direction of A is the same as that of B).

According to symmetry, we should not think that either A or B has a relative advantage, for example, that A's time is faster than B's time, or that A's length shrinks in the direction of motion relative to B.

From our conclusions in the static system, we can obviously place a series of equidistant clocks on both A and B along the direction of their motion with the same positions of the clock hands. From the perspective of the A system, the positions of the clock hands on the A system are completely synchronized and strictly simultaneous; from the B system, the positions of the clock hands placed on the B system are also completely synchronized and strictly simultaneous, as shown in Figure 4 (assuming that A moves to the left and B moves to the right after acceleration).

Figure 4: Symmetrically accelerated rigid body and clock.

It is assumed that the coordinate positions of these clocks in their respective coordinate systems are:

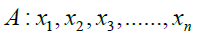
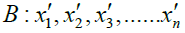
Their intervals are equal in their respective reference systems, and the intervals of these clocks are equal when comparing system A and system B in the static state, that is:

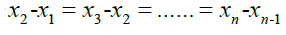
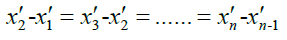
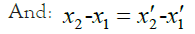
We assume that after A and B are accelerated, the coordinate origins of A and B systems coincide at time t₀, and x₁ and x'₁are exactly at the positions of A and B systems where x=0. At this time, the positions of all clock hands on A and B are time t₀.

Assuming that the coordinates of x'₂ and x₁ coincide exactly after Δt (at this times x'₃and x₂ coincidence,……, x'_k and xk- 1coincidence) in the view of the A system, the distance A runs relative to B within the time Δt is Δt.v . Since the “coincidence” is a fact, the event will only happen once at a certain time, either from the A system or to the B system point of view. Then we can obviously conclude that at some time in the A-system will 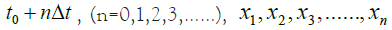coincide with 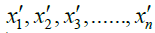they are overlapped with each other in turn (it is necessary to move the corresponding position sequence).

We assume that the time and length functions between the A and B systems are:

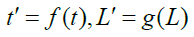
Then by symmetry one has:

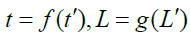
Therefore, every time the clocks of A system and B system coincide, we can see that the positions of the clock hands on the two coordinate systems are the same by comparing the clocks on A system and B system.

At the same time, if the coordinate points corresponding to two clocks are at a certain time t₀ +n Δt they do not coincide, the relative velocity of motion will not be equal to V.

For example, if t₀ moment x₁ and x'₁ coincidence, and t₀ moment x₂ and x'₂ do not coincide, then when passing through Δt time, according to the assumption of uniform motion in the t₀ + Δt the moment we will see x₁and x'₂ coincidence. But because t₀ moment x₂ and x'₂ do not coincide, then calculate at this time x'₂ at Δt the velocity of motion in time will get not V.

Therefore, we have the following important conclusions.

Conclusion 4: The relative length of A and B in the direction of motion is practically unchanged.

Conclusion 5: Since the lengths of inertial frames A and B correspond to the number of photon vibrations and the propagation distance of a certain frequency, it can be inferred that the clock trends of the two reference frames A and B are completely synchronous and strictly simultaneous.

For two non-symmetrical bodies C and D with relative velocity V: We can construct two identical rigid bodies, A and B, that are initially at rest relative to each other and have the same velocity and opposite directions relative to C and D, respectively (for example, V/2 relative to C and -V/2 relative to D), as shown in Figure 5.

Figure 5: Objects in asymmetric relative motion.

Then make A and B perform symmetrical acceleration motions in two directions, respectively. After acceleration, A remains stationary relative to C, and B remains stationary relative to D.

At this time, because A and C are relatively static, according to our previous conclusion in the static system, the clock hands between them will be completely synchronized and strictly simultaneous after adjustment. The same is true for B and D. According to the conclusion of the above thought experiment in the moving frame, both length and time between A and B are symmetrical and equal. Then it means that the clocks between C and D are also perfectly synchronized. If C and D are rigid bodies in an inertial frame, their lengths in the direction of motion will also be exactly the same.

Conclusion 6: Whether it is a static system or a dynamic system, the simultaneity in the inertial system is strictly established, and there is no effect of relativistic time slowing down; the lengths are also absolutely equal, and there is no effect of length contraction in the direction of motion. Even in the non-inertial system, these conclusions are still valid when we fully consider the influence of non-inertial factors.

Interpretation of relative independence of space and design of experimental test

Let's take the thought experiment of two identical rigid bodies, A and B, moving at a relative velocity of V. We have previously proved the equality of length and time. Then we assume t₀ moment x₁ and x'₁ at exactly the same position (X axis coordinates coincide), in the t₀ moments from A and B, respectively x₁ and x'₁ the coordinate positions emit a beam of light to the front at the same time, Δt after that (the time of the two coordinate systems is consistent), the beam of the A system arrives xp, the beam arrival of the B system x'p, as shown in Figure 6.

Figure 6: Experimental test of spatial relative independence.

t ₀+ Δt moment, x'p and xp at a distance of Δt.v ,that is to say, there is actually what we call “superluminal” phenomenon. Suppose we place a mirror at x'p to reflect the beam from the B reference frame to a point in the A reference frame immediately adjacent to x'p (ignoring the distance between the two reference frames), then we can find that when the light of the A system reaches xp, the light of the B system will reach 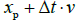at the same time after being reflected by the mirror, and the two beams of light will arrive at the time t₀ + Δt at the same time. The reason is not because of the “superluminal” phenomenon, but because of the relative spatial independence of A and B. The above thought laboratory can be tested by experiments. We can indeed emit the same beam of light to the B reference system through the relative independence of space, then reflect it forward through the mirror of the B reference system, and finally reflect it back to the A reference system through the mirror after reaching a certain point.

As long as the relative velocity of A and B is large enough, we can get a very significant “superluminal” effect.

(Note: Up to now, the author has not found any scientists who have done similar experiments). Our previous experiments to measure the speed of light were based on the same inertial frame.

Applications of the absoluteness of simultaneity and the relative independence of space: Explanation of quantum entanglement, supergiant interaction, cosmic inflation, newton's bucket experiment and Mach’s principle, measurement problem

Quantum entangled state problem and action at a distance: It is precisely because of the relative independence of space that two quanta are allowed to be in an independent entangled state.

Measurement means the destruction of the independent space of the entangled state, and also means the unification of the space where the entangled particles are located and the observation space where the measurement is located. Before the measurement, we can think that the entangled particles are in a relatively independent space. If the space does not have relative independence, it is impossible for us to separate two entangled particles without affecting the measured entangled particles.

As for the action at a distance of entangled particles, in fact, it will be explained naturally after we strictly prove the “absoluteness of simultaneity”. The “absoluteness of simultaneity” guarantees the instantaneous conservation of energy, momentum and angular momentum between two particles.

Conversely, if there is no “absolute simultaneity” as a guarantee, the relative independence of space will not be guaranteed. Because the conservation of energy and momentum between substances caused by the relative independence of space can only be guaranteed by absolute simultaneity.

The problem of particle orbits in atoms: At present, we use the uncertainty principle to answer the question of particles at the microscopic level. The premise of the assumption is that we have always believed that the space-time of microscopic particles is unified with the space-time of our observers. Only in a unified space-time can we uniformly specify the position, velocity and other information of particles.

However, if particles are relatively independent in space in the microscopic field, we will not be able to predict their state in independent space before observation, including speed, position and other information. Before observation, we cannot define the position, velocity and other information of a particle in another independent space unless we measure it.

A thought experiment on the expansion of the universe: We assume that there are object 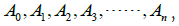, objects are moving along the X axis, and there is a lens on each object. Among A₁ relative A₀ has a velocity V, A₂ relative A₁ has a velocity V, Ak relative Ak-1 the velocity of is V, and so on, the velocity of the latter object relative to the former object is V, as shown in Figure 7.

Figure 7: Cosmic inflation thought experiment.

(Note: The velocity V marked in the figure refers to the relative velocity of the previous object, not to the observer.)

We assume that nv > c , with c the speed of light. Then we will get the following conclusion: A₀ and An the space between them will expand faster than the speed of light.

If a beam of light starts from A₀ and passes through the lenses on A₁, A₂ …… until there is a mirror on An, and then reflects the beam back in the same way.

For the sake of simplicity, let's assume that there are only 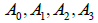these four bodies, they are moving at C/2 relative to the previous body, that is A₁ as opposed to A₀ moving at C/2, A₂ as opposed to A₁ moving at C/2, A₃ as opposed to A₂ moving at C/2, where C is the speed of light.

We assume that a beam of light is emitted from A₀ to A₁ at time t₀, and the distances between A₀ and A₁, A₂ and A₁, A₃ and A₂ are all L₁ at time t₀. This beam of light from A₀ to A₁ the time required for propagation is 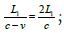the time at which the speed of light reaches A₁ is 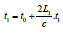moment A₁ , A₂ the distance is 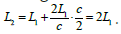The time required for the beam to go from A₁ to A₂ at time t₁ is 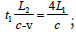Therefore, the time when the beam reaches A₂ is 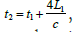and the distance between A₂ and A₃ 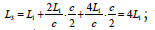is the time required for the beam to start from A₂ to A₃ at time t₂ is 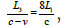and the time when the beam reaches A₃ is 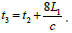When the beam reaches A₃, we assume that the distance between A₃ and A₂ at t3 is 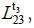the distance between A₂ and A₁ is 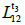and the distance between A₁ and A₀ is 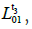then we have:

At this time A₀ to A₃ the actual distance of is: 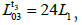compared to t₀ moment A₀ to A₃ the distance has increased 21L₁; and the speed of light from A₀ to A₃ the time has only passed: 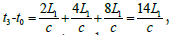therefore A₀ and A₃ the rate of space expansion between is:

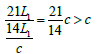
Obviously A₀ and A₃ the space between them expands faster than the speed of light C.

At the same time, the light beam can still return the same way, passing through 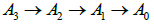respectively, and finally back to A₀, the light beam will not be unable to reach A₀ due to the superluminal expansion of the space between A₀ and A₃, because the space is relatively independent.

Corollary: The superluminal expansion of the universe does not mean that photons at both ends will never reach each other, but will reach each other through relatively independent spaces.

However, according to the velocity transformation formula of special relativity, we know that A₀ and A₃ their relative speed does not exceed the speed of light, so the distance between them does not increase faster than the speed of light. The reason for this is that there is no distinction between the relative independence of space in special relativity, which confuses two relatively independent spaces into a common space.

Explanation of Newton's bucket experiment and Mach's principle: We know that Newton understood absolute space with the bucket experiment; Mach explained the principle of relativity by saying that the water in the bucket moves relative to the whole universe [11].

Then, we consider the following thought experiment: Objects A, B and C, D have a rest mass of 2m respectively, and initially A, B, C, D and S remain at rest. Then, by consuming its own mass, it is converted into relative velocity, and the relative velocity of S is V (moving along the X axis of the S system). A, B, C and D respectively consume the energy corresponding to their own mass of m, as shown in Figure 7.

At this time, according to the conservation of momentum and energy, the kinetic masses of A, B, C and D are equal and equal in the S system:

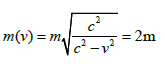
Where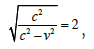 therefore, in the system, the energy momentum of A, B, C and D are conserved before and after acceleration.

According to the special relativistic velocity transformation formula [9], In the observation system of A, the velocities v_B and v_D of B and D are:

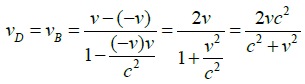
At this time, from the point of view of the A system, the dynamic masses m(vB) and m(vD) of B and D are:

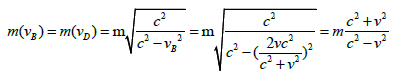
Then the total mass (corresponding to the total energy) of A and B seen from the perspective of the A system is:

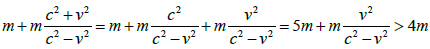
That is to say, if calculated according to the relativistic transformation formula, the total mass and energy of A and B increase after acceleration. However, according to the law of conservation of energy, this is impossible.

And if A and D collide, the static mass after the collision will be 4m, not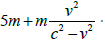

Explanation for this: In fact, the acceleration process of objects A and B is meaningful. When we talk about the relative velocity of A and B, it is not entirely related to the relative motion of objects A and B, but to the process of acceleration and the relative space S system of acceleration.

The so-called relative acceleration space is actually a “relatively independent” space composed of accelerated objects A, B and S, which is the inertial system space before acceleration.

Therefore, as Mach's principle points out, the relative “space” of water movement in the bucket is determined by the total space composed of our cosmic matter, and the conservation of energy and momentum is guaranteed by “absolute simultaneity”.

Conclusion 7: Space is determined and defined by matter, and the conservation of energy and momentum in our universe is guaranteed by the “absoluteness of simultaneity”.

If we analyze the above thought experiment more deeply, how do A and D determine their respective energies before the collision?

The answer is: Gravitational space.

If we assume that A emits a photon γ to D, then when D receives a photon γ, in addition to a Doppler blue shift effect, a gravitational red shift or gravitational blue shift due to the gravitational forces of A and D will also be observed shift effect. And the gravitational effect is based on the relative determinate energy of A and D, that is to say, before A and D collide, its own mass and energy have been determined. If we rely solely on the relative motion between objects A and D, we cannot determine their respective energies before the collision. Therefore, we will draw the following important conclusions.

Conclusion: Gravitational space is the only coordinate background space to determine the conservation of energy and momentum in our universe, and it requires strict simultaneity.

In other words, our universe has a coordinated background coordinate space to strictly determine the relative energy and momentum between cosmic matter.

Because if gravity travels at the speed of light, or gravitons travel at the speed of light, then a photon moving at the speed of light will not be affected by the gravitational redshift because it is stationary relative to the gravitational field or gravitons. Moreover, if strict simultaneity is not satisfied, the gravitational field will not be able to satisfy the instantaneous action on distant objects.

The relative independence of gravitational field space: By improving the thought experiment in Figure 8, we will gain further insight into the relative independence of space, as shown in Figure 9.

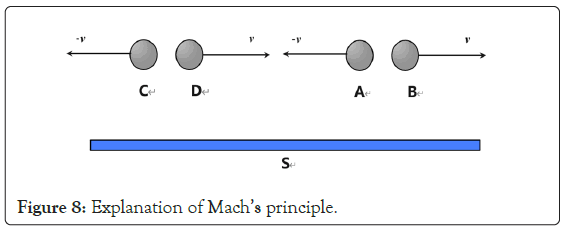
Figure 8: Explanation of Mach’s principle.

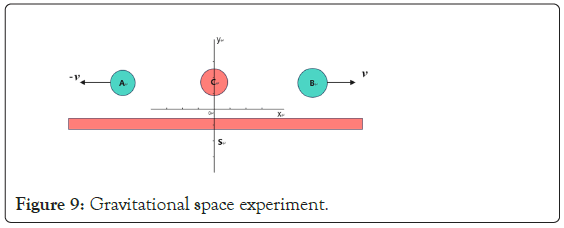
Figure 9: Gravitational space experiment.

The static masses of objects A, B, and C are m_A, m_B and m_C, respectively, of which object C has always remained in a relatively stationary state with the S system, while objects A and B are relative to the coordinate origin of the S system at velocities -v and v at time t₀, A and B moves in the X-axis direction of S system.

Then, no matter from the point of view of the S series, or from the perspective of the A series or the B series, the distances between them and C are the same, which are vt respectively (note that t here refers to the S series or the A series or the local time of B series).

In the special theory of relativity, the discussion of the relative distance L between two objects in relative motion is lacking [9], because the effects of clock delay and length contraction in the special theory of relativity are based on the observation of objects in the inertial frame of relative motion , and are relativistic; that is to say, these effects are only valid for inertial system objects in the special theory of relativity. There is no detailed discussion on how the relative distance between two objects in relative motion will be affected by clock delay and length contraction effects.

And according to special relativity's relativistic view of velocity, this will become even more vague and unclear. This article will demonstrate here in another way.

No matter from the point of view of the S series, the A series or the B series, the vt will be the same, and there will be no difference caused by the relativistic effect.

First, we need a reasonable assumption.

Assumption: For any event X, there is only one corresponding result in the frame of reference in which it occurs. For example, the time t when X occurs, the energy E, momentum P, object frequency and other physical phenomena corresponding to X are all determined.

We know that such an assumption is reasonable, otherwise our entire world would be thrown into a causal logic mess.

Then, if we assume that a photon γ is emitted from point C to A at time t₁ of the S system, and when the photon reaches A, it is reflected back to point C. If we ignore other objects and only consider the three objects A, B, and C, then the photon γ will be affected by the gravitational force of these three objects, and the distance of the photon γ under the gravitational action must be vt1gravitational influence of initial distance calculation.

Therefore, we can conclude that since the relative motion speed v between A and C is determined, then since the common distance L between them is consistent, the “simultaneity” will be absolute for them, otherwise we will not be able to conclude that the gravitational influence on photons is consistent from the point of view of both the C system and the A system, which once again proves our conclusion about simultaneity. (Here we ignore the proof that the relationship between gravitational action and distance is a monotonic function).

Conversely, if we assume that the photon γ1 starts from A to B at the same time when the photon γ reaches A, the photon γ first passes through a lens on the key point C on the way and then continues to emit to B, while γ1 will be directly emitted to B. At this point, we can easily draw the conclusion: From the perspective of A, whether it is a photon γ1 or a photon γ, the time it takes for them to reach B is the same, and the gravitational effects of A, B, and C during the period are also the same.

Since when the photon γ reaches A, the distances of AC and BC are both: 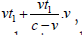then obviously, the gravitational effect of the photon γ1 during the propagation from A to B is affected by the impact will be calculated as the total initial distance between AB: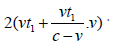

However, according to the speed transformation formula of special relativity, we know that the relative motion speed between AB at this time is:

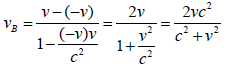
Therefore, according to the transformation formula of special relativity, when the photon γ reaches A, the distance between AB in the view of A is:

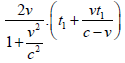
And apparently there are:

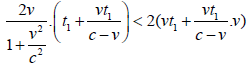
Therefore, this is contradictory. The starting distance of the actual gravitational action of photon γ₁ is 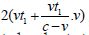which will not be changed by the speed change of special relativity. The only explanation is that the space is actually relatively independent. Even space is discontinuous in a sense.

The relative velocity between objects A and B is not the only factor that limits the size of the distance between A and B. We also need to consider the impact of other objects C on space. Therefore, we can also draw the following conclusions.

Conclusion: The continuity of space is not a rule that the universe must obey. The basic rule of the universe is the conservation of momentum and the conservation of energy. Therefore, when we observe the motion of microscopic objects, we will find that the positions of particles are random and do not actually follow the rules required by the continuity of space.

Discussion

Interpretation of measurements

We know that if we measure the spin direction of a particle, once we measure it and assume that the spin direction of the particle is upward, then if we repeat the measurement again, the spin direction will remain unchanged.

In fact, the measurement is a unified process of the independent space of the particle and the space of our measuring instrument. Before the measurement, the particle is in a relatively independent space, and its spin direction relative to the measuring instrument is not yet determined. After the measurement, the particles are no longer in a relatively independent state, but in a unified space with the measuring instrument. At this time, because of the conservation of the unified space, its spin direction will not change randomly. Of course, with the passage of time, microscopic particles always tend to be in a relatively independent spatial state (or entangled state), as long as the whole of microscopic particles maintains a global conserved state.

Conclusion

Based on the assumption that “all inertial frame physical laws are consistent”, this paper rigorously deduces the clock effect in both static and dynamic states, and demonstrates the absolute simultaneity of various reference frames and the relative independence of space. Two interesting conclusions, proving the possibility conclusion that “space is defined by matter”. It also explains the impossibility of the twin paradox under the premise of complete symmetry.

Based on this, this paper proposes an experimental test method for the independence of space; and based on the conclusion of this paper on simultaneity and relative independence of space: Tentatively explain the ultra-distance effect of quantum entanglement, the orbit of particles, the universe Inflation phenomenon, Mach principle, interpretation of measurement problems and other important physics problems. This paper proposes that the absoluteness of simultaneity is a necessary guarantee and a prerequisite for the conservation of energy and momentum in the relative independence of space, and is indispensable. At the same time, this paper attempts to strictly prove that Einstein's definition of simultaneity and spatial absoluteness in special relativity may be problematic.

References

1. Einstein A, Naturwiss E. On Einstein's resolution of the twin clock paradox. Curr Sci. 2015;89(12).
2. Rossi B, Hall DB. Variation of the rate of decay of mesotrons with momentum. Phys Rev. 1941;59(3):223.

   [Crossref] [Google Scholar]

3. Greenberg AJ, Ayres DS, Cormack AM, Kenney RW, Caldwell DO, Elings VB, et al. Charged-pion lifetime and a limit on a fundamental length. Phys Rev Lett. 1969;23(21):1267.

   [Crossref] [Google Scholar]

4. Guangda M, Runhua W. Impossibility of solving twin paradox within special relativity. Univ Phys. 1997;16(4).
5. Shangwu Q. The key to solving the clock paradox in special relativity. Nat Magazine. 1987;12(4).
6. Muller RA. The twin paradox in special relativity. Am J Phys 1972;40(7):966-969.

   [Crossref] [Google Scholar]

7. Silvertooth EW. Isotropy of C. J Opt Soc Am. 1972;62(11):1330-1331.

   [Crossref] [Google Scholar]

8. Trimmer WS, Baierlein RF, Faller JE, Hill HA. Experimental search for anisotropy in the speed of light. Phys Rev D. 1973;8(10):3321.

   [Crossref] [Google Scholar]

9. Einstein A. Translated by Yang Zi. Relativity. Beijing: Taihai Publishing House. 2017.
10. Feynman RP. Feynman lectures on physics. Shanghai: Shanghai Science and Technology Press. 2014.
11. Zheng Z. 100 Questions on relativity. Beijing: Beijing Normal University Press. 2020.