Journal of Chromatography & Separation Techniques
Open Access
ISSN: 2157-7064
ISSN: 2157-7064
Research Article - (2012) Volume 3, Issue 7
The quantitative structure–retention relationship (QSRR) was employed to predict the retention time (min) (RT) of pesticides using five molecular descriptors selected by genetic algorithm (GA) as a feature selection technique. Then the data set was randomly divided into training and prediction sets. The selected descriptors were used as inputs of multi-linear regression (MLR), multilayer perceptron neural network (MLP-NN) and generalized regression neural network (GR-NN) modeling techniques to build QSRR models. Both linear and nonlinear models show good predictive ability, of which the GR-NN model demonstrated a better performance than that of the MLR and MLP-NN models. The root mean square error of cross validation of the training and the prediction set for the GR-NN model was 1.245 and 2.210, and the correlation coefficients (R) were 0.975 and 0.937 respectively, while the square correlation coefficient of the cross validation (Q2 LOO) on the GR-NN model was 0.951, revealing the reliability of this model. The obtained results indicated that GR-NN could be used as predictive tools for prediction of RT (min) values for understudy pesticides.
Keywords: Pesticides; Quantitative structure–retention relationship; Genetic algorithm; Multiple linear regression; Retention time (min); Artificial neural networks
Pesticides with highly toxic effects, essential for agricultural production, include insecticides, acaricides, fungicides, herbicides, synergists, etc., and varieties and quantities of them used in different parts of worldwide. Due to their widespread use, pesticides need to be determined in various environmental, such as soil, water and air [1,2]. Owing to the toxicity of pesticides, the US Environmental Protection Agency (EPA) and the European Union (EU) have included them in their list of priority pollutants [3,4]. Thus, the development of reliable methods for systematic environmental analysis of pesticides residues is an important field of research. A wide range of analytical techniques has been developed for their identification of these contaminants often present at trace levels in environmental samples. The most frequently used methods for analysis of pesticides in natural ecosystems, water and foodstuffs are high performance liquid chromatography (HPLC) [5-7] and gas chromatography (GC) [8,9] with a varity detection system. For human consumption, which, as a consequence of persistency and toxicological effects of these micro-contaminants, has become in the last decades an essential aspect of environmental protection and human health safeguard policy [10,11].
An important property that has been extensively studied in quantitative structure property relationship (QSPR) [12] is the chromatographic retention time. The chromatographic parameters are expected to be proportional to a free energy change that is related to the solute distribution on the column. Chromatographic retention is a physical phenomenon that is primarily dependent on the interactions between the solute and the stationary phase. There are many reports on the application of QSRR in studying the retention properties of different compounds in various chromatographic systems [13-25].
In recent years ANNs [22,23] have gained popularity as a powerful chemometric tool that can be used to solve chemical problems [26-29]. Compared to classical statistical analysis, ANN-based modeling does not require any preliminary knowledge of the mathematical form of the relationships between the variables. This makes ANN suitable for the analysis of data where a hidden nonlinearity or a complex interdependency among the variables is present. QSRR methodology aims at describing chromatographic behavior of solutes in terms of their structure and has been extensively applied for over two decades to several chromatographic systems [24-31]. It provides a promising method for the estimation of the retention properties based on the descriptors calculated from the molecular structure [12-20,26-32]. The main steps of a QSRR study include: data collection, molecular descriptors calculation and selection, correlation model development and model evaluation. The advantage of QSRR lies in the fact that the descriptors used to build the models can be calculated from the structure alone, and once a reliable model is built.
The main aim of this work was to establish a new QSRR model for predicting the RTs (min) of some pesticides in liquid chromatography using the GA variable selection method and the generalized regression neural network (GR-NN) technique. The performance of this model was compared with those obtained by MLR and multilayer perceptrons neural network (MLP-NN) techniques.
Equipment and software
A pentium (R) Dual core personal computer (CPU E2180 2.00GHz) with the Windows XP operating system was used. Dragon software (Ver. 3.0) (http://www.disat.unimib.it/chm.) was used for calculating molecular descriptors from molecular geometries which had been previously generated and optimized by means of the Hyperchem program (Ver. 7.0). Statistical investigation of the data has been performed mainly by the Statistica 7.1 software [33]. The GA toolbox in MATLAB 7 (http://www.isis.ecs.soton.ac.uk/isystems/kernel/) was used for selecting the appropriate descriptors.
Data set and descriptor generation
The data set for this investigation was taken from the literature [34]. A complete list of the compounds’ names and their corresponding RTs (min) are summarized in table 1. Chromatographic separation was performed at 40°C on an Atlantis dC18 column, 150 mm×2.1 mm, 3 μm particle. Detection and quantification were performed with an AB API3000 LC-MS-MS equipped with an ESI Turbo Ion Spray source. The chemical structures of 43 molecules in the data set were drawn with Hyperchem software. Then obtained structures were preoptimized by using MM+ molecular mechanics force field, and then a further precise optimization was done with the AM1 semi-empirical method. The molecular structures were optimized using the Polak–Ribiere algorithm until the root mean square gradient was 0.01. The Dragon software was used to calculate the descriptors and 1243 molecular descriptors, from 18 different types of theoretical descriptor, were calculated for each molecule. In this case, to reduce redundancy in the descriptor data matrix, correlation of the descriptors with each other and with the RTs of the molecules was examined and collinear descriptors (i.e. r>0.9) were detected. Among the collinear descriptors, those with the highest correlation with RTs were retained and the others were removed from the data matrix. The remaining descriptors were collected in a 43×443 data matrix (X), where 43 and 443 are the number of compounds and descriptors, respectively. In order to obtain practical QSRR models, the significant descriptors should be selected from these molecular descriptors.
| No | pesticide | Mor07p | Mor28m | H6m | MLOGP | C005 | RT(exp) (min) | RT (MLR) (min) | RT(MLP-NN) (min) | RT(GR-NN) (min) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1* | Aminocarba | 1.29 | 0.02 | 0.02 | 2.38 | 3.00 | 2.39 | 13.49 | 14.86 | 12.34 |
| 2 | Butoxycarboxim | 0.46 | -0.01 | 0.02 | 0.26 | 2.00 | 3.78 | 8.69 | 7.19 | 8.11 |
| 3 | Oxamyl | 0.63 | 0.11 | 0.05 | 0.35 | 4.00 | 4.00 | 7.37 | 5.83 | 8.50 |
| 4* | Methomylb | 0.21 | 0.13 | 0.03 | 0.87 | 2.00 | 4.79 | 11.08 | 10.21 | 10.24 |
| 5 | Vamidothion | 0.45 | -0.09 | 0.08 | 0.74 | 3.00 | 6.53 | 8.54 | 6.97 | 8.72 |
| 6 | Ethiofencarbsulfon | 0.77 | -0.19 | 0.05 | 0.31 | 2.00 | 7.87 | 8.05 | 6.89 | 8.28 |
| 7 | Pirimicarb | 1.18 | 0.12 | 0.02 | 1.91 | 4.00 | 8.32 | 11.04 | 10.52 | 8.67 |
| 8 | Dimethoate | 0.23 | -0.03 | 0.07 | -0.76 | 3.00 | 9.74 | 5.17 | 4.49 | 7.98 |
| 9 | Thiofanoxsulfone | 1.12 | -0.05 | 0.07 | 0.91 | 2.00 | 10.03 | 11.32 | 10.31 | 10.80 |
| 10 | Butocarboxim | 0.61 | -0.06 | 0.01 | 1.60 | 2.00 | 12.40 | 11.37 | 12.45 | 11.92 |
| 11 | Triacloprid | 1.93 | -0.01 | 0.05 | 1.37 | 0.00 | 13.06 | 16.33 | 16.40 | 17.09 |
| 12 | Aldicarb | 0.41 | -0.20 | 0.08 | 1.60 | 2.00 | 13.52 | 11.18 | 12.19 | 11.32 |
| 13* | Spiroxaminea | 2.21 | -0.11 | 0.02 | 3.29 | 0.00 | 14.68 | 19.80 | 17.00 | 19.24 |
| 14 | Fenpropimorph | 2.86 | 0.03 | 0.06 | 3.83 | 0.00 | 14.95 | 23.63 | 20.78 | 18.80 |
| 15 | Demeton-s-methy | 0.29 | 0.16 | 0.00 | 1.35 | 2.00 | 16.00 | 12.13 | 12.56 | 13.01 |
| 16 | Propoxur | 2.28 | 0.04 | 0.01 | 2.38 | 1.00 | 17.23 | 17.24 | 17.85 | 18.55 |
| 17 | Bendiocarb | 3.07 | 0.16 | 0.01 | 1.88 | 1.00 | 17.53 | 17.78 | 18.67 | 18.35 |
| 18 | Dioxacarb | 2.61 | 0.22 | 0.02 | 1.34 | 1.00 | 17.54 | 16.76 | 17.98 | 17.83 |
| 19 | Carbofuran | 3.09 | 0.16 | 0.01 | 2.27 | 1.00 | 17.56 | 18.79 | 19.70 | 18.66 |
| 20 | Carbaryl | 2.12 | 0.09 | 0.03 | 3.03 | 1.00 | 18.57 | 19.41 | 20.39 | 19.26 |
| 21 | Atrazine | 1.31 | -0.14 | 0.08 | 1.77 | 0.00 | 18.95 | 16.25 | 16.77 | 17.16 |
| 22* | Ethiofencarba | 1.56 | 0.07 | 0.02 | 2.92 | 1.00 | 19.21 | 18.16 | 19.44 | 18.95 |
| 23* | Isoproturonb | 2.12 | 0.13 | 0.04 | 2.39 | 2.00 | 19.29 | 16.84 | 19.02 | 18.16 |
| 24 | Metalaxyl | 2.82 | -0.01 | 0.08 | 1.91 | 2.00 | 19.30 | 16.00 | 17.01 | 17.91 |
| 25 | Pyrimethanil | 2.36 | 0.08 | 0.00 | 2.63 | 0.00 | 19.38 | 19.62 | 18.40 | 19.09 |
| 26 | Diuron | 1.07 | 0.23 | 0.33 | 2.65 | 2.00 | 19.44 | 23.05 | 19.15 | 21.24 |
| 27* | 3,4,5-Trimethacarbb | 1.68 | -0.02 | 0.06 | 2.92 | 1.00 | 20.09 | 18.37 | 19.64 | 18.93 |
| 28 | Isoprocarb | 2.52 | -0.07 | 0.06 | 2.92 | 1.00 | 20.10 | 18.73 | 18.95 | 19.27 |
| 29 | Methiocarb | 1.40 | 0.15 | 0.08 | 3.19 | 2.00 | 21.96 | 18.95 | 21.80 | 19.48 |
| 30 | Linuron | 1.03 | 0.43 | 0.30 | 2.65 | 2.00 | 22.31 | 24.02 | 21.34 | 22.44 |
| 31 | Promecarb | 1.95 | -0.00 | 0.02 | 3.20 | 1.00 | 22.63 | 18.60 | 18.83 | 19.25 |
| 32 | Iprovalicarb | 3.29 | 0.03 | 0.12 | 3.18 | 0.00 | 22.71 | 23.80 | 22.65 | 21.24 |
| 33 | Azoxystrobin | 4.86 | 0.12 | 0.25 | 2.07 | 2.00 | 22.85 | 22.78 | 24.49 | 23.88 |
| 34 | Cyprodinil | 2.46 | 0.13 | 0.02 | 3.16 | 0.00 | 22.98 | 21.80 | 20.57 | 19.58 |
| 35 | Fenoxycarb | 3.91 | 0.11 | 0.12 | 3.18 | 0.00 | 24.60 | 25.01 | 24.05 | 21.83 |
| 36 | Metolachlor | 2.99 | 0.12 | 0.20 | 3.03 | 1.00 | 24.71 | 23.79 | 24.97 | 23.63 |
| 37* | Tebufenozidea | 3.98 | -0.01 | 0.09 | 3.95 | 0.00 | 25.48 | 25.40 | 21.69 | 20.82 |
| 38 | Haloxyfopmethy | 3.24 | 0.27 | 0.29 | 2.86 | 1.00 | 28.29 | 26.81 | 27.06 | 27.38 |
| 39 | Indoxacarb | 4.94 | 0.39 | 0.33 | 3.17 | 2.00 | 28.49 | 29.49 | 29.75 | 28.24 |
| 40* | Quizalofop-ethylb | 3.72 | 0.23 | 0.08 | 2.81 | 0.00 | 29.06 | 24.26 | 24.48 | 23.17 |
| 41 | Haloxyfop-2-ethoxyethyl | 3.01 | 0.39 | 0.23 | 2.76 | 0.00 | 29.58 | 27.71 | 28.28 | 29.27 |
| 42 | Furathiocarb | 3.12 | 0.37 | 0.22 | 3.42 | 2.00 | 30.27 | 26.00 | 27.83 | 28.17 |
| 43* | Fluazifop-butyla | 4.25 | 0.25 | 0.23 | 3.32 | 0.00 | 30.76 | 29.12 | 28.53 | 28.55 |
*Prediction set
a:Test set
b:Validation set
Table 1: Experimental retention times of 43 pesticides.
Genetic algorithm for variable selection
Genetic algorithm (GA) [35,36] is a stochastic optimization method inspired by evolution theory. It was used to select the most appropriate molecular descriptors for developing a reliable predictive model. To select the most relevant descriptors, the evolution of the population was simulated [37-40]. Each individual of the population, defined by a chromosome of binary values, represented a subset of descriptors. The number of genes on each chromosome was equal to the number of the descriptors. The population of the first generation was selected randomly. A gene was given the value 1 if its corresponding descriptor was included in the subset; otherwise, it was given the value zero. The number of the genes with a value of unity was kept relatively low to maintain a small subset of descriptors [41]. As a result, the probability of generating zero for a gene was set at least 60% greater than the probability of generating unity. The operators used here were crossover and mutation. The probability of application of these operators was varied linearly with generation renewal (0–0.1% for mutation and 70– 90% for crossover). The population size was varied between 50 and 250 for different GA runs. A population size of typically 200 individuals was chosen, and evolution was allowed over, typically, 50 generations. For a typical run, evolution of the generations was stopped when 90% of the generations took the same fitness. The best selected descriptors for building QSSR models are shown in table 2. The five most significant descriptors selected by GA are: moriguchi octanol water partition coefficient (MLOGP), H autocorrelation of lag 6/weighted by atomic masses (H6m), 3D-MoRSE signal 07/weighted by atomic polarizability (Mor07p), 3D-MoRSE signal 28/weighted by atomic masses (Mor28m) and CH3X (C005). Detailed explanations about the descriptors were found in the Handbook of Molecular Descriptors [42]. These descriptors encode different aspects of the molecular structure and were applied to construct QSRR models. Table 2 represents the correlation matrix among these descriptors.
| Mor07p | MLOGP | H6m | C005 | Mor28m | |
|---|---|---|---|---|---|
| Mor07p | 1.000 | ||||
| MLOGP | 0.557 | 1.000 | |||
| H6m | 0.433 | 0.306 | 1.000 | ||
| C005 | -0.587 | -0.584 | -0.018 | 1.000 | |
| Mor28m | 0.430 | 0.351 | 0.306 | -0.032 | 1.000 |
Table 2: The correlation coeffcient matrix for the selected descriptors by GA.
Multiple linear regressions (MLR)
MLR is a technique used to model the linear relationship between a dependent variable y (here retention time) and one or more independent variables xi, i.e., molecular descriptors as follow:
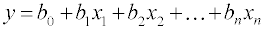 (1)
(1)
The coefficients vector b is calculated using descriptor matrix X, containing an additional column with ones to calculate coefficient b0, according to the following equation:
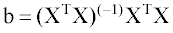 (2)
(2)
It is worth noting that MLR is based on least squares, i.e., the model is fitted such that the sum of squares of differences of experimental and predicted values is minimized. About 80% of the data set was randomly selected as training set and the remaining 20% was used as prediction set in multiple linear regression modeling. This 20% data set was divided into validation and test set for ANN modeling.
Artificial neural network (ANN)
ANNs are inspired from the information-processing pattern of the biological nervous system [43]. Input, hidden and output layers are the main components of an artificial neural network. The input layer takes information directly from input files, and the output layer sends information directly to the outside world through computer or any other mechanical control system. There may be many hidden layers between input and output layers.
We processed our data with different ANNs looking for a better model. To build an ANN model, the general tasks include training ANN, testing ANN and validating ANN. The advantage of ANN is the inclusion of nonlinear relations in the model. In this study, ANN calculations were performed with Statistica 7.1 by intelligent problem solver (IPS) and by customizing the number of neurons (from 5 to 15) with a single or two hidden layer. This program can search automatically for the optimal type/architecture of ANN. The optimization process was performed on the basis of validation error minimization. For ANN modeling, the dataset was separated into three groups: training, test and validation sets. Training task is of the most fundamental importance to build ANN models in which the observed values of the output variable is compared to the network output, and then the error is minimized by adjusting the weights and biases. It is noteworthy that the training set was the same as that of MLR model, and the molecules in validation and test sets were just identical with those selected as prediction set in MLR model. The number of compounds in the training, validation and test sets was 34, 4, and 5, respectively, and the compounds of each set were randomly selected. The neural networks were trained using the training subset only. The validation subset was used to keep an independent check on the performance of the networks during training, with deterioration in the validation error indicating over-learning. If over-learning occurs, the network will stop training the network and restore it to the state with minimum validation error. The test set was used to make sure that the validation error was not artificial. The network model will generalize if the validation and test errors are close together. The optimal network architecture was determined by ISP, which builds and selects the best models from linear (LIN), multilayer perceptron (MLP) with linear output neuron as well as generalized regression neural networks (GR-NN).
Model validation
Model validation is a crucial step of QSRR modeling. The calibration and predictive capability of a QSRR model should be tested through model validation. The most widely used squared correlation coefficient (R2) can provide a reliable indication of the fitness of the model, thus, it was employed to validate the calibration capability of a QSRR model. For validation of the predictive capability of a QSRR model, there are two basic principles: internal validation and external validation. The cross validation (CV) is a most commonly used method for internal validation. A good CV result (Q2) often indicates a good robustness and high internal predictive ability of a QSRR model. The statistical external validation can be applied at the model development step, in order to determine both the generalizability of QSRR models for new chemicals and the true predictive power of model, by properly employing a prediction set for validation [30-33]. The internal predictive capability of a model was evaluated by cross validation coefficient (Q2) using the following equation:
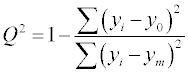 (3)
(3)
Also, the root mean square error of cross validation (RMSECV) was employed to evaluate the performance of developed models which was calculated from the following equation:
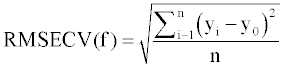 (4)
(4)
where yi is the experimental values, y0 is the predicted values, ym is the mean of observed values and n is the number of molecules [43,44].
Multiple linear regressions (MLR)
The MLR model was built through a step-wise regression by using following descriptor subsets: MLOGP, H6m, Mor07p, Mor28m and C005. The built model was used to predict the external prediction set. The statistical characteristics of MLR model using five descriptors were listed in table 3 and the predicted values for all the pesticides were given in table 1. According to the criteria for a good model mentioned above, the MLR model using five descriptor chosen by GA method had satisfactory predictive ability. The resulting equation including the selected descriptors is as follows:
| No | Descriptor | Group | Coefficient | Std. error | t-value |
|---|---|---|---|---|---|
| 1 | Mor07p | 3D-MoRSE descriptors | 0.969 | 0.604 | 1.604 |
| 2 | MLOGP | Molecular properties | 2.389 | 0.740 | 3.229 |
| 3 | H6m | GETAWAY descriptors | 19.913 | 6.901 | 2.885 |
| 4 | C005 | atom-centred fragments | -1.568 | 0.654 | -2.399 |
| 5 | Mor28m | 3D-MoRSE descriptors | 8.462 | 4.655 | 1.818 |
Table 3: Molecular descriptors employed for the proposed MLR model.
RT=10.327 (± 4.655)+2.389 (± 0.740) MLOGP+19.913 (± 6.901) H6m–1.568 (± 0.654) C005+8.462 (± 4.655) Mor28m 0.969 (± 0.604) Mor07p (5)
N=34, R=0.916, Q=0.894, F=167.043, S=3.105
The plot of experimental vs. predicted RTs (min) by MLR were shown in figure 1.
Multilayer perceptron neural network (MLP-NN)
In order to explore the nonlinear relationship between RTs and the selected descriptors, ANN technique was used to build models. The parameters such as the number of nodes for hidden layer, learning rate, and momentum were optimized using the validation set. The ability to generalize the model was evaluated by an external test set.
Taking the above-mentioned values as the reference the investigation of optimal non-linear network were under taken initially limiting the scope of search to the MLP networks [45]. The statistical results of the MLP-NN 5:5-5-1:1 network is shown in table 4 and the predicted RTs values for all the pesticides were given in table 1. The errors of the trained MLP-NN network are at least two orders of magnitude smaller than the respective errors generated by the linear network. Figure 2 confirms the good quality of the constructed MLP-NN, by showing the relationship between the predicted and experimental retention values. Figure 3A depicts the network map for MLP-NN 5:5-5-1:1 network with five inputs, five neurons in the first layer, five neuron in second layer (hidden layer), one neuron in third layer and one output.
| Model | Data set | QLOO2 | RMSECV | R | F |
|---|---|---|---|---|---|
| MLR | Training | 0.800 | 2.835 | 0.916 | 167.043 |
| Prediction | 2.615 | 0.913 | 35.037 | ||
| MLP-NN | Training | 0.947 | 1.479 | 0.950 | 294.777 |
| Validation | 1.365 | 0.969 | |||
| Test | 2.353 | 0.918 | |||
| Prediction | 2.597 | 0.925 | 46.563 | ||
| GR-NN | Training | 0.951 | 1.245 | 0.975 | 329.924 |
| Validation | 1.463 | 0.966 | |||
| Test | 2.084 | 0.950 | |||
| Prediction | 2.210 | 0.937 | 48.614 |
Table 4: Statistical results of the MLR and ANN models.
Generalized regression neural networks (GR-NN)
The model that enables the prediction of properties of chemical compounds, and which, based on the topological and quantum-chemical properties of their molecules, is by no doubt one of the more difficult and more complex models. Therefore, during modeling various types of neural networks were (experimentally) assessed, including Generalized Regression Neural Network (GR-NN) networks, which are considered in the literature as particularly predisposed to dealing with such complex problems [46-48].
The process of building the GR-NN network model is divided into two steps [49-51]. In the first step, in the space of the input signals, groups of similar cases are localized. This stage is realized using the radial layer of the GR-NN network. In the second stage, the regression approximation of the searched relationship is formed. Based on the earlier input space division by radial layer and the degree of similarity of the considered input signal to particular class, the decision is made and the result is obtained. The quality of the work of the GR-NN 5:5-34-2-1:1 network is shown in table 4 and the predicted values were given in table 1. Figure 3B shows the architecture of this neural network with five inputs, five neurons in the first layer, 34 neuron in second layer (first hidden layer), two neuron in third layer (second hidden layer), one neuron in fourth layer and one output. The scatter plot of experimental vs. predicted values of RTs (min) calculated by this model was shown in figure 4. It was evident that the predicted values agreed well with experimental values.
The statistical results of ANN models including MLP-NN and GR-NN were listed in table 4, and all the results were in accordance with the criteria for a good predictive model. According to this result, it can be seen that the quality of the GR-NN network is better than the quality of the MLR and MLP-NN. In order to compare the MLR model with ANN, the validation and test set in ANN models were evaluated together. The better results of ANN models than MLR model as shown in table 4 demonstrated the complexity of chromatography retention process. Obtained results reveal the reliability and good predictivity of the ANN models for predicting the RTs for understudy pesticides. Figure 5 shows the plot of residuals vs. experimental RTs (min) for GR-NN model. The residuals were equally distributed on both sides of zero line which indicates that no symmetric error exists in the development of our GR-NN as the best model.
Molecular descriptors
The statistical parameters of MLR model constructed by these descriptors are shown in table 2. Among them, the lipophilicity parameter MLOGP represents the extent of hydrophilic/hydrophobic interactions [52]. The positive coefficient of MLOGP indicates that an increase in MLOGP, result in an increase in RTs values. Another descriptor is H6m, which was weighted by atomic mass and is belong to the GETAWAY descriptors [53]. GETAWAY descriptors are based on the representation of molecular geometry in terms of an influence matrix (H-GETAWAY) or influence-distance matrix (R-GETAWAY). The Molecular Influence Matrix (H) is defined as:
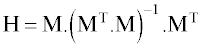 (6)
(6)
where M is the molecular matrix constituted by the centered cartesian coordinates and the superscript T refers to the transposed matrix. The diagonal elements hij of the H matrix, called leverage, encode atomic information and are considered to represent the effect of each atom in determining the whole shape of the molecule. For example mantle atoms always have higher hij values than atoms near the molecule center. Moreover, the magnitude of the maximum leverage in the molecule depends on the size and shape of the molecule itself. The Influence-distance matrix (R) involves a combination of the elements of H matrix with those of the Geometric Matrix.
The mean effect of descriptor H6m has a positive sign (Table 3), which reveals that the RT (min) is directly related to this descriptor. Hence, it was concluded that by increasing the molecular mass the value of this descriptor increased, caused to RTs of pesticides in LC increased.
Mor07p and Mor28m are the other descriptors, appearing in these models and belong to the 3D-MoRSE descriptors [53,54]. The 3D-MoRSE descriptor is calculated using following expression:
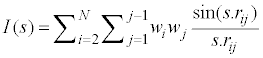 (7)
(7)
where S is scattering angle, rij is interatomic distance between ith and jth atom, wi and wj and are atomic properties of ith and jth atom, respectively, including atomic number, masses, van der Waals volumes, Sanderson electronegativities, and polarizabilities. Mor07p and Mor28m display a positive sign, which indicates that the RTs are directly related to these descriptors.
Finally, descriptor C005 is one of the Ghos–Crippen atom-centred fragments related to the methyl group attached to any electronegative atom (O, N, S, P, Se, halogens) fragment. It gives information about the number of predefined structural features in the molecule. It has shown negative influence on the prediction of RT-values (min). For this reason, RT (min) values for understudy pesticides are inversely related to this descriptor.
In conclusion, QSRR models for estimating the RT (min) were developed for a series of 43 pesticides by employing the MLR, MLP-NN, and GR-NN modeling approaches. Starting from the same set of descriptors included in the best MLR model, more robust models were obtained by the nonlinear methods of ANNs. The results obtained by GR-NN model were compared with those obtained by MLR and MLP-NN models. The results demonstrated that GR-NN model was more powerful in predicting the RTs (min) of the pesticide compounds. A suitable model with high statistical quality and low prediction errors was eventually derived.