If you ask a biologist, a chemist or a physician to enunciate the Second Law of Thermodynamics (SLT), you probably will get different answers. Besides the famous and synthetic statement “the entropy of an isolated system never decreases” [1], several other empirical formulations will be provided, such as those by Clausius, “No process is possible whose sole result is the transfer of heat from a cooler to a hotter body” [1], and Kelvin-Planck, “No process is possible whose sole result is the absorption of heat from a reservoir and the conversion of this heat into work” [1]. Although these definitions may appear conceptually distant from each other, they represent different faces of the same physical principle, as their equivalence can be easily demonstrated [1].

In many other cases, answers to your question will focus on more formal statements. The Clausius-Duhem inequality is perhaps the most popular formal statement of the SLT. It applies to thermodynamic processes during which a system evolves from one equilibrium state (A) to another (B). It asserts that the integrated heat absorbed by the system, divided by the temperature at which that heat is absorbed, is bounded from above by the net change in the entropy of the system:

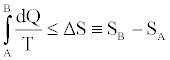− Equation 1

By “thermodynamic process”, we have in mind a situation in which the system is brought into thermal contact with a sequence of heat reservoirs at different temperatures, one at a time, while one or more external parameters of the system are varied with time producing a network. In general, the process is irreversible: it is carried out over a finite time with a finite number of reservoirs, and the system evolves, from A to B, through a sequence of non-equilibrium intermediate states. In such a case, the inequality strictly holds in Equation 1.

Macroscopic thermodynamics is essentially based on principles or postulates that are valid on empirical basis. Till now, no observation has brought to the conclusion that heat flows spontaneously from cooler to hotter bodies: therefore Clausius’ statement can be, and indeed it has been, assumed as a postulate of classical thermodynamics. However, when we move from macroscopic to microscopic world, matter could reveal aspects much more complex and bizarre than our macroscopic eyes are able to catch. These differences are dramatically evident in the outcomes of classical and quantum mechanics: from Heisenberg on, we left determinism as a natural principle, but continued to keep it for our macroscopic matters. In this respect, classical and statistical thermodynamics, as descriptions of thermodynamic events at the macroscopic and microscopic level, respectively, may present strange and intriguing differences, and indeed they do. As I will point out, their relation resembles the one existing between classical and quantum mechanics, in the sense that the former can be safely taken as a very good approximation of the latter as macroscopic processes are considered.

Important aspects of thermodynamics emerging from a statistical microscopic analysis have been disclosed at the end of the past millennium by Christopher Jarzynski, who introduced a general nonequilibrium approach to compute free energy differences between two thermodynamic states from a series of realizations which drive the system arbitrarily far from equilibrium [2]. Specifically, the Jarzynski’s approach relies on an exact relationship between the free energy difference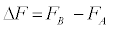 [3] and the work W performed on a system in a series of non-equilibrium realizations that switch the system from state A to state B:\

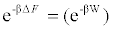Equation (2)

where 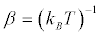kB being the Boltzmann’s constant, and the average is performed on a virtually infinite ensemble of realizations of the switching process. Note the conditions for the validity of (Equation 2) there is only one heat reservoir and its temperature T must equal that at which the system is initially prepared. Equation 2 has been derived in a number of ways, and confirmed in single-molecule experiments [4]. This result just represents a statistical steady statement of the SLT. More surprisingly, it contains the classical expression of the SLT which involves the free energy difference, namely 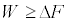. In fact, by exploiting the convexity of the function ex in Equation 2, i.e., 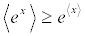, we obtain

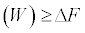Equation (3)

Which is the SLT in the statistical sense? Thus, the work averaged over all possible realizations of a process, rather than the work performed in a single realization of the process, is always greater than, or equal to, ΔF. This means that, for a single realization, the statement 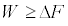can be violated! Strictly speaking, we cannot talk about a SLT for a single transformation; because it is defined only for a statistical ensemble of realizations of a process (see Equation 3 with its equalitybased form Equation. 2 and next Equation 6 with its equality-based forms Equations 4, 5).

Now, can we say something about the Clausius-Duhem inequality? There exist a statistical statement of it? The answer to this question was given by Jarzynski himself in [5], where he proposed an extension of Equation. 2 to a process in which the system can be put into contact with several thermal baths during irreversible transformations, the first and the last bath being at the temperatures TA and TB, respectively:

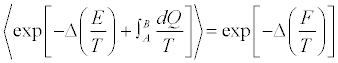Equation (4)

Here, as in Equation 2, the average is estimated from an infinite number of realizations leading the system from A to B, reversibly or irreversibly does not matter. In Equation. 4,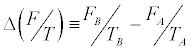 and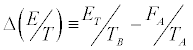 where E₀ and E_τ denote, respectively, the initial and final internal energies of the system. Note that, while 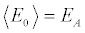[6] because the initial microstates of the realizations are picked from an equilibrium distribution, for the final state the inequality 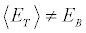holds, as the microstates at the end of the irreversible realizations are not required to be canonically distributed. Only if we leave the system in thermal contact with the bath at TB at the end of each realization (till reaching equilibrium), then the equality 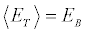holds. Exploiting the identity 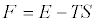into Equation 4 gives

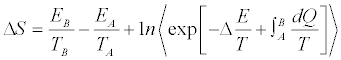(5)

This result expresses the entropy difference 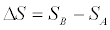in terms of an arbitrary, in general irreversible, thermodynamic process from A to B. In principle, by repeatedly measuring E0, Eτ, and B / 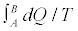for independent realizations of such a process, we can construct the averages appearing in Equation 5, and therefore compute the value of ΔS. This is in my opinion the most general statement of the SLT, as it is valid independently on the fact that the system is or is not left to relax at equilibrium. Applying the convexity of the function ex in Equation 5 and supposing to left the system to relax at equilibrium after each realization which implies 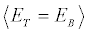, we get

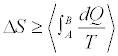Equation (6)

This result says, effectively, that the Clausius-Duhem inequality is satisfied “on average”, where the average is taken over an ensemble of realizations of a given thermodynamic process. This still leaves open the possibility that there exist individual realizations for which the inequality is violated. This is indeed true!

In summary, if the strict form of the Clausius-Duhem inequality (Equation 1) does not hold for a single microscopic or macroscopic transformation, but only for an infinite collection of transformations (Equation 6), must classical thermodynamics textbooks supplemented with errata? The Publishers should not worry about. They are saved from the empirical observation that the probability of violating the Clausius-Duhem inequality is practically (but not in principle!) zero as macroscopic transformations are concerned. In fact, the probability of observing a violation of the Clausius-Duhem inequality, by an amount no less than T, is bounded from above by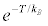 [5]. A macroscopic violation would be one for which 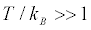, hence such violations are extremely rare: the Clausius-Duhem inequality is “never” violated by a macroscopic amount.

Just to understand better the situation, let’s consider the problem from a slightly different perspective. Suppose to estimate the difference 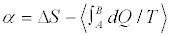for an ensemble of macroscopic irreversible transformations, exploiting Equation 5 to compute ΔS. In such a case, on the basis of Equation 6, we would get a positive value for α. At the same time, the quantity 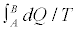would be distributed around its mean value with a given dispersion, say γ. The basic point here is that for macroscopic irreversible processes 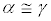, so that no fluctuation in the 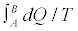quantity can actually violate the SLT. Instead, for microscopic processes, such as those occurring in single-molecule manipulation experiments [4], we do observe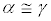so that violations of the SLT are not only possible, but even highly probable. These two situations are schematically represented in the Figure 1.

Figure 1: Representation of the distributions of the quantity 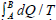obtainable from realizations of generic macroscopic and microscopic processes (left and right panels, respectively). In macroscopic processes, α >>γ and hence no violations to the SLT are actually observed (a virtually infinite number of realizations should be performed to observe a violation). Instead, in microscopic processes, α ≡γ : SLT violations can be observed much more easily!

In conclusion, what about Clausius’ and Kelvin-Planck’s statements for macroscopic systems? Only a light restoration.

“It is extremely improbable (practically impossible) to observe a macroscopic process whose sole result is the transfer of heat from a cooler to a hotter body” (Clausius).

“It is extremely improbable (practically impossible) to observe a macroscopic process whose sole result is the absorption of heat from a reservoir and the conversion of this heat into work” (Kelvin-Planck).

Note the two additions: the sentence “It is extremely improbable” and the adjective “macroscopic”. A general definition of the SLT cannot however disregard from using the cool mathematical language of Equation 4. Or, if you prefer, the equivalent Equation 5.

Beyond this report, the interested Readers can find stimulating discussions in [7].