Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
+44 1300 500008
ISSN: 2157-7544
+44 1300 500008
Research Article - (2018) Volume 9, Issue 2
In this paper, we obtained exact analytical solutions for the nonstationary linear inverse heat conduction problem for bodies of one-dimensional geometry with boundary conditions on one surface, obtained in a closed recurrent form. The recurrent form of the solution of a nonstationary linear inverse heat conduction problem for bodies of onedimensional geometry with boundary conditions on one surface given in the article is a solution in closed form from unified positions, which is not always possible in explicit form.
Keywords: Thermal conductivity; Analytical; Non-stationary; Linear; One-dimensional; Inverse problem; Surface; Border conditions; Recurrent
Urgency of application of reversal tasks of heat conductivity and heat exchange
Direct mathematical modeling allows predicting the thermal state of a wide range of operating modes, for example, a technical system, analyzing the influence of various factors on the behavior of this system and choosing the optimal thermal conditions.
The use of direct methods of mathematical modeling requires an analysis of the accuracy of mathematical models. A model can have a very complex structure and consider a sufficiently large number of factors. However, it is necessary to set the numerical values of all the characteristics of the model the thermophysical properties of materials, characteristics of thermal interaction with the washing medium, etc. If the information is missing or has low accuracy, then the complex mathematical model loses its advantages and does not provide the required forecast accuracy thermal modes.
The practical application of mathematical modeling of heat transfer shows that the possible unsatisfactory accuracy in mathematical modelling, for example, of high-intensity thermal processes, is due to the low accuracy of characterization using traditional direct methods. In such cases, the use of computational-experimental methods that are based on the principles of identification of systems with distributed parameters, which are based on algorithms and methods for solving various types of incorrect inverse heat transfer problems, may be very effective. As is known, in direct problems the temperature field is sought, which is found as a solution to the heat equation with known internal transport parameters corresponding to known boundary and initial conditions, and in inverse heat conduction problems the initial temperature distribution and boundary conditions are unknown functions to be defined.
Inverse tasks are divided into two main types:
• Determination of the parameters of internal energy transfer - coefficients of heat and thermal diffusivity, heat capacity, light absorption coefficients, etc., which are the physical characteristics of the substance;
• Determination of the conditions of external energy exchange between the body and the medium, i.e., finding boundary conditions: this includes calculating the temperature of the outer surface and the heat flux passing through it, calculating variable heat transfer coefficients, thermal contact resistances, degrees of blackness, angular irradiation coefficients, phase transition or destruction surface positions, compilation of nonstationary balances of power and energy, etc.
To obtain a solution to the inverse heat conduction problem is much more complicated than the direct one; however, in a direct problem, many obstacles of an experimental nature may arise in measuring or realizing the specified boundary conditions. Physical conditions are, for example, such that it is not always possible to install the sensor on the surface of the body or the measurement accuracy is significantly reduced due to the placement of the sensors. Therefore, it is often difficult to measure the law of temperature variation of the heated surface of a solid. It is much easier to perform accurate measurements of the temporal dependences of temperature at internal points on the thermally insulated surface of the body. Thus, the problem arises of choosing between relatively inaccurate measurements and a complex analytical task. At the same time, a sufficiently accurate and easily realizable solution of the inverse problem would simultaneously reduce both difficulties to a minimum.
The direct problem of heat conduction under correctly set conditions has a unique solution. In the case of inverse problems, the identity of temperature fields is possible as a result of different external effects in terms of their nature, but energetically equivalent. The temperature field of a solid body does not determine uniquely the boundary conditions under which it arose. Several energetically equivalent in their effects on the system g.The boundary conditions can reflect complex temperature processes in different ways.
An example is the fact that any redistribution of heat flux densities, for example, between convective and radiation components, when combined, leads to the identical thermal state of the system [1]. There are also other drawbacks inherent in the inverse methods of studying non-stationary heat exchange in technical systems: limiting the number of points in the details in which temperatures and heat fluxes are measured; Experimentally determined temperatures and heat fluxes, on the basis of which calculations are made, contain measurement errors even when using precision instruments, since the placement of sensors in a solid body to some extent violates the temperature field of the parts; surface curvature, spatial and temporal variation of heat fluxes in the body do not make it possible to accurately predict the direction of heat flux, or in other words, determine the location of the sensor, which should be on the normal to the surface.
It should be noted that inverse methods do not allow the physical interpretation of non-stationary complex processes occurring in systems. In addition to the disadvantages, including the above, inverse methods have several advantages compared with direct ones. In a direct problem, many obstacles of an experimental nature may arise when measuring or realizing specified boundary conditions. Physical conditions in the studied systems may be such that it is impossible to install the sensor on the body surface (for example, on the surface of coatings) or the measurement accuracy is significantly reduced due to the placement of sensors, therefore it is often difficult to measure the law of temperature and heat flux changes of solid surfaces.
Summarizing the above, we can conclude that there is an urgency in obtaining in a single form an exact closed analytical solution of the nonstationary linear inverse heat conduction problem for bodies of one-dimensional geometry with boundary conditions on one surface. In this article, an exact closed analytical solution to this inverse heat conduction problem is achieved in a recurrent form, i.e., in an implicit form, since it is not possible in all cases in an explicit form [2-6].
Solutions in the recurrent form for nonstationary linear reverse problem of heat conduction for bodies of one-dimensional geometry with boundary conditions on one surface
The existing exact solutions of the inverse problems of unsteady heat conduction are relatively few, and they are significantly less than the corresponding solutions of the direct problem of unsteady heat conduction. It can be pointed out that one of the first successful attempts to solve the inverse problem of unsteady heat conduction for a flat body was first undertaken in 1890 by J. Stephan.
Subsequently, for a one-dimensional linear inverse nonstationary heat conduction problem, solutions were obtained in an independent way by O. Burggraf and D. Langford if the nonstationary heat flux density and temperature are known at the sensor location. Exact solutions for temperature fields using previously known temperatures at two different internal points using the Laplace integral transform method were obtained by M. Imber and D. Khan.
Similar solutions for one-dimensional bodies are also given in and, in which solutions for non-stationary temperatures are given explicitly, and the heat flux density is determined by the differentiation of temperature fields.
Later, solutions of similar problems were obtained, partly having not only theoretical, but also applied nature, including the nonlinear onedimensional problem of unsteady heat conduction [7-19].
As partly indicated in, the expression of solutions for the nonstationary linear inverse heat conduction problem for bodies of one-dimensional geometry in explicit form is not possible in all cases, therefore, in order to obtain a final solution, additional assumptions must be applied, for example, as in where the thin wall assumption is used.
The purpose of this article is to obtain a solution to the nonstationary linear inverse heat conduction problem for bodies of one-dimensional geometry with boundary conditions on one surface from uniform positions in a closed recurrent form, which will have certain advantages in explicit form because they can be obtained for all the above problems, and explicitly not for everyone.
Fill in the equation of nonlinear unstable stationary thermal conductor production for the body of one geometry and constant curvature (in this case we consider the radial coordinate):
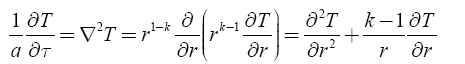 (1)
(1)
where k is the number of final measurements: 1 is a flat field; 2 - cylindrical; 3 - spherical; T is the temperature; r is the radial coordinate; a - temperament coefficient thermal diffusivity.
The domain of definition of the differential equation (1) is from 0 to r2 (radial coordinate of the outer surface) along the coordinate (in the case of hollow bodies: from r1 (radial coordinate of the inner surface) to r2) and from 0 to the current value over time (τ>0).
In a dimensionless form, this equation can be written as follows:
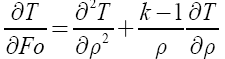 (2)
(2)
where 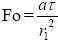 is the Fourier criterion; ρ=r/r1 is the dimensionless coordinate; r1 is the radial coordinate on which the boundary conditions are specified.
is the Fourier criterion; ρ=r/r1 is the dimensionless coordinate; r1 is the radial coordinate on which the boundary conditions are specified.
The inverse problem of heat conduction for equation (1) or (2) is to find the boundary conditions on the surface of a one-dimensional body at known unsteady temperature and heat flux and the thermophysical characteristics of the material of the body that do not depend on temperature.
In this article, the process of heat conduction is studied at a time sufficiently remote from the initial moment of time, therefore the influence of the initial conditions has practically no effect on the temperature distribution at the time of measurement or observation (the so-called "task without initial conditions"). In practical terms, this may mean that with an enough distance from the initial moment of time, the aftereffect component, which takes into account the influence of the initial conditions, becomes so small that it is already less than the measurement error of the sensors measuring temperatures and heat fluxes.
The component of the influence of the temperature field of a one-dimensional layer, which is heated on the inner surface, is considered using a dimensionless coordinate, for which the heated surface corresponds to a single value (the homo chronicity complex refers to this inner radial coordinate) can be represented as follows:
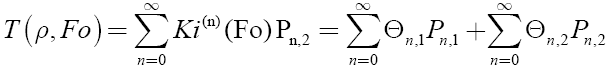 (3)
(3)
where 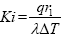 Kirpichev criterion;
Kirpichev criterion; 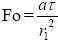 is the Fourier criterion; ρ=r/r1 is the dimensionless coordinate; r1 is the radial coordinate on which the boundary conditions are specified; a - coefficient of thermal diffusivity; λ is the coefficient of thermal conductivity; q is the heat flux density; ΔT is the temperature difference.
is the Fourier criterion; ρ=r/r1 is the dimensionless coordinate; r1 is the radial coordinate on which the boundary conditions are specified; a - coefficient of thermal diffusivity; λ is the coefficient of thermal conductivity; q is the heat flux density; ΔT is the temperature difference.
On the heated surface a boundary condition of the second kind takes place. In this case, the heat flux density and temperature are measured on the same surface.
Solutions for bodies of simple configuration will differ in the values of the radial quasi polynomials Рn,1 and Рn,2. In the framework of this work, these quasi-polynomials will be solved in recurrent forms.
Body planar geometrical shape: The quasi-polynomials Pn,1 and Pn,2 for a flat plate will be as follows:
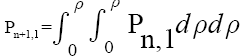 (4)
(4)
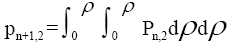 (5)
(5)
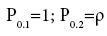 (6)
(6)
For the first quasi-polynomials Р1,1 and Р2,1 etc., Р1,2 and Р2,2 etc. for a flat plate you can write:
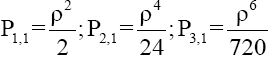 (7)
(7)
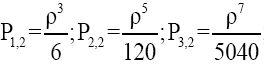 (8)
(8)
Consequently, using the method of mathematical induction, one can write quasi-polynomials for solving an inverse nonstationary heat conduction problem when specifying the boundary conditions on the same surface for a flat plate in a recurrent form:
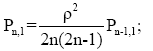 (9)
(9)
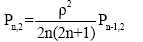 (10)
(10)
Continuous cylinder: The quasi-polynomials Pn,1 for a solid cylinder will be as follows:
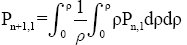 (11)
(11)
P0.1=1 (12)
For the first quasi polynomials Р1,1 and Р2,1 etc. for a solid cylinder can be written:
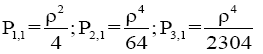 (13)
(13)
Consequently, using the method of mathematical induction, one can write quasi-polynomials for solving an inverse nonstationary heat conduction problem when specifying the boundary condition on the axis of the continuous cylinder in recurrent form:
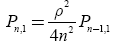 (14)
(14)
Hole cylinder: The quasi-polynomials Pn,1 and Pn,2 for a hollow cylinder will be as follows:
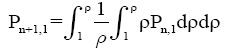 (15)
(15)
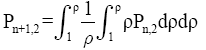 (16)
(16)
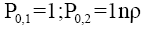 (17)
(17)
For the first quasi polynomials Р1,1 and Р2,1 etc. for hollow cylinder, you can write:
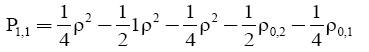 (18)
(18)
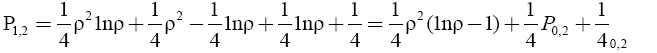 (19)
(19)
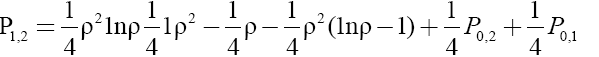 (20)
(20)

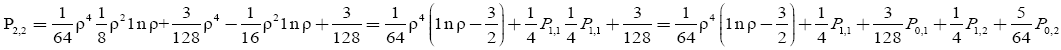 (21)
(21)
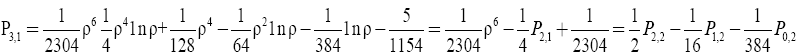 (22)
(22)
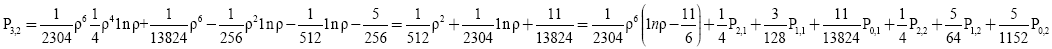 (23)
(23)
Cquently, using the method of mathematical induction, one can write quasi-polynomials for solving an inverse nonstationary heat conduction problem when specifying the boundary condition on the inner surface of a hollow cylinder in a recurrent form:
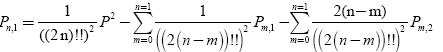 (24)
(24)
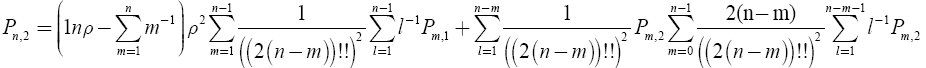 (25)
(25)
Continuous ball: The quasi-polynomials Pn,1 for the solid ball will be as follows:
 (26)
(26)
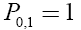 (27)
(27)
For the first quasi polynomials P1,1 etc. for a solid ball can be written:
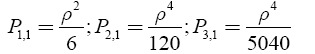 (28)
(28)
Consequently, using the method of mathematical induction, one can write quasi-polynomials for solving an inverse nonstationary heat conduction problem when specifying the boundary condition at the center of a solid ball in recurrent form:
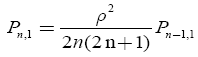 (29)
(29)
Hole ball: The quasi-polynomials Pn,1 and Pn,2 for a hollow ball are as follows:
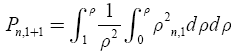 (30)
(30)
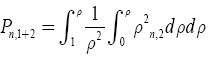 (31)
(31)
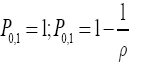 (32)
(32)
For the first quasi polynomials Р1,1 and Р2,1 etc. for a hollow ball you can write:
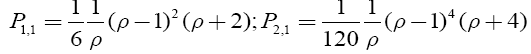 (33)
(33)
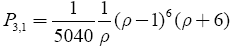 (34)
(34)
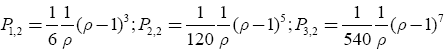 (35)
(35)
Therefore, using the mathematical method Consequently, using the method of mathematical induction, one can write quasi-polynomials for solving an inverse nonstationary heat conduction problem when specifying the boundary condition on the inner surface of a hollow ball in a recurrent form:
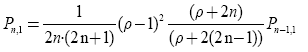 (36)
(36)
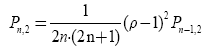 (37)
(37)
For given nonstationary boundary conditions ɵn,1 and ɵn,2 the recurrence relations will be as follows:
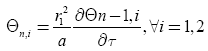 (38)
(38)
The above relations express the recurrent form of the exact solution of the inverse problem of non-stationary heat conduction for bodies of onedimensional geometry with non-stationary boundary conditions specified on one side.
The recurrent form of the solution record makes it possible to solve this problem from a unified position in a closed form, since the expression of solutions is explicit, perhaps not in all cases.
Questions of the correctness of this inverse problem of heat conduction (i.e., the existence of a solution, its uniqueness and its stability) were considered therefore, in this study there is no need to re-examine them.
The above-mentioned solutions of the nonstationary inverse heat conduction problem for one-dimensional bodies obtained above were successfully applied in practical terms as an integral part of the conjugate problem in determining the maximum effect of a deposit on the surface of the combustion chamber on the nonstationary parameters of the working fluid during radiative-convective heat transfer [20-22] also when developing the theory of heat transfer in insulating packaging to stabilize the temperature regimes of storage of perishable products.
For the heat exchange conditions calculations were performed for the dependencies generated in this paper. With the same temperature boundary condition, the largest deviation will be for a flat body, and the smallest - for a solid sphere; for a solid cylinder there will be an intermediate value. For both the hollow cylinder and the hollow ball, the temperature deviation will be greater than for the solid cylinder and ball, respectively. A comparison of a hollow cylinder with a hollow ball shows that for small values of r2/r1 the deviation for a hollow cylinder will be less than for a hollow ball, but for large values of r2/r1 the deviation for a hollow cylinder will be larger than for a hollow ball. For the conditions under consideration [23,24], the above fracture occurs at a value of r2/r1 ≈ 3 2/15. Analysis of the performed calculations indicates a stronger dependence of the calculated temperature on the parameter r2/r1 for a hollow ball than for a hollow cylinder.
• The urgency of the problem of solving the inverse linear non-stationary heat conduction problem of a one-dimensional geometric shape, obtained in this work in a closed recurrent form, is that it is possible to restore the boundary conditions by an enough degree of accuracy by measuring the heat flow sensor.
• In this paper, we obtained exact analytical solutions for the nonstationary linear inverse heat conduction problem for bodies of onedimensional geometry with boundary conditions on one surface, obtained in recurrent form.
• The recurrent form of the solution of the nonstationary linear inverse heat conduction problem for bodies of one-dimensional geometry with boundary conditions on one surface obtained in the article is a closed-form solution from a unified position, which is not always possible in explicit form.
• From a practical point of view, the solutions obtained can be used in the calculation of non-stationary temperature fields and heat flux densities for various materials used in aviation and rocket-space technology, based on the measured non-stationary boundary conditions on one of the sides.