Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2009) Volume 2, Issue 2
Differential proteome analyses focus on the detection and quantification of expression changes between samples from different biological groups. While the significance of an expression change is detected by some statistical test, the strength of an expression change is usually quantified by some ratio estimate, e.g. the ‘fold change’. Due to its quantitative character, the fold change is more intuitively for biologists than the decision of a statistical test. However, strong expression changes are often misleading if this change is not significant. For this reason, we propose the employment of confidence intervals, adjusted for multiple hypotheses testing, which naturally comprise both, test decision and quantification. The adjusted confidence intervals can be used for making test decisions under the control of error rates typically considered in multiple hypotheses testing (e.g. the familywise error rate or the false discovery rate). For biologists, test decisions based on adjusted confidence intervals offer a more intuitive method for selecting proteins with a significant expression change between two groups. The length of the intervals can be used for sample size planning of upcoming experiments. Our approach is primarily addressed to protein expression data recorded by two-dimensional Difference Gel Electrophoresis.
Keywords: Differential proteome analysis, Confidence intervals, Multiple hypothesis testing, 2-Dimensional Difference Gel Electrophoresis.
2-DE: Two-Dimensional Gel Electrophoresis; DIGE: Difference Gel Electrophoresis; WER: Family-Wise Error Rate; FDR: False Discovery Rate.
Typically, a differential proteome study is performed for comparing samples from distinct biological groups, each consisting of several individuals. Stühler et al., (2006) for example compared pairwise the brain proteome of mice from groups of different developmental stages, embryonic, juvenile and adult. Another experimental design is the comparison of proteome samples from several individuals before and after treatment. Differences in the proteome of a neuroblastoma cell line before and several hours after stimulation with a nerve growth factor were for example studied by Sitek et al., (2005). The common goal of such studies is to detect candidate proteins involved in relevant biological pathways or as drug targets co-regulated with the examined biological groups or with the applied treatments. Here, we consider particularly the case of two independent groups.
The application of two-dimensional gel electrophoresis (2- DE) means to compare the expression levels from thousands of proteins and their post translational modified species simultaneously. 2-DE is an important tool for measuring protein expression levels by separating proteins by their isoelectric point and molecular size (Klose and Kobalz, 1995). Being covalently labelled by a fluorescent dye or silver-stained before and after separation, respectively, the proteins are revealed as distinct spots on the 2-D gels, where intensity of a spot can be taken as a measure of abundance. The image of each gel is digitized by a scanner and spots are detected by an automatic image analyzing algorithm.
An improvement of 2-DE is two-dimensional Difference Gel Electrophoresis (2-D DIGE), which allows to analyze up to three distinct proteome samples, labelled by three different fluorescent dyes (Cy2, Cy3 and Cy5), within the same gel (Ünlü et al., 1997). Usually, these three samples are one observation from the treatment group, one from the control group and one is an internal standard. Consequently, equal group sizes are normally used in such an experimental set-up. The internal standard is a mixture of the proteome samples from all individuals involved in the experiment. It is used to standardize the recorded expression levels of the treatment and control group and making thus the separate gels comparable. A 2-D DIGE gel in the described setup yields three different digital images, which are obtained using different emission wavelengths for scanning, specifically for each of the dyes. In this article we specifically regard data from the 2-D DIGE technique, though our approach is also applicable to protein expression levels recorded by other quantitative proteome techniques. In order to match the spot maps of the individual gels, one master gel is selected (which is representative for the experiment) and all spot maps from the other gels are matched to the spot map of the master gel. Because not all protein spots that were detected on the master gel are found in the other gels the effective sample size is different for single proteins (Jung et al., 2005; Jung et al., 2006).
Significant expression changes between treatment and control sample are usually detected by classical t-tests in 2- D DIGE experiments. While the p-values resulting from these tests can be taken as a measure of significance, they do not provide quantitative information and are often not intuitively comprehensible for non-statisticians. For this reason, besides detecting statistical significance of expression changes by t-tests, the strength of those changes is usually quantified by some ratio estimate, e.g. the ‘fold change’. If the ratio is greater than one, the protein is called up-regulated and it is called down-regulated if the ratio falls below one. It is a common practice in proteomics studies to pre-select proteins for further laboratory analyses not only by test decisions, but also by the magnitude of the ratio. However, the applied thresholds for these ratios are mostly unjustified values. For instance, it has been suggested to utilize two times the standard deviation of an in-gel analysis (DIA, Difference in Gel Analysis) as the threshold for the determination of significant expression changes (Karp et al., 2004). Furthermore, these ratio estimates can be misleading by suggesting a strong expression change for a certain protein, while the variance of this ratio is also very high and the expression change is thus not significant. Hence, a ratio of for example 1.5 can have different accuracy and does not necessarily mean that the respective protein is truly up-regulated. Thus, making a test decision by using a confidence interval instead of the p-value, gives on the one hand not only the information for rejection or non-rejection of the null hypothesis, but relativizes the view to the simple fold change on the other hand.
Therefore, we propose here to make use of the general duality between test and confidence interval. A confidence interval is generally defined as a region that covers the true parameter with probability (1 – α). If one quantifies the strength of the expression changes by confidence intervals, one can call a particular protein significantly up-regulated if the lower confidence limit exceeds one and down-regulated if the upper limit falls below one. This has the benefit of testing and quantifying at the same time.
Searching for differentially expressed proteins means to perform thousands of tests simultaneously. If the individual significance level for each test is for example α = 5%, a high number of false positive findings is to be expected in many cases. In fact, if the individual significance level for each test is α = 5%, the global significance level α* increases by 1 – (1 – α)n, where n is the number of individual tests (Lehmann, 1986). Thus, the global significance level α*, i.e. the probability for making a false test decission becomes nearly equal 1 if the number n of tests is just one hundred. Therefore, certain error rates are usually controlled in multiple hypothesis testing, e.g. the false discovery rate (FDR) or the more strict family-wise error rate (FWER). These error rates can for example be controlled by adjustment algorithms for the raw p-values of the tests. Test decisions based on adjusted p-values result in smaller portions of false positive findings than those based on the raw p-values. Here, in a two-step algorithm, we firstly calculate such adjusted p-values for finding an adjusted α- level, and secondly use this α-level for calculating the confidence intervals. Thus, the test decisions based on the confidence intervals are also under control of the chosen error rate. Whereas the duality between test and confidence interval is a natural fact in statistical test theory, and p-value adjustments for certain error rates are already widely used, a combination of both for analyzing high-dimensional data has not yet been used within the field of proteomics.
This paper is organized as follows: In the next section we present our experiment, formalize the data structure resulting from 2-D DIGE experiments and detail the adjustment of confidence intervals. In the subsequent section we present the results of a 2-D DIGE study, analysing a lung adenocarcinoma cell line A549 upon TGFβ treatment applying our method. At the end we give a discussion of our method and the results.
Data Acquisition: 2D-DIGE Analysis of a Cellular Model for Lung Fibrosis
In order to collect a data set, large enough for in depth statistical analysis, we choose a cellular model for lung fibrosis. By stimulating the well established lung adenocarcinoma cell line A549 (Giard et al., 1973) with the growth factor TGFβ we hope to additionally get insights in the process of TGFß signal transduction and secondary cellular effects. TGFb is known to be a mediator of multiple processes in lung tissue like wound repair, inflammatory processes, senescence or survival of certain cell populations. In our 2-D gel based approach we compared TGFβ stimulated with non-stimulated cells: we used cell lysates prepared from 40 independent culture dishes – 20 for each group (TGFβ treated and untreated). Expression levels of these samples were measured by the use of 2D-DIGE gels (method described by Sitek et al., 2005). For this 50 µg of cell lysates were labelled with fluorescence dyes (TGFß treated: Cy3; untreated: Cy5; internal standard – a mixture of all samples: Cy2), combined and separated in two dimensions (Klose and Kobalz, 1995). Subsequently the 20 produced gels were scanned using the Typhoon 9400 scanner (GE Healthcare) and three images per gel acquired representing the three different Cy-dye channels resulting in 60 spot map images.
Before image analysis with the DeCyder 2D 6.5 software (GE Healthcare) the images were cropped with ImageQuantTM software (GE Healthcare). The intra-gel spot detection was performed using the Differential In-gel Analysis (DIA) mode of the DeCyder software. The estimated number of spots was set to 10,000. An exclusion filter was applied to remove spots with a volume value < 20,000. The DeCyder BVA module has been used for spot matching and quantitation of spot volume data. The software algorithm first applies a normalization procedure resulting in normalized spot volumes for each spot map. Based on these normal volumes, standardization was performed by building ratios between the Cy3 and Cy2 channel (internal standard) and Cy5 and Cy2 channel respectively of each spot pair. The resulting normalized and standardized spot volumes were used for further calculations: the mean volumes of matched spots were calculated for each group and provided the basis for building spot volume ratios.
Adjustment of Confidence Intervals
We begin this section with a short scheme of the data structure resulting from a 2-D DIGE experiment. Let n be the total number of protein spots detected on the master gel and the individual spots themselves be indexed by j (j = 1,..., n). As mentioned before, not each spot detected on the master gel is found on all other gels and available sample sizes mj are thus different for the individual spots. For spot j, mj denotes the number of gels were this spot has been detected by the automatic image analysis algorithm. The expression levels for spot j can be denoted by xj = (xj1,...,xjmj) for the treatment group and by yj = (yj1,...,yjmj) for the control group. We re-emphasize that the available sample size mj of each spot is the same in both groups, because missing spots ‘occur’ always simultaneously in a 2-D DIGE experiment in the used setup.
In the following, we assume that xj and yj represent already pre-processed expression levels, i.e. they are normalized, standardized and log-transformed.
A typical measure which is often used for estimating the expression change of a particular protein j is called the ‘fold change’ Rj. For protein j it is defined by:
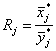 (1)
(1)
where X¯ *jand Y¯ *jare the geometric means of the expression levels in the treatment and control group, respectively, before log-transformation. Thus, a fold change of 2 means a 2-fold up-regulation in the treatment group, whereas a fold change of 0.5 means a 2-fold down-regulation. For better interpretation, fold changes less than one are often represented as their negative reciprocal.
For assessing the significance of a protein’s expression change, Welch’s t-test is usually used in the analysis of such 2-D DIGE experiments. The null hypothesis of this test is that there is no difference between the means of the logtransformed expression levels of the two groups. A confidence interval for this difference is given by
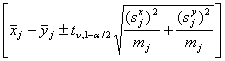 (2)
(2)
where X¯j, Y¯j,Sxj and Syj are the means and standard deviations in the two groups tv1-α/2 and is the (1 – α / 2)- quantil of the t-distribution with
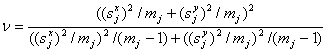 (3)
(3)
degrees of freedom (Moser and Stewens, 1992). Simple confidence intervals for the fold change can now be obtained by exponentiating the confidence limits in equation (2). Instead of making a test decision by the p-value of the t-test, one can use these confidence intervals for deciding whether a protein is significantly differentially regulated: a significant up-regulation is given if the lower bound exceeds one, and a significant down-regulation is given if the upper confidence bound falls below one.
Testing each of the several thousand proteins with an individual significance level of α = 0.05 may possibly result in a large number of false positive test decisions. Therefore, an adjustment of p-values with respect to some error rate is common. Two special error rates that are often desired to be controlled in multiple hypothesis testing are the familywise error rate (FWER) and the false discovery rate (FDR). The FWER is defined as the probability of having at least one false positive. This error rate can be controlled by the Bonferroni-correction, which is either made by performing each test with an adjusted significance level of αBonf =α / n, i.e. the individual significance level divided by the number n of tests, or by adjusting the raw p-value Pj of protein j by
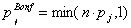 (4)
(4)
and comparing PBonf jwith the unadjusted α-level. Either procedure guarantees an FWER of α.
A less strict error rate is the FDR, which is defined as the portion of false positives among all positive test decisions.For controlling the FDR, p-values can be adjusted by the procedure of Benjamini and Yekuteli (Benjamini and Yekuteli, 2001), which should particularly be used if a correlation between variables is obvious. This procedure starts by sorting the raw p-values in an ascending order: P1?P2?....Pn. The adjusted p-values are than given by
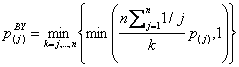 (5)
(5)
(Dudoit et al., 2003). Assume now that k proteins have an adjusted p-value pBY smaller than α. Instead of using these adjusted p-values one can also compare the raw p-values against an adjusted α-level αBY = α × k / c, where
c=∑nj-1 1/j,for making a test decision.
The adjustment of the confidence intervals in equation (2) with respect to the FWER or the FDR is simply given by exchanging the raw α-level by αBonf or by αBY.
Automatic image analysis of our gels, without user interferences, carried out by the DeCyder software, results in 3359 protein spots on the master gel. Because not all spots from the master gel were detected in all gels, different available samples sizes for the 3359 proteins were obtained (Fig. 1). For the further analyses we included only those 3149 spots that have a sample size of at least five observations.
Figure 1: Distribution of the available samples sizes of the altogether 3359 detected protein spots. 325 spots have been detected in all 20 gels of the experiment, 317 have been detected in 19 of these gels, and so on. About 28% of all spots have been detected in only 10 or less gels, about 8% in 5 or less.
For detecting differentially regulated proteins we first performed a two-sample t-test for each spot using individual a-levels of 0.05 resulting in a total of 1916 differentially regulated proteins. According to their fold change, 948 of them are up-regulated and 968 are down-regulated. In order to reduce the number of false positives we adjusted the raw p-values according the method of Benjamini and Yekuteli to obtain an FDR of 5%, yielding 1447 differentially regulated proteins, 679 of them up-regulated and 668 down-regulated. The stricter FWER-adjustment yields 388 up-regulated and 359 down-regulated proteins.
Next, instead of using the p-values for making a test decision, we derived the unadjusted and adjusted confidence intervals, detailed in the method section, and called a protein significantly up-regulated if the respective lower confidence limit exceeded one, and called it down-regulated if the respective upper confidence limit fell below one. Due to the duality of test and confidence interval, these procedures, in the unadjusted and in the two adjusted cases, yield the same sets of up- and down-regulated proteins as the p-valuebased test decisions. i.e., the lower limit of an up-regulated protein exceeds one exactly when the related t-test p-value falls below 0.05 (Fig. 2). Reversed, the upper limit of a downregulated protein falls below one, when the related p-value falls below 0.05. Thus a test decision can also be made based on the confidence intervals instead of using the pvalues. It is a fact that many non-statisticians do not realy know how to interpret the p-value. It is however very easy to understand that a spot is up-regulated if the lower limit of a confidence interval for the fold change exceeds one.
Figure 2: t-Test p-values versus lower and upper limits of the confidence intervals. a) Significantly down-regulated proteins: the upper limits fall below one exactly when the p-values are below 0.05. b) Significantly up-regulated proteins: the lower limits exceed one exactly when the p-values are below 0.05, too. Both plots show the unadjusted case, but the same concordance was observed in the adjusted cases.
The lengths of confidence intervals naturally depend on the sample size (Fig. 3) and on the variance of the data. In particular, the lengths of the intervals decrease when the sample sizes increase. In our case the lengths also depends on the adjustment method. The smallest intervals were the unadjusted ones, whereas the FWER-adjusted intervals were the largest. The largest confidence interval (reaching from 0.0015 to 1045.49) in our study was obtained when using the Bonferroni-adjustment, where the samples size for the associated protein was mj = 5. The largest confidence interval when using the Benjamini-Yekuteli-adjustment reaches from 0.31 to 24.66 (associated sample size: mj = 7).
We proposed to use adjusted confidence intervals, instead of p-value based test decisions, for the detection of differentially regulated proteins observed in 2-D DIGE experiments. Test decisions based on confidence intervals and those based on p-values are naturally equivalent, so that the same sets of up- and down-regulated proteins are obtained. Adjustments can control typical error rates used in multiple hypotheses testing like the FWER or the FDR. Other typical adjustments of multiple hypotheses testing, that were not considered in this study are possible, as for example the FDR-procedure of Benjamini and Hochberg, (1995), which is based on stronger assumptions with regard to the correlation structure between the single tests. The confidence interval method was more intuitive for non-statisticians and allows easier biological interpretations. It is a fact that many proteome scientists overestimate the relevance of proteins with a high fold change without considering the statistical significance of an expression change. However, proteins with the same fold change can have a completely different significance. Table 1 presents two proteins with a fold change of about 1.5. The corresponding confidence intervals showed that the protein with rank 1363, depending on the type of adjustment, can not necessarily be seen as differentially expressed. In particular, that protein with the largest positive fold change (Rj = 2.79) in our experiment is not statistically significant (raw p-value = 0.09, see also Figure 5).
| Rank (According t-tests) |
Raw p-Value |
Fold Change | Confidence Interval (Unadjusted) | Confidence Interval (FDR) | Confidence Interval (FWER) | Sample Size |
| 1 | 9.7 * 10-24 | 0.59 | [0.57, 0.62] | [0.55, 0.64] | [0.53, 0.66] | 20 |
| 2 | 2.7 * 10-23 | 1.93 | [1.82, 2.05] | [1.75, 2.12] | [1.66, 2.23] | 20 |
| 3 | 4.7 * 10-23 | 0.58 | [0.55, 0.61] | [0.53, 0.63] | [0.51, 0.66] | 20 |
| 47 | 8.3 * 10-15 | 1.51 | [1.43, 1.59] | [1.38, 1.64] | [1.31, 1.73] | 19 |
| 1363 | 2.7 * 10-03 | 1.51 | [1.17, 1.95] | [0.99, 2.30] | [0.78, 2.95] | 13 |
| 2067 | 9.1 * 10-02 | 2.79 | [0.79, 5.19] | [0.36, 11.30] | [0.07, 62.35] | 8 |
Table 1: Fold changes as well as unadjusted and adjusted confidence intervals for a selection of proteins. Ranks are assigned with respect to statistical significance. If a confidence interval for the fold change includes the 1, there is no statistical evidence that the associated spot is differentially regulated. Adjustments according to the FDR (false discovery rate) or the FWER (family-wise error rate) reduce the number of false positive findings, where the FWER is even more strict than the FDR.
Figure 5: 2D-DIGE analysis of cell lysates of TGFß treated and untreated A549 cells. A) Overlay of Cy3 (green, TGFß treated) and Cy5 (red, untreated) channel images. Comparable spot intensities appear in yellow. B) Singel channel image of proteins harvested from TGFß-treated A549 cells. C) Singel channel image of proteins harvested from untreated A549 cells. D) 3-D view of a protein spot found to be differential between the two analysed groups, E) 3-D view of the spot with rank 2067 (see Table 1). The spot shape looks more like a stripe or smear resulting from a non-optimal spot focussing. We can exclude this ‘spot’ by our statistical analysis because even it exhibits a fold change reasonable for highly differential expression (fold change 2.79) the differentially expression lacks statistical significance.
The length of a confidence interval depends always on the available sample size. Therefore, this method can also be used for sample size decisions for upcoming studies, by choosing an appropriate degree of precision for the quantification of the expression changes. Especially for the most significant proteins, the length is rather small, and therefore the expression change unambiguous (Table 1).
Before calculating t-tests and confidence intervals, expression levels were normalized, standardized and logtransformed. Normalization is usually done for removing dye-specific gains in the raw expression levels. This can for example be done by normalization methods used in DNA microarray experiments (Bolstad et al., 2003). Standardization is performed by dividing all values from the treatment and control group by the corresponding values of the internal standard. This pre-processing step is needed for making the distinct gels comparable. The last step in pre-processing is usually a log- or asinh-transformation for stabilizing the variance, which has been found to depend on the mean value of a spot (Kreil et al., 2004).
A lack of our analysis is the normality assumption that is made by the t-tests and the confidence intervals. Furthermore, we assume that there is still a bias between detected and true fold change. Bolstad, (2004) detected such a bias in the analysis of gene expression data recorded by DNA microarrays.
At the end of this article we want to give a short biological discussion of our experiment. We detected a large number of differentially expressed proteins, even when using the strict Bonferroni adjustment. This can be traced back to the fact that TGFβ induced changes affect many different groups of proteins (Derynck and Akhurst, 2007). The cells change their morphology and their growing characteristics. So proteins of the cytoskeleton, energy and metabolic pathways as well as proteins of different signalling networks are affected which present a huge part of the cells’ total proteome. Indeed, a high portion of differences in untreated and TGFβ-treated A549-cells was also detected on the RNA level by Keating et al., (2006). Additionally, many of the differentially regulated proteins show only a small expression change and are not necessarily biologically relevant. The distribution of their fold changes is displayed in Figure 4. 551 of the 747 protein found with the Bonferroni adjustment have an absolute fold change higher than 1.3, 251 an absolute fold change higher than 1.5 and only 35 of them have an absolute fold change higher than 2.0.
Figure 4: Distribution of the fold changes of the 747 differentially regulated proteins between TGFb treated and untreated samples, found with the Bonferroni adjustment of p-values and confidence intervals (fold changes smaller than one are represented as their negative reciprocal). For up-regulated proteins, the lower limit of the confidence interval for their fold change exceeded one, and for down-regulated proteins, the upper limit fell below one.
Currently a software, called Statistical DIGE Analyzer, for the analysis of data from 2-D DIGE experiments is being developed at the Medizinisches Proteom-Center. This software will include the methods proposed in this article.
This work was supported by the Ministry of Innovation, Science, Research and Technology North Rhine Westphalia “Ziel 2-Programm NRW 2000-2006” (grant PtJAZ0511V01 and Nachwuchsgruppe Neuroproteomics) and ProDaC. ProDaC is funded by the European Commission (6th framework programme, project number LSHG CT 2006