Advances in Automobile Engineering
Open Access
ISSN: 2167-7670
ISSN: 2167-7670
Research Article - (2015) Volume 4, Issue 2
This paper presents the first experimental and computational investigation into the
aerodynamics
of emergency response vehicles and focuses on reducing the additional drag that results from the customary practice of adding light-bars onto the vehicles’ roofs. A series of wind tunnel experiments demonstrate the significant increase in drag that results from the light bars and show these can be minimized by reducing the flow separation caused by them. Simple potential improvements in the aerodynamic design of the light bars are investigated by combining Computational Fluid Dynamics (CFD) with Design of Experiments and metamodelling methods. An aerofoil-based roof design concept is shown to reduce the overall aerodynamic drag by up to 20% and an analysis of its effect on overall fuel consumption indicates that it offers a significant opportunity for improving the fuel economy and reducing emissions from emergency response vehicles. These benefits are now being realised by the UK’s ambulance services.
<Keywords: Vehicle aerodynamics, Wind tunnel, CFD, Fuel economy, Shape optimization
CAD: Computer Aided Design; CFD: Computational Fluid Dynamics; DoE: Design of Experiments; ERV: Emergency Response Vehicle; HGV: Heavy Goods Vehicle; OLH: Optimal Latin Hypercube
Moving road vehicles induce a range of complex aerodynamic flow features including separation bubbles, edge and horseshoe vortices, separating shear layers and eddying turbulent wake structures [1]. Each of these contributes significantly to the overall aerodynamic drag and the trend for ever increasing fuel prices and more stringent environmental legislation has provided strong incentives for reducing them in order to improve fuel economy and reduce emissions. Since Heavy Goods Vehicles (HGVs) consume a disproportionate share of overall fuel consumption (in the UK for example, over 20% of the total fuel consumption is spent by HGVs which make up only 1.3% of all vehicles [2]) there has been a particular focus on reducing their fuel consumption through improved aerodynamic design [3].
Aerodynamic drag of HGVs is usually reduced through a number of approaches including streamlining airflow [4], reducing the extent of wake and flow separation regions and covering exposed underbody structures. Cab roof fairings, which aim to streamline the flow from a cab to a trailer are the most common retrofit [5] however trailer-front fairings [6] and boat tails and base flaps [7] have also been shown to be useful. More advanced methods such as boundary layer control techniques have also been studied on HGVs [8].
Although the complexity of road vehicle aerodynamics means that wind tunnel and road testing remain indispensable components of practical road vehicle aerodynamic design projects [9], the number of studies which are using Computational Fluid Dynamics (CFD) to improve the aerodynamic design of road vehicles is increasing rapidly. Examples include the drag reduction of HGVs [10-12], motorsport vehicles [13,14], and passenger vehicles [15,16]. In addition, there is growing recognition of the benefits of coupling high fidelity CFD with systematic optimization techniques for the shape optimization of vehicles. Adjoint methods for CAD-based shape optimization have recently become viable for whole vehicle optimization [17,18] and will be used increasingly within industry to reduce aerodynamic drag.
This paper addresses the aerodynamic drag reduction of vans, which are converted for use as emergency response vehicles (ERVs) to provide patient transport to hospital and within the police service in the UK. There has generally been far less research into aerodynamic improvements for vans [19], however funding constraints arising from the recent financial crisis, coupled with rising fuel prices, have forced public authorities in the UK to address the aerodynamic design of their ERVs. For example, the Yorkshire Ambulance Service Trust (YAST) fleet has 1500 ERVs travelling 40 million miles every year, resulting in the consumption of 4.2 million liters of fuel at a cost of more than £6 million. The YAST, in common with all other Ambulance Service Trusts in the UK, has ambitious targets of reducing CO2 emissions from its fleet operations (currently set at 30%), and improved aerodynamic design has been identified as a significant potential contributor to achieving substantially reduced fuel consumption and CO2 emissions.
In practice, due to a range of existing regulations, the shape of ERVs cannot be changed radically due to constraints on features such as the overall maximum vehicle height and the minimum vehicle height at the rear in order to provide adequate access to the vehicle. An additional complicating feature, which the present study shows leads to significant increases in aerodynamic drag, is the need to position warning lights at the front and rear of the roof. This paper is directed at reducing the additional aerodynamic drag caused by these light bars by streamlining and integrating them within the roof. Other parts of the vehicle (e.g. the lower surface, under-body features) are not considered.
The paper is organized as follows: The wind tunnel testing, flow visualization studies and drag measurements are described in Section 2. The CFD methodology and its validation are described in Section 3, together with a simple shape parameterization and drag reduction of a generic ERV. The results are then applied for real ambulance duty cycles to assess the potential improvements in fuel economy that could result from aerodynamic improvements. Conclusions are drawn in Section 5.
The aerodynamic drag penalty resulting from the addition of light bars was quantified by a series of wind tunnel experiments carried out using a small-scale wind tunnel in the Whitehead Aeronautical laboratory at Queen Mary, University of London. The wind tunnel has a working section cross-sectional area of 0.7 m2 (1 m × 0.7 m) and 1/8th scale ERV models are placed in it, with a frontal area of 0.066 m2, and a blockage factor of 8.5%. Experiments are carried out on a series of ERV models based on van conversions typically used by ERV fleets in the UK. The examples shown in Figure 1 are based on the Vauxhall Vivaro van design [20] and consist of (a) a standard, unconverted van, (b) a van with light bars added onto the roof and (c) a van with flat, connected light bars. The research is focused solely on the effect of the light bars; other parts of the vehicle are not considered.
Experiments were carried out for a range of different air speeds and found to be consistent. For an air speed of 26.6 m/s (60 mph), the Reynolds number, with the length scale based on the length of the ERV model, L=0.6 m, is 1.1×106. The drag force, D, was measured for all three models and 100 readings for each case were recorded at 1 second intervals; standard deviations in drag force were typically smaller than 1%. Free stream turbulence intensity was measured at 0.5% and this value was employed in all subsequent CFD comparisons. The resultant drag coefficients for all three models and air speeds, defined by
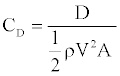 (1)
(1)
where ρ is the air density (kg/m3), A the frontal area (m2) and V the inlet air velocity (m/s) are given in Table 1. The results demonstrate that the addition of light bars typically increases CD by around 30%, however the use of flat light bars enables this increase to be reduced to around 20% (Table 1).
| Baseline model | 0.308 |
| Baseline model with light bars | 0.406 |
| Baseline model with flat light bars | 0.337 |
Table 1: Drag coefficients, CD, from the wind tunnel experiments with V=26.6 m/s.
The flow field was visualised by attaching small wool tufts to the roof and rear of the ERV models. Figure 2 shows the wool tuft disturbances that result from flow past the ERV model with and without light bars at V=26.6 m/s. Figure 2a shows that for the ERV model without light bars, the flow over the roof appears to be essentially streamlined and attached while the disturbances at the rear indicate the expected flow separation. Figure 2b shows the corresponding visualizations when the light bars are attached to the roof; the notable disturbances to the tufts behind the front and rear light bars indicate large separation regions behind them as well as the large wake at the ERV’s rear. These observations are consistent with the drag measurements in Table 1.
| Baseline ERV model | ERV model with light bars | |||||
|---|---|---|---|---|---|---|
| Grid cell count | Sk-ε | Rk-ε | Exp | Sk-ε | Rk-ε | Exp |
| Fine (~8.5 million) | 0.500 | 0.271 | 0.308 | 0.640 | 0.420 | 0.406 |
| Medium (~6 million) | 0.502 | 0.275 | 0.308 | 0.650 | 0.429 | 0.406 |
| Coarse (~4.5 million) | 0.542 | 0.285 | 0.308 | 0.680 | 0.441 | 0.406 |
Table 2: Effect of grid density and turbulence model on CD predictions at V=26.6 m/s (Sk-ε – standard k-ε, Rk-ε-realizable k-ε, Exp – wind tunnel experiments).
A more detailed study into reducing the aerodynamic drag is described further.
The aerodynamic drag reduction strategy adopted for the light bars is to combine accurate CFD modelling with a streamlined roof shape parametrization. These methods are developed and validated by comparison with data from the wind tunnel experiments.
CFD validation
A CFD representation of the wind tunnel geometry and ERV model was constructed using the commercial CFD package FLUENT [21], (Figure 3). In order to reduce the computational costs only symmetrical zero yaw angle cases are considered, enabling the flow domain to be halved. Due to the geometric complexity, a fully block-structured grid with hexahedral cells was not practical and a combination of hexahedral and tetrahedral cells were employed instead. This strategy allowed the majority of the flow domain to be discretised using structured elements.
A grid independence study was carried out by solving flow past the baseline ERV model at V=26.6 m/s on three different grids with global cell counts of approximately 4.5, 6.0 and 8.5 million. Steady state solutions were obtained by employing second order upwinding with the standard and realizable k-ε models and with standard wall functions and y+ values in the recommended range 30 ≤ y+ ≤ 300 [22]. Table 2 shows that the CFD predictions of CD on the two finest grids are effectively grid-independent and that the realizable k-ε model agrees reasonably well with experiment while the standard one is in much more poorer agreement. This is consistent with the findings of Gilkeson et al. [23] for similarly bluff vehicles (Table 2).
The effect of the light bars on the flow field for the realizable k-ε model is shown in Figure 4. These show more clearly that the increased drag results from the large separation region on the roof behind the front light bar. The aerodynamic drag study described below focusses on reducing the size of this separation region. Since many CFD simulations are needed for a comprehensive drag reduction study, all subsequent CFD results are obtained using the realizable k-ε model and a medium grid density (~6 million cells).
CFD model of the generic ERV
The drag minimization study is carried out by considering flow past a full-scale ERV in the symmetrical flow domain shown in Figure 5, which has a semi-elliptical cross-section surrounding the vehicle whose height (18.5 m), width (22.5 m) and length (85.5 m) lead to minimal blockage (0.8%) and capture the turbulent wake behind the vehicle. The boundary conditions imposed are given in Table 3. The ERV is again based on the Vauxhall Vivaro van (Table 3).
| Boundary | Boundary type | Parameters |
|---|---|---|
| Inlet | Velocity inlet | 26.6m/s |
| Outlet | Pressure outlet | 0 Pa |
| Road | Moving wall | 26.6m/s |
| Tyres | Rotating wall | 70.5 rpm |
| Vehicle surface | Stationary wall | No slip |
| Domain top | Stationary wall | Zero shear stress |
Table 3: Boundary conditions for the CFD simulations of flow past the full-scale ERV.
The drag reduction study investigates simple aerodynamic changes that can reduce the aerodynamic drag penalty which results from the addition of the light bars shown in Figure 1b.
Aerodynamic drag reduction
Shape parametrization of the light bars: It is important to choose a flexible and efficient shape parametrization scheme that can be automated and provides feasible geometries and meshes for the sequence of designs seeking to reduce aerodynamic drag. Since the main goal of this study is to establish the potential for drag reduction, a simple approach is used based on the recent aerodynamic optimization study of buses [12] that embeds the front and rear light bars into the roof. The front light bar is based on a symmetric aerofoil, where the location of the maximum thickness represents the integrated front lights, and is attached to the rear light bar which has a rectangular cross-section [24].
The aerofoil concept is shown in Figure 6 and is based on two design variables, its angle of attack, x1 degrees, and its maximum thickness fraction x2, which is non-dimensionalised with respect to its chord length, c. In order to comply with ERV regulations ensuring passenger comfort and accessibility, the rear height of the van is invariant. Preliminary investigations of the interactions of the design variables led to the following design space being investigated: 0 ≤ x1 ≤ 1.5 and 0.05 ≤ x2 ≤ 0.15. The aerofoil parametrization was based on a simple NACA 4-digit profile [25]. Its half thickness, I, as a function of the distance, x, along the chord is given by
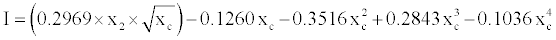 (2)
(2)
where xc=x/c. The upper contour of the aerofoil is generated using 1000 equally distributed points along its chord.
Drag reduction strategy: The objective function to be minimised within the design space 0 ≤ x1 ≤ 1.5 and 0.05 ≤ x2 ≤ 0.15 is the aerodynamic drag force D (in Newtons). The first step was to obtain a 25 point Optimal Latin Hypercube (OLH) Design of Experiments (DoE) using a permutation Genetic Algorithm which achieves uniformity of design space coverage using the Audze-Eglais potential energy criterion [26]. CFD solutions were then obtained at all 25 of the DoE points and the predicted aerodynamic drag force, D, extracted from the solutions. Metamodels (also often termed response surfaces) for D were then built using the Moving Least Squares (MLS) method [27,28] within Altair Hyperstudy [29]. This technique can cater for the noisy responses that can be encountered in vehicle aerodynamics [23]. The metamodel can be tuned by selecting an appropriate ‘closeness of fit parameter’, θ, which is contained within a Gaussian weight decay function, namely
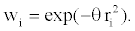 (3)
(3)
where ri is the Euclidean distance of the metamodel prediction location from the ith DoE point. High noise smoothing is achieved if θ is small whereas high values of θ lead to interpolation and little smoothing. The metamodel for D was tuned to the CFD responses using the technique developed by Toropov et al. [26], resulting in an R2 value between the CFD and MLS predictions of 0.986.
The metamodel is shown in Figure 7 and suggests that the angle of attack is the most influential design variable of the design space. It further indicates that the drag decreases monotonically with increasing angle x1 and reducing thickness x2 so that the optimum will be at the design space corner with the maximum angle x1=1.5 degrees and the minimum airfoil thickness x2=0.05 m. A CFD simulation of the flow past the ERV with streamlined light bars predicted a drag force that was within 0.2% of the value predicted by the metamodel. This design modification has a dramatic effect on the overall drag. The CFD solutions predict that the addition of light bars increases the overall drag by over 30% (from 408 N to 540 N) whereas the streamlined ones result in only a 7% increase in drag (to 437 N) compared to the baseline design without light bars. Pathlines shown in Figure 8 show how the streamlined light bars reduce separation on the vehicle roof. Reducing the vehicle height at its rear would also offer further opportunities for drag reductions [12] however practical considerations, such as the requirement of maintaining the vehicle height at its rear to facilitate easy accessibility, constrain the scope for achieving even greater drag reductions. This improved design was subsequently tested in the wind tunnel using a model fitted with the streamlined light bars. The flow visualization for inlet speed V=26.6 m/s is shown in Figure 9 and confirms that the large region of flow separation behind the light bars has been effectively removed. This resulted in an aerodynamic drag force that is only 8.6% larger than for the baseline model of Figure 1a, in good agreement with the corresponding CFD predictions described above.
Although the effect of drag reduction on the fuel economy of ERVs has not been considered previously, there is a large, highly-relevant literature on the benefits of improved aerodynamic design on the fuel economy of heavy vehicles. It has been estimated that for such vehicles approximately 60% of fuel is converted into heat, 10% due to the driveline transmission losses and 8% due to power accessories [30], with the remainder spent overcoming the total resistive force opposing vehicle motion. At higher speeds, the aerodynamic drag is mainly due to pressure drag associated with large vehicle fronts, wakes and complex underbody flow, and improved aerodynamic design can potentially make a major contribution to improving fuel economy. Pressure drag increases with the square of the vehicle speed and Wood and Bauer [31] found that for HGVs reducing fuel consumption by 1% requires a reduction in aerodynamic drag of 6% at 20 mph, however this reduces to only 2% drag reduction at 60 mph. The latter is consistent with McCallen et al. [3], who found that the percentage reduction in fuel consumption is approximately half the percentage reduction in drag for speeds in the range 40 to 70 mph. Mohammed-Kassim and Filipone [2] carried out a numerical study into the fuel saving potential of dragreducing devices retrofitted to HGVs by modelling resistive forces throughout the vehicle journey based on the fuel consumption analysis of Emmelmann and Hucho [32]. This predicted a linear relationship between the percentage reduction in aerodynamic drag force and fuel consumption and that HGVs operated on long-haul (extra-urban) routes generally save twice as much fuel as in urban areas.
The impact of aerodynamic drag reduction from the use of the streamlined light bars on fuel consumption is estimated for two duty cycles provided by the Yorkshire Ambulance Service Trust (YAST), shown in Figure 10. The first is a predominantly urban duty cycle with an average speed of 34 mph and the second is an extra-urban one with an average speed of 51 mph. Due to lack of data specific to ERVs, the following analysis is based on the methodology developed by Mohammed-Kassim and Filipone [2] for HGVs. However, this can easily be adjusted to ERV-specific performance data.
The total resistive force that has to be overcome by burning fuel is composed of aerodynamic drag together with rolling, acceleration and climbing resistances. For simplicity, the latter is neglected while the percentage of the total fuel consumed in order to overcome the acceleration resistances for the two duty cycles can be estimated from the data of Mohammed-Kassim and Filipone [2]. Aerodynamic drag is modelled by D=kV2 where k is a constant and V the vehicle speed. The values of k for the standard and streamlined light bars are matched to the aerodynamic forces predicted by the full-scale CFD analyses at V=26.6 m/s. The rolling resistance R=mg × fR, where m is the mass of the vehicle (kg) and fR is the rolling resistance coefficient, taken to be
fR=0.0041 + 0.0000917 V. (4)
where vehicle speed V is in m/s. Since the fuel lost as heat is proportional to the fuel converted into useful work and frictional losses, a reduction in any of the resistive forces results in a proportionate reduction in fuel consumption [2]. The effect of the ~19% reduction in aerodynamic drag with the streamlined light bars compared to the standard ones on the estimated percentage reduction in fuel consumption for both duty cycles is shown in Figure 11 for 2000 kg ≤ m ≤ 5000 kg. Note that the typical mass of a Vauxhall Vivaro van conversion is of the order of 3000 kg. Both the increase in vehicle mass and an urban duty cycle noticeably reduce the benefits of aerodynamic drag reduction, which is consistent with previous studies. For a 3000 kg vehicle, the ~19% reduction in aerodynamic drag leads to a 12.5% and 14.4% reduction in fuel consumption for the urban and extra-urban duty cycles, respectively. McCallen et al. [3] and Mohammed-Kassim and Filipone [2] found that for heavy vehicles (m ≥ 20,000 kg) the percentage reduction in fuel consumption is approximately half that of the percentage reduction in aerodynamic drag, so these larger predicted values are likely to be due to the smaller vehicle masses considered here. If vehicle mass is increased to 20,000 kg, the analysis used here predicts much more modest reductions in fuel consumption of 4.4% and 6.4% respectively.
Figure 12 shows predictions of how a percentage reduction in aerodynamic drag affects the corresponding reduction in fuel consumption, for vehicles of mass 3,000 kg and 5,000 kg. The linear relationship is as expected [32], while the slopes are larger than for HGVs [2]. As noted above, this is probably due to the significantly smaller vehicle mass of ERVs, however more detailed HGV-specific information of rolling resistances, mechanical and acceleration losses is required.
Rising fuel costs, coupled with the need to reduce the environmental impact of fleet operations, are stimulating interest in improving the aerodynamic design of ERVs. The experimental and computational results presented demonstrate that improving the aerodynamic design of the roof and light bars in ERV conversions offers a significant opportunity for reducing fuel consumption from ERV operations. For example reducing the fuel consumption of the YAST’s ambulances during its fleet operations by 5% would save £350,000 annually and reduce the associated carbon emissions by 250 tonnes of CO2, savings which could be extended throughout the UK’s NHS national fleet.
The present research has stimulated the commercial development of a new generation of fuel efficient ambulances. Road trials within the YAST have shown that the cumulative benefits from improved aerodynamic design, through streamlined light-bars and vehicle bodies, reductions in weight, and changes to a single wheel rear axle, enables fuel economy to be improved by between 40% and 60% [33]. It is also likely that these techniques could be used to achieve substantial improvements in fuel economy for other important types of ERVs.
The authors would like to thank the UK’s Engineering and Physical Sciences Research Council EPSRC EP/H500251/1) for funding an initial Knowledge Transfer Secondment project with the YAST and to thank Andrey Polynkin for his support and advice during an initial study from which the present paper developed. Thanks are also due to Peter Occardi (formerly from OnScene Special Vehicles Ltd) and Richard Smith, Fleet Engineering Manager from the Yorkshire Ambulance Service Trust, for their support and encouragement of this work.