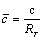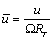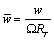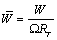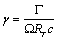The helicopter is an aircraft that uses rotating wings to provide lift, propulsion and control. The rotor lift is obtained as a reaction force by accelerating the air downward of the rotor. The blades of the rotor are maintained in uniform rotational motion, usually by the shaft torque from an engine. The lift and drag forces on these rotating wings produce the torque, thrust and other forces and moments of the rotor [1-4].

Development of lift on the rotor

In its simplest model the rotor can be considered as a rotating device capable of producing lift by drawing air from above, increasing its axial velocity and made to pass through the rotor (Figure 1). The change in the velocity of the slipstream caused by the rotor is called the induced velocity and this change results in the change of momentum of the slipstream so that a reaction to this change occurs on the rotor which is the thrust.

Figure 1: Slipstream formed by a vertical climbing rotor.

The blade is a rotating wing and as such it can be modeled by a vortex system consisting of bound vortices within the wing and free vortices coming off from the trailing edge (Figure 2). These free vortices are carried downstream by the axial velocity of the slipstream so that a helical vortex sheet formation takes place within the slipstream (Figure 3). This wake is to be modeled for the estimation of aerodynamic characteristics.

Figure 2: Vortex system of a wing (Lifting line model).

Figure 3: Helical vortex sheet trailing from a blade.

Modeling of the wake

The slipstream below the rotor has significant influence on the performance of the blade. Therefore the wake has to be modeled so that one can get a quantitative estimate of lift and torque produced by the blades, the most accurate method of calculating the performance of the blade is to model the blade as a lifting surface with its span-wise and chord-wise vortex system and the free vortex sheet emanating from the trailing edge in the form of a helical vortex system. This is called a free wake (Figure 4) analysis and calls for large computing time.

Figure 4: Free spinal vortex with wake contraction.

It may be observed from earlier studies that several models such as free spiral vortex wake model (Figure 4), vortex ring model used by Miller (Figure 5), have been proposed to predict the load distribution of helicopter rotor blades. These models even after simplification require extensive computing time. This is the purpose of this present study to explore a model that would retain the accuracy of computation and to introduce further reduction and simplicity in computing effort.

Figure 5: Vortex ring model used by miller for hovering rotor.

Description of the proposed model

In the proposed model, the blade is treated as a rotating wing of finite span. Each blade is divided into a number of segments ‘n’ in the span-wise direction (Figure 6). Each segment is represented by a bound vortex placed along the span at the quarter-chord point and chordwise vortices coming off from the ends of the bound vortex towards the trailing edge and leaving at the trailing edge as helical vortices. According to the present model those helical vortices forming the wake are replaced by two ring vortices kept below the rotor plane at a suitable location and the chord-wise vortices are connected to the ring vortices by two straight vortex filaments parallel the axis as shown in Figure 7. The radius of the vortex ring and its axial position are pre-determined. This system therefore forms the complete vortex system as it satisfies Kelvin and Helmholtz laws of vortex motion. The velocity induced by the vortex system is obtained by the application of Biot-Savart’s law to the vortex line. The contributions to induced velocities at any control point stem from all the blades of the rotor and the wake.

Figure 6: Lifting line model with bound and free vortices.

Figure 7: Vortex ring model (proposed model).

Formulation of the problem

The coordination system of the rotor blade at an instant is shown in Figure 8. The rotation of the blades is in the clock-wise direction about the x-axis, with angular velocity Ω. Each of the blades is divided into ‘n’ span-wise segments as shown in Figure 8. The relative velocity of flow with respect to a blade section is shown in Figure 9.

Figure 8: paneling of blades and helical horse shoe vortex representation of panel.

Figure 9: Flow conditional at a blade section.

Each segment is represented by a bound vortex of unknown strengthΓ_j extending along its quarter-chord line with chord-wise vortices extending from its ends to the trailing edge. Each of the vortex starting from the trailing edge is replaced by a single vortex ring of the same strength placed below and parallel to the rotor plane but with modified radius.

The induced velocity is calculated at the mid- point of each segment along the quarter-chord line due to the vortex system of the blades and the wake-vortex rings by using Biot-Savart’s law

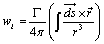
Where, 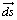is elemental length of vortex line, and 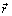the position vector directed from the element to the field point (i) where wi is required.

The Prandtl’s kinematic flow condition is fulfilled at the mid-point of the segments of the reference blade in the form,

α = α_e + α_i

Where, α is the geometrical angle of attack, which can also be expressed as

α = θ – ϕ

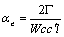
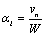
v_n = u cosϕ – w sinϕ

These equations may be expressed in non-dimensional form for the control point P₁ as

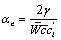
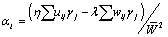
The kinetic boundary condition may therefore be expressed as

θ_i - ϕ_i = (α_e + α_i )_I Or

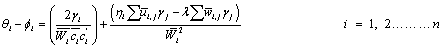
Solving this set of simultaneous equations, one can obtain the non-dimensional circulation distribution ‘γ’ along the blade. From this circulation distribution using Kutta-Joukowski theorem one can calculate the lift, induced drag for each segment of the blade and hence the thrust and torque coefficients can be obtained in the following form:

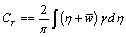
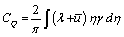
Determination of the size and location of vortex ring

The axial location of the vortex ring depends to a great extent on the geometry of the blade, particularly the chord, and the setting angle. The location was therefore expressed by a combination of these two factors by an expression namely, 0.75 c sin θ, which represents the axial displacement of a fluid particle as it moves in the chord-wise direction from the quarter-chord point to the trailing edge. Also, the induced velocity is influenced very much by the number of blades ‘B’ of the rotor. Therefore it was postulated that the axial location of the vortex ring can be expressed by the combination as

X_c = (K + B) 0.75 c sin θ

Where, K represents a constant to be determined.

The radius of the vortex ring also depends upon the radius of the point where the induced velocity is to be obtained and the radius of the blade vortex which the ring is representing. The radius of the vortex ring depends on the radius of the trailing vortex. Since the determination of the free-wake position involves larger computer time, it was postulated that this radius can be expressed by the product of the radius of the trailing vortex and the radius of the point where the induced velocity is required. Therefore, the radius of the ring has been expressed as

y_ring= K₁y_cy_j

Where the value of K₁ has been obtained by numerical experimentation using the above method and is given by

K₁= 1.0 for y_c ≤ 0.81

K₁= 0.1 for y_c > 0.81

Using these equations the circulation distribution was calculated and was found to be in good agreement with the results of other models. This formulation therefore has been adopted for different kinds of rotors with different blade geometries.

The circulation distribution obtained after solving the system of simultaneous equations shows that γ depends on the number of segments taken on each blade. Therefore, the computations are performed for determining the minimum number of segments required for estimating the circulation distribution reasonably well.

Comparison of the proposed method with other theoretical and experimental results

In order to test the validity of the proposed method, the results of the proposed method are compared with the available experimental and theoretical results. In the present case the comparison is made for a two bladed rotor of rectangular plan form with 11° twist which is due to Miller [1,2] for hovering conditions (Figure 10). For the geometrical data of the rotor, computation of the span-wise circulation distribution for a rotor with varying number of blades is obtained by the proposed method. This is shown plotted in Figure 11 for hovering. Also, carried out computations for comparison of Thrust/Torque coefficients by different models (Figure 12). It may be observed from these figures that the present simple method predictions follow closely the experimental trend and also the theoretical results.

Figure 10: Blade bound circulation distribution and location of wake vortices-straight blade.

Figure 11: Circulation distribution along the blade for hovering condition.

Figure 12: Comparision of thrust/torque coefficients by different models.

The simplified ring vortex wake model predicts the circulation distribution along the blade which is in close agreement with Miller’s experimental and theoretical results for hovering condition. The comparison was made for a setting angle of 30°. This can be generalized for any other setting angle. The results of this model agree well with the results of spiral vortex model for climbing condition also. It may be noted that no other simpler model has been found to exist in the literature for climbing condition. Further, the model is able to predict the aerodynamic characteristics of rotor without sacrificing the accuracy in spite of gross simplification of the model.

This model predicts the aerodynamic characteristics of the rotor as accurately as the spiral vortex wake model by taking considerably smaller computing time which is less than 1⁄15^th of that of other models.

The method is very simple as it involves comparatively smaller mathematical equations and take smaller amount of computer time, at the same time without sacrificing the accuracy of the results.

Therefore, this method can be recommended to calculate the aerodynamic characteristics of the rotor in hovering flight and for vertical climbing flight and also it can be extended for forward flight.

C_T: Thrust coefficient

C_Q: Torque coefficient

R_T: Blade tip radius

U: Induced velocity in the axial direction

V_c: Vertical climbing flight

v_n: Induced velocity component perpendicular to W

W: Resultant velocity of fluid relative to blade

w: Induced velocity in the circumferential direction

C: Blade section chord

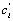: Lift curve slope of Blade section

y_c, y_i: Radial coordinate of control point where induced velocity is calculated

y_j: Radial location of chord-wise vortex in a blade segment

Greek Symbols

α: Geometric angle of attack

α_e: Effective angle of attack

α_i: Induced angle of attack

θ: Setting angle of attack

ϕ: Angle of the relative velocity of air at a blade section with respect to the plane of rotation

Γ: Circulation strength of vortex filament

η: Non-dimensional radial location (y/R_T)

Ω: Angular velocity of rotor

λ: Climb inflow ratio (Advance ratio)

Non-dimensional quantities