Forest Research: Open Access
Open Access

Allometric Equation for Aboveground Biomass Estimation for Selected Trees Shrubs in Gesha-Sayilem Moist Afromontane Forest

Author info »

Introduction

The estimation of above ground biomass in forest ecosystem is essential for assessing carbon sequestration potential of the forest for climate change mitigation and to determine volume of fuel wood harvest for assessing forest productivity [1,2] The reliable and accurate biomass estimates are important to implement mitigating policies and taking the advantage of the Reducing Emissions from Deforestation and Forest Degradation (REDD+), [3]. Under the United Nations Framework Convention on Climate Change (UNFCCC), countries have to report regularly the state of their forest resources through assessments of carbon stocks based on forest inventory data and allometric equations [2]. The allometric equation estimates the whole or partial mass of a tree from measurable tree dimensions, including trunk diameter, height, wood density, or their combination [4,5].

Allometric equations which are regression models that relate the biomass to some independent variables such as diameter, height and wood density that are easy to measure in the field and used to estimate tree components from the forest [6]. Allometric biomass equations have been developed for tree species in different ecological regions of the world, [7-9] the accuracy of AGB estimation using allometric models is highly dependent on the use of appropriate models [10]. The generic models can be developed for multiple species (general multispecies models) or for single species (general species-specific models). Species-specific models can result in accurate biomass estimates. As it is suggested by [8] use of multispecies AGB models is a more feasible solution for tropical forests, which are characterized by high species diversity. However, the generic equation developed by [9] may not adequately reveal the tree biomass in a specific region in tropics including in Ethiopia. Therefore, the use of species specific equations is important to achieve higher levels of accuracy because trees of different species may differ greatly in tree architecture and wood density.

Tropical forest is a major component of terrestrial carbon cycle and it has a great potential for carbon sequestration, accounting for 26% carbon pool in above ground biomass and soils [10]. However, in tropical forests, the accurate estimates of carbon sequestration are lacking due to a scarcity of appropriate allometeric models.

The Afromontane forest of Ethiopia covers more than 50% of the land area Yalden, NBSAP. The dry Afromontane forest is concentrated in central and northern Ethiopia and around churchyards. On the other hand, the Moist Evergreen Afromontane Forest (MAF) is widely distributed in south and southwestern Ethiopia. These forests have different tree and shrub species diversity and developing species specific allometric equations for biomass estimation is very important to estimate the carbon sequestering potential of moist Afromontane forest of south west Ethiopia. Thus, the aim of this study is to estimate aboveground and below biomass of the trees and shrubs of Gesha-Sayilem forest in order to develop species specific allometric equations of the forest.

Materials and Methods

Site description

The study area is located in the Southern Nations Nationalities Peoples Regional State (SNNPRS), in Kafa Zone at Gesha and Sayilem districts. It is located between 6°24’ to 7°70’ North and 35°69’ to 36°78’ East (Figure 1). The topography of the landscape is undulating, with valleys and rolling plateaus and some area with flat in the plateaus. The altitude ranges from 1,600 m to 3000 m [11]. The monthly mean maximum and minimum temperature for Gesha is 29.5°C and 9.5°C, respectively. On the other hand, the monthly maximum and minimum temperatures for Sayilem ranges 10°C to 25°C and the annual rainfall for both districts ranges 1853- 2004 mm.

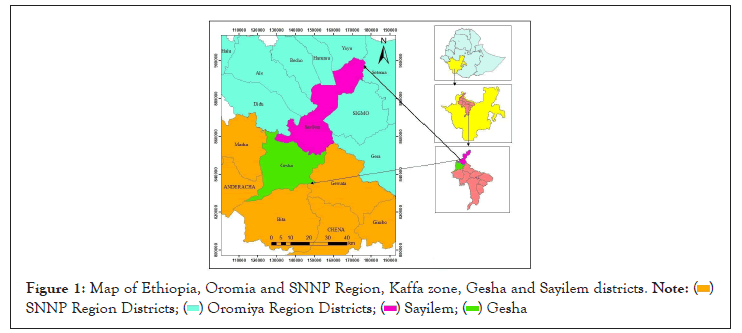
Figure 1: Map of Ethiopia, Oromia and SNNP Region, Kaffa zone, Gesha and Sayilem districts.

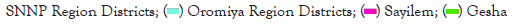
Target species description

The selected plants are characteristic species of, moist Afromontane forest which comprise Apodytes dimidata, Sapium ellipticum Ilex mitis, Gallinera saxifraga, and Vernonia aurcuiflera and they are the dominant in the area. Apodytes dimidata, is tree up to 25 m high with shining leaves growing in forest and open land. Ilex mitis is evergreen shrub, or more usually a tree 24- 40 m tall with attractive flower heads. Sapium ellipticum evergreen shrub or tree up to 25(-30) m high, branches drooping, buds protected by scales. Gallinera saxifrage is shrub grow up to 5 m high and found under the shade of forest layer. Similarly, Vernonia aurculifera are shrubs growing grow up to 4-5 m high or sometimes small tree up to 10 m tall, grow at forest margin and very attractive for honeybees.

Sampling methods

The procedures of semi-destructive methodology in tree volume building manual and biomass allometeric equations [12] were followed. [13] A random sampling method was used to select tree and shrubs in the study area in order to have an equal chance of being involved in the study. For sampling trees, individual plant species were categorized into woody plants who’s Diameter at Breast Height (DBH) is ≥ 5 cm. For sampling shrubs and sapling destructive sampling method was used following Lamprecht’s classification [14]. Based on the density and abundance of the species, a total of 150 individuals of five dominants plant species of Apodytes dimidiata, Ilex mitis, Sapium ellipticum and shrubs (Galiniera saxifraga and Vernonia auriculifera) were selected and 30 individuals from each trees and shrubs were used for the measurements. In order to represent the reasonable size of the diameter distribution and to minimize error of sampling, the trees were classified into five DBH classes and each class having six individuals per DBH class ranging from 10-20, 20.1-30, 30.1-40, 40.1-50, and greater than 50 cm were measured and recorded.

Field measurement

Non-destructive sampling method was used for the measurement of tree biomass, and the trees were divided into separate architectural elements (stem, branches and leaves). Serial measurements of the height and diameter of trunk were done at 2 m intervals by climbing on live trees using the ropes. For the determination of trimmed biomass, four branches whose circumference is less than 10 cm were trimmed down from the live tree using the machete [15]. The trimmed branches were separated into leaves and wood and the fresh weight of them were recorded (Figure 2).

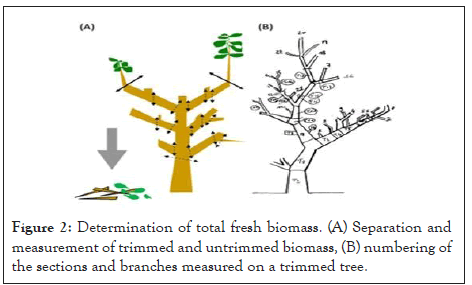
Figure 2: Determination of total fresh biomass. (A) Separation and measurement of trimmed and untrimmed biomass, (B) numbering of the sections and branches measured on a trimmed tree.

Laboratory measurement

A three replicates of 1 kg of sample of the wood and leave were weighed and placed in plastic bag, brought to the laboratory and oven dried at 105°C for 72 hours for wood, and 24 hours for leaves. The total dry weight of each AGB component was calculated using the ratio between the dry and fresh weight of the sub-samples, multiplied by the total fresh weight of the respective components. The basic wood density (gcm⁻³) of branches of the different sizes of the tree was estimated according to the water displacement method (Figure 3). The averaged WD (g/cm³) per sample tree was calculated as oven-dry weight divided by volume at saturation.

Figure 3: Measuring wood volume by water displacement Sampling of shrubs.

Sampling of shrubs

For determination of biomass shrubs (Galiniera saxifraga and Vernonia auriculifera), the shrubs were destructively sampled. The following parameters were measured such as stump diameter at 30 cm, DBH at 1.3 m, total height (h). The DBH of the shrubs ranged from 3.8-22.8 cm and 3.0 to 18.3 cm for Galiniera saxifraga and Vernonia auriculifera respectively. The fresh weight of each component was measured using a spring balance. To determine the dry matter content of the woods and leaves all branches from each stem were taken from thickest to the thinnest to make a composite sample and sealed in plastic bags and transported to laboratory. They were then oven- dried at 70°C for 24 hours and samples were weighed and the fresh to oven-dry weight ratios was calculated.

Estimation of aboveground biomass of tree

The above ground biomass of the tree was calculated by summing up of trimmed dry biomass and the untrimmed dry biomass of the sample trees.

Bdry=Btrimmed+Buntrimmed…................. (Equation 1)

Calculations of trimmed biomass

The trimmed biomass of sample tree was calculated from the fresh biomass Baliquot fresh wood of a wood aliquot and its dry biomass Bdrywoodaliquot, the moisture content was calculated as follow:

X wood=(Baliquot drywood)/(Baliquot freshwood)…. (Equation 2)

Where is moisture content of the wood, and where Baliquot dry wood, is the oven-dried wood biomass of the aliquot in the sample and where Baliquot fresh wood, is the fresh wood biomass of the branch aliquot in the sample. Similarly, the moisture content of the leaves was calculated from the fresh biomass B fresh leaf aliquot of the leaf aliquot and its dry biomass B dry leaf aliquot as follow:

X Leafi=(Baliquot dryleafi)/(Baliquot freshleafi)… (Equation 3)

Trimmed dry biomass was then determined as

Btrimmed dry=B trimmed fresh wood *X wood+ B trimmed fresh leaf *X leaf…… (Equation 4)

Where, B trimmed fresh leaf is the fresh biomass of the leaves stripped from the trimmed branches and Btrimmed fresh wood is the fresh biomass of the wood in the trimmed branches.

Calculating untrimmed biomass

Untrimmed biomass was calculated from two parts of the tree still standing (stem and large branches) and the other for small basal branches.

B untrimmed dry = B dry section+ B untrimmed dry branch …………………………………….. (Equation 5)

Each section i of the stem and the large branches were considered to be a cylinder of volume and volume of stem and large branches were calculated using Smalian’s formula.

Vi= π Li ((D² li+D² 2li) )/8…       (Equation 6)

Where Vi is the volume of the section i, its length, D21i and D22i are the diameters of the two extremities of section i. The dry biomass of the large branches and stem were being calculated from the product of mean wood density and total volume of the large branches and the stem.

B dry section= ῥ*ΣVi …………… (Equation 7)

Where ῥ the mean wood density was expressed in gcm⁻³, then volume Vi was expressed in cm³ and the mean wood density was calculated by:

ῥ=(Baliquot drywood)/(Valiquot fresh wood) ........… (Equation 8)

The dry biomass of the untrimmed small branches was then calculated using a model between dry biomass of trimmed branches and its basal diameter. This model is established by following the same procedure as for the development of an allometric model, using a simple linear regression model which is expressed as

Bdry branch=a+bD^c ….................................… (Equation 9)

Where a, b and c are model parameters and D branch basal diameter,

Estimation of below ground biomass (BGB)

The total aboveground biomass of a tree has been good predictors of its belowground biomass. Total root biomass for each of the study trees were calculated following [15-26]. Thus, a conversion factor of 0.24 for tropical rain forest was used to calculate the below ground biomasses of each of the study trees from their total aboveground biomass.

BGB=AGB x 0.24 ……………………… (Equation 10)

Data analysis and model selection

Relationships between basal diameters and dry weight of trimmed branches including twigs and leaves were computed using linear regression models. The assumptions of linear regression model were checked by observing the normal distribution of residuals on P-P plots. Because of the heteroscedasticity nature of biomass data, the data were transformed using a natural logarithm. Furthermore, Pearson correlation analysis was carried out between the response variable (Dry weight of the biomass) and the independent variables (DBH) to examine whether there was the linear relationship between dependent and independent variables (Table 2). In order to identify the multicollinearity with log-transformed models multi collinearity test was carried out using a variance factor [26]. A value greater than 10 variance inflation factor (VIF>10) is an indication of potential multicollinearity among independent variables. Then selection of the best fit model was based on the goodness fit statistics calculated for each species specific equation such as adjusted coefficient of determination (R² adj), standard error of the mean (SE) and Akaki Information Criterion (AIC).

Results

Above ground biomass

The summary of the mean, maximum and minimum DBH, height and wood density and dry weight of five plant species were summarized in Table1. The highest mean dry weight of the above ground biomass was obtained for Apodytes dimidiata, followed by Sapium ellipticum and Ilex mitis. Similarly, the highest mean above ground biomass shrubs were obtained for Galiniera saxifraga and least was obtained for Vernonia auriculifera. The analysis of the different sub biomass compartments of trees and shrubs indicated that the stem comprises the greater biomass as compared to branches and leaves accounting for 72%, 65.9% and 54.7% of the biomass stem in Apodytes dimidiata, Ilex mitis and Sapium ellipticum respectively (Table 1).

The person’s correlation analysis between above ground biomass and dendrometric variables (DBH, height and wood density) were shown in Table 2. The above ground biomass was strongly correlated with DBH and it is the most influential factors affecting the biomass of the trees and shrubs. Height is second important factor correlated strongly with biomass while wood density was poorly correlated with above ground biomass. Furthermore, the analysis of sub biomass compartment of trees and shrubs showed that stem biomass is strongly correlated with DBH in all studied species but wood density is poorly correlated except for Apodytes dimidiata and Sapium ellipticum and no significant correlation were obtained with height. Both branches and foliage’s were positively correlated with DBH and height but no significant correlation with wood density.

Table 2: Pearson’s correlation coefficients between biomass compartments (stem, branches and above ground biomass) and dendrometric variables (diameter, height, wood density) for tree and shrub species.

Trimmed twigs and leave biomass of the tree

The average trimmed wood aliquot moisture content from oven dry biomass varied from 0.34% in Sapium ellipticum to 0.54% in Apodytes dimidiata while the average leaf aliquot moisture content ranged from 0.32%, in Ilex mitis to 0.4% in Apodytes dimidiata (Table 3). The mean dry wood biomass was highest for Ilex mitis and followed by Sapium ellipticum and Galiniera saxifraga. The lowest dry wood biomass was obtained for Vernonia auriculifera. Similarly, the dry leaf biomass was higher for Ilex mitis and relatively lower for the rest of the species. The overall dry section of trimmed branch including twigs and leave biomass highest for Ilex mitis (5.5 kg) and followed by Apodytes dimidiata (4.2 kg) and Sapium ellipticum (3.4).

Table 3: Allometeric equations for determining Trimmed twigs and leaves of the trees.

Regression model for determination of biomass of the small branches

From the regression model between the dry biomass of trimmed biomass and the basal diameter, values of “a” and “b” were known and the biomass of untrimmed small branches which was on the tree were determined by inserting the basal diameter to the model equations “a+bD^c” (Table 4). Accordingly, the average biomass of untrimmed small branches for Ilex mitis, Apodytes dimidata and Sapium ellipticum were 46, 121 and 86 (kg) respectively.

Table 4: Allometric equations for determining untrimmed dry biomass of the small branches of the species.

Biomass distribution within trees compartments

The distribution of mean biomass fractions for the trees and shrubs showed that on average stem, branch and leaf biomass contributed 70.8%. 24.6% and 1.47% of above ground biomass in Apodytes dimidata (47.8%, 49.2% 2.9%) Sapium ellipticum (82.4, 34.7, 8.11%) in Ilex mitis (36.5%, 34.3% 29.17%), Gallinaria saxifraga) and 34.6%, 49.8%, 15.6% Vernonia auriculifera respectively in Figure 4. The highest percentage of stem biomass accumulated in Ilex mitis, Apodytes dimidata and Gallinaria saxifraga. The branch biomass was also highest in Sapium ellipticum and Vernonia auriculifera. Foliage had the lowest contribution towards the total biomass in all species.

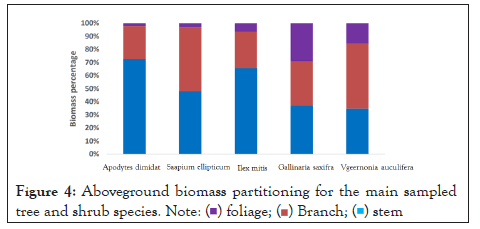
Figure 4: Aboveground biomass partitioning for the main sampled tree and shrub species.

Model selection and validation

The calculated model parameters for the above ground biomass were statistically significant (p<0.001) with independent variables and the adjusted R2 value ranges between 70-87% and lower value of AIC (Akaike information criterion) were obtained (Table 5). Accordingly, the combination of DBH, Height and wood density model provided the best fit in Apodytes dimidata with adj R² value of 0.87 and standard error percentage of 0.63. On the other hand, the DBH and height were found to be the best fit variables for Gallinaria saxifraga and Sapium ellipticum with R², value of 0.73 and 0.81 and AIC value of 34.24 and 59.25 respectively. The DBH alone provided the best fit in Ilex mitis and Vernonia auriculifera with adj R² the value of 0.87 and 0.70 and lower standard error and AIC and variance infilation factor was obtained.

Table 5: Model description for the fitted models of the above ground biomass for the study species.

Discussion

The biomass models for moist Afromontane forest species of the southwest Ethiopia are valuable tools for the estimation of carbon stocks to mitigation climate change. Different authors have attempted to generate biomass equations for tropical forests for the estimation of aboveground biomass and these equations may not accurately be revealed the tree biomass in a specific region due to variability in wood density and the architecture of trees among and within species. [16-18] However, little attention has been given to develop the species-specific biomass equation and it is available for tropical trees [19]. On view of this, biomass equations were developed for the above- ground biomass of the study species (Apodytes dimidiata, Ilex mitis, Sapium ellipticum, Galiniera saxifraga and Vernonia auriculifera). A goodness of fit, statistics using multiple regression model showed that combination of DBH, height and wood density were provided best fit for Apodytes dimidata while DBH and height provided the best fit for Galiniera saxifraga and Sapium ellipticum. On other hand only DBH showed the best fit for Ilex mitis, and Vernonia auriculifera (Table 5). The inclusion of the wood density provided best fit for Apodytes dimidata, which increased the aboveground biomass prediction significantly with an adjusted R² of values of 0.73 and an average standard deviation of 16.9% and 18.2% respectively. This is in agreement with [8,20] observed that the equation including wood density improved biomass in moist forest of tropical Africa and Asia. In addition to this, the most important predictor of above ground biomass is usually DBH [21]. A measurement of height, wood density and the higher diameter can also be included if they significantly reduce the volume prediction error [22-23] also indicated in the Amazonian watershed, the inclusion of wood density and height revealed spatial biomass and carbon patterns of the forest. Thus, introducing wood density as a biomass predictor may explain the site variations, species variations and increase precision of the estimations. The addition of the height in the biomass model also affected the biomass estimation for Sapium ellipticum and Galiniera Saxifraga. The height of the trees could include information about competition or fertility of the site and may yield less-biased estimates. Though accurate measurement of total height may be challenging in the field. According to [8] observed a standard error reduction across all tropical forests types from 19.5% when total height was not included to 12.5% when total height was available. Allometric equations that don’t utilize tree height can over predict large diameter tree biomass [24].

The variation in aboveground biomass was also explained by DBH for Ilex mitis and Vernonia auriculifera. Since DBH is the best predictor variable for above ground biomass in allometric models because it is strongly correlated with biomass and it can be easily measured in the field and is always available in forest inventories data [7,25].

The high proportion of biomass was accumulated in the stem and big branches of Apodytes dimidata, Ilex mitis and Sapium ellipticum. The branch biomass of Ilex mitis is largest as compared to others due to spreading canopy that holds more branches and leaves and also it might be protected from external disturbances. This is in agreement with [12,26] reported that herbivores and inter-plant competition can affect the branch biomass and its geometry. [27-32] the smaller biomass was accumulated in small branches and leaves. This is due to the fact that dense forests with strong competition for light and space, the trees tend to develop smaller branches and foliage which resulted for the lower biomass. This study [33-38] is in agreement with found percentage stem biomass is found to higher than for branch and leaf.

Conclusion and Recommendation

Developing an allometric equation is an important method for the assessment of tree biomass. It has also an indirect contribution for monitoring of the global carbon cycle. Adopting the generic allometeric equation for the specific forest stand has limitation due to ecological variation and diversity of trees and shrubs. Species- specific allometric equations were formulated for five tropical species (Apodytes dimidata, Sapium ellipticum Ilex mitis, Gallinera saxifraga, and Vernonia aurcuiflera) following the semi destructive sampling procedure. The formulated equations are proposed as a species-specific equation particularly in the Afromontane rainforest as well as in the montane moist forest ecosystem of southwestern Ethiopia. Thus the study indicated that combination of DBH, height and wood density model provided the best fit in Apodytes dimidata while the DBH and height were found to be the best fit model for Gallinaria saxifraga and Sapium ellipticum. On the other hand, the DBH alone provided the best fit in Ilex mitis and Vernonia auriculifera. Therefore, the specific allometeric equation model developed in this study can be used for estimating forest carbon stocks, identifying carbon sequestration capacity of trees and shrubs. As Ethiopia has many tree species, it is recommended to develop species-specific allometric equations for all of them for better assessment of carbon stock to meet national and international reporting requirements for greenhouse gas inventories.

Acknowledgements

The authors are thankful to the Addis Ababa University and Oromia Agricultural Research Institute for providing the required facilities and logistics. Our sincere thanks also to Holeta Agriculture Research center for helping us in the laboratory.

Author's Contributions

All authors have contribution. Admassu Addi perceived the research; contributed to data analysis and wrote the draft manuscript; TS and TB, edited and improved the manuscript and prepared for the publication. All authors read and approved the final manuscript.

Funding

This research was supported by Oromia Agricultural Research Institute Government fund.

Availabilty of Data and Materials

The datasets used and/or analyzed during the current study are available from the corresponding author when requested.

Ethics Approval and Consent to Participate

Not applicable.

Consent for Publication

Authors give full permission for the publication, reproduction, and broadcast.

Competing Interests

The authors declare no conflict of interest.

References

1. Makungwa SD, Chittock A, Skole DL, Kanyama-Phiri GY, Woodhouse IH. Allometry for biomass estimation in Jatropha trees planted as boundary hedge in farmers’ fields. Forests. 2013;4:218-233.

   [Crossref] [Google Scholar]

2. Preece ND, Crowley GM, Lawes MJ, van Oosterzee P. Comparing above ground biomass among forest types in wet tropics: Small stems and plantation types matter in carbon accounting. For Ecol Manage. 2012;264:228-237.

   [Crossref] [Google Scholar]

3. Kangas A, Maltamo M. Forest inventory. Methodology and Applications. Managing Forest Ecosystems. Springer, Dordrecht, the Netherlands. 2006.

   [Google Scholar]

4. Kuyah S, Dietz J, Muthuri C, Jamnadass R, Mwangi P, Coe R, et al. Allometric equations for estimating biomass in agricultural landscapes: I. Aboveground biomass. Agric Ecosyst Environ. 2012;158:216-224.

   [Crossref] [Google Scholar]

5. Adrien N, Djomo C, Chimi D. Tree allometric equations for estimation of above, below and total biomass in a tropical moist forest: Case study with application to remote sensing. For Ecol Manage. 2017;391:184-193.

   [Crossref] [Google Scholar]

6. Rebeiro CS, Fehrmann L, Boechat Soares CP, Gonçalves Jacovine LA, Kleinn C, de Oliveira Picard N, et al. Manual for building tree volume and biomass allometric equations: from field measurements to prediction. Rome: Food and Agricultural Organization of the United Nations. 2012.

   [Google Scholar]

7. Chave J, Andalo C, Brown S, Cairns MA, Chambers JQ, Eamus D, et al. Tree allometry and improved estimation of carbon stocks and balance in tropical Forests. Oecologia. 2005;145:87-99.

   [Crossref] [Google Scholar]

8. Chave J, Réjou-Méchain M, Búrquez A, Chidumayo E, Colgan MS, Delitti WB, et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob Chang Biol. 2014;20:3177-3190.

   [Crossref] [Google Scholar]

9. Grace J. Understanding and Managing the Global Carbon Cycle. J Ecol. 2004;92:189-202.

   [Crossref] [Google Scholar]

10. Dieler J, Pretzsch H. Morphological plasticity of European beech (Fagus sylvatica L.) in pure and mixed-species stands. For Ecol Manage. 2013;295:97-108.

    [Crossref] [Google Scholar]

11. Addi A, Demissew S, Soromessa T, Asfaw Z. Carbon Stock of the Moist Afromontane Forest in Gesha and Sayilem Districts in Kaffa Zone: An Implication for Climate Change Mitigation. J Ecosyst Ecography. 2019;9(1):1-8.

    [Google Scholar]

12. Djomo  A,  Ibrahima  A,  Saborowski  J, Gravenhorst G. Allometric Equations for Biomass Estimations in Cameroon and Pan Moist Tropical Equations Including Biomass Data from Africa. For Ecol Manage. 2010;260(10):1873-1885.

    [Crossref] [Google Scholar]

13. Lamrecht H. Silviculture in the tropics. Tropical forest ecosystems and their tree species Possibilities and methods in the long-term utilization. Germany. 1989.

    [Google Scholar]

14. MacDicken K. A Guide to Monitoring Carbon Storage in Forestry and Agroforestry Projects. Forest Carbon Monitoring Program. Winrock International, Arlington, VA, USA. 1997.

    [Google Scholar]

15. Pilli R, Anfodillo T, Carrer M. Towards a functional and simplified allometry for estimating forest biomass. For Ecol Manage. 2006;237:583-593.

    [Crossref] [Google Scholar]

16. Tadese S, Soromessa T, Bekele T, Bereta A, Temesgen F. Above Ground Biomass Estimation Methods and Challenges: A Review. Journal of Energy Technologies and Policy. 2019;9(8):12-25.

    [Crossref] [Google Scholar]

17. Ancelm MW, Edward ME, Luoga E, Ernest MR, Zahabu E, Santos SD, et al. Allometric Models for Estimating Tree Volume and Aboveground Biomass in Lowland Forests of Tanzania. International Journal of Forestry Research. 2016;1-13.

    [Crossref] [Google Scholar]

18. Edae DD, Soromessa T. The  accuracy  of  species‑specific  allometric  equations  for estimating aboveground biomass in tropical moist montane forests: case study of Albizia grandibracteata and Trichilia dregeana. Carbon Balance Manage. 2019;14(18):1-13.

    [Crossref] [Google Scholar]

19. Brown S, Gillespie AJR, Lugo AE. Biomass estimation methods for tropical forests with applications to forest inventory data. For Sci. 1989;35(4):881-902.

    [Crossref] [Google Scholar]

20. Nogueira SL, Soares BG, Ribeiro N, Sitoe A. Biomass allometric equation and expansion factor for a mountain moist evergreen forest in Mozambique. Carbon Balance Manag. 2018;13(23):1-16.

    [Crossref] [Google Scholar]

21. Köhl M, Magnussen SS, Marchetti M. Sampling methods, remote sensing and GIS multi- resource forest inventory. New York: Springer. 2006.

    [Crossref] [Google Scholar]

22. Alvarez E, Duque A, Saldarriaga J, Cabrera K, Del Valle G, Lema A, et al. Tree above-ground biomass allometries for carbon stocks estimation in the natural forests of Colombia. Forest EcolManage. 2012;267:297-308.

    [Crossref] [Google Scholar]

23. Heath LS, Hansen MH, Smith JE, Smith WB, Miles PD. Investigation into CalculatingTree Biomass and Carbon in the FIADB Using a Biomass Expansion Factor Approach. In: McWilliams W, Moisen G, Czaplewski R, editors. 2008.

    [Google Scholar]

24. Zianis D, Mencuccini M. On Simplifying Allometric Analyses of Forest Biomass. Forest Ecology and Management. 2003;187:311-332.

    [Crossref] [Google Scholar]

25. Mehari A, Andr´es B, Bravo.Fe. Ricardo Ru. Aboveground biomass equations for sustainable production of fuelwood in a native dry tropical afro-montane forest of Ethiopia. 2016;3(2):411-423.

    [Crossref] [Google Scholar]

26. Henry M, Besnard A, Asante WA, Eshun J, Adu-Bredu S, Valentini R, et al. Wood density, phytomass variations within and among trees, and allometric equations in a tropical rainforest of Africa. For Ecol Manage. 2010;260:1375-1388.

    [Crossref] [Google Scholar]

27. David RV, Peter AP, Richard G S. Allometric equations for two South American Conifers: Test of non-destructive method. For Ecol Manage. 1997;106:55-71.

    [Crossref] [Google Scholar]

28. Brown S. Measuring carbon in forests: Current status and future challenges. Environmental Pollution. 2012;116:363-372.

    [Crossref] [Google Scholar]

29. Brown S, Lugo A.E. Above-ground biomass estimates for tropical moist forests of the Brazilian Amazon. Interciencia. 1992;17:8-18.

    [Google Scholar]

30. Brown S. Estimating biomass and biomass change of tropical forests: A Primer. FAO Forest Paper, FAO, Rome; P.134. 1997.

    [Google Scholar]

31. Addi A, Soromessa T, Bareke T. Plant diversity and community analysis of Gesha and Sayilem Forest in Kaffa Zone, southwestern Ethiopia. Biodiversitas. 2020;21(7):2878-2888.

    [Crossref] [Google Scholar]

32. Gaspar R. Above- and belowground biomass in a Brazilian Cerrado. For Ecol Manage. 2011;262:491-499.

    [Crossref] [Google Scholar]

33. Henry M, Picard N, Trotta C, Manlay RJ, Valentini R, Bernoux M, et al. Estimating tree biomass of sub-Saharan African forests: a review of available allometric equations. Silva Fenn. 2011;477-569.

    [Google Scholar]

34. R Core Team. R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing. 2016. http://www.R-project.org/.

    [Google Scholar]

35. Tekele D. Allometric equation for biomass estimation of Allophyllus abyssinicus and Croton macrostachyus in Arba Gugu forest, Arsi Zone Oromia Region, Ethiopia. MSc Thesis, Addis Ababa University, Ethiopia. 2014.

    [Google Scholar]

36. Worku E, Soromessa T. Allometric Equation for Biomass Determination in Juniperus procera and Podocarpus falcatus of Wof-Washa Forest: Implication for Climate Change Mitigation. American Journal of Life Sciences. 2015;3(3):190-202.
37. Vahedi AA, Matajil A, Babayi-Kafakil S, Eshaghi-Rad J, Hodjati SM, Dojmo A. Allometric equations for predicting above ground biomass of beech-horn beam stands in the Hycanian forests of Iran. Journal of forest Science. 2014;60:236-247.

    [Crossref]  [Google Scholar]

38. Vorster AG, Evangelista PH, Stovall AL, Seth Ex. Variability and uncertainty in forest biomass estimates from the tree to landscape scale: the role of allometric equations. Carbon Balance Manage. 2020;15(8):1-20.

    [Crossref] [Google Scholar]