Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2015) Volume 8, Issue 1
Background: Alternative splicing of messenger RNAs provides cells with the opportunity to create protein isoforms of a multitude of functions from a single gene by excluding or including exons during post-transcriptional processing. Reconstructing the contribution of these splice variants on the total amount of gene expression remains difficult.
Methods: We introduced a probabilistic formulation of the alternative splicing reconstruction problem using a finite mixture model, and provide a solution based on the maximum likelihood principle. Our model is based on the assumption that the expected expression level of exons in a particular splice variant is the same for all exons in that variant but allows for measurement error. In this algorithm the expression in a patient can be written as a weighted sum of the number of splice variant mixture multivariate Gaussian densities. We estimated the model parameter by maximizing the total likelihood using a Nelder and Mead optimization algorithm in R. To evaluate our algorithm we compared the AIC/BIC values of six models: Established optimal normal mixture modeling method, all exons are equally transcripted, the currently known splice variants, all possible splice variants, the known variants aided with the high prevalent variants of the all possible variants model, and manually selected splice variants.
Results: We applied the models to three genes (SLC2A10, TGFβR2 and FBN1), with 25, 29 and 265 possible splice variants, associated with Marfan’s syndrome in gene/exon expression data of 63 patients with Marfan’s syndrome. The models with the known splice variants aided with the high prevalent splice variants from the all possible splice variants had the best AI C/BI C values for all three genes. In SLC2A10 and FBN1 there was one, in TGFβR2 two predominant splice variants.
Conclusion: We found four possible new splice variants in three genes associ- ated with Marfan’s syndrome.
Keywords: Alternative splicing, Marfan syndrome, Gene expression
Alternative splicing of messenger RNAs (mRNAs) provides cells with the opportunity to create a multitude of protein isoforms from a single gene by excluding or including exons during post-transcriptional processing [1-4]. Among multi-exon genes in the human genome, it is estimated that as many as 74% are alternatively spliced [3] and 15-50% of human disease mutations affect splice site selection [5].
There are five basic modes of alternative splicing (depicted in Figure 1), of which exon skipping is most common in humans [6]. Predicting the contribution of these modes of splicing variation on gene expression data is difficult, especially in microarray data which returns highly fragmentary information from probes targeting specific exons or exon-exon junctions [3,7,8]. In reconstructing splice variants, formulating a splice graph traversal problem can be helpful [9-11], especially when considering multiple traversals.
In reconstructing alternative splice variants all possible traversals can be considered [9,12], where in our situation the splice variants correspond to the different traversals. For larger genes this method potentially generates a very large number of random exon combinations, a gene with 65 exons for instance would result in 265 (3.69e19) possible splice variants. Another method is to use specific rules to produce a minimal set of splice variants to sufficiently explain the variation in the input data [10,13,14]. Some researchers have suggested using established Multivariate Normal mixture/cluster analysis methods, without the biological information of splice variants, but this does not necessary result in a mixture of splice variants. In this manuscript, we introduce therefore a probabilistic formulation of the alternative splicing reconstruction problem using a finite mixture model, and provide a solution based on the maximum likelihood principle.
Model
We developed a finite mixture model to predict alternative splice variants within one gene. Our model is based on the assumption that the expected expression level of exons in a particular splice variant is the same for all exons present in the variant but we allow for differential measurement error.
The expression y in patient i is based on vector yi=(yi1 , . . . , yiE) with size E, the number of exons in the gene of interest.
The finite mixture model can be written as a weighted sum of the number of splice variants, K, of mixture multivariate Gaussian densities as given by 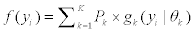 where
where 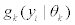 is a multi-variate probability distribution given parameters θk. Pk is the probability of the presence of the kth splice variant. These mixture weights satisfy the constraint that 0
is a multi-variate probability distribution given parameters θk. Pk is the probability of the presence of the kth splice variant. These mixture weights satisfy the constraint that 0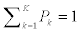 . The kth splice variant can be described by the vector
. The kth splice variant can be described by the vector 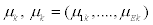 with Zjk=1 or 0 depending on if exon j is included, or excluded, from splice variant k.
with Zjk=1 or 0 depending on if exon j is included, or excluded, from splice variant k.
In our model each component density, 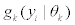 , is a multi-variate normal distribution function of the form
, is a multi-variate normal distribution function of the form
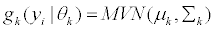 (1)
(1)
with mean vector, 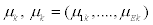 and covariance matrix Σk. When splice variant k is present, the mean expression of exon j, μjk, is assumed to be identical for of all exons included in splice variant k. We also assume that the expression of an exon included in a splice variant is the same when the exon is included in other splice variants. The mean expression of one exon is thus equal to the expression of all exons present in a splice variant, μjk=μ1. All exons excluded from splice variant k are not transcribed and should have an expression of zero. However, in microarray data there is always background noise. Therefore the expected expression of exons not present in splice variant k is μ0. We make similar assumtions for the variances and covariances of yi.
and covariance matrix Σk. When splice variant k is present, the mean expression of exon j, μjk, is assumed to be identical for of all exons included in splice variant k. We also assume that the expression of an exon included in a splice variant is the same when the exon is included in other splice variants. The mean expression of one exon is thus equal to the expression of all exons present in a splice variant, μjk=μ1. All exons excluded from splice variant k are not transcribed and should have an expression of zero. However, in microarray data there is always background noise. Therefore the expected expression of exons not present in splice variant k is μ0. We make similar assumtions for the variances and covariances of yi.
Mean vector μjk, the diagonal elements of Σjk, 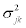 , with the covariances,
, with the covariances, 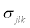 are specified by
are specified by
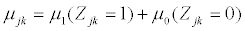 (2)
(2)
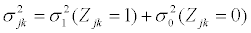 (3)
(3)
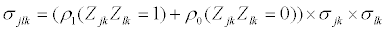 (4)
(4)
With the constraints; −1<ρ<1 and σ2>0. In our algorithm we estimated the Fisher z-transform of ρ and log (σ2).
We estimated parameter vector 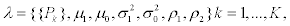 with (K - 1) + 6 parameters, by maximizing the total likelihood using a Nelder and Mead [15] optimization algorithm in R (version 3.0.2) with five sets of different stating parameters:
with (K - 1) + 6 parameters, by maximizing the total likelihood using a Nelder and Mead [15] optimization algorithm in R (version 3.0.2) with five sets of different stating parameters:
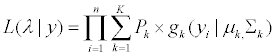 (5)
(5)
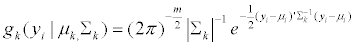 (6)
(6)
Model extension
As dedicated cells may be more expert in creating particular splice variants, and less equipped in producing other splice variants, the observed expression values do not only depend on probability of transcription of the splice variant, but also on the expression of each splice variant. In this case the mean, variance and correlation may depend on splice variant 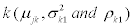 . We assumed the role of background noise the same in all splice variants. In this model the parameter vector to be estimated is
. We assumed the role of background noise the same in all splice variants. In this model the parameter vector to be estimated is 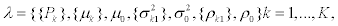 with 3K+(K-1)+3 parameters.
with 3K+(K-1)+3 parameters.
Analysis
To compare different mixture models we calculated the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) approximation, which adds a penalty to the log-likelihood based on the number of parameters. The AIC and BIC are defined as:
AIC=−2 * log(L) + 2 * number of parameters (7)
BI C=−2 * log(L) + number of parameters * log(n) (8)
We considered six models::
1. Established optimal normal mixture modeling method estimated by Mclust in R [16,17]; This is our null model, and positive control, because it has no constraints. Mclust has the disadvantage that it estimates clusters which almost surely are not corresponding to recognizable splice variants. The Mclust algorithm does not use constraints to simulate the biological process of alternative splicing. Mclust maximizes the likelihood using different parameter values for each exon in each splicing variant. Differences in expression values of several exons in one splicing variant are highly unlikely. The amount of mRNA transcribed in a splicing variant should be equal for all transcribed exons. However we expect that this model is usually the best model when AIC and BIC are concerned.
2. Only one splice variant is transcribed, namely the RNA molecule in which all exons are always all present. With respect to AIC and BIC we expect that this model is usually the worst. Therefore this model is our negative control and is also considered a null model.
3. Only known splice variants are transcribed. The known splice variants are based on the splice variants presented in the Ensembl genome database project [18] of June 2014. These splice variants are modeled in:
(a) The basic model with a mean expression equal in all splice variants and all exons.
(b) The extended model with a varying mean expression between splice variants.
4. All possible splice variants are transcribed. This results in a set of 2E number of splice variants representing all possible variants within the gene. This set of splice variants is modeled in:
(a) The basic model with a mean expression equal in all splice variants and all exons.
(b) The extended model with a varying mean expression between splice variants.
For genes with less than 10 exons we estimate the model with all possible splice variants. For 10 exons this would result in 1024 splice variants. For big genes the set of splice variants is too large. We therefore used a scenario-based method to estimate the parameters in this model. Each scenario consisted of a set of splice variants with similar exon skipping patterns, and had a fixed number of connected exons not present in each splice variant. The number of connected exons differs between scenarios. In the first scenario all splice variants with all exons present and skipping 1 exon are included.

The second scenario included skipping two connecting exons.

The last two scenarios consisted of only two or even one exon present and all other exons absent. This resulted in sets of three and two splice variants for the last two scenarios
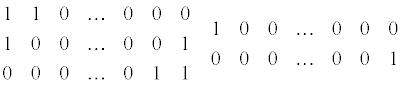
These multiple scenario’s each estimated a set of different splice variants de- pending on the size of the gene.
5. Here we combined the known splice variants (model 3) with the splice variants that have a mixture proportions in model 4. For genes with more than 10 exons we combine the known splice variants with the highest mixtures proportions of all scenario’s in a set of splice variants identical to genes <10 exons. We expect that this model is better than model 3 and 4 with respect to AIC and BI C.
6. We manually selected a number of splice variants based on the observed pattern of exon expressions in patients.
Simulation
The primary objective of the simulation study was to validate our model and algorithms. The simulation was conducted using predefined splice variants and model parameters. We simulated variation of a set of two known splice variants for each of three genes existing of 5, 9 and 65 exons, and added one unknown variant.
We estimated the parameters for the models with known splice variants (model 3a), all splice variants (model 4a), known splice variants added with the splice variants with the highest proportion in the model with all splice variants (model 5) and we used the manual model (model 6) with the simulated splice variants and their prevalences. For the simulation of the gene having 65 exons we did not estimate the all possible splice variants model and compared solely the known variants model to the model with the known splice variants with addition of the unknown splice variant, given that this would be the variant with the highest prevalence in the scenario’s of model 4a. We evaluated the models on their ability to reproduce the given parameters and compared the AIC and BI C. Additionally, to evaluate the models ability to identify the simulated splice variants, we calculated the fraction of times the simulated splice variant was identified using the various models we studied. To validate our model we have conducted a 7-fold cross-validation study on the simulation data of the gene with 5 exons. We selected the model with the lowest residual sum of squares (RSS) values as final model.
As secondary objective we tried to find the limit of the number of splice variants our model could estimate at once.
Data example
Our model was applied to microarray gene expression data of 63 patients with Marfan’s syndrome derived from a skin biopt [19]. The gene expression was obtained from a skin biopt taken from the upper thigh or upper arm with a 4.0 mm diameter punch. Gene expression was analyzed using Human Exon 1.0 ST Arrays and Affymetrix. The average RNA yield was 1.5 μg with an average RNA quality RIN value of 8.1. To generate the average log2 probe signal for the Affymetrix GeneChips, raw probe intensities without control probes were used.
We applied the mixture model to three genes, SLC2A10, TGFβR2 and FBN1, all associated with Marfan’s syndrome.
SLC2A10 consists of 26.86 kb pairs in five exons located at 20q13.12. Currently, there are two splice variants known (on October 2014 [18], [1 1 1 1 1] and [1 1 0 0 0]) of the total set of 32 possible splice variants, where 1 resembles the exon present an 0 the exon not present in the splice variant.
TGβR2 consists of 87.64 kb in 9 exons located at 3p22 with two known splice variants ([1 1 1 1 1 0 1 1 1] and [1 0 1 1 1 0 1 1 1]) of the 512 possible splicing variations of TGFβR2.
FBN1 is the largest gene (237.54 kb in 65 exons at 15q21.1) we analyzed and had 8 known splice variants of the 3.69e19 possible splice variants.
Simulation
The results from the simulation of the gene with 5 exons is presented in Table 1. Here the AI C and BI C values of models 5 and 6 are best. The mean values of the parameters and the probabilities were unbiased in both models where we used existing splice variants (model 5 and 6). These results were very similar for the genes having 9 and 65 exons. In the model estimating all possible splice variants the prevalences of the splice variants were lower than the simulated values. In this model the number of parameters is much larger than the number of observations making estimated rather unstable.
| Simulated data | Model 3a | CV 3 | Model 4a | CV 4 | Model 5 | CV 5 | Model 6 | CV 6 | |
|---|---|---|---|---|---|---|---|---|---|
| # of SV | 3 | 2 | 3 | 32 | 32 | 3 | 3 | 3 | 3 |
| log L | -720.31 | -882.16 | -570.07 | -567.24 | |||||
| # params | 7 | 37 | 8 | 8 | |||||
| AIC | 1454.61 | 1150.47 | |||||||
| BIC | 1477.7 | 1176.86 | |||||||
| RSS | 815.75 | 1396.51 | 932.92 | 796.93 | |||||
| µ1 | 9.5 | 9.5 | 9.5 | 9.52 | 9.53 | 9.47 | 9.52 | 9.5 | 9.5 |
| µ0 | 6 | 7.82 | 7.83 | 8.71 | 6.01 | 6.08 | 6.31 | 6.08 | 6.09 |
| σ2 | 0.15 | 0.16 | 0.16 | 0.24 | 0.31 | 0.15 | 0.15 | 0.16 | 0.16 |
| σ2 | 0.25 | 3.1 | 2.90 | 2.13 | 0.24 | 0.18 | 0.28 | 0.18 | 0.19 |
| ρ1 | 0.2 | 0.27 | 0.25 | 0.85 | 0.63 | 0.25 | 0.24 | 0.25 | 0.25 |
| ρ0 | 0 | 0.27 | 0.20 | 0.47 | 0.27 | 0.15 | 0.3 | 0.05 | 0.04 |
| 1 1 1 1 1 | 0.85 | 0.843 | 0.836 | 0.11 | 0.28 | 0.842 | 0.75 | 0.85 | 0.85 |
| 1 0 0 0 0 | 0.05 | 0.157 | 0.164 | 0.027 | 0.015 | 0.044 | 0.19 | 0.05 | 0.05 |
| 1 1 1 1 0 | 0.1 | 0.091 | 0.066 | 0.114 | 0.059 | 0.1 | 0.1 |
# of SV=Number of splicing variants; log L= log likelihood;
# of params=Number of parameters; AIC =Akaike information criterion; BIC=Bayesian information criterion; RSS=Residual Sum of Squares
Model 3a=Known splice variants; Model 4a=All possible splice variants; Model 5=Known and high mixture proportions splice variants; Model 6=Manually selected splice variants CV= Cross-validation analysis of corresponding model
Table 1: Results on the simulation data of 5 exons and three splicing variants.
However the splice variants with the highest prevalence in the simulated data always had the highest estimates, so the splice variants were in the correct order. When only the most frequent splice variants were used, the estimates were similar to the simulated values.
In Table 2 we show the fraction of times the simulated splice variant was identified using the various models we studied. Model 6 was the mixture model that was based on evaluating the available data. As may be expected, the performance of this model was perfect; all three variants were always identified. In practice where we do not know the true splicing variants, this model’s performance will be less good and we expect that splicing variant identified by an arbitrary observer will be often difficult to validate. With the models using algorithmic methods to identify variants (models 3-5), performance is less good. If we exclude unknown variants, identification of existing (i.e. known and high prevalent) variants is usually very good (model 3, variant 1). Performance of the biggest model (model 4), evaluating all possible variants, is clearly worse, also for the most prevalent variant. The performance of the more restricted model 5 seemed to be quite good for high prevalent variants (variant 1) and quite acceptable for low prevalent variants (variants 2/3).
| Variant | 1 | 2 | 3 |
|---|---|---|---|
| Model 3 | 98.4% | 30.5% | - |
| Model 4 | 32.9% | 30% | 66% |
| Model 5 | 88.2% | 26.3% | 59% |
| Model 6 | 100% | 100% | 100% |
Model 3=Known splice variants; Model 4=All possible splice variants; Model 5=Known and high mixture proportions splice variants; Model 6=Manually selected splice variants
Variant 1=[1 1 1 1 1]
variant 2=[1 0 0 0 0]
variant 3=[1 1 1 1 0]
Table 2: Percentage of correctlt identified splice variants.
The 7-fold cross-validation study showed similar results as our model.
Data example
SLC2A10: Because SLC2A10 consists of five exons with 25 possible traversals, we analyzed all 32 traversals as mentioned in model 4a. We estimated model 1, 2, 3a, 4a, 5 and 6. In addition we estimated the parameters for the model where we allowed for a varying mean between splice variants (models 3b and 4b). For model 6 we selected three splice variants ([1 1 1 1 0], [1 1 1 1 1], and [1 0 0 0 0]), which we expected could explain the variation in exon expression between patients. We assumed that these splice variants were equally present.
The results of the different models for SLC2A10 exon expression are reported in Table 3.
| Model 1 | Model 2 | Model 3a | Model 3b | Model 4a | Model 4b | Model 5 | Model 6 | |
|---|---|---|---|---|---|---|---|---|
| # of SV | 1 | 1 | 2 | 2 | 32 | 32 | 7 | 3 |
| log L | 39 | -546 | -496 | -546 | -478 | -377 | -388 | -413 |
| # params | 20 | 3 | 7 | 12 | 37 | 192 | 12 | 8 |
| AIC | -39 | 1098 | 1005 | 1116 | 1030 | 1139 | 800 | 841 |
| BIC | 4 | 1105 | 1020 | 1142 | 1110 | 1550 | 826 | 858 |
# of SV=Number of splicing variants; log L= log likelihood;
# of params=Number of parameters; AIC=Akaike information criterion; BIC=Bayesian information criterion.
Model 1=Mclust model; Model 2=One splice variant; Model 3=Known splice variants; Model 4=All possible splice variants; Model 5=Known and high mixture proportions splice variants; Model 6=Manually selected splice variants the a. and b. define the normal model or the extended model respectively
Table 3: SLC2A10 model results.
The optimal hierarchical clustering model (model 1) was found to be a model with only one cluster. The average exon expression is illustrated by the black line in Figure 2. This line closely followed the trend observed in all patients, but it did not reflect a recognizable splice variants. If we assumed that this gene had only one splice variant (with the same mean for all exons; model 2) we observed AIC/BI C values of 1098/1105.
If we assumed that only the known splice variants were present (models 3a and 3b), the AIC /BI C improved considerably to 1005/1020 or 1116/1142 depending on whether we allowed the mean expression to vary over splice variants (model 3b) or not (model 3a).
These results did not improve if we considered all possible splice variants (models 4a and 4b). However, in these models we observed that there were 5 variants ([0 1 1 1 1], [1 0 1 1 1], [1 1 0 1 1], [1 1 1 1 0] and [1 0 1 1 0]) present with a prevalence >0.05 varying between 0.07 and 0.13 which were not the known variants. Therefore, we finally tried the model with the two known variants together with the newly found variants (model 5). This model did had the best AIC/BI C values (800/826) of all models based on splice graphs traversals, and followed the trend closely as presented in Figure 2.
TGFβR2: TGβR2 consists of 9 exons with 29 (512) possible traversals and three known splice variants. The analyzed models were identical to the SLC2A10 gene. Except for the model 4b and the model where we predetermined the splice variants (model 6). Here we selected four splice variants ([1 0 1 1 1 1 1 1 0], [1 1 1 0 0 0 0 0 0], [0 1 1 0 0 0 0 0 0], [0 1 1 0 0 0 1 0 0]) with the prevalence of 20% 20% 40% 20%, respectively.
All results of the models for the exon expression of TGFβR2 are presented in Table 4.
| Model 1 | Model 2 | Model 3a | Model 3b | Model 4a | Model 5 | Model 6 | |
|---|---|---|---|---|---|---|---|
| # of SV | 1 | 1 | 2 | 2 | 512 | 4 | 4 |
| log L | 160 | -691 | -643 | -618 | -630 | -397 | -495 |
| # params | 54 | 3 | 7 | 12 | 517 | 9 | 9 |
| AIC | -211 | 1387 | 1301 | 1260 | 2295 | 811 | 1007 |
| BIC | 96 | 1394 | 1316 | 1286 | 3403 | 830 | 1026 |
# of SV=Number of splicing variants; log L=log likelihood;# of params=Number of parameters; AIC=Akaike information criterion; BIC=Bayesian information criterion. Model 1=Mclust model; Model 2=One splice variant; Model 3=Known splice variants; Model 4=All possible splice variants; Model 5=Known and high mixture proportions splice variants; Model 6=Manually selected splice variants the .a and .b define the normal model or the extended model respectively.
Table 4: SLC2A10 model results.
Similar to SLC2A10 the hierarchical cluster analysis, model 1, found one cluster. When we assumed that there was only one splice variant present in this gene (model 2) we found AIC/BI C values of 1387/1394.
The AIC/BI C improved to 1301/11316 or 1260/1286, if we assumed that only the known splice variants were present (model 3a and 3b), depending on whether we allowed the mean expression to vary over splice variants (model 3b) or not (model 3a).
AIC/BI C did not improve if we considered all possible splice variants for this gene. In these models two splice variant of the form [0 1 1 1 0 0 0 0 0] and [0 1 1 0 0 0 0 0 0] were present with a large prevalence. When we tried to improve the results of models 3a and 3b by adding these splice variants to the known splice variants (model 5) we found that this model had the best values for AIC/BI C (811/830).
FBN1: FBN1 is the largest gene we analyzed and has 8 known splice variants within 65 exons.
We applied our model to the 8 known splice variants of FBN1 (model 3a). Because all possible splice variants of FBN1 would generate 265=3.69e + 19 variants we formulated rules to systematically compare several scenario’s.
We formulated the following scenario’s based on consecutive skipping exon rules:
1. All splice variants including 64 exons, skipping 1 exon (65 splice variants)
2. All variants including 63 exons, skipping 2 consecutive exons (64 splice variants)
63. All splice variants including 2 exons, skipping 63 consecutive exons (3 splice variants)
64. All splice variants including 1 exon, skipping 64 consecutive exons (2 splice variants)
We started with one exon skipping in the first scenario, and ended with 64 consecutive skipping exons in scenario 64. For FBN1 we analyzed model 1, 2, 3a and 3b, 4a, 5 and 6.
Table 5 presents the results for the FBN1 gene models.
| Model 1 | Model 2 | Model 3a | Model 3b | Model 5 | Model 6 | reduced Model 5 | |
|---|---|---|---|---|---|---|---|
| # of SV | 8 | 1 | 8 | 8 | 36 | 6 | 10 |
| log L | 202 | -5975 | -5996 | -5981 | -5732 | -4976 | -5704 |
| # params | 2746 | 3 | 13 | 13 | 41 | 11 | 15 |
| AIC | 5088 | 11957 | 12018 | 11988 | 11546 | 9975 | 11438 |
| BIC | 10973 | 11963 | 12046 | 12015 | 11634 | 9998 | 11470 |
# of SV=Number of splicing variants; log L=log likelihood;
# of params=Number of parameters; AIC=Akaike information criterion; BIC=Bayesian information criterion.
Model 1=Mclust model; Model 2=One splice variant; Model 3=Known splice variants; Model 5=Known and high mixture proportions splice variants; Model 6=Manually selected splice variants the .a and .b define normal model or the extended model respectively
Table 5: FBN1 Model results.
Opposite to the previous two genes the hierarchical cluster analysis found 8 clusters. However similar to the hierarchical cluster analysis of SLC2A10 and TGFβR2 non of these clusters reflected recognizable splice variants. The average of these clusters followed the trend of all observed patients. If we assumed one splice variant in this gene, we observed AIC /BI C values of 11957/11963. The AIC /BI C did not improve if we assumed the known splice variants (model 3a and 3b).
We used different scenario’s to estimate the AIC and BI C of all possible splice variants (model 4a). The best performing scenario, based on the lowest combined AIC and BI C values (12419 and 12574), was the scenario consisting of 67 splice variants skipping 22 consecutive exons.
We tried to improve the model with known splice variants (model 3a) by adding the splice variants with the highest proportion of the 64 different scenario’s (model 5). This optimized model consisted of 36 splice variants. When we reduced the number of splice variants to the 10 splice variants with the highest prevalence in model 5 (reduced model 5 in Figure 4), there was a small improvement in AI C and BI C values.
The predominant splice variant in model 5 and the reduced model 5 was the splice variant with 64 exons present, skipping exon 25. This variant is responsible for the drop in expression as presented in figure 4. This model improved the AI C and BI C values of the known variants model to 11546/11634.
We tried to manually estimate splice variants in this gene. This model with 6 splice variants had best AI C/BI C values. The 6 splice variants were new not existing variants based on the high and low points in exon expression.
We based our splice variation model on the assumption that the mean expression is equal for all exons included in a splice variant and zero for exons excluded in the variant. Because we developed our models based on microarray data we had to deal with background noise existing in the data.
In contrast to the hierarchical cluster analysis (model 1) we assumed a single mean expression over all exons in a splice variant. Therefore our model is more restrictive than the hierarchical cluster analysis models, which allows different mean expression values for exons in a splice variant. We think that these restrictions are valid be- cause our model follows the biological process of synthesis of an RNA-molecule in contrast to the hierarchical cluster analysis models. The frequency that pre-mRNA is transcribed from the DNA is identical for each pre-mRNA, regardless of the splice variant. Pre-mRNA’s still include introns and exons and is identical for each splice variant. The exons to be retained in the mRNA are determined during the splicing process. The expression of each exon is determined by the times the exon is included in each splice variant and the amount of splice variant produced. In our model we tried to estimate these parameters.
Marfans Syndrome is a clinical defined syndrome with dilation of the aorta as the most serious complication. Mutations in FBN1 are the most important criteria for the clinical Marfans Syndrome diagnosis [20,21]. Aorta pathology is also caused by mutations in other genes, including TGFβR2 and SLC2A10 [22]. Mutations in TGFβR2 lead to Loeys-Dietz Syndrome and mutations in SCL2A10 to Arterial Tor- tuosity Syndrome Arterial. All of these syndromes are related to fibrilin-1 and the TGF-β pathway. Marfans Syndrome is genetically caused by misfolding of fibrillin-1. Fibrilin-1 is encoded by the FBN1 gene. Fibrilin-1 in turn binds a latent form of TGF-β. TGFβR2 is involved in the TGF-β pathway by binding TGF-β. The role of SLC2A10 in the TGF-β pathway is less clear but it is well known to be associated with upregulation of the TGF-β pathway [23,24]. At this moment we do not know the impact of splice variants on the function and/or structure of proteins. We hypothesize that the splice variants most common in SLC2A10 and TGFBβ2 are transcribed in non-functional proteins, and therefore alter expression of the TGF-β pathway. The most common splice variant for FBN1 in our sample was a variant without exon 25. Mutations in this specific exon are well known to be associated with neonatal Marfans Syndrome, which is the most severe Marfans Syndrome form, but apparently lack of exon 25 expression is important for adult Marfans Syndrome as well.
In this manuscript we used a systematic approach to determine the probability of the presence of splice variants. The number of splice variants in our model is depending on the number of exons of the gene. For small genes we analyzed all possible combinations of exons. This resulted in a set of 2E possibilities, with E the number of exons of the gene. The set of splice variants included biologically highly improbable splice variants (e.g splice variants where only the first and the last exons were present). The entire set of splice variants was relatively small; therefore the computational implications were minor. The biologically unlikely splice variants were given a low prevalence in the analyses. When the gene-size increased, and the number of all possible combinations became too big to analyze, we turned to a scenario-based method.
In this method we systematically searched for splice variants based on predetermined rules. The disadvantage of this method is that we do not analyze all possible splice variants. In practice we can however often exclude a number of biologically unlikely splice variants by well defined splice variant selecting rules.
We developed a model to estimate the probability of the presence of specific splice variants. In this analysis we found four possible splice variants, not yet present in gene-databases, that might be present in SLC2A10, TGFβR2 and FBN1 in Marfan patients. Further research must be undertaken to confirm that these splice variants are actually present in this patient population.