Journal of Clinical Toxicology
Open Access

An Advanced In Silico Model to Optimize the Pharmacokinetic Studies ON ²⁵Mg ²⁺-Releasing Porphyrin-Fullerene Nanoparticles in Brain Ischemic Disorders

Author info »

Introduction

Development of a pharmacologically suitable, i.e., safe and effective, nanocarrier of Mg²⁺ ions was caused by the recent discovery of biophysical control of energy production in mitochondria through the so-called magnetic isotope effect of magnesium-25. It has been proven that only the magnetic isotope of magnesium ²⁵Mg²⁺ is a specific hyperactivator of most Mg²⁺ dependent reactions of ATP synthesis in the cell. It is noteworthy that the hyperactivation of energy metabolism by ²⁵Mg²⁺ ions requires an insignificant amount of these ions and takes place even in the absence of oxygen (deep tissue hypoxia).

Thus, the desired application of the described physical/biophysical phenomenon would be to correct the reduction of ATP production in tissues during hypoxia of any nature. To meet these expectations, a new pharmaceutical preparation based on a porphyrin-containing fullerene "ball" C₆₀ (porfilerene-MC16 or PMC16) has been proposed [1,2]. Both the substrate and oxidative phosphorylation pathways are Mg²⁺ dependent pro-cesses and, therefore, can be accelerated up to 2.5 times by ultramicro amounts of ²⁵Mg²⁺, the only magnetic isotope of magnesium, in contrast to the nonmagnetic isotopes 24Mg²⁺ and 26Mg²⁺ [3]. Simple “endosmotic pressure” causes the replacement of one Mg isotope by another (all of them are stable) in the active site of the Creatine Kinase (CK) [4]. This contributes to the manifestation of the magnetic isotope effect of ²⁵Mg²⁺, which, as shown to date, is an important hyperactivating element of magnesium-dependent control of ATP synthesis [3-6]. This makes the targeted delivery of the aforementioned magnetic isotope (nuclear spin +5/2, magnetic moment 0.85 of Bohr magneton, proportion in the natural mixture of isotopes 11%) to cells/tissues affected by hypoxia a really important pharmacological task. Nanoparticles capable of exchanging Mg²⁺ ions may be a suitable means of such delivery.

The particles are characterized as being low in toxicity (LD50=896 mg/kg, rats, i/v), amphiphilic (water solubility 430 mg/ml, pH 7.40), capable of clustering, and are membranotropic particles with a size of 1.8 nm based on fullerene C₆₀ [1,2]. This new drug, which has noticeable cationic properties (Figure 1), is a monoadduct of iron-containing porphyrin with the classic buckminsterfullerenebuckminsterfullerene (C₆₀)-2-(butadiene-1-yl)-tetra-(o-γ- aminobutyryl-o-phthalyl)-ferroporphyrin. Based on the synthesis methodology, it was named "Porfillerene-MC16" or PMC16 for short (Figure 1).

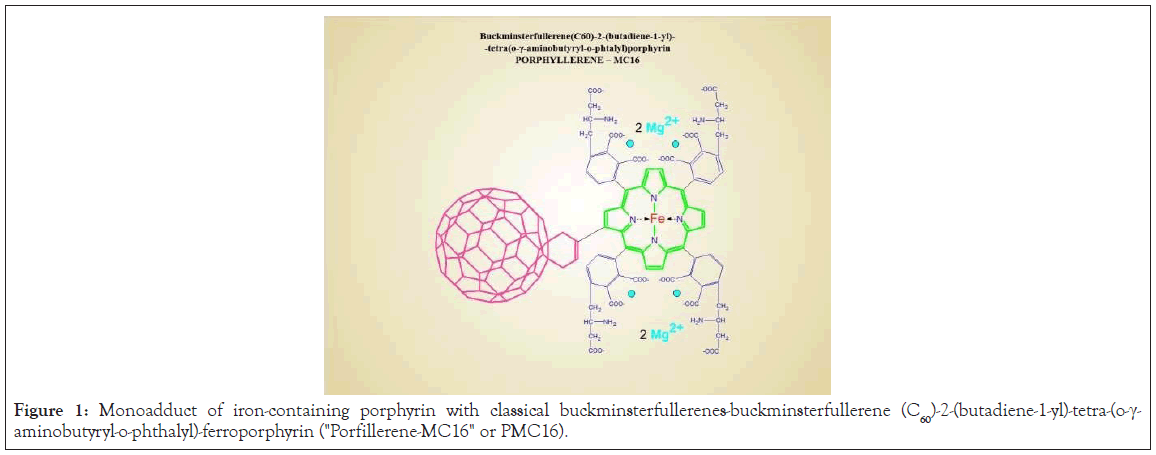
Figure 1: Monoadduct of iron-containing porphyrin with classical buckminsterfullerenes-buckminsterfullerene (C₆₀)-2-(butadiene-1-yl)-tetra-(o-γ- aminobutyryl-o-phthalyl)-ferroporphyrin ("Porfillerene-MC16" or PMC16).

You can expect this drug to fulfill at least two desires. First, its unique structure could allow the drug to serve as a nanocation exchanger both in vitro and in vivo as a result of "smart release" of magnesium in case of hypoxia-induced acidosis. Secondly, the porphyrin domain of PMC16 may provide tissue selectivity in relation to interaction with cell specific porphyrin receptors located on the mitochondrial membrane of myocardiocytes, where this has already been proven [7- 9], but also on the membranes of other cell types, and in particular, cells of the brain that have undergone oxygen starvation. This will allow for a truly targeted delivery of drugs to the area of hypoxia in the case of ischemic stroke. Considering the particle size of PMC16 (1.8 nm), drug penetration into mitochondria looks realistic [1,2]. The pharmacokinetics of PMC16 and the recognition of the drug by the receptor can facilitate or prevent this.

Noteworthy, the cation-exchanging nanoparticles (PMC16 family members) we’re taking here for granted as the “safe-n-stable” adducts of fullerene-C₆₀ are all known water soluble products with the marked antioxidant, i.e., potentially antihypoxia, properties for themselves-even once applied unloaded by any metal ions [10-13]. Thus, amphiphilic fullerene-containing compounds are, most likely, capable to emphasize the magnetic isotope effects of ²⁵Mg²⁺ on ATP-synthase and nucleotidyl kinases reaching both ATP hyperproduction and an oxygen consumption decrease [11,12] so beneficial for neuroprotection in the hypoxia-damaged brain tissue regions. The main directions in the modern pharmacology of fullerenes are associated with the problem of targeted drug delivery, since the possibility of these membranotropic nanoagents have already been shown to serve as specific carriers for organic/ bioorganic drugs [14,15].

However, as far as we know, with the exception, according to Sarkar, et al. [1], no in vitro and in vivo studies of the cation exchange activity of fullerene C₆₀ derivatives have been carried out. In view of this, based on the already known data describing the experimental pharmacokinetics of PMC16 for the mitochondria of myocardial cells, it is possible to simulate In Silico-the processes of targeted drug delivery, which is very promising for optimizing the program of preclinical studies of the drug, incl. for other nosologies.

At the same time, it should be noted that, in the absence of any studies known to us on modeling the pharmacokinetics of targeted delivery of nanopreparations based on fullerene-porphyrin adducts, the creation of In Silico models of the pharmacokinetics of targeting and selective accumulation of PMC16 nanoparticles is extremely important for optimizing further research in this area and possesses all the necessary novelty and relevance.

Talking about the direct and obvious practical benefits that are expected to be obtained through the proper use of mathematical modeling in determining the plan for pre-clinical studies of antihypoxic drugs, which in itself, undoubtedly, should be noted, such modeling is an essential requirement for optimizing the research plan for all new drugs. In particular, the applied pharmacological potential of such an approach based on the In Silico computational experiment can be perceived as an "encouraging break-through" for creating a new element in the strategy of preclinical studies for the prevention and/or correction of metabolic disorders of cerebral ischemia, based on the introduction of paramagnetic isotopes of bivalent metals, released and delivered by amphiphilic nanocation exchangers belonging to the superfamily of PMC16 (C₆₀-porphyrin) nanopar-ticles [16]. There is also one specific point we should not forget talking of an applied valid ity of In Silico research in molecular pharmacology/toxicology as a whole: A variable and con-traversal bioethical problems could be better resolved while the In Silico studies would 6 of 34 allow to avoid some certain experimental efforts in a course of in vivo segments of preclinical trials [17]. This should be also correct for the early steps of the new pharmaceuticals clinical trials and related research. The so-called "sovereign trend" in the computational modeling of pharmacological processes within the framework of the modern preclinical research paradigm has already had a significant impact on the development of drugs in experimental neurology and neuropharmacology [18-20]. This correlates with the PubMed statistics showing a noticeable increase in the number of publications on the above issue [21]. This work is part of a broader study devoted to the development of a new nanopharmacological approach to the prevention and treatment of local hypoxia syndrome of ischemic cerebral stroke by targeted delivery of ²⁵Mg²⁺ cations to the area of cerebral infarction through targeted delivery of porphyrin-fullerene nanoparticles as membranotropic carriers that release ²⁵Mg²⁺.

Materials and Methods

In Silico platform

To study the behavior of our model in the parameter space, we apply the theory of nonlinear dynamical systems and use a method known as "parametric analysis". In synergetics, it is more often called "bifurcation analysis". This method is effective for studying complex nonlinear processes in nonequilibrium systems of various types: Physical, chemical, social, biological, etc., according to their mathematical models. Here ‘s’, ‘D’, and e parameters were not calculated but given within the stated ranges, which were used to calculate the variables in question (C_A and C_B-concentration of РМС16 nanoparticles in the blood flow and the intercellular space, respectively). Thus, the behavior of the model with different combinations of parameters was investigated. The system of ordinary differential equations (1-8) was obtained by an analytical method based on the published data of biomedical studies of fullerene-porphyrin nanoparticles releasing ²⁵Mg²⁺ for the treatment of local hypoxia in the field of medical nanopharmacology and was simulated in MATLAB language in MATLAB/SIMULINK environment version 2021b. To solve the system of differential equations, the Runge-Kutta method of medium order was applied using the ode45 solver. The data presented in T_1/2=9, 0 hours, Tmax=25 hours, С₀=62 μg/ml. For the parameters, arbitrary values were varied. The program code is shown in Figure 2 and it is given in an additional file (see Supplementary file).

Figure 2: The code of the basic module of the In Silico computer program for the pharmacokinetics of targeted delivery of fullerene-porphyrin nanoparticles releasing ²⁵Mg²⁺ for the treatment of local hypoxia is shown in a vectoral format.

Due to the reasons we have given above it makes no sense to present some parameters in a separate table. The charts given in the article contain the required characteristic curves and are a much better representation of the meaning and the results of our research. The logics of Figure 2 is to present the original code of the software to satisfy the requirement of the editorial.

One of the most intriguing, truly attention catching, makes of this work relates to a specifically the autonomous matter of the computational approach we proposed. Thus, In Silico platform is not about either to describe or treat the experimental data derived from the extensive and costly full-scale preclinical (clinical) trial. Instead, this entirely about how to predict, i.e., how to reveal pre impirico a highly probable patterns of pharmacokinetic processes based on available information regarding the known nanoparticle properties, disease model morphophysiological signs, tissue hypohia molecular and cellular pathogenesis mechanisms, etc. Once succeeded, this approach is capable to provide with a reliable “navigator” information for further use in the optimized design of preclinical research multidisciplinary protocols. A mere need for getting such a specific In Silico paradigm was, in fact, shown and clearly expressed in several studies [22-29] including the ones devoted to fullerene containing nanoparticles in the mammalian tissue hypoxia and brain research [30]. Likewise, some current developments in molecular kinetics computational models operates with both Gomperrtzian and non-Markov’s population dynamics equation systems [31], which is a rather promising tool that has been brought to the In Silico focused nanopharmacology community.

Experimental verification

Nanoparticles: Water soluble samples of PMC16-RX were kindly provided by a courtesy of Dr. N. Amirshahi, Amir Kabir University of Technology, Tehran, Iran.

Animals: Wistar Albino Glaxo male rats, 180-220 g, were kept under a standard vitaminized diet, starving for 24 hrs before the experiment. Three animals per each experimental point, 5-6 repetitions for every measurement were carried out.

NP administration: 1.0 mg/kg and/or 20.0 mg/kg of NP was administered to rats in a single i.v injection. Solvent: 15 mM Tris- HCL (pH 7.80). Animals were decapitated 12 hrs after injection, brain tissue samples were removed and homogenized in 5-7 vols of 20 mM Tris-HCL (pH 8.0)/10 mM MgCl₂/1.5 mM NaCl/2.0 mM EDTA/25 mM sucrose/2.0% Triton X-100 (v/v). Potter glassteflone homogenizer, 1,800 rpm (+4⁰C), has been employed.

Brain homogenate treatment: To isolate the cytosol fraction (S125), the carefully washed homogenates were subjected to ultracentrifugation at 125,000 g, 4 hrs, +4⁰C, Spinco L5-65B Ultracentrifuge (Beckman, USA), rotor SW 27.1. Supernatants (S125) were carefully collected, protein measurements were performed by a routine Bradford colorimetric method.

S125 samples were mixed with 10 vols of ice-cold acetone followed by an overnight incubation at +4⁰C. The resulted pellets were precipitated at 20,000 rpm, 20 min, +4⁰C and removed. Supernatants were collected for further use in UV-VIS spectrophotometry and CZE studies.

To elucidate the target product extractability degree, the acetone precipitated dry pellets were dissolved in 15 mM ammonium phosphate (pH 8.80)/0.1% SDS/2.5 mM EDTA/1.0% 2-mercaptoethanol (20:1, v/w) with a consequent sonication treatment at 60 KHz, 40⁰C, 60 min, followed by the below specified Capillary Zone Electrophoresis (CZE) analysis.

Ischemic stroke model: The filament insertion based modeling of ischemic stroke in rats was performed, using the middle cerebral artery occlusion as described by Leone, et al. [31].

CZE procedure: Acetone-soluble S125 extracts were concentrated in a rotor evaporizer to the final volume of 0.2 mL followed by addition of 30 mM ammonium-phosphate (pH 8.80), 25:1 (v/v). 10 μL of a sample was inserted into the P/ACE MDQ Plus CZE Analytical System (ALGIMED, Belarus) coupled to the UVVIS 770 KS detector, 440 nm monochromatic filter (Prince Technologies, Netherlands) with a following 10 min run at +6⁰C: Quartz (50 μ diameter/7.5 cm effective length) capillaries packed with the UV-transparent silica saturated by SJX40 electrolyte-pH 8.80 (SCIEX BV, Netherlands), 115V/60 Hz/300 W per cap. Data acquisition unit: DAX DATE 220 LK (SCIEX BV, Netherlands). The corresponding calibration chart is stated in Table 1.

Results

In experiments on laboratory animals for the case of myocardial infarction, certain significant characteristic features of the pharmacokinetics of PMC16 were found, which make it unique and super promising in comparison with conventional drugs, not belonging to the nano-group drugs. One of these proven experimentally remarkable features of PMC16 nanoparticles is their long-term retention in tissue and especially inside the mitochondrial membranes of myocardiocytes, the reasons for which have not been studied, but the most likely explanation for this phenomenon may be the presence of protein receptors in these membranes with high affinity for PMC16, i.e., in the presence of signaling proteins in the cell membranes, which are responsible for the selective recognition of the drug. Simple signaling proteins of this type are known for a number of porphyrin metabolites [32-36].

Another important experimentally [37-41] discovered feature is that the accumulation of particles in the ischemic zone occurs even at low concentrations of PMC16 in the blood. As for the methods of targeted delivery themselves, to date, in relation to this very peculiar group of nanodrugs, exclusively magnetic and immunological methods have been studied [22-24]. As far as we know, with the exception of works [1,2], no studies of the cationexchange activity of fullerene C₆₀ derivatives have been carried out. On the other hand, this is exactly the activity that is required for the delivery of ²⁵Mg²⁺ cations to hypoxic cells and tissues. According to our point of view, the aforementioned targeted delivery can help compensate for hypoxia-induced ATP loss due to the known ²⁵Mg-de- pendent hyperactivation of both oxidative and substrate ADP phosphorylation pathways during ATP synthesis in the cell [3-6]. As can be seen from the data presented due to its cationic properties, PMC16 has the necessary potential as a carrier of Mg²⁺ ions. It is noteworthy that this drug can act as “smart nanoparticles” capable of releasing magnesium in response to an increase in the acidity of the medium [1,2]. At the same time, it was found that PMC16 clustering is also pH dependent. These facts look attractive in light of the data on the molecular pathogenesis of hypoxia, according to which tissue acidosis is a direct natural metabolic consequence of hypoxia of any kind [2,6]. Thus, when (²⁵Mg) PMC16 is administered in vivo, acidosis-induced ²⁵Mg²⁺ release can be expected. The amphiphilic nature of this drug [1,2] also supports these expectations, since the dual solubility of a drug usually correlates with its membranotropic properties [9,22].

In addition, the absence of allergenic properties and inflammatory effects found in most of the ever studied fullerene derivatives [29,30] and, as a rule, a high degree of “biocompatibility” [31] allows experimental studies of the safety and pharmacological activity of PMC16 in vivo. All these specific features of PMC16, despite the extremely poor knowledge of the underlying mechanisms, must be taken into account when creating mathematical models 8 of 34 underlying In Silico, using a system of equations demonstrating similar dynamics. And further, such equations, using well-known mathematical tools, can be brought to a fairly good agreement with the available experimental data. This is the main idea of the fundamental solution of the In Silico problem of a “magic bullet” for the targeted delivery of nanopreparations of the PMC16 type to the problem area under the conditions of the complexity of so little knowledge of the physicochemical mechanisms of the entire set of processes in the body.

We are talking about the targeted delivery of the drug to the hypoxia zone: Whether it is the myocardial region, the focus of ischemic stroke in the brain, or any other area of the body or organ where cells lack oxygen, including its complete absence. The In Silico pharmacokinetics of targeted delivery of PMC16 is based on the idea of using the peculiarity of the course of the pathologies under study, which, as is known, the body responds to the development of the inflammatory process to the pathologies that accompany heart attacks. And for the vessels penetrating such zones of inflammation, an increased distance between epithelial cells is characteristic, which is not observed outside the zone of inflammation. So the body locally reacts to the problem and increases the throughput of the vascular sections in the hypoxic zone in order to provide an increased flow of substances from the blood that is necessary to eliminate the problem situation. Thus, PMC16 nanoparticles, even when assembled into clusters, will selectively penetrate into the inflammation zone, where they will be captured by the cell membrane, even in the absence of any driving force, except for those arising from Brownian motion.

When a nanopreparation is injected directly into the circulatory system, a single-compartment model of pharmacokinetics is quite sufficient. The two-compartment model and multi-compartment models at this stage will only make the initial system of differential equations heavier, and it makes sense to resort to them at the stage of In Silico detailing if you need to describe in more detail other subtle processes or change the method of drug administration. Nevertheless, for convenience of understanding, we represent our system in the form of two chambers separated by an impenetrable partition, which is a surface of area S with a local porosity in some area with a total area s as shown in Figure 3.

The two areas that are separated by a septum are the circulatory system and the extracellular space. Let us designate these chambers by the letters A and B. Simultaneous administration of the drug at a concentration of C into the circulatory system at the time t0=0 will increase its concentration in the blood (chamber A) from 0 to СА(0)=С, while at this moment in the intercellular space (chamber B) the concentration of the drug will be CB(0)=0. Assuming in our case the system is closed, according to the second law of thermodynamics, it will tend to equilibrium, leveling the concentrations between the chambers, and a substance flow proportional to the ratio of the pore areas and the partition area s/S will pass through the surface S. The driving force behind this process is the concentration gradient. Then the flow of matter passing from chamber A to chamber B according to Fick's 1st law can be written in algebraic form by the formula:

where W is the substance flux (PMC16 nanoparticles), s/S is the ratio of the area of the vascular system in the area of inflammation to the total area of the circulatory system of the body, D is the diffusion coefficient, grad C is the concentration gradient. For three dimensional space

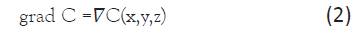
In our case, for a point (global) model, the spatial coordinate is not essential and is not used, and formula (1) can be rewritten as:

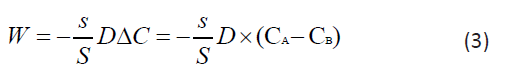
Where С^A is the concentration of nanoparticles in the blood, C^B is the concentration of nanoparticles in the intercellular space of the inflammation zone. The balance equation for any moment of time t ∋ (0, t), can be written as follows:

In this case, it follows from Eqaution (3) that at a certain point in time, the concentrations in both chambers become equal and the flow of nanoparticles from the blood into the intercellular space will stop. However, in practice this does not happen, since it was already noted above that the transfer of PMC16 to the ischemic zone continues even at extremely low concentrations of the drug in the blood. This can only be the case if the substance is continuously removed from zone B. The gradient will then remain positive as long as there is substance in Chamber A, down to the lowest concentrations. In this case, the system becomes open, and the balance equation (4) is not observed in it. The reason for this behavior of the system is the membranotropy of PMC16, which, being actively absorbed by cells, is excreted from the intercellular space at a certain rate e. Then the change in CB concentration in chamber B can be written in differential form as follows:

It should be borne in mind that in chamber A the concentration of C^A also decreases with some total rate v due to various reasons: Selfdecay, phagocytosis, absorption by other cells, natural elimination, etc., which can be written down:

Then the basic system of ordinary differential equations of the point mathematical model can be written in the form:

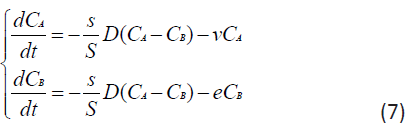
Taking into account that the rate of elimination from the intercellular space in the area of inflammation e due to the capture of PMC16 nanoparticles by the mitochondria of cells is much higher than the rate of elimination of nanoparticles from the circulatory system v, in a first approximation it can be neglected. Then system (7) can be rewritten as:

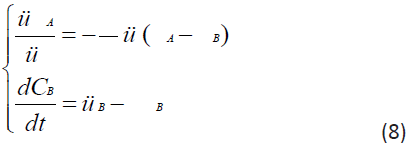
By specifying the initial conditions at t₀=0, C_A(t0)=C is the initial dose of the preparation, C_B(t₀)=0, can solve the Cauchy problem for the system of ordinary differential equations (8). The resulting system of equations was simulated in MATLAB/SIMULINK version 2021b and studied for different model values of the parameters s, D, e. The curves of the calculated dependences C_A(t), C_B(t) are shown in a series of Figure 4. In this paper the investigation of non-equilibrium systems within the synergetic approach is applied, which is known as the ‘parametric analysis’.

Figure 3 shows a general view of the pharmacokinetic curves of PMC16 concentrations in the circulatory system (C_A)-black line and intercellular space of the inflammation focus (C_B)-red line with a single intravenous/ intra-arterial injection of the drug, calculated In Silico for arbitrary values of the parameters s, D, e at the time interval t: (0, T), T=20 hours, T_1/2=9, 0 hours.

Figure 3: The graphic model of the system in the form of two chambers A and B separated by an impenetrable partition, which is a surface of area S with a local porosity in some area with a total area s. Ca and Cb are the concentrations of nanoparticles in the chambers.

The goal of (Figure 4): We demonstrate the general view of pharmacokinetic curves the model gives. This view corresponds to their classical shape. As can be seen from the figure, the graph of the calculated graph of pharmacokinetic dependences quite adequately corresponds to the general form of pharmacokinetic curves, with the only feature that the decrease in concentration in the intercellular space is more gentle (red curve C_B), in comparison with the classical curves of pharmacokinetics. This means that the drug is retained in the blood much longer (dynamics of the C_A curve) and the transport of the drug into the extracellular space does not stop until the smallest drug concentration in the bloodstream.

Figure 4: General view of the pharmacokinetic curves of PMC16 concentrations in the circulatory system (CA)-black line and intercellular space of the inflammation focus (C_B) red line after a single intravenous/intraarterial injection of the drug, calculated In Silico for arbitrary values of the parameters s, D, e over a period of time t: (0,T), T=20 hours, T_1/2=9, 0 hours. Note: C (A), C (B). s=0.09, S=1, D=5, v=0, e=0.27.

In this sense, the parameter ‘s’ plays an important role in reflecting the supply of the preparation from bloodstream to intercellular space. However, it is not definitive in describing the experimentally identified [21] specific of the targeted РМС16 delivery, including the peculiarities of its retention in ischemized cells, even in the case of low initial doses of the injected preparation. The problem is solved via the entire mathematic of the model.

Prior to reaching the cells hit by ischemia, the preparation must somehow proliferate into the intercellular space. The blood vessel wall is the first barrier the PMC16 must penetrate to get into the intercellular space. The parameter ‘s’ is introduced to narrowly characterize this particular phase of the pharmacokinetic process. No doubt, there exist various mechanisms of the penetration of medications into the intercellular space, and indirectly they are just as well accounted for by ‘s’. It is known that in the inflammation zone the organism reacts by increasing the intercellular distance between the epithelial cells of the vessels in order to provide for enhanced supply/ejection of the necessary substances and metabolic products, and this mechanism may be considered definitive for the delivery of PMC16. Thus, ‘s’ simultaneously describes the degree of inflammation, which may be considered to be proportional to the area of the pores wide enough for the penetration of the PMC16 nanoparticles and their clusters circulating in the bloodstream into the inflammation zone. The concentration gradient (3) is the driver of this flow (or a flow of any other substance), and the РМС16 supply would have been terminated fairly fast a the concentrations balance each other, were it not for the mechanism which we call the cellular pump, thanks to which РМС16 is being intensely eliminated from the intercellular space, being actively absorbed by cell in the state of hypoxia. Therefore, the concentration gradient, and, consequently, the flow of РМС16 to the inflammation zone (in contrast to other substances) is sustained up to extremely low concentrations in the bloodstream, which corresponds to the experimental picture [21].

Preliminary data from our in vivo studies confirm the adequacy of the presented in this article In Silico model (Tables 1 and 2). A detailed report on the results of these experiments will be given in our next article, which will be devoted to improving the model presented in this article and linking In Silico to experimental data using transfer functions. Thus, we can investigate both the penetration of PMC16 nanoparticles into the tissues and the distribution of their components, including the released Mg²⁺. Parameter ‘s’ is obviously also a characteristic of the inflammation severity of ischemic stroke. However, the principal goal of this parameter is to characterize the degree of the local porosity increase of the vascular bed in the inflammation area due to the increase of the intercellular space of vascular cells and, consequently, the amount of the penetrating (into the intercellular space of the inflammation area) PMC16 nanoparticles from the blood flow. In case of no inflammation s=0, meaning that PMC16 nanoparticles do not penetrate the intercellular space. With its increase the ‘porosity’ of the vascular bed in the inflammation area increases in proportion to the inflammation degree, which leads to the increased drug inflow from the blood stream. The exact dependence of the ‘s’ parameter value on the level of inflammation in case of an ischemic stroke has to be researched separately and is not within the scope of this study.

Table 1: The internal standard contents as correlated to absorbance of CZE-revealed target compound (PMC16-RX, Rt=7.0 min).

Table 2: BBB permeablity for PMC16-RX and the drug intralization in brain cells.

We might stress it out here that a particular advantage of this In Silico path would allow to avoid a routine post-experiment data description/treatment [8,9,11,12,21,20] due to computational prognostic power realized by an interactive taking into account of known PMC16 pharmacology, ²⁵Mg-MIE mammalian tissue hypoxia and BBB functional parameters-including the stroke related peculiarities [13,20,22,24,28]. This itself has been deliberately done to make an intriguing forthcoming comparison of our In Silico derived prognosis (A) with the further experimental data (B), whatever difference and/or similarity between (A) and (B), would be found out then. So the next anticipated step in our ongoing work is expected to be a testing quest for a key point of present study which is a prognostic validity of our In Silico method.

This is exactly how could we verify both scientific and applied pharmacological significance of the latter. Meanwhile, however, we are describing here a new mathematical model which is nothing but a preliminary move toward the next, experimental, phase of this current multi-stage research. After all, a specification of this In Silico paradigm is, of course, mandatory to establish/defend a priority for it. The results of In Silico parametric analysis of the pharmacokinetic model are shown in Figures 5-7.

Figure 5: Behavior of pharmacokinetic curves with changing parameter s (local size of the inflammation zone during hypoxia) and fixed D and e. Note: C (A), C (B). s= (0.01, 0.03, 0.05, 0.07, 0.09), S=1, D=1, v=0, e=1.

Figure 6: Changes in PMC16 concentrations in blood (black line) and intercellular space (red line) with changes in diffusion coefficient D at fixed s and e. Note: C (A), C (B). s=0.03, S=1, D= (0.2, 0.6, 1.1, 4.1, 8.2, 2.2, 6.3), v=0, e=1.

Figure 7: Changes in the concentration of PMC16 in the blood (black curve) and the intercellular space of the inflammation zone (red curve) with a change in the rate of uptake of nanoparticles by cells e of constants ‘s’ and ‘D’. Note: C (A), C (B). s=0.03, S=1, D=1, v=0, e= (0.01, 0.03, 0.05, 0.07, 0.09).

In Figure 5 with fixed D and e, the behavior of the pharmacokinetic curves with a changing parameter s is shown. The dependences shown in the graph reflect the behavior of the system (changes in the concentrations of PMC16 in the blood and intercellular space of the inflammation zone) depending on the local size of the inflammation focus.

In Figure 5 we study the response of the model to the inflammation level. Following parametric analysis of information systems method, we fix the values of parameters ‘D’ and ‘e’ and change only parameter ‘s’. Thus, we study how the inflammation degree influences the model behavior. The parameter "S" represents the area of the vascular system of a living object and is designed to adjust to the appearance of a laboratory animal for in vivo research. As you know, the area of the circulatory system is different in different biological species. In this paper, we do not touch this aspect and take S=1 everywhere.

It can be seen from the figure (black curves CA) that with an increase in the size of the inflammation focus, the concentration of PMC16 in the blood decreases faster (the curve falls the steeper), the larger the size of the inflammation zone, which quite naturally and adequately reflects the behavior of the real system. In the case of a large volume of inflammation, the drug remains in the blood for much less time. In this case, in order to achieve a continuous therapeutic effect, the frequency of injections and/or the dose must be increased. The behavior of the PMC16 concentration curves in the intercellular space of CB (red curves) shows that the larger the size of the inflammation focus, the sharper the increase in the PMC16 concentration in the intercellular space of the focus at the time of its introduction, but also faster and more abruptly decreases. It is important to note that the maximum concentration of the drug in the intercellular space of the inflammation zone is also strongly depends on its size. Analytical data presented in Figure 5 are important for the selection of individual therapy algorithms.

Figure 6 shows the behavior of the system for different ‘D’ and fixed ‘s’ and ‘e’. As you know, the diffusion coefficient is numerically differentiated in different organs and tissues. As can be seen from the graphs shown in the figure, when ‘D’ changes, the dynamics of the system also changes. Thus, by changing ‘D’, it is possible to tune In Silico selectively for hypoxia in different organs and tissues. Here we study the impact of diffusion (parameter ‘D’) on the model behavior. It’s important to consider the diffusion rate, because it’s important to know if the model is applicable to various tissues and organs and if its prognostic and analytical properties can be enlarged. Moreover, the histology of the stroke area is inhomogeneous. This is also considered through ‘D’. The diffusion rate is different in different organs and tissues. There are methods to measure it. Diffusion is a process of the penetration of molecules and atoms of a substance between atoms and molecules of another substance, the process leading to the balancing of concentration over the volume considered. The measured Apparent Diffusion Coefficient (ADC) is a quantitative parameter of diffusion (the motion of water molecules) into tissues and is calculated using the Diffusion-Weighted Imaging an MRI (DW-MRI) [42]. The DW-MRI is an indispensable instrument for studying the central nervous system, and apply to the identification of acute ischemic attacks as well as to the differentiation of brain tumors or the diagnosing of brain infections. DW-MRI relies on the chaotic Brownian motion of water molecules in the space outside and inside of cells or inside of blood vessels. The density and size of tissue molecules, along with the presence of damaged membranes, create resistance to the motion of water molecules. This resistance may be estimated quantitatively with the help of the measured ADC. The units are mm2/c. There is no unity of opinion on the subject of the range of normal diffusion, but the respective values should depend on the specific organ and the pathology studied [43]. Some useful ADC values can be found in [44-46]. In our study, the parameter ‘D’ is preparation-specific to PMC16 and its numerical value does not have to match the ADC value found in the literature for organs and tissues, but there may be a reasonable correlation between them. Additional in vitro and in vivo studies are needed to assess the correlations exactly, for a PMC16 preparation-specific diffusion rate, as well as to obtain exact numerical values for ‘D’. It is also drug-specific. It means we speak about the diffusion of some substance in some media. In our model ‘D’ is a drug-specific to PMC16 and to the selected organ (in this case brain) diffusion rate. It should be taken into account that brain is histologically inhomogeneous, especially if we speak about the structure of the ischemic stroke focus. This is a separate complex issue.

In Figure 7 shows the change in the concentration of PMC16 in the blood (black curve) and the intercellular space of the inflammation zone (red curve) with a change in the rate of uptake of nanoparticles by cells e of constants ‘s’ and ‘D’. Here we study the impact of parameter ‘е’ characterizing the absorption rate of PMC16 nanodrug by a cell. Measuring parameter ‘е’ at fixed ‘S’ and ‘D’, we study pharmacokinetic properties of the model. The biophysical and biochemical properties of the process are complex, not yet fully investigated and are specific for the drug. We don’t consider parameter ‘e’ a constant. PMC16 has a high level of membrane tropism. The rate of its absorption by cells will probably depend on the degree of ischemia and the need of the cell in ATP, which the cell compensates due to the released PMC16 ²⁵Mg²⁺ nanoparticles. The behavior of the curves confirms the experimentally found above-described unique properties of PMC16 to selectively enter the hypoxia zone even at the lowest blood concentrations. It can be seen from the graphs that the selective flow of nanoparticles into the intercellular space of the inflammation zone continues to the lowest concentrations of nanoparticles in the blood. As you can see, the lower the concentration in the blood, the more the black and red curves are attracted to each other as the concentration decreases. Moreover, the lower their concentration in the bloodstream decreases, the higher the specific proportion of particles drawn into the intercellular space of the hypoxia focus. Moreover, for a certain e, the model shows “sticking of curves” (top pair of graphs), corresponding to optimal therapeutic conditions, when the entire drug is absorbed by cells with the greatest efficiency. Here we also observe the longest retention of nanoparticles both in the circulatory system and in the intercellular space of the hypoxia focus.

The parameters ‘D’ and ‘e’ are introduced to tune In Silico to the organ, for which hypoxia is being simulated, and the corresponding rate of the absorption of the preparation. Thereby, the universality of the model is ensured as well as its applicability to various locations of hypoxia such as the brain, the heart muscle, etc. As noted earlier, parameter e characterizes the rate of drug uptake by PMC16 cells. And this process gives, in addition to diffusion, an additional driving force for the directed transfer of PMC16 nanoparticles to the hypoxic zone. Such a process can be compared to a pump that is additionally turned on, enhancing the transfer of matter. But it should be noted that this transfer is enhanced selectively, and not for any substance circulating in the blood, but only for PMC16 nanoparticles. It can be assumed as an explanation for the described phenomenon that the rate of absorption of PMC16 by cells depends on the degree of their need for oxygen for the production of ATP, which is a magnesium-dependent process, lacking which the cells strive to replenish it with the greater intensity, the more they lack oxygen. And ²⁵Mg²⁺ is the only source for the production of ATP under anaerobic conditions. Therefore, the greater the requirement of cells for ATP, the more intensively they absorb PMC16 nanoparticles, which are practically the only source of ATP production under hypoxic conditions. A major key point of experimental verification for such an In Silico paradigm as ours is a prove for both BBB permeability and the brain cell intralization as regards specifically to PMC16 nanoparticles. This task has been solved as seen from Tables 1 and 2. Noteworthy, the brain stroke damaged tissue areas were also accessible for PMC16 (Table 2).

Thus, a relatively low “mass amount level” of the NP intralization in rat brain cells (Table 1) might have nothing to do with the agent’s anticipated pharmacological impact since the latter would be determined by extraordinary ATP overproduction anyway, i.e., by the direct and inevitable result of ²⁵Mg²⁺-MIE phenomenon. Needless to outline that the drug intralization itself is a true priority in advanced pharmacokinetics studies.

A simple one-step ultracentrifugation of the mammalian tissue homogenates, usually pre-treated with Triton X-100, 105,000 g-150,000 g (Metods), are to provide a reliable separation of cytosol from the cell organelles as well as from ribosomes, ribosome subunits, and membrane debris. Being a total cytoplasm compounds solution, the S125 fraction, therefore, is a perfect material to use in drug-cell intralization research [3,4,10]. Although the results presented looks quite self-sufficient, it should be nonetheless stated that the resolution and sensitivity of our CZE procedure are good enough to find out low but detectable level of PMC16-RX rat brain uptake estimated as 4.0- 8.0 ng per 1.0 mg of total S125 protein. This amount of NP is detectable 12 hrs after a single i.v injection of the agent. A CZE/PMC16-RX calibration data beyond (Table 1). So, the blood-brain barrier penetration for xenobiotic tested has been clearly shown (Tables 1 and 2).

Discussion

The paper [21] features the data from an in vitro and in vivo study experimentally modelling the syndrome of medication-induced hypoxia in myocardium and presents a broad spectrum of research into PMC16, including an experimental investigation of the PMC16 and its metabolites’ pharmacodynamic and pharmacokinetic for various organs. Amirshahi, et al. [21], find the data on the tissuespecific accumulation of PMC16 in rats after a single injection. Experiments register selective accumulation and protracted retention of non-metabolized molecules of the preparation exactly where the hypoxia was modelled in the aforementioned paper-in the myocardium cells. Similar dynamics were found under the conditions of the multiple injections course of ultra-low doses of PMC16, as evidenced by the data in [21]. At the same time, the total absence of long-time capture of PMC16 was observed in dealing with other tissues (liver, lungs, kidneys, skeleton muscles) [21]. The In Silico mathematical model presented in this paper yields completely adequate results on the qualitative level. This model adequately reflects the essence of the process discovered and helps to understand it mathematically. Despite the good performance of the model presented in this article in the first approximation, one cannot but agree that it also has objective drawbacks, although the predictive and descriptive capabilities demonstrated by In Silico pharmacokinetics of targeted delivery of fullerene-porphyrin nanoparticles that release ²⁵Mg²⁺ are described in this work, in a characteristic sense, are quite high. The model, built on the onecompartment principle, is, of course, adequate only for two of the parenteral modes of drug administration: Intravenous and intraarterial. It cannot numerically (and perhaps even characteristically) describe other methods, since it does not include the drug-specific features of other modes of administration.

Data from full-scale in vitro and/or in vivo experiments will be required at a certain stage to adjust the In Silico model to actual study objects. Normally this is performed through dynamic characteristics, which supplement the system of equations. These functions connect the values of the internal theoretical parameters ‘s’, ‘D’, and ‘e’ to the actual objects. After that we can speak about the correlation of the numerical values of parameters to the actual objects and simulation studies, as well as on the complex combination of calculational and full-scale experiments to optimize pre-clinical studies.

Due to the fact that In Silico is built in a global (point) model, it also does not take into account for the spatial factors of the spread of processes and substances. For these reasons, it is unsuitable for spatial modeling of hypoxia processes and diseases arising from this. But being a pharmacokinetic model, it is not required to solve such problems. For the same reason, its capabilities are severely limited for solving pharmacodynamic problems. Undoubtedly, with the accumulation of experimental data, In Silico capabilities will improve. First of all, this concerns an increase in the compartmentalization of the model to take into account both additional methods of drug administration and the ways of its elimination. It is also of interest to supplement the capabilities of the model with pharmacodynamic and other modules, primarily due to the ability to describe the features of more subtle and complex intracellular Mg-dependent processes in relation to the therapeutic features of nanopreparations of the PMC16 line and taking into account the pathophysiology of ischemic stroke as described by Fursov, et al. [32]. The main reason for the hindering development of the model is the lack of experimental data obtained in vitro and in vivo, as well as the poorly studied at the biomedical level of a large number of processes and phenomena occurring in the body. The development of In Silico is a related, but a separate fundamental task, the value of which is to identify the methods of mathematical description of very complex processes occurring in the body and to further implement In Silico models to solve applied tasks. To verify our In Silico platform, the experimental estimation of PMC16 nanoparticles in the rat brain cytosol fraction has been proposed.

Conclusions

1. Based on the analysis of literature data on the known properties of the promising antihypoxic nanopreparation PMC16, which is a monoadduct nanoparticle of iron-containing porphyrin with the classic buckminsterfullerenebuckminsterfullerene (C₆₀)-2-632 (butadiene-1-yl)-tetra-(o-γ- aminobutyryl))-ferroporphyrin, releasing ²⁵Mg²⁺, the unique antihypoxic effect of which is based on the magnetic isotope effect of the only magnetic isotope ²⁵Mg²⁺ in the family of magnesium isotopes, we for the first time obtained an elegant system of second-order equations, which was the basis In Silico of drug-specific phar-macokinetics of targeted delivery of nanoparticles and selective PMC tissues subjected to hypoxia.

2. This mathematical model, despite its apparent simplicity, simultaneously describes several complex processes occurring during the transport of a nanopreparation to the hypoxia focus, and reflects the main drug-specific features of the pharmacokinetics of targeted delivery and selective accumulation of PMC16 in organs and tissues subjected to oxygen starvation (hypoxia). The model does not contradict the main characteristic features of pharmacokinetic curves in one or two compartment interpretation, and can be effective for computational experiments and the development of scenarios for PMC16 preclinical studies as applied to the treatment of ischemic stroke, myocardial infarction and a number of oncological diseases for which Mg-dependent processes are import

3. From a practical point of view, a novel In Silico systematic stematic directory proposed might indicate a perspective for clear and essentially simplified plan making required to design an optimized protocol suitable for the (²⁵Mg²⁺) 4PMC16-related preclinical research program. This supposed to be realized by taking into account an anti-hypoxia pharmacological potential of these medicinal nanoparticles in the brain ischemic disorders (stroke) 652 studies.

Author Contribution

Dr. V.V. Fursov: Mathematical modeling per se, data analysis, conclusions, design of the manuscript. Prof. Dr. D. A. Kuznetsov: Biomedical aspects of the brain ischemia models, data collection and analysis, antihypoxic NP specificity and magnetic isotope effects to take into account, conclusions.

Acknowledgements

Prof. Dr. Eleonora M. Koltsova, Prof. Dr. Alexander G. Majouga and Ms. Daria I. Zinchenko, Mendeleev University of Chemical Technology of Russia, Moscow, Russian Federation, are to be sincerely thanked for their consultations and for their encouraging comments on this work.

Conflict of Interest

The author declared no conflict of interest.

Ethical Approval

The study was approved by the ethical review board at the Pirogov Russian National Research Medical University (protocol No. 140 of 15 December 2014) and the local committee for surveillance of the maintenance and use of laboratory animals (protocol No. 13/2020 of 08 October 2020, protocol No. 24/2021 of 10 December 2021).

Funding

Work was supported by grant of Ministry of Science and Higher Education of Russian Federation No 075-15-2020-792 (Unique identifier RF----190220X0031).

References

1. Sarkar S, Rezayat SM, Buchachenko AL, Kuznetsov DA, Orlova MA, Yurovskaya MA, et al. New water soluble porphylleren compounds. United States patent application US 12/123, 285. 2008.

   [Google Scholar]

2. Sarkar S, Rezayat SM, Buchachenko AL, Kuznetsov DA, Orlova MA, Yurovskaya MA, et al. Use of a magnesium isotope for treating hypoxia and a medicament comprising the same. United States patent application US 12/123, 245. 2008.

   [Google Scholar]

3. Buchachenko AL, Kouznetsov DA, Arkhangelsky SE, Orlova MA, Markarian AA. Spin biochemistry: Magnetic 24Mg-²⁵Mg-26Mg isotope effect in mitochondrial ADP phosphorylation. Cell Biochem Biophys. 2005;43(2):243-251.

   [Crossref] [Google Scholar] [PubMed]

4. Buchachenko AL, Kouznetsov DA, Arkhangelsky SE, Orlova MA, Markarian AA. Spin biochemistry: Intramitochondrial nucleotide phosphorylation is a magnesium nuclear spin controlled process. Mitochondrion. 2005;5(1):67-69.

   [Crossref] [Google Scholar] [PubMed]

5. Buchachenko AL, Kouznetsov DA, Orlova MA, Markarian AA. Magnetic isotope effect of magnesium in phosphoglycerate kinase phosphorylation. Proc Natl Acad Sci. 2005;102(31):10793-10796.

   [Crossref] [Google Scholar] [PubMed]

6. Buchachenko AL, Kouznetsov DA, Breslavskaya NN, Orlova MA. Magnesium isotope effects in enzymatic phosphorylation. J Phys Chem B. 2008;112(8):2548-2556.

   [Crossref] [Google Scholar] [PubMed]

7. Kano K. Molecular complexes of water-soluble porphyrins. J Porphyr Phthalocyanines. 2004;8(02):148-155.

   [Crossref] [Google Scholar]

8. Hudson R, Mallroy C, Darnell S, Smith KM. Porphyrin conjugates in photoimmunotherapy. Br J Cancer. 2006;93:1442-1450.
9. Pawar R, Avramoff A, Domb AJ. Nanoparticles for crossing biological membranes. Nanotechnologies for the Life Sciences: Online. 2007.

   [Crossref] [Google Scholar]

10. Bucyachenko AL, Tyutyunnik VM. New frontiers in gene chemistry. In: Prospective areas of recearch in science and technology. 2021:144-158.

    [Crossref]

11. Liu Y, Zeng S, Ji W, Yao H, Lin L, Cui H, et al. Emerging theranostic nanomaterials in diabetes and its complications. Adv Sci. 2022;9(3):2102466.

    [Crossref] [Google Scholar] [PubMed]

12. Pinheiro RG, Coutinho AJ, Pinheiro M, Neves AR. Nanoparticles for targeted brain drug delivery: What do we know? Int J Mol Sci. 2021;22(21):11654.

    [Crossref] [Google Scholar] [PubMed]

13. Sharoyko VV, Shemchuk OS, Meschcheriakov AA, Vasina LV, Iamalova NR, Luttsev MD, et al. Biocompatibility, antioxidant activity and photoprotection properties of C₆₀ fullrene adducts. Nanomedicine: Nanotechnology and Medicine. 2021;40:102500.

    [Crossref] [Google Scholar]

14. Andrievsky G, Klochkov V, Derevyanchenko L. Is the C60 fullerene molecule toxic?! Fuller Nanotub Carbon Nanostructures. 2005;13(4):363-376.

    [Crossref] [Google Scholar]

15. Pantarotto D, Tagmatarchis N, Bianco A, Prato M. Synthesis and biological properties of fullerene-containing amino acids and peptides. Mini Rev Med Chem. 2004;4(7):805-814.

    [Crossref] [Google Scholar] [PubMed]

16. Buchachenko A. Magneto-biology and medicine. InMagneto Biol Med. 2014;1-236.

    [Google Scholar]

17. Naz S, Bashir F. Dual use research of concern. Pak J Med Res. 2019;58(4):153-154.

    [Google Scholar]

18. Augsburger JJ, Chow CML, Dyer V, Roussel MF. Translating science into survival. In: St. Jude's Children's Research Hospital Report. 2016:6-55.
19. Bozic I, Nowak MA. Resisting resistance. Ann Rev Cancer Biol. 2017;1(1):203-221.

    [Crossref] [Google Scholar]

20. Gusev EI, Skvorcova VI. Ishemiya golovnogo mozga. Medicina. 2001.
21. Amirshahi N, Alautdin RN, Sarcar S, Rezayat SM, Orlova MA, Trushkov IV, et al. 713 Porphyrin-fullerene nanoparticles in the hypoxic cardiopathies treatment. Russian Nanotechnol. 2008;3:99-109.

    [Crossref] [Google Scholar]

22. Piotrovsky LB, Kiselyov OI. Fullerenes in biology: On the way towards nanomedicine. Rostok Publication, St. Petersburg. 2006.
23. Suarez M, Verdecia Y, Illescas B, Martı́nez-Alvarez R, Alvarez A, Ochoa E, et al. Synthesis and study of novel fulleropyrrolidines bearing biologically active 1, 4-dihydropyridines. Tetrahedron. 2003;59(46):9179-9186.

    [Crossref] [Google Scholar]

24. Tabata Y, Ikada Y. Biological functions of fullerene. Pure Appl Chem. 1999;71(11):2047-2053.

    [Crossref] [Google Scholar]

25. Waugh T, Telashima H. Mitochondria. Research Triangle Publication. Raleigh-Durham, NC. 2004.
26. Gergely M, Lakatos I. Molecular and cellular cardiology. Alba Regia: Budapest-Szeged. 1999.
27. Pawar R, Avramoff A, Domb AJ. Nanoparticles for crossing biological membranes. Nanotechnologies for the Life Sciences: Online. 2007.

    [Crossref] [Google Scholar]

28. Mahato RI. Biomaterials for delivery and targeting of proteins and nucleic acids. CRC Press. 2004.
29. Baierl T, Seidel A. In vitro effects of fullerene C60 and fullerene black on immuno-functions of macrophages. Fullerene Sci Technol. 1996;4(5):1073-1078.

    [Crossref] [Google Scholar]

30. Mellul M. Cosmetic make-up composition containing a fullerene or mixture of fullerenes as a pigmenting agent. United States patent US 5,612,021. 1997.

    [Google Scholar]

31. Leone JE, Narayanan PV. Catheter system having fullerenes and method. United States patent US 6,468,244. 2002.

    [Google Scholar]

32. Fursov VV, Fursov IV, Bukhvostov AA, Majouga AG, Kuznetsov DA. In Silico studies on pharmacokinetics and neuroprotective potential of 25Mg2+: Releasing nanocationites-background and perspectives. Pharmacogenetics. 2021; 24:155.

    [Google Scholar]

33. Bray D. Limits of computational biology. In Silico Biology. 2012;12(1-2):1-7.

    [Google Scholar] [Crossref]

34. Maynard AT, Roberts CD. Quantifying, visualizing, and monitoring lead optimization. J Med Chem. 2016;59(9):4189-4201.

    [Crossref] [Google Scholar] [PubMed]

35. Wooller SK, Benstead-Hume G, Chen X, Ali Y, Pearl FM. Bioinformatics in translational drug discovery. Biosci Rep. 2017;37(4):BSR20160180.

    [Crossref] [Google Scholar] [PubMed]

36. Rajah GB, Ding Y. Experimental neuroprotection in ischemic stroke: A concise review. Neurosurg Focus. 2017;42(4):E2.

    [Crossref] [Google Scholar] [PubMed]

37. Fatima S, Quadri SN, Parveen S, Beg S, Barkat MA, Samim M, et al. Nanomedicinal strategies as emerging therapeutic avenues to treat and manage cerebral ischemia. CNS Neurol Disord Drug Targets. 2021;20(2):125-144.

    [Crossref] [Google Scholar] [PubMed]

38. Paul S, Candelario-Jalil E. Emerging neuroprotective strategies for the treatment of ischemic stroke: An overview of clinical and preclinical studies. Exp Neurol. 2021;335:113518.

    [Crossref] [Google Scholar] [PubMed]

39. Skvortsov VS, Ivanova YO, Voronina AI. The bioinformatic identification of proteins with varying levels of post-translational modifications in experimental ischemic stroke in mice. Biomed Khim. 2021;67(6):475-484.

    [Crossref] [Google Scholar] [PubMed]

40. Kazemzadeh H, Mozafari M. Fullerene-based delivery systems. Drug Discov Today. 2019;24(3):898-905.

    [Crossref] [Google Scholar] [PubMed]

41. Glielmo A, Husic BE, Rodriguez A, Clementi C, Noé F, Laio A. Unsupervised learning methods for molecular simulation data. Chem Rev. 2021;121(16):9722-58.

    [Crossref] [Google Scholar] [PubMed]

42. Sener RN. Diffusion MRI: Apparent Diffusion Coefficient (ADC) values in the normal brain and a classification of brain disorders based on ADC values. Comput Med Imaging Graph. 2001;25(4):299-326.

    [Crossref] [Google Scholar] [PubMed]

43. Haaga, Robert J, Daniel TB. CT and MRI of the whole body. 2017.
44. Helenius J, Soinne L, Perkiö J, Salonen O, Kangasmäki A, Kaste M, et al. Diffusion-weighted MR imaging in normal human brains in various age groups. AJNR Am J Neuroradiol. 2002;23(2):194-199.

    [Google Scholar] [PubMed]

45. Annet L, Duprez T, Grandin C, Dooms G, Collard A, Cosnard G. Apparent diffusion coefficient measurements within intracranial epidermoid cysts in six patients. Neuroradiology. 2002;44:326-328.

    [Crossref] [Google Scholar] [PubMed]

46. Gubskiy IL, Namestnikova DD, Cherkashova EA, Chekhonin VP, Baklaushev VP, Gubsky LV, et al. MRI guiding of the middle cerebral artery occlusion in rats aimed to improve stroke modeling. Transl Stroke Res. 2018;9:417-425.

    [Crossref] [Google Scholar] [PubMed]