Journal of Depression and Anxiety
Open Access
ISSN: 2167-1044
ISSN: 2167-1044
Review Article - (2014) Volume 3, Issue 2
The Center for Epidemiologic Studies Depression Scale (CES-D) is a widely used screening test for depression symptomatology in population studies. Publications have dealt with the psychometric properties of the instrument. Until now, no published work has examined the how questionnaire items are handled in data processing protocols. This technical report introduces the “CESD-Flag” macro algorithm using SAS® 9.3 syntax. The main contribution of the statistical program in this report is to provide data managers with a program that creates five CES-D flag variables to help identify the level and location of missingness in CES-D related data. The paper highlights implications from how data editing algorithms handle missing or inconclusive responses to CES-D questions. If absolute transparency should be encouraged as a desirable goal, then the methodology used to “clean” CES-D data should be provided along descriptive statistics for the five flag variables (measure of item incompleteness) created by the CESD-Flag program. The assignment of responses through non-evidence based algorithms merits further attention as the use of CES-D continues to proliferate internationally.
Keywords: CES-D; Data management; Scoring scale; Allocation; Missing
The Center for Epidemiologic Studies Depression Scale (CES-D) has been, is, and continues to be widely used as a screening tool for depression symptomatology in population studies. A search of the term “CES-D” in search engines turns up thousands of manuscripts where the scale has been used as the outcome variable, a predictor, or covariate. Attesting to its popularity, the survey instrument has recently been tested in: French samples [1]; Rwanda genocide survivors [2]; Germans [3]; Fiji samples [4]; Chinese in the mainland [5]; Canadians [6]; people in India [7]; Japanese [8]; the Spanish version in people in the United States (US) [9]; in Turkish [10]; Iran [11]; and many others. Despite any possible limitations with the instrument as it regards the measurement of depression symptomatology across diverse cultural groups, it appears its use will continue to grow.
Hundreds of years ago it was written that: There is no more delicate matter to take in hand, nor more dangerous to conduct, nor more doubtful in its success, than to set up as a leader in the introduction of changes. For he who innovates will have for enemies all those who are well off under the existing order of things, and only lukewarm supporters in those who may be better off under the new [12].
This project follows in the footsteps of the many others who have sought to introduce changes with the potential to improve quality of research on human health [13]. The goal of this technical report is to highlight the logic implicit in data processing protocols that alter missing (i.e., no response recorded for question) or illogical (i.e., recorded information do not correspondent to possible values) responses. This is important because data editing processes have the ability to affect the quality of statistical products and theoretical meaningfulness of quantitative results. The main goal of this paper is not to discuss how missing data should be handled in regression analysis. Instead, the focus is on how data creators should document the management of missing responses in order for secondary data users to understand the quality of the data. Although the goal could be reached by using anyone of a multitude of popular scales, the CES-D is used as an example in this paper. What is said about data processing protocols for the CES-D applies to all survey scales and questionnaire items. The paper hopes to contribute to health research literature dealing with psychological assessment by primarily arguing that radical clarity in the procedures undertaken for creating data are necessary if research is to detect a more probable truth as it distances itself from absolute uncertainty. In contribution towards these goals, the project presents and makes available a novel statistical program (originated by author without the use of any external sources) to help data managers create five different variables that can help secondary data user understand the withinperson level of in-completeness for the full CES-D scale and its four sub-scales separately.
At the most fundamental level, investigating human health through statistical techniques (e.g., using regression equations) requires numerically coding their behaviors, perceptions, physical attributes, and environments. In order for the legitimacy of statistics to be employed in analyses, human behavior must be converted into a numerical existence—i.e., the abstraction of the physical world must occur with the use of numbers. Numbers attributed with meaning are then explored in a world of equations where results from samples are used to infer population characteristics or where statistical significance is inferred typically using frequentist views on probabilities. Unfortunately, a study participant could be born into the world of numbers through ambiguous mechanisms and careless documentation. Paying attention to how information is handled at the most early stages of data creation is crucial to the value of any subsequent work because the quality of data influences the potential value of results.
Contamination of numerical representation could be said to occur when data creating procedures assign responses or alter original answers given by a study participant. The power of mathematics in statistics hangs on the fragile presupposition that equation users will respect the various assumptions when modeling data. The assumption that ‘data accurately represents’ the phenomenon under study is as fundamental to statistical analysis as the assumption that humans need oxygen to survive—its absence precludes the value of any subsequent work. Transforming physical reality into a numerical existence requires data creators to navigate a complex labyrinth between truth and possibility. There is an abundance of challenges present when attempting to abstract human reality from numbers.
No deeper taboo exists in quantitative research than the idea that a dataset has been manipulated to meet the needs of the researcher. Previous events show this is possible [14] and arguments have been made that the need to publish or perish in academia may exert influences in the formation of data and results [15,16]. Evidence exist that the percentage of researchers who engage in questionable practices is not low [17] and that deliberate fraud with data falsification is ongoing [18-21]. For example, a recent case provided evidence that a cardiovascular researcher with over 500 papers to his name made use of fictitious data [22]. Some have argued that a hypercompetitive scientific climate encourages poor scientific practices and that consistent methodological rigor is necessary to transform the system [23].
Eloquent expositions have been made to argue that self-correction in scientific practices are not always the default as scientific credibility fluctuates over time and place [24]. The production of high quality and transparent data is crucial for maintaining high levels of scientific credibility. For example, undisclosed data management procedures may create the irreproducibility of studies fuelling the perpetuation of unchallenged fallacies. In the absence of the principle that ‘seeking the truth is the number one priority over any other goals’ [24], important decisions may be seen as trivial by untrained data managers or principal investigators without extensive experience in data creation. The pursuit of scientific discoveries should engender a deep sense of responsibility in the creation of data. The lack thereof can lead to events like those of the stem cell researchers who fabricated data in publications presented in the reputable journal of Science [25]. Even astute readers are now advice to view any article with a modicum of healthy skepticism [26,27]. It should be noted that threats to scientific integrity by a few can influence the opinion of research in many [28].
Non specialist may take it as an article of faith, that data creators are skilled, ethical, and highly precise technicians who simply oversee the organic birth of digital information as data gets entered from a paper survey or electronic source. As a reminder that researchers are capable of deception like any other human beings, [29] wrote that the “stereotype of a fully rational and objective ‘scientific method,’ with individual scientists as logical (and interchangeable) robots, is self-serving mythology.” It may be that the strength to do right from philosophical principles pales in comparison to the more immediate and concrete pressures to survive in academia through publications [30]. The main assumption motivating this paper is that the scientific method offers the best option for understanding human behavior. Built on this is the view that quantitative research though statistical techniques are the most precise tools for digesting complex human data. On these two building blocks rests the axiom that most researchers genuinely seek the truth and wish to improve the world. It is only because such views form my disposition that a call for radical clarity is given in this paper.
This article only addresses the unintentional production of poor data quality through ill-informed data-editing protocols. In particular, the paper focuses on how mishandling unclear or missing responses to questions (i.e., handling of item missingness) can affect the quality of data. This is important because item missingness (i.e., lack of responses to survey questions) may be highly prevalent. Arguments that this is the case exist dating back decades [31]. The prevalence of missing data may be obscured by the lack of reporting. For example, some have shown evidence that about one third of epidemiological randomized trial studies in PubMed journals do not report the handling of missing data [32]. It should be noted that randomized clinical trials are considered by some as the gold standard for inferring causality in health related research. The inconsistency of discussing missing data in publications obligates this paper to assume that missing data are prevalent. The assumption can be supported by evidence. For example, researchers have argued that despite continuing methodological developments, missing data are usually inadequately handled in both observational and experimental research [33]. An investigation on top-tier publications found a high prevalence of partly missing outcome data, the avoidance of complete case analysis, and lack of reporting sensitivity analysis [33].
A review of 100 articles in cancer research showed that missing covariate data was a common occurrence and that describing the methods used to handle incomplete covariates was rare [34]. Others have investigated refereed educational journal publications and found that only 1 in 10 articles explicitly reviewed how missing data was treated and that only tree out of the 68 article in their investigation provide percentages of missing data [35]. The authors argue that the treatment and reporting of missing data is inconsistent [35]. Their work offers an elegant set of practical guidelines for addressing, explaining, and treating missing data in educational research [35]. This paper’s primary contribution is in providing a statistical program that can help quantify the level and location of missingness in the CES-D scale.
For many years, researchers have made calls for analysts to be explicit in reporting the presence of missing data and their analytical strategies applied [36]. Some researchers have been diligent in reporting the presence and treatment of missing data since the 1980s. For example, researchers studying depressive symptoms in young adolescents explained that in coding their scale; missing responses were assigned the mean score of the completed items [37]. Others have been confident enough in the integrity of their projects that they are forthright about level of missingness and treatment of data. For example, researchers investigating the perspectives of Parkinson’s disease spouses explained that a score was not given on a scale unless at least 75% of the items were answered—missing responses were estimated using the average of given responses within the scale [38]. Researchers studying suicidal behaviors in young adolescents reported the presence of missing responses and explained that zeroes were assigned to missing responses when at least 88% of the questions in a scale were given [39]. More recently, investigators using CES-D discussed that 8.7% out of 1,250 were missing [40]. The consistency of clear reporting on missing data may increase if journal editors and reviewer consistently ask the following questions when reviewing manuscripts: (1) Was missing data edited in the production of the factors under observation?; (2) Was item missingness properly handle during the data entry stage and properly documented with flag variables?; (3) Was item missingness handled during data creation or statistical analysis?
At no point is the falsification of data recommended in this manuscript. However, if the formation of a complete dataset is mandatory, then multiple imputation (MI) is the non-perfect but optimal solution. Although not fully reviewed in this paper, it should be noted that statisticians have advocated the use of MI [41]. Others have explained that MI has the ability to adequately reflect the uncertainty in analytic study results produced by item missingness [36]. Some have also pointed out that even though MI may be increasingly regarded as a standard method, aspects of its implementation do vary and authors rarely provided details in their approach [42] like underlying assumptions in MI used and how results may compare to other approaches such as complete cases analyses [43]. Even more technically, the use of fully conditional specification (FCS) (sometimes referred to as “chained equations”) and multivariate normal imputation (MVNI) has been compared with complete-case analysis to show that both FCS and MVNI are generally less biased than complete-case analysis [44].
Authors should continually be encourage to mention how data entry protocols handled missing, inconclusive, or illogical responses in the formation of their scale scoring algorithms. When no response is given to a survey question, the item is said to be “missing.” When a “don’t know” or “refused to answer” response is given, the item is said to be “inconclusive.” For example, when logical response values range from 0 to 9 and a value of 22 in entered during data processing, then the item is said to be “illogical”—outside the range of plausible values. Item non-response can be caused by various factors [45] and is not the main focus of this report. When the seminal paper on CES-D was published, Professor Radloff mentioned in passing that “the entire CES-D scale was considered missing if more than four items were missing” [46]. In other words, at least 80% of the 20 questions needed to have a logical value for a person to be assigned a CES-D composite score. Composite score refers to the total score which can range from 0 to 60 (20 items each ranging from 0 to 3). The main point here is that even from its inception, the originator acknowledged the fact that responses to CES-D items could be missing. In his work, Radloff appears to have left missing responses as zero (without inversion of positive affect items) and assigned composite score to individuals with at least an 80% level of completeness. Radloff may have failed to envision the massive success of his scale. He did not advice with great specificity how unclear responses in CES-D should be handled or what procedures should be deemed acceptable for creating a composite score.
Since then, researchers have been left to their devices to “fix” responses and score CES-D as they deemed most appropriate. Fix in this context refers to the fact that the “original” value entered for an item is changed through the use of some data-editing algorithm. Fixing items may be argued by some to be too closely related with the fabrication of information. Data editing is common and needed for the formation of complete data—where missingness is reduced through implicit or explicit data editing procedures. Low levels of missingness seen to be an informal prerequisite for inferential statistics where the population parameters can only be estimated using the randomness employed in the sample selection and not the non-randomness of item non-response. Since Radloff, few studies have described how responses are fixed, making it difficult to determine the heterogeneity of methods in the field and their effects on the meaning of findings. Discussing the treatment of data should not be accompanied by the risk of damaging the reputation of a dataset. Instead, it should be applauded and encouraged. A higher level of transparency and clarity should be expected and is practice in the field. For example, one publication did discuss the fact that a few study participants had missing responses for CES-D questions and that “cohort by gender by education means were substituted for missing data within the group” [47]. The main argument is that investigators should be forthright about any data editing methods employed in order to provide readers with the ability to decide for themselves if the approach merits confidence.
Why is there so much silence on the topic? Ideally, scientific research should be conducted in a ‘non-competitive world’ where absolute transparency is rewarded as a constellation of investigators pooled together their resources to advance the understanding of a particular topic. It may be argued, that all too frequently, the need to persuade others on the quality of data motivates writers to remain silent about ‘messy facts’ and focus on the positive attributes of a dataset. This approach serves well if the only goals are to publish and procure research funding. It may be argued that empirical research should be primarily motivated by the desire to improve knowledge. If improving research is challenged by the lack of transparency in the methods used to fix data, then the silence over how CES-D related data is cleaned should end. This argument applies to all surveys and items and only makes use of the CES-D by way of example.
The specific aim of this paper is to provide researchers with a statistical program that can be used to create multiple variables for ascertaining the level and location of missingness in the CES-D scale. The program provided with this manuscript (Appendix A) uses Statistical Analysis Software (SAS® 9.3) macro language. The macro should be applied to unprocessed (i.e., “raw”) data with no manipulation by data entry personal/device. Notes in the program explain each step. Explanations are given for each method as are the assumptions associate with the implicit logic being used to fix a missing, inconclusive, or illogical response in this report. The algorithm creates five “flag” variables to measure and locate item incompleteness and provides 10 alternate approaches for editing data—all of them make assignment of responses to study subjects through non-evidence based implicit logic which may be argued to be the prevalent approach for creating complete data. Presumably, most procedures for fixing CES-D items make use of some arbitrary method. No evidence has been formalized for how items should be handled. The main point is to be clear about what is being done and start a public discourse among experts on the issues related with the alternate coding schemes. The “%CesdFlags” SAS macro in Appendix-A may be a first step towards standardizing data management procedures for handling CES-D data and serve as example of how other scales should be treated in the literature.
Measure of incompleteness
In order to better understand how much information is missing, the %CesdFlags SAS® [48] 9.3 macro creates five “flag” variables: 1. CESD_Flags: A count of how many responses are missing within each person for the full scale 2. DEPRE_Flags: A count of how many responses are missing within each person for the depressed affect sub-scale (items 3, 6, 9, 10, 14, 17, 18) 3. POSIT_Flags: A count of how many responses are missing within each person for the positive affect sub-scale (items 4, 8, 12, 16) 4. SOMAT_Flags: A count of how many responses are missing within each person for the somatic activity sub-scale (items 1, 2, 5, 7, 11, 13, 20) 5. INTER_Flags: A count of how many responses are missing within each person for the interpersonal relations sub-scale (items 15, 19)
For all these variables, as the value of in the flag variables increase, the number of incomplete information increases within the person. For example, if CESD_Flags=3, it means the person has 3 unclear or missing responses from the 20 CES-D questions; if SOMAT_Flags=3, it means the person has 3 unclear or missing responses from the somatic activity CES-D sub-scale. The grouping of the sub-scales was established many years ago [49,50], more recently [6], and arguments for why these subscales are not stable between populations exist in publication [51]. The main point is to show that sub-scale missingness can be identified with the CesdFlags macro provided with this report.
The 5 flag variables can be used to explain the level and location of incompleteness in CES-D composite score. Journals should be encouraged to require that authors provide the sample mean, range, and standard deviation for the five flag variables. This would provide readers with an opportunity to gage the average level of data completeness in composite CES-D scores in the sample. Even more ideally, if researchers begin to report the descriptive statistics of the 5 flags, it may be possible to set “minimum threshold of completeness”—acceptable level of average missingness. Note that psychometric testing of CES-D infrequently discusses implications for validity and reliability of the instrument given the potential heterogeneity for the level and location of missingness possible in the scale. It may be that data management protocols produce complete but low quality data through non-evidence based procedures before regression analyses take place. The formation of the 5 flag variables may encourage data stewards to think about the methods they employ to edit responses to CES-D questions. If flag variables are left in the data, secondary data users could identify which items have been ‘fixed’ and decide to change back to missing for use with multiple imputation.
Transformations
The transformation of missing values can be done in a number of ways. In this paper, “transformation” refers to the changing of originally recorded values through the explicit and non-theory driven logic found in the %CesdFlags algorithm. The reader should note that the author advices against any form of data manipulation. Reliable, valid, and high quality data can only be obtained through the formation of good study design, implementation, and data processing protocols. Methods for employing transformations are only being offered to show how scientifically uninformed procedures can alter the meaning of scale composite scores through flawed and potentially unethical data manipulation. The transformations are discussed to critique their assumptions and disambiguate for non-experts how data creation protocols can influence the meaning of scale composite scores.
Figure 1 shows the theoretical model articulating how the quality of data can be affected through various mechanisms during data processing algorithm. The flowchart depicts a scenario where data is gathered using paper surveys. The use of computer devices to record data and their black-box-algorithms are beyond the scope of this project. The main point from Figure 1 is that using ad-hoc edits by data entry personnel may help produce complete data that is both nontransparent and creates ambiguous CES-D composite scores. Ad-hoc edits with no record of why changes were made should be avoided at all cost so that data quality is controlled under a rigorous and systematized environment. Using the macro presented in this paper can help produce complete and transparent data. The macro shows using systematized assignment protocols produce ambiguous CES-D composite scores. The only approach being advised by the author is entering data as it appears on the paper—this would produce transparent, incomplete, and non-ambiguous data that may be made generalizable by using multiple imputations in the treatment of missing values. The approach would allow secondary data users the ability to decide how to handle missing or ambiguous responses. The key argument is that the burden of proof, that the data was managed ethically and with the highest standards, rest with the data creator and then the data user. Response editing causes unquantifiable bias in the measure of depression symptomatology and limits the valuable psychometric properties of the CES-D. The chain of information supply should be transparent.
The simplest transformation is to simply treat all missing values as zeroes. This would assume that missing, don’t know, and refused values are equivalent to answering ‘rarely or none of the time’—no empirical evidence exist in publication to make such an assumption. The “transform to zero” approach may be common in practice— where non-academic data managers opt for the approach because the development of the programming syntax is the most manageable. Using the “zero transformation” is not advice as there is no way of knowing how a CES-D composite score with such a transformation differs from the ‘true’ responses the person would have given. The use of the zero transformation produces ambiguous CES-D composite scores which may be considered invalid, unreliable, and inappropriate.
There are more complex approaches to produce transformations. In addition to the zero transformation used in the %CesdFlags macro, three basic viewpoints are used to produce more transformation scenarios: (1) only those who offer 100% of answers merit a CES-D composite score (variable named CESD_100); (2) only those who offer at least 80% of answers merit a CES-D composite score (variable named CESD_80); and (3) even those who offer 0% of answers merit a CES-D composite score (variable named CESD_0). The %CesdFlags macro uses these three approaches to compute group average values to be used in the replacement of missing responses. By combining the three basic viewpoints and group average approach, a total of 10 scenarios are used to create different CES-D composite scores. Please note %CesdFlags does not include all possible methods for replacing missing values. For example, it does not use the popular approach of replacing missing item scores by using the ‘within-person item mean.’
One composite score is computed by using the zero transformation approach and three composite scores are created by only using the three basic viewpoints (i.e., CES_100; CESD_80; and CESD_0). Six composite scores are based on group averages as follows: transform missing values in those with at least 80% by using the group average computed by using those with a 100% level of completion (variable named g100_80); transform missing values even if 0% of answers were originally recorded by using the group average computed by using those with a 100% level of completion (variable named g100_80); transform missing values in those with at least 80% by using the group average computed by using those with at least a 80% level of completion (variable named g80_80); transform missing values even if 0% of answers were originally recorded by using the group average computed by using those with at least a 80% level of completion (variable named g80_0); transform missing values in those with at least 80% by using the group average computed from all those in the sample including subjects with a 0% level of completion (variable named g0_80); and transform missing values even if 0% of answers were originally recorded by using the group average computed from all those in the sample including subjects with a 0% level of completion (variable named g0_0).
To help the reader understand the complex combinations of scenarios, a conceptual Level of Manipulation Scale (LoMS) is used. Because we have ten possible scenarios, LoMS ranges from 1 to 10. The level of manipulation is said to increase as the LoMS score increases: when LoMS=1, CES-D composite score is the least manipulated; and when LoMS=10, the CES-D composite score is most manipulated. In LoMS order from 1 to 10 the scenarios fall from least to most manipulated as follows: CESD_100; CESD_80; CESD_0; CESD_Z; g100_80; g100_0; g80_80; g80_0; g0_80; and g0_0. The argument that the zero transformation (CESD_Z) contains the most manipulation is addressed in closing.
Synthetic data
The ten different CES-D composite scores produced through the various scenarios are discussed in detail below. In order to show the reader how the various approaches create noticeable differences, a synthetic dataset was created and used to produce descriptive statistics and linear regression results for all 10 scenarios. The synthetic data does not represent real people. The synthetic data was provided with this article was produce by the author for the instrumental purposes of this project. The data includes all 20 CES-D variables and the following covariates: sex (male=1); race (minority=1); SES (socioeconomic status high=1); and cancer (has cancer=1). Synthetic CES-D responses were assigned with the following general patterns: males report less depression symptoms; minorities report more depression symptoms; those with high SES report less depression symptoms; and those with cancer report more depression symptoms. These patterns are not meant to represent the literature—they were only created to show how their presence is captured differently under the various transformation scenarios. The only thing that really matters in the synthetic dataset is the pattern of missingness: females have less missing; minorities have more missing; those with high SES have less missing; and those with cancer less missing. These patterns of missingness are not informed by literature. The main point of the synthetic data is to provide the reader with a stable data source where the %CesdFlags program can be used to explore its effects on descriptive statistics and regression results.
Basic scoring schemes
Scoring where 100% complete (CESD_100): M i s s i n g , inconclusive, and illogical responses to CES-D questions could be left as they are—a “no modification” approach would be said to have been used. This approach renders the truest representation of data and simultaneously creates the largest number of people with missing CES-D composite scores. In practice, it may be rarely used. The “no modification” approach is advised because no assumptions are made about the items that could be fixed. The %CesdFlags macro creates the “CESD_100” variable and can be considered the most strict composite score of CES-D—where no assumptions are made since only real and clear answers are used and a composite score is created for people who have all 20 responses. Those with missing CES-D composite scores under the “no modification” approach could be assigned a score using maximum likelihood multiple imputation at the data analysis stage [52] or through more complex hot deck techniques [53].
Scoring where 80% Complete (CESD_80): Please note that the CESD_100 variable makes the least amount of assumptions of any of the composites scores computed by the macro. In contrast, CESD_80 assumes that a 80% item-response level is acceptable for assigning individuals a composites score. CESD_80 does not discriminate which 30% of items are missing presumably the missing items may differ between subjects. For example, Person-A may have a CESD_80 score of 10 and a 90% level of completeness (i.e., CESD_Flags=2), while Person-B may have a CESD_80 score of 10 and a 80% level of completeness (i.e., CESD_Flags=6). The items missing a response for Person-A may be completely different than the items missing for Person-B. The CESD_80 composite score would not account for the level and type of missingness. The level of uncertainty in the meaning of the CES-D composite score increases. Although it does not assign zero to ambiguous or missing responses, they are treated as zeroes in the computation of the composite score. This is important to understand because there are four CES-D items that require reverse coding. Assigning zeroes creates the ability to reverse these four items; however, when a zero is not assigned they remain unreversed. With either approach, fixing reversible items with zero or ignoring them increases the meaning of the final composite score. This approach is discouraged for use as the implications associated with the 30% level of incompleteness are unknown and the approach may create notable an unknown level of ambiguity in the score. This approach is very data driven and assumes those responding with at least 80% non-modified responses are truly representative of the individual and the survey item.
Scoring where 0% Complete (CESD_0): Those with no answers get a zero and all the others are assigned composite scored using available answers. Despite these seemingly dangerous approaches to managing responses, CESD_100 and CESD_80 may be argued to be rarely used. It may be that more ‘liberal’ techniques like CESD_0, which increase the level of uncertainty in the meaning of the composite score by making use of more assumptions, are more frequently used. More liberal approaches for assigning responses to CES-D survey items are presented below—although their used is not advised. They are presented because they may be the most widely used and readers should be made aware of some of the assumptions associated with the different methods.
Group Average with CESD_100 (gAvrg_100)
The variable “gAvrg_100” is calculated using CESD_100. The variable gAvrg_100 represents the group average computed by only using individuals who were originally assigned non-ambiguous scores for each of the 20 items (i.e., 100% of all items). More clearly, the mean from all the cases where 100% of non-ambiguous responses are given is divided by 20. In formula form: gAvrg_100=(group mean from all those with 100% completion ÷ 20)=gAvrg_100. More technically, only those with an original within-person 100% level of completeness (i.e., flags variable equals 0) are used to compute gAvrg_100.
Group Average with CESD_80 (gAvrg_80)
The variable “gAvrg_80” is calculated using CESD_80. The variable gAvrg_80 represents the group average computed by only using individuals who were originally assigned non-ambiguous scores for at least 16 out of the 20 CES-D items (i.e., 80% of all items). In other words, the mean from all the cases where at least 80% of nonambiguous responses are given is divided by 20. In formula form: gAvrg_80=(group mean from all those with 80% completion ÷ 20). In technical terms from the %CesdFlags program, only those with at least an original within-person 80% level of completeness (i.e., flags variable < 4) are used to compute gAvrg_80.
Group average with CESD_0 (gAvrg_0)
The variable “gAvrg_0” is calculated using CESD_0. The variable gAvrg_0 represents the group average computed by using all the individuals in the data where ambiguous scores are treated as zeroes (i.e., can be as low as 0% of all items). More directly, it takes the mean from all the cases in the data set since even those with no responses are assigned a zero and then divides that number by 20. Note ambiguous or missing responses are not transformed to zeroes but are treated as such (by default of ignoring their missingness) only for the computation of composite score. In formula form: gAvrg_0=(group mean from all and even if 0% completion ÷ 20). In this scenario, even those with an original within-person 0% level of completeness (i.e., flags variable can equal 20) are used to compute gAvrg_0.
Transforming with zero
The main difference between this approach and the used to compute CESD_0 is in how missing items are treated for those who have 0% of responses were missing or ambiguous responses are treated as zero for the calculation of the composite score. Missing, inconclusive, and illogical responses to CES-D questions are assigned a zero —a “zero modification” approach would be said to have been used. This approach fixes items by assigning them as a “rarely or none of the time” response. The zero modification approach assumes that missing responses implies the individual rarely identifies with the statement in the question—this applies to items that need reverse coding. There are no clear reasons or evidence for why items needing fixing should ever be manipulated in such a way. It is difficult to quantify how the zero transformation approximates, if at all, the ‘true’ response of the individual. The %CesdFlags program refers to the CES-D composite score using the zero transformation as “CESD_Z”—with this variable, all individuals will appear to have given a valid response during the interview process. Fixing responses with zeroes creates a complete dataset. However, the price for eradicating missingness is the production of a CES-D composite score which may be said to be highly ambiguous as it would be difficult to determine how it reflects reality.
The main point is that data editing procedures are employed and the information is undisclosed to subsequent data users, secondary data users will not have any way of knowing that a non-evidence based and non-probability approach was used to compute what may be considered invalid, unreliable, and inappropriate CES-D composite score. Investigators unsure of the procedures used to score CES-D composite scores in their data should declare it by signaling they are unable to descriptive the 5 CES-D flag variables created by the %CesdFlags program. The literature review in the background may allow for a defensible argument to be made that it is safe to assume that in most cases, observational studies using CES-D will have some level of missingness in the CES-D items. Thus, a dataset where all subjects have a zero for their flag variables should be treated with caution.
Assign “gAvrg_100” to missing if at least 80% answered (g100_80)
The CES-D composite score referred to as “g100_80” is calculated by assigning missing, don’t know, and refused answers the group average score obtained by using only those with 100% non-manipulated completion. The gAvrg_100 score is only assigned to missing answers if at least a 80% completion (i.e., have < 4 flags). In other words, items with ambiguous responses are assigned the gAvrg_100 value. The g100_80 represents the CES-D composite score where items with ambiguous responses are assigned the gAvrg_100 value where the original withinperson level of completeness was at least at 80%. Even though the approach may be considered somewhat conservative, the selective eradication of missingness via a “conservative group average” value produces CES-D composite scores which may be said to be ambiguous as their representation of the ‘truth’ is unknown.
Assign “gAvrg_100” to missing even if 0% answered (g100_0)
The CES-D composite score referred to as “g100_0” is calculated by assigning missing, don’t know, and refused answers the group average score obtained by using score when no level of completion is required. In other words, the gAvrg_100 score is assigned to missing even in those with a 0% completion (i.e., have < 20 flags). The g100_0 represents the CES-D composite score where items with ambiguous responses are assigned the gAvrg_100 value even if original within-person level of completeness is 0%. This approach is much less conservative than the previous one as the absolute eradication of missingness via a conservative group average value produces CES-D composite scores which may be said to be highly ambiguous as the large number of fabricated responses may deviate from the respondent’s unknown ‘truth’ response.
Assign “gAvrg_80” to missing if at least 80% answered (g80_80)
The CES-D composite score referred to as “g80_80” is calculated by assigning missing, don’t know, and refused answers the group average score obtained by using only those with at least a 80% non-manipulated completion. The gAvrg_80 score is only assigned to missing answers if there is at least an 80% completion (i.e., have < 4 flags). Here, items with ambiguous responses are assigned the gAvrg_80 value. The g80_80 represents the CES-D composite score where items with ambiguous responses are assigned the gAvrg_80 value where the original withinperson level of completeness was at least at 80%. The approach compromises the meaning of the CES-D composite score because the selective eradication of missingness is created via a “non-conservative group average” value—the composite score may be said to be highly ambiguous as it is difficult to determine how much made up responses deviate from the ‘truth’ answers the subject would have given.
Assign “gAvrg_80” to missing even if 0% answered (g80_0)
The CES-D composite score referred to as “g80_0” is calculated by assigning missing, don’t know, and refused answers the group average score obtained by using score when no level of completion is required. In other words, the gAvrg_80 score is assigned even in those with a 0% completion (i.e., have < 20 flags). The g80_0 represents the CES-D composite score where items with ambiguous responses are assigned the gAvrg_80 value even if original within-person level of completeness is 0%. The approach severely compromises the meaning of the CES-D composite score because the selective eradication of missingness uses a “non-conservative group average” value—producing a highly ambiguous score where many subjects are assigned responses which may significantly deviate from the ‘truth’ answers they would have given.
Assign “gAvrg_0” to missing if at least 80% answered (g0_80)
The CES-D composite score referred to as “g0_80” is calculated by assigning missing, don’t know, and refused answers the group average score obtained by using all subjects in data set as those with all missing items are assigned a zero. The gAvrg_0 score is only assigned to missing answers if there is at least a 80% completion—items with ambiguous responses are assigned the gAvrg_0 value if flags < 4. The g0_80 represents the CES-D composite score where items with ambiguous responses are assigned the gAvrg_0 value where the original withinperson level of completeness was at least at 80%. The approach notably challenges the validity and reliability of the CES-D composite score because a “radically liberal group average” value is used to eradicate a selective group of missing items. The composite score may severely affect statistical parameters and validity of inferences as the large number of fabricated answers uses a non-empirically driven value.
Assign “gAvrg_0” to missing even if 0% answered (g0_0)
The CES-D composite score referred to as “g0_0” is calculated by assigning missing, don’t know, and refused answers the group average score obtained by using the group score when no level of completion is required. In other words, the gAvrg_0 score is assigned even in those with a 0% completion—items with ambiguous responses are assigned the gAvrg_0 value where flags < 20. The g0_0 represents the CES-D composite score where items with ambiguous responses are assigned the gAvrg_0 value even if original within-person level of completeness is 0%. The approach severely challenges the validity and reliability of the CES-D composite score because a “radically liberal group average” value is used to eradicate all missing items. The composite score will probably affect statistical parameters and validity of inferences as the vast number of fabricated answers uses a non-empirically driven value.
Descriptive
The synthetic data shows from the 4,800 synthetic respondents, there are a total of 20,580 CES-D items missing: 1,980 with 0 flags (i.e., have a 100% completion); 780 with 1 flag; 180 with 4 flags; 6 flags=540 (i.e., only have a 80% level of completion); 600 with 8 flags; 240 with 10 flags; 120 with 16 flags; 240 with 18 flags; and 120 with 20 flags— this signals all items are missing. Each of the people with multiple flags must be computed. For example, the 180 with 4 flags each show that 780 CES-D items are missing (i.e., 4 × 180=780). After all multiple flags are computed in the same manner, we see from the probable 96,000 (=4,800 × 20) responses there are 20,580 missing, which equals about: (20,580÷96,000) ×100 ≈ 21%. It could be said that our synthetic data has a 21% measure of incompleteness in CES-D items. In terms of location of missingness, the sub-scale flag variables for the full sample indicate the following: on average, about 1.6 items (SD=2.21; range=0 to 7) are missing in the depressed affect CES-D sub-scale; on average, about 0.83 items (SD=1.24; range=0 to 4) are missing in the positive affect CES-D sub-scale; on average, about 1.23 items (SD=1.70; range=0 to 7) are missing in the somatic activity CES-D sub-scale; and on average, about 0.64 items (SD=0.81; range=0 to 2) are missing in the interpersonal relations CES-D sub-scale. These numbers indicate high level of missingness is most frequent in the depression affect questions than with the somatic activity items.
The values for the group average variables from the synthetic data are as follows: gAvrg_100=1.30; gAvrg_80=1.31; and gAvrg_0=1.02. As you can see, there are differences in average values when different transformation scenarios are used at the group level. Please note the values include numbers that have values in the hundredth and thousandth decimal places. The CES-D score was designed to only use whole numbers with no decimal places. There is no discussion in the literature on how decimal places should be treated. As you can see from the average variables above, the use of decimals is made—these form of single-item scores for the CES-D are likely to be produced whenever missing, illogical, or inconclusive values are replace by the average of something else. This becomes particularly important when the CES-D threshold of 16 is used to identify plausible depression and composite scores are rounded to the whole non-decimal value.
From Table 1 we see the 10 different CES-D composite scores. It could be said that CESD_100 is the only appropriate score. As you can see, only 1,980 (41%) obtain a score through non-data-editing approach. Although limiting the use of surveys that are 100% complete is desirable as no data is being arbitrarily created for the respondent, this form of approach is the most likely to create incomplete data. The presence of incomplete data renders researchers with the inability to use the complete sample in the study. This is particularly important if attempts are made to generalize from the sample to the population from which the sample was theoretically drawn from—in other words, coding CES-D only when 100% of items are complete may severely limit generalization from the sample. It could be argued that the only valid solution for handling item missingness is the production of high quality and complete data through the use of highly trained and responsible survey administrators. Anything else—despite its prevalent use and acceptability within research circles—would be the product of arbitrary decisions creating information which may deviate from the truth.
| Variable | Label | N1 | 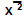 |
SD3 | Min4 | Max5 |
|---|---|---|---|---|---|---|
| No transformation on missing values6 | ||||||
| CESD_100 | Scored only if 100% of answers recorded | 1,980 | 26.1 | 19.0 | 0 | 60 |
| CESD_80 | Score if at least 80% of responses recorded | 2,940 | 27.1 | 18.5 | 0 | 60 |
| CESD_0 | Score even if 0% of responses recorded7 | 4,800 | 20.4 | 18.2 | 0 | 60 |
| Transforming missing values by assigning zeros | ||||||
| CESD_Z | Score were missing are transformed to zero | 4,800 | 22.9 | 16.9 | 0 | 60 |
| Transforming missing values by using group average from those with 100% completion | ||||||
| g100_80 | Assign gAvrg_100 if at least 80% of answers recorded | 2,940 | 27.8 | 18.8 | 0 | 60 |
| g100_0 | Assign gAvrg_100 even if 0% of answers recorded | 4,800 | 26.3 | 16.2 | 0 | 60 |
| Transforming missing values by using group average from those with at least 70% completion | ||||||
| g80_80 | Assign gAvrg_80 if at least 80% of answers recorded | 2,940 | 27.8 | 18.8 | 0 | 60 |
| g80_0 | Assign gAvrg_80 even if 0% of answers recorded | 4,800 | 26.5 | 16.2 | 0 | 60 |
| Transforming missing values by using group average that includes those with 0% completion | ||||||
| g0_80 | Assign gAvrg_0 if at least 80% of answers recorded | 2,940 | 27.7 | 18.8 | 0 | 60 |
| g0_0 | Assign gAvrg_0 even if 0% of answers recorded | 4,800 | 25.6 | 16.2 | 0 | 60 |
1Number with a score on this variable
2Mean
3Standard deviation
4Minimum
5Maximum
6Include missing, don’t know, or refused
7Those with no answers are assigned a zero for their composite score in CESD_0
Table 1: Descriptive statistics for various CES-D scores.
Compare to the 100% approach, all the other scenarios simultaneously produce more complete datasets and more ambitious CES-D composite scores—as the level of manipulation increases. If you scan the mean scores ( x ) and standard deviations (SD) from Table 1 you will be able to see that no other scoring scheme produce the same mean and SD as CESD_100. An important question arises from reviewing these numbers: Do different alteration schemes alter the mean and distribution of CES-D composite scores in samples? The synthetic data provides evidence that this question may be answered in the affirmative—which may imply that analysis of variance (is CES-D used as a continuous variable) or chi-square (if CES-D is used with threshold) result could differ under different transformation scenarios. The main argument here is that data creation protocols have the ability to affect the basic characteristics of a sample—the principle applies to the coding of any scale and even single items.
Linear regressions
The synthetic data are also used to regress on the four variables (sex, race, SES, cancer) modelling 8 CES-D composite scores. The main goal of the regressions is to show how different coding schemes can produce different results. For example, from Table 2 when the 80% level of completion threshold is used to edit CES-D data, a total of 2,940 individuals from the synthetic data are used in four equations predicting: CESD_80 were missing values are treated as zero without applying reverse coding for positive affect items only for individuals who originally answers at least 16 (i.e., 80%) of items; g100_80 were missing values are replace with the 100%-group-average when at least 80% of answers are originally given; g80_80 were missing values are replace with the 80%-group-average when at least 80% of answers are originally given; and g0_80 were missing values are replace with the 0%-groupaverage when at least 80% of answers are originally given. From Table 2, we see that using various substitutes for missing values for those with at least an 80% completion-threshold affects the independent/ exposure variables as follows: the statistically significant race-βs range from 1.88 to 2.09 (a range of 0.21); the statistically significant cancer-βs range from 5.97 to 6.08 (a range of 0.11); and the statistically significant intercept-βs range from 22.9 to 23.6 (a range of 0.7). The direction of these three βs remains the same and the small magnitude of difference is not as important as the fact that the different scenarios for handling missing data have the ability to affect point estimates.
| CESD_801 | g100_802 | g80_803 | g0_804 | |||||
|---|---|---|---|---|---|---|---|---|
| β | Pr |t| | β | Pr |t| | β | Pr |t| | β | Pr |t| | |
| Sex5 | -0.02 | 0.98 | -0.02 | 0.98 | -0.02 | 0.98 | -0.02 | 0.98 |
| Race6 | 2.09 | < 0.01 | 1.88 | < 0.01 | 1.87 | < 0.01 | 1.91 | < 0.01 |
| SES7 | 0.08 | 0.90 | 0.26 | 0.71 | 0.26 | 0.70 | 0.24 | 0.73 |
| Cancer8 | 6.08 | < 0.01 | 5.99 | < 0.01 | 5.97 | < 0.01 | 6.08 | < 0.01 |
| Model | ||||||||
| Intercept | 22.87 | < 0.01 | 23.61 | < 0.01 | 23.64 | < 0.01 | 23.45 | < 0.01 |
| Adjusted-R2 | 0.028 | < 0.01 | 0.026 | < 0.01 | 0.026 | < 0.01 | 0.027 | < 0.01 |
1Score if at least 80% of responses recorded
2Assign gAvrg_100 if at least 80% of answers recorded
3Assign gAvrg_80 if at least 80% of answers recorded
4Assign gAvrg_0 if at least 80% of answers recorded
5Male=1 and female=0;
6Racial minority=1 and racial majority=0;
7Socioeconomic status: high socioeconomic status=1 and moderate socioeconomic status=0;
8Has cancer=1 and no cancer= 0
Table 2: Linear regressions predicting CES-D with 80% completion-threshold (n=2,940).
From Table 3 when the 0% level of completion threshold is used to edit CES-D data, a total of 4,800 synthetic individuals are used in 4 equations predicting: CESD_0 were missing values are treated as zero without applying reverse coding for positive affect items for all individuals including instances when no answers were originally given; g100_0 were missing values are replace with the 100%-group-average even if no answers were originally given; g80_0 were missing values are replace with the 80%-group-average even if no answers were originally given; and g0_0 were missing values are replace with the 0%-groupaverage even if no answers were originally given. From Table 3, we see that using various substitutes for missing values for any individual including those with a 0% completion-threshold affects the predictors as follows: the statistically significant race-βs range from 1.13 to 1.72 (a range of 0.59); the statistically significant cancer-βs range from 3.72 to 5.31 (a range of 1.59); and the statistically significant intercept-βs range from 17.2 to 23.9 (a range of 6.7). The direction of these three βs remains the same in all models and magnitude is more notable than for regression results shown in Table 2 partially a product of using a different sample. The main point is that using different scenarios for replacing missing values has the ability to affect regression parameters.
| CESD_01 | g100_02 | g80_03 | g0_04 | |||||
|---|---|---|---|---|---|---|---|---|
| β | Pr |t| | β | Pr |t| | β | Pr |t| | β | Pr |t| | |
| Sex5 | -0.31 | 0.55 | -0.05 | 0.91 | -0.04 | 0.93 | -0.11 | 0.82 |
| Race6 | 1.13 | < 0.02 | 1.70 | < 0.01 | 1.72 | < 0.01 | 1.61 | < 0.01 |
| SES7 | 0.39 | 0.46 | -0.21 | 0.65 | -0.23 | 0.62 | -0.11 | 0.81 |
| Cancer8 | 5.31 | < 0.01 | 3.78 | < 0.01 | 3.72 | < 0.01 | 4.11 | < 0.01 |
| Model | ||||||||
| Intercept | 17.2 | < 0.01 | 23.7 | < 0.01 | 23.9 | < 0.01 | 22.8 | < 0.01 |
| Adjusted-R2 | 0.022 | < 0.01 | 0.016 | < 0.01 | 0.015 | < 0.01 | 0.018 | < 0.01 |
1Score even if 0% of responses recorded
2Assign gAvrg_100 even if 0% of answers recorded
3Assign gAvrg_80 even if 0% of answers recorded
4Assign gAvrg_0 even if 0% of answers recorded
5Male=1 and female=0;
6Racial minority=1 and racial majority=0;
7Socioeconomic status: high socioeconomic status=1 and moderate socioeconomic status=0;
8Has cancer=1 and no cancer= 0
Table 3: Linear regressions predicting CES-D with 0% completion-threshold (n=4,800).
The regressions show different coding schemes can affect results. With the synthetic data being used here, the differences may be considered trivial. The main point is that we do not really understand if and how much of a difference the different data editing procedures employed in the field have on regression parameters unless we begin to clearly delineate the different protocols for handling missing values. As a reminder, CES-D is not considered an inferior scale to any other scale measuring psychological, social, or physical phenomenon. The principles shown here apply to all scales and even single items which experience transformations using either implicit or explicit logic.
As the explanations of the macro above indicate, the topic is complex and requires careful attention by highly trained technicians who are equally informed by evidence from research. The topic should be expanded upon in future work by including how computer assisted program and internet surveys help with missing data. Data management that disregards the implicit assumptions being made to edit missing, inconclusive, or illogical responses may be too closely related with manipulation to be acceptable in the scientific community. Responsibility for the production of high quality data does not rest with the paraprofessional and non-academician who is charged with the production of a databank: principal and co-principal investigators must insure that transparency is provided at every step of the way. Even if leading experts in the field are consulted to develop a particular method to fix items, the decisions guiding the methodology should be made clear by divulging the descriptive statistics of flag variables.
The present study could be improved by providing a more complex macro where person- or group-average assignments are made stratified by sex, race, age, and other related factors. Future work should explore these issues as the topic of scale scoring is more broadly challenged in published work and presentations. The specific aim of this report was to highlight the logic implicit in data processing protocols that alter missing or illogical values by discussing the %CesdFlags macro. The element of clarity in data processing protocols for CES-D items applies to any survey item as every approach that fixes incomplete data makes assumptions. Obscuring, ignoring, and being silent about assumptions in data fixing make it difficult to determine the possible quantity of Type-I and Type-II errors in published research. Absolute transparency is a worthwhile goal if advancing research requires methodological precision and clarity. Mumbling scale coding methodologies in presentations or between the lines of published work slows progress by allowing the incorrect assumption that a score on a scale means the same thing across studies. Alternate scale coding algorithms should be presented and challenged in public in order to establish a standardize procedure that may allow for more inter-study comparability.
The assignment of responses through non-evidence based procedures merits careful attention as the use of CES-D continues to grow. The type of radical clarity necessary for being able to discern when regression results reflect true phenomena or are simply data artifact, requires that divulging data limitations and creation procedures no longer be associated with risking the face validity of a study. Instead, moving towards the detection of a more probable truth and distancing research from absolute uncertainty demands that ambiguous descriptions of data management be treated with suspicion. Journal editors and manuscript reviewers should continue to guard readers against those who would unintentionally produce more confusion in the field through imprecision.