Journal of Nutrition & Food Sciences
Open Access
ISSN: 2155-9600
ISSN: 2155-9600
Research Article - (2013) Volume 3, Issue 2
The distribution of usual intake of nutrients in a given population is one of the major concerns in public health nutrition, and is used to assess and prevent nutritional problems. The distribution of usual intake cannot be measured directly, but can be estimated from a dietary survey that spans multiple days. The prevalence of nutritionally high-risk people, defined as the proportion of a population that does not achieve the dietary reference intake, can be estimated from the distribution of usual intake in the population. Although several methods have been proposed, there is no universally accepted method for estimating the distribution and prevalence of nutritionally high-risk people. In this study, we improved an existing method and used simulation studies to compare the performance of the new method, with that of 2 previously proposed methods. Our proposed method outperformed them, particularly in a realistic situation, and with a small sample size, providing a more accurate and precise estimate of the prevalence of nutritionally high-risk people.
Keywords: Dietary survey; Dietary reference intakes; Usual intake; Dietary assessment; Nutrients; Nutritional epidemiology; Statistical method; Sodium intake; Prevalence of nutritionally high-risk people; ISU (Iowa State University) method
DRI: Dietary Reference Intake; EAR: Estimated Average Requirement; DG: Dietary Goal; ISU: Iowa State University; RMSE: Root Mean Square Error
The nutritional status of a population is often evaluated by determining the proportion whose usual intake of nutrients falls short of, or exceeds reference values. For instance, dietary reference intakes (DRIs) are reference values for the amount of each nutrient required to maintain good health [1,2]. These reference values have been established not only to prevent nutrient deficiency, but also to prevent lifestyle-related diseases attributable to inappropriate nutrient intake [3]. The estimated average requirement (EAR), one of the DRIs, is the estimated amount needed to satisfy the nutritional requirements of half the people in a certain group, and is defined through review of the scientific literature [4,5]. The tentative dietary goal for preventing lifestyle-related diseases (DG), a DRI unique to Japan, has been established to reduce the risks for selected lifestyle-related diseases such as cardiovascular disease and hypertension [1]. EAR shave been utilized in dietary assessments of protein, iron, vitamin B1 and other nutrients [1,2]. DGs have been utilized in dietary assessment of sodium (salt), dietary fiber, saturated fatty acid, potassium and other nutrients [1]. Nutritionally high-risk individuals are those who do not achieve the DRIs: the proportion of such individuals in the population provides a measure of nutritionally high-risk prevalence.
To assess the diet of a population, a dietary survey is conducted, and the distribution of daily intake of a nutrient is measured. Usual intake is defined as the long-run average of daily intakes of a dietary component by an individual. From the viewpoint of public health nutrition, information on the usual intake distribution of a population is necessary, but this is estimated because the distribution of usual intake is not measured [6]. Biases exist in the measured daily intake distributions obtained from single-day dietary surveys due to withinsubject (day-to-day) variation; therefore, multiple-day dietary surveys are required to estimate the usual intake distribution [7,8]. Several methods have been proposed to estimate the usual intake distribution of a given population. The National Research Council proposed the first statistical method to address this issue [9]. Nusser et al. [10] proposed a semi-parametric model, and developed software that is commonly used to accomplish this estimation [10,11]; their model is known as the Iowa State University (ISU) method.
Although both methods are available to dietitians, one problem still remains. It is often the case that the usual intake distribution needs to be estimated for subgroups such as sex and age groups [12-15]. The 2 existing methodologies are not suitable for such analysis, because of the small sample size of each subgroup. Waijers et al. [16,17] proposed another parametric model based on a mixed-effect model, AGE MODE, to resolve this issue. The AGE MODE model assumes that the mean structure of usual intake varies depending on the subject’s age. AGE MODE is useful when the usual intake of a nutrient is justifiably assumed to vary with age. However, AGE MODE assumes a constant between-subject variance and a constant within-subject variance of nutritional intakes for different ages: this is problematic, because this assumption is not always correct. Data from the annual report of the National Health and Nutrition Survey in Japan [12,18] have indicated that the variance of nutritional intake does not remain static, but varies according to age.
We developed a statistical model, AGEVAR MODE, to enable nutritional intake modeling that fits better with actual data. Our current aim was to examine and compare the performance of the ISU method, AGE MODE and AGEVAR MODE through simulation studies. Thereafter, we analyzed actual dietary survey data using the 3 methods, and estimated the prevalence of nutritionally high-risk people.
AGEVAR MODE, the proposed method
For a nutrient, some form of distribution is expected for the usual intakes between subjects and the daily intake data. In the proposed AGEVAR MODE model, age explains a subject’s usual intake betweensubject variance (inter-individual variance), and within-subject variance (intra-individual or day-to-day variance). AGEVAR MODE modeling is performed in 3 steps. In Step1, the multiple-day intake data are transformed by Box-Cox transformation to an almost normal distribution [19]. In Step 2, the individual mean structure of usual intake is estimated as an optimal fraction polynomial of age in the transformed data. This procedure of estimating the mean structure of usual intake distribution is the same as that of AGE MODE. In AGEVAR MODE, monotonic exponential functions of age are simultaneously fitted to between-subject variance and within-subject variance separately. These procedures lead to an estimated usual intake normal distribution with between-subject variance for each age. The usual intakes of subjects at each age are supposed to be distributed in this usual intake distribution in the transformed scale. The daily intakes of each subject are expected to be normally distributed with the subject’s mean usual intake, and the within-subject variance of each age in the transformed scale. In Step 3, the estimated mean and between-subject variances of usual intake distribution are compared with the bias-corrected DRI in the transformed scale at each age, and the prevalence of nutritionally highrisk people at each age is estimated. The average prevalence, weighted by the number of subjects at each age, is the prevalence of nutritionally high-risk people in a given group. In Step 4, the estimated usual intake distribution in the nutrient’s original scale is obtained by the inverse function of Box-Cox transformation, correcting the bias caused by within-subject variance [20].
Step 1: Box-cox transformation: With the optimal λ of generally right-skewed intake data, Box-Cox transformation, g(.), produces almost normally distributed, symmetrical data [19]. Let yij be the measured single-day intake data of subject i on day j. Box-Cox transformation of the right-skewed histogram of yij is
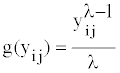 (1)
(1)
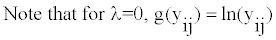 (2)
(2)
To seek the optimal λ, we use grid searching for the profile likelihood. Any optimization method could be used for this optimization in AGEVAR MODE.
Step 2: Fitting a fractional polynomial to the transformed data: The fractional polynomial for the mean structure at each age is
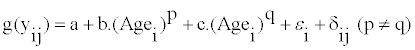 (3)
(3)
Or
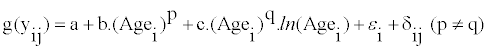 (4)
(4)
Where the between-subject variationεi is normally distributed with variance 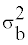 and the within-subject variation, δij is normally distributed, with variance
and the within-subject variation, δij is normally distributed, with variance 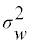 in the transformed scale:
in the transformed scale: 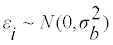
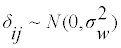
Agei is the age of subject i, and g(yij) is the Box-Cox transformed intake. p and q can take the value of [-2, -1, -0.5, 0, 0.5,1,2].
AGEVAR MODE regresses the between-subject variance 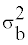 and within-subject variance
and within-subject variance 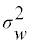 on age, simultaneously:
on age, simultaneously:
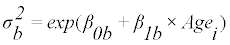 (5)
(5)
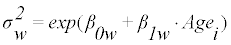 (6)
(6)
The model of (Equation 3) or (Equation 4) is selected, and the parameters a, b, c, p, q, β0b, β0b, β0b, β1b, β0w, and β1w are determined, so that they maximize the likelihood of the model (optimization). The estimated parameters determine the distribution of usual intake, g(yi), at each age in the transformed scale. The estimated usual intake distribution in the transformed scale at each age is
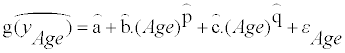 (7)
(7)
where
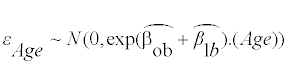
or
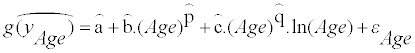 (8)
(8)
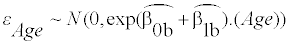 . The optimal distribution of the two for the likelihood is selected.
. The optimal distribution of the two for the likelihood is selected.
Step 3: Estimating the prevalence of nutritionally high-risk people: To estimate the prevalence of nutritionally high-risk people in any group, a straightforward approach would be to compare the back-transformed distribution 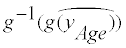 (9), with the DRI value in the nutrient’s original scale. However, we have provided an alternative means of using the feature of normal distribution function in the transformed scale, since the estimated usual intake distribution in the nutrient’s original scale is right-skewed, and the straightforward method would require numerous calculations of a Monte Carlo algorithm [16]. In general, when a daily intake normal distribution of a given subject with the subject’s mean and a within-subject variance in the transformed scale is back-transformed by a non-linear function, the value of the back-transformed subject’s mean is biased from the arithmetic mean of the back-transformed distribution [20]. For this reason, Box-Cox transformation or back-transformation, which are non-linear functions, requires bias correction; bias is caused by withinsubject variance in each subject at each age. Using the Newton-Raphson method [21,22], we numerically solve the bias-corrected DRI value in the transformed scale at each age, which corresponds to the DRI value in the nutrient’s original scale, when back-transformed with Equation 9. The previous AGE MODE method solves this requirement for bias correction, by generating a right-skewed Monte Carlo distribution of each subject in the nutrient’s original scale [16]. Comparing the normal cumulative distribution function with the bias-corrected DRI in the transformed scale, we calculate the prevalence of nutritionally high-risk people at each age. The prevalence of nutritionally high-risk people in any group is then estimated as the weighted average of the age-specific prevalence, where the weight is the number of subjects at each age.
(9), with the DRI value in the nutrient’s original scale. However, we have provided an alternative means of using the feature of normal distribution function in the transformed scale, since the estimated usual intake distribution in the nutrient’s original scale is right-skewed, and the straightforward method would require numerous calculations of a Monte Carlo algorithm [16]. In general, when a daily intake normal distribution of a given subject with the subject’s mean and a within-subject variance in the transformed scale is back-transformed by a non-linear function, the value of the back-transformed subject’s mean is biased from the arithmetic mean of the back-transformed distribution [20]. For this reason, Box-Cox transformation or back-transformation, which are non-linear functions, requires bias correction; bias is caused by withinsubject variance in each subject at each age. Using the Newton-Raphson method [21,22], we numerically solve the bias-corrected DRI value in the transformed scale at each age, which corresponds to the DRI value in the nutrient’s original scale, when back-transformed with Equation 9. The previous AGE MODE method solves this requirement for bias correction, by generating a right-skewed Monte Carlo distribution of each subject in the nutrient’s original scale [16]. Comparing the normal cumulative distribution function with the bias-corrected DRI in the transformed scale, we calculate the prevalence of nutritionally high-risk people at each age. The prevalence of nutritionally high-risk people in any group is then estimated as the weighted average of the age-specific prevalence, where the weight is the number of subjects at each age.
Step 4: Estimating the usual intake distribution of a population in the original scale of the nutrient: Simple 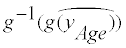 in the nutrient’s original scale is biased by within-subject variance. Using the Delta-method [20-23], the estimated usual intake right-skewed distribution in the nutrient’s original scale is
in the nutrient’s original scale is biased by within-subject variance. Using the Delta-method [20-23], the estimated usual intake right-skewed distribution in the nutrient’s original scale is
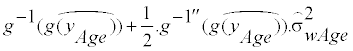 (10)
(10)
g−1"(.) is the second order differential of g−1 (.) , and
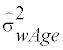 is the estimated within-subject variance at each age in the transformed scale. The estimated usual intake distribution of any group in the nutrient’s original scale is obtained by summing Equation 10.
is the estimated within-subject variance at each age in the transformed scale. The estimated usual intake distribution of any group in the nutrient’s original scale is obtained by summing Equation 10.
Simulation study
To compare the performance of the ISU method, AGE MODE and our proposed AGEVAR MODE, we conducted simulation studies on 4 scenarios mimicking actual data for sodium intake in women. In nutritional surveys, within-subject variance is generally larger than between-subject variance. Between-subject variance increases with age, while within-subject variance decreases with age [12]. This is especially true for sodium intake; elderly Japanese people generally consume traditional Japanese salty food.
In our actual intake survey data, the optimal λ of Box-Cox transformation was estimated as -0.05 for sodium intake in women. The female DG for usual intake of salt is less than 7.5 g [24]. This amount of salt (7.5 g) corresponds to 2949 mg sodium in the original scale of sodium, and 6.59 in the Box-Cox transformed scale, after Box-Cox transformation with λ=-0.05. Hereafter, we refer to the salt DRI for women as 2949 mg sodium.
The simulations were based on the 4 scenarios below. The total number of female subjects in the scenarios for one data set was set at 1500, a number similar to the sample size of a dietary survey conducted by a local government in Japan [13-15,25,26]. The number at each age was proportional to that of the Japanese population in 2010, based on national census data [27]. The settings for the 4 simulation study scenarios in the transformed scale are presented in table 1, and graphs of the 4 simulation scenarios in the original scale of the nutrient (sodium) are depicted in figure 1. The data for scenario (4) were intended to be similar to our actual data. In the other scenarios, either the mean and variance, or both in scenario (4) were set as constants. For each scenario, we generated 3 days of sodium intake data for 1500 subjects, and analyzed the data set derived from the ISU method, AGEMODE, and AGEVAR MODE. We repeated this procedure 10,000 times separately. The settings for all 4 scenarios described below are in the transformed scale.
| Mean | Between-subject variance | Within-subject variance | |
|---|---|---|---|
| Scenario (1) | Constant (6.8) | Constant (0.03) | Constant (0.06) |
| Scenario (2) | Constant (6.8) | Increases linearly according to age (0.04-0.06 as age increases from 18 to 79 years) | Decreases linearly according to age (0.07-0.05 as age increases from 18 to 79 years) |
| Scenario (3) | Increases linearly according to age (6.6-7.0 as age increases from 18 to 79 years) | Constant (0.03) | Constant (0.06) |
| Scenario (4) | Increases linearly according to age (6.6-7.0 as age increases from 18 to 79 years) | Increases linearly according to age (0.04-0.06 as age increases from 18 to 79 years) | Decreases linearly according to age (0.07-0.05 as age increases from 18 to 79 years) |
Table 1: Settings for the 4 simulation studies. Intake amounts are set in the transformed scale.
Figure 1: Graphs of the settings of the 4 scenarios for simulation studies in the nutrient’s original scale. Amounts of sodium and salt in the original scale: Y-axis (left), sodium; Y-axis (right), salt. *between SD=between-subject standard deviation. †Salt dietary reference intake in women; 7.5 g salt is equivalent to 2949 mg sodium.
The performance of each of the 3 methods was evaluated with 3 statistical indexes: bias, standard error, and root mean square error (RMSE) of estimated prevalence of nutritionally high-risk people. These indexes were calculated with 10,000 estimates of the prevalence of nutritionally high-risk people by the 3 methods. RMSE was the primary performance index in this study because it accounts for bias and standard error.
Scenario (1): Constant mean and constant variance in the transformed scale through the age range: The constant mean of usual intake through the age range is 6.8. The constant between-subject variance is 0.03, i.e. the constant between-subject standard deviation is 0.17. The constant within-subject variance is 0.06, i.e. the constant within-subject standard deviation is 0.24.
Scenario (2): Constant mean and linear variance in the transformed scale through the age range: The constant mean of usual intake through the age range is 6.8. The between-subject variance is described as follows: 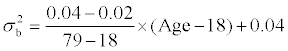 the betweensubject variance changes linearly from 0.02 to 0.04 as age increases from 18 to 79 years, i.e. the between-subject standard deviation changes from 0.14 to 0.2. The within-subject variance is described as follows:
the betweensubject variance changes linearly from 0.02 to 0.04 as age increases from 18 to 79 years, i.e. the between-subject standard deviation changes from 0.14 to 0.2. The within-subject variance is described as follows: 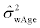 the within-subject variance changes linearly from 0.07 to 0.05 as age increases from 18 to 79 years, i.e. the within-subject standard deviation changes from 0.26 to 0.22.
the within-subject variance changes linearly from 0.07 to 0.05 as age increases from 18 to 79 years, i.e. the within-subject standard deviation changes from 0.26 to 0.22.
Scenario (3): Linear mean and constant variance in the mean and constant variance in the transformed scale through the age range: The mean of usual intake through the age range equals 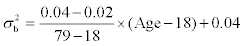 .The mean changes linearly from 6.6 to 7.0, as age increases from 18 to 79 years. The constant between-subject variance through the age range is 0.03, i.e. the constant between-subject standard deviation is 0.17. The constant within-subject variance is 0.06, i.e. the constant within-subject standard deviation is 0.24.
.The mean changes linearly from 6.6 to 7.0, as age increases from 18 to 79 years. The constant between-subject variance through the age range is 0.03, i.e. the constant between-subject standard deviation is 0.17. The constant within-subject variance is 0.06, i.e. the constant within-subject standard deviation is 0.24.
Scenario (4): Linear mean and linear variance in the transformed scale through the age range: The mean of usual intake through the age range equals 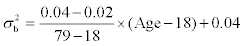 the mean changes linearly from 6.6 to 7.0 as age increases from 18 to 79 years. The between-subject variance equals
the mean changes linearly from 6.6 to 7.0 as age increases from 18 to 79 years. The between-subject variance equals 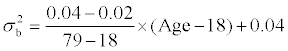 ; the between-subject variance changes linearly from 0.02 to 0.04, as age increases from 18 to 79 years, i.e. the between-subject standard deviation changes from 0.14 to 0.2. The within-subject variance equals
; the between-subject variance changes linearly from 0.02 to 0.04, as age increases from 18 to 79 years, i.e. the between-subject standard deviation changes from 0.14 to 0.2. The within-subject variance equals  the within-subject variance changes linearly from 0.07 to 0.05, as age increases from 18 to 79 years, i.e. the within-subject standard deviation changes from 0.26 to 0.22.
the within-subject variance changes linearly from 0.07 to 0.05, as age increases from 18 to 79 years, i.e. the within-subject standard deviation changes from 0.26 to 0.22.
An example of applying AGEVAR MODE to estimate usual intake distribution of sodium in women
The ISU method, AGEMODE, and AGEVAR MODE were applied to the sodium data of Japanese women from a 12-day survey, and the prevalence of nutritionally high-risk people was estimated for each age group and for the overall group.
In these data, the subjects were volunteers who participated in a dietary survey conducted in 2004 and 2005, and who lived in Aomori, Akita, Iwate, Yamagata, Nagano, Gunma, Chiba, Okayama, Tokushima, Kochi, Fukuoka, or Miyazaki Prefecture in Japan. The subjects were aged 18-79 years; there were 208 men and 257 women. The survey was carried out through 4 seasons: in May and June (spring), August and September (summer), November and December (autumn), and February and March (winter). During each season, the survey was conducted on 3 non-consecutive days; 2 of which were weekdays and one of which was a weekend day. The interval between the first and the third day was less than 2 weeks during each season [28]. The ethics committee of the National Institute of Health and Nutrition in Japan approved this survey. All participants provided written consent for collaboration. Nutrient daily intakes were measured as they were for the Japan National Health and Nutrition Survey, where by each household kept a 1-day diet record of the intake of each person. Dietitians queried the families, when collecting the surveys to confirm the accuracy of the information provided. Nutritional intakes were calculated using the Fifth Revision of the Standard Food Composition Table [29].
All analyses and simulation studies were performed using SAS v9.3 (Cary, NC, USA). The ISU estimating method was carried out using Side Program written in SAS [11].
The simulation study results for the 4 scenarios are presented in table 2.
| Age, years (No. of subjects) | True prevalence (%) | Performance in estimating the prevalence of nutritionally high-risk people† | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias (%) | Standard error (%) | RMSEc(%) | |||||||||||
| ISU | AGE | AGEVAR | ISU | AGE | AGEVAR | ISU | AGE | AGEVAR | |||||
| Scenario 1 | 18–29 (239) | 92.0 | -0.1 | -0.0 | -0.0 | 2.6 | 1.4 | 1.7 | 2.6 | 1.4 | 1.7 | ||
| 30–49 (520) | 92.0 | -0.0 | +0.0 | +0.1 | 1.7 | 1.0 | 1.1 | 1.7 | 1.0 | 1.1 | |||
| 50–69 (527) | 92.0 | -0.0 | +0.0 | +0.0 | 1.6 | 1.0 | 1.0 | 1.6 | 1.0 | 1.0 | |||
| 70–79 (214) | 92.0 | -0.1 | -0.0 | -0.0 | 2.5 | 1.4 | 1.7 | 2.6 | 1.4 | 1.7 | |||
| Total (1500) | 92.0 | -0.0 | +0.0 | +0.0 | 1.0 | 0.9 | 0.9 | 1.0 | 0.9 | 0.9 | |||
| Scenario 2 | 18–29 (239) | 88.9 | +0.2 | -2.7 | +0.1 | 2.8 | 1.7 | 1.9 | 2.9 | 3.2 | 1.9 | ||
| 30–49 (520) | 87.2 | +0.3 | -1.0 | +0.6 | 1.8 | 1.1 | 1.2 | 1.8 | 1.5 | 1.3 | |||
| 50–69 (527) | 85.1 | +0.2 | +1.1 | +1.1 | 1.8 | 1.1 | 1.2 | 1.8 | 1.6 | 1.6 | |||
| 70–79 (214) | 83.7 | +0.3 | +2.5 | +1.3 | 2.8 | 1.8 | 2.0 | 2.9 | 3.1 | 2.4 | |||
| Total (1500) | 86.2 | +0.2 | -0.0 | +0.8 | 1.1 | 1.0 | 1.0 | 1.1 | 1.0 | 1.3 | |||
| Scenario 3 | 18–29 (239) | 68.0 | +0.4 | +0.0 | + 0.1 | 4.7 | 3.0 | 3.1 | 4.7 | 3.0 | 3.1 | ||
| 30–49 (520) | 85.0 | +0.2 | -0.0 | -0.0 | 2.2 | 1.3 | 1.4 | 2.2 | 1.3 | 1.4 | |||
| 50–69 (527) | 96.4 | +0.0 | +0.1 | +0.1 | 1.0 | 0.6 | 0.6 | 1.0 | 0.6 | 0.6 | |||
| 70–79 (214) | 99.2 | -0.1 | -0.0 | -0.1 | 0.6 | 0.3 | 0.4 | 0.6 | 0.3 | 0.4 | |||
| Total (1500) | 88.3 | +0.3 | +0.0 | +0.0 | 1.0 | 0.9 | 1.0 | 1.1 | 0.9 | 1.0 | |||
| Scenario 4 | 18–29 (239) | 66.4 | +0.8 | -2.2 | +0.3 | 4.4 | 2.7 | 3.0 | 4.4 | 3.5 | 3.0 | ||
| 30–49 (520) | 80.1 | +0.5 | -1.1 | +0.7 | 2.2 | 1.4 | 1.4 | 2.2 | 1.7 | 1.6 | |||
| 50–69 (527) | 91.1 | +0.2 | +0.9 | +0.8 | 1.4 | 0.8 | 0.9 | 1.4 | 1.2 | 1.2 | |||
| 70–79 (214) | 95.5 | -0.0 | +1.3 | +0.9 | 1.4 | 0.6 | 0.9 | 1.4 | 1.4 | 1.0 | |||
| Total (1500) | 84.0 | +0.2 | -0.2 | +0.6 | 1.1 | 0.9 | 1.0 | 1.1 | 1.0 | 1.2 | |||
aIowa State University; bDietary reference intake; cRoot mean square error.
†Nutritionally high-risk=Usual intakeof sodium ≥ 2949 mg.
Table 2: Performance of the ISUa method, AGE MODE, and AGEVAR MODE in the 4 simulation studies.Female DRIb for sodium<2949mg†.
Scenario (1): The 3 methods resulted in almost null biases. Standard errors and RMSEs were smaller with AGE MODE and AGEVAR MODE, than with the ISU method.
Scenario (2): Of the 3 methods compared, the biases were smallest with the ISU method. Biases changed in a single direction with age with AGE MODE and AGEVAR MODE. The biases with the ISU method and AGEVAR MODE were acceptable, while those with AGE MODE were unacceptably high. Standard errors with AGE MODE and AGEVAR MODE were smaller than those with the ISU method were. Thus, the RMSE with AGEVAR MODE was the smallest for each age group.
Scenario (3): AGE MODE and AGEVAR MODE resulted in almost null biases, while the ISU method led to single-direction bias with age. The standard error in each age group was smaller with AGE MODE and AGEVAR MODE, than with the ISU method. This led to a superior RMSE performance with AGE MODE and AGEVAR MODE, in comparison with the ISU method.
Scenario (4): Although biases were smallest with the ISU method, higher with AGEVAR MODE, and higher still with AGE MODE, overall the ISU method yielded an exceptionally high standard error in each age group, compared with the other methods. Consequently, AGEVAR MODE was considered superior to the other methods for RMSE in each age group.
Example: The prevalence of nutritionally high-risk people varied when estimated by the 3 different methods (Table 3). The prevalence of nutritionally high-risk people across the overall group was 94.6%, 92.0%, and 93.5% with the ISU method, AGE MODE, and AGEVAR MODE, respectively. The true prevalence of nutritionally high-risk people was unknown, because we used actual data. With AGE MODE and AGEVAR MODE, the estimated prevalence increased with age. With the ISU method, the prevalence did not always increase with age.
| Age, years (No. of subjects) | Estimation for prevalence of nutritionally high-risk people† | |||
|---|---|---|---|---|
| ISU | AGE | AGEVAR | ||
| Analysis of actual 12-day survey data | 18–29 (42) | 85.2 | 79.8 | 84.4 |
| 30–49 (56) | 94.5 | 91.9 | 92.9 | |
| 50–69 (136) | 97.0 | 97.0 | 96.7 | |
| 70–79 (23) | 96.8 | 98.4 | 96.9 | |
| Total (257) | 94.6 | 92.7 | 93.5 | |
aIowa State University.
†Nutritionally high-risk=Usual intakeof sodium ≥ 2949 mg.
Table 3: An example of the estimated prevalence of nutritionally high-risk people† by the ISUa method, AGE MODE, and AGEVAR MODE.
We built a mixed-effect model with changing variance, called AGEVAR MODE. As expected, AGEVAR MODE performed well in a realistic scenario (4) involving small sample subgroups. AGE MODE performed best in scenarios (1) and (3), where the mean structure of the usual intake distribution changed linearly and had the smallest standard errors, as expected, though AGEVAR MODE also had relatively small standard errors. Overall, the ISU method had the smallest biases in all scenarios, indicating that ISU method might be the best available for larger sample sizes. In scenario (2), where only variance changed with age, standard errors were slightly larger with AGEVAR MODE, than with AGE MODE. However, AGEVAR MODE had smaller biases in estimation of the prevalence of nutritionally high-risk people than AGE MODE.
Figure 2 shows that the results of analysis with AGEVAR MODE for the actual data were similar to the settings of scenario (4). Taking into account the results of scenario (4) in the simulation study (Table 2), the estimates of the prevalence of nutritionally high-risk people (Table 3) might be positively biased to some extent with the ISU method and AGEVAR MODE; the range of true prevalence of nutritionally highrisk people may not be as wide as the prevalence estimated by the 3 methods in table 3.
Figure 2: The result of AGEVAR MODE analysis for actual data of salt intake in women. Amounts of sodium and salt in the original scale: Y-axis (left), sodium; Y-axis (right), salt. *between SD=between-subject standard deviation. †Salt dietary reference intake in women; 7.5 g salt is equivalent to 2949 mg sodium.
There is a great need for accurate estimation of the usual intake distributions of nutrients and the prevalence of nutritionally high-risk people in a given population, especially based on small sample surveys. For example, a dietary survey is conducted in each prefecture in Japan every 3-5years, to assess the progress of the local health promotion plan called Health Japan 21 [30]. Recently, small 2-day dietary surveys were conducted: the Saitama Prefectural Health and Nutrition Survey (n=1351), the Nagano Prefectural Health and Nutrition Survey (n=1244), and the Kumamoto Prefectural Health and Nutrition Survey (n=1195). From these surveys, the distributions of usual intake and the prevalence of nutritionally high-risk people for energy intake and each nutrient were estimated according to sex and age groups [7,8,13,25,26], using the ISU method [10,11]. Unfortunately, the ISU method is limited by large standard errors, when used to analyze small sample sizes, such as those for age-specific analysis. AGEVAR MODE would be more useful for small samples because of its smaller bias and lower standard errors.
Our study has some limitations. First, AGEVAR MODE assumes a monotonic change in both between-subject and within-subject variances, and does not deal with U- or J-shaped age variances. Therefore, AGEVAR MODE may not fit such data. However, such a situation is not likely to occur in actual situations, because dietary culture is passed from one generation to another. Second, we fitted 3 models to simulation data and actual data for sodium intake in women. To better assess the performance of the 3 methods, data for other nutrients need to be fitted and analyzed. Third, these 3 methods do not assume frequent zero intakes, even though the intake of foods such as bacon, cheese, and tomatoes can be zero on any given day. However, the intakes of nutrients such as sodium, fat, and protein in a day cannot be zero. Overall, we consider these 3 methods all now available for use in the analysis of nutrient intake.
Our improved method to estimate the usual intake distribution and the prevalence of nutritionally high-risk people showed good performance, when compared with the 2 existing modeling methods. This method will help promote the use of DRIs; help improve our understanding of the nutritional status among populations, and aid in confronting the challenges of public health nutrition.
The survey in this study was funded by project and research grants from the Ministry of Health, Labour and Welfare, Japan. The authors are grateful to the local healthcare staff in across Japan, especially the dieticians for collecting the dietary intake data.