Journal of Theoretical & Computational Science
Open Access
ISSN: 2376-130X
ISSN: 2376-130X
Research Article - (2015) Volume 2, Issue 1
Rapid and accurate solutions for nonlinear ordinary differential equations (ODEs) that arise in the pharmaceutical sciences are desirable. This is particularly important in the area of pharmacokinetic-pharmacodynamics modelling and design. We describe an iterative linearization to generate inductive approximations which converge to the solution. These approximations allow quick and accurate evaluations of the pharmacokinetic-pharmacodynamic PKPD models. The inductive approximations are applied to a simple nonlinear pharmacokinetic (PK) model, ie a model that is nonlinear when expressed as an ordinary differential equation, and show the utility of the method. Because the approximations depend continuously on the parameters and time, the inductive method is particularly suitable for parameter estimation and optimal design approaches.
<Keywords: PKPD; Nonlinear ordinary differential equations; Analytical approximations; Optimal design; Parameter estimation
Understanding the time course and extent of drug effects is important in order to determine the best dose and dosing regimen to meet the needs of both clinical use and drug development [1]. Pharmacokinetic-pharmacodynamic (PKPD) models are used to describe the time course of drug effects and the study of these processes has been the subject of considerable attention. Pharmacokinetics (PK) defines models used to describe the change in concentrations of the drug in the body over time and pharmacodynamics describes the relationship between concentration and effect. The combination of PK and PD (to give PKPD) therefore links drug effects to time. Recently the European Medicines Agency has instigated a working party to promote integration of PKPD modelling and simulation processes into drug development (see recent opinion piece [2]). Due to nonlinearities in the structure of PKPD models, it is common that PKPD models are expressed as ordinary differential equations. In addition, these models are generally cast in a population framework with random effects on the parameter and data levels. This leads to high dimensionality and when combined with time-stepping solvers for ordinary differential equations (ODEs) (e.g. algorithms based on the Runge Kutta technique) can be computationally intensive with many function calls required for estimation, optimisation (such as optimal design [3]) or simulation [4] processes. Rapid and accurate solutions for nonlinear differential equations would provide a valuable asset to those development and application of PKPD models.
Here we consider how to solve systems of first-order nonlinear ODEs. These have the general form:
 (1)
(1)
where t is time, 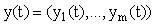 is a m x 1 vector of response variables (i.e. concentrations and/or effects), and where
is a m x 1 vector of response variables (i.e. concentrations and/or effects), and where 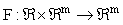 is a nonlinear function of y. Unfortunately, exact closed form solutions to such systems are only available in (relatively) few cases; for example, the Michaelis-Menten system for a zero order input where the exact solution may be written in terms of the Lambert-W function [5]. However, even if the solution cannot be written in closed form, there are many methods (both numerical and analytical) for generating approximate solutions which share many desirable characteristics with the exact solution and which are accurate to any order (see for example [6] for some introductory comments).
is a nonlinear function of y. Unfortunately, exact closed form solutions to such systems are only available in (relatively) few cases; for example, the Michaelis-Menten system for a zero order input where the exact solution may be written in terms of the Lambert-W function [5]. However, even if the solution cannot be written in closed form, there are many methods (both numerical and analytical) for generating approximate solutions which share many desirable characteristics with the exact solution and which are accurate to any order (see for example [6] for some introductory comments).
In this work we introduce an inductive method of generating approximate solutions to nonlinear systems based on an iterative linearization. We explore this method using a simple example that has no known closed form solution. Our intention is to provide a example, which in this case is given by a one-compartment first-order input Michaelis-Menten output model, for which no analytical solution exists and hence from which the methods we propose can be described as simply as possible. The proposed iterative linearization method has wide applicability to other nonlinear models, e.g. recursive systems such as the coagulation network [7] and more complicated systems of differential equations that contain Michaelis-Menten.
Theory
The first-order nonlinear systems (1) may be rewritten in the form:
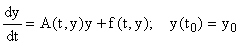 (2)
(2)
where A(t, y) is an m × m non-singular matrix, y(t) and f(t,y) are column vectors, and 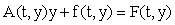 There are usually several different ways of writing (1) in this form, starting with the simple setting where A = 0 and f = F. Here we wish to focus on decompositions which reflect the linearization of the equation, i.e.
There are usually several different ways of writing (1) in this form, starting with the simple setting where A = 0 and f = F. Here we wish to focus on decompositions which reflect the linearization of the equation, i.e. 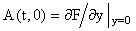 Starting with an (arbitrary) initial approximation
Starting with an (arbitrary) initial approximation 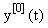 , we may inductively define a sequence of approximations
, we may inductively define a sequence of approximations 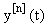 as solutions now represented in a first-order linear system:
as solutions now represented in a first-order linear system:
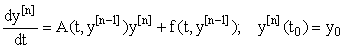 (3)
(3)
We see that A and f now depend on the previous iteration 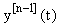 ,which is a known quantity, rather than on the current value of y(t), and hence the nonlinearity is avoided. Since (3) is a first-order linear system, we can then apply the integrating factor formula given in Appendix B to write the solution as:
,which is a known quantity, rather than on the current value of y(t), and hence the nonlinearity is avoided. Since (3) is a first-order linear system, we can then apply the integrating factor formula given in Appendix B to write the solution as:
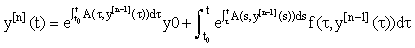 (4)
(4)
Even if each integral cannot be solved algebraically, each of the integrals in this formula may be quickly and accurately estimated using Gaussian quadrature.
Application
Here we apply the inductive method described above to a nonlinear system that describes the concentration of a drug with first-order input and Michaelis-Menten output, i.e.
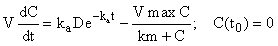 (5)
(5)
where C(t0) is the initial concentration of drug in the blood (at time zero) with units of mg/L, D is dose (1 mg) and the parameters, ka (first-order absorption rate constant), Vmax (maximum velocity of the enzyme) and km (Michaelis-Menten constant – defined as the concentration for which the enzyme is at half-maximal rate). The parameters and their values are given in (Table 1).
| Parameter | Description | Value, units |
|---|---|---|
| Vmax | Maximum elimination rate | 0.0734 mg/h |
| km | Michaelis-Menten constant | 0.3672 mg/L |
| V | Volume of distribution | 1 L |
| ka | Absorption rate constant | /h |
Table 1: Parameters and their values for system (equation 5).
This system can obviously be written in the form (eqn 2) by letting y(t) = C(t) and
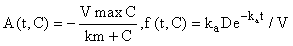
and hence, according to the inductive scheme above and starting with the naive initial estimate 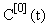 (for all t), we can now generate successive approximations inductively which converge to the solution of (equation 5), i.e.
(for all t), we can now generate successive approximations inductively which converge to the solution of (equation 5), i.e.
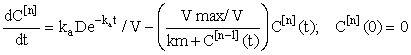 (6)
(6)
For n = 1, 2, 3, .... Using the integrating factor formula in (eqn 4), we get the solution for the nth iterate expressed in integral form:
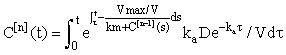 (7)
(7)
We see that for n = 1 this can be evaluated exactly to give the linear approximation, i.e.
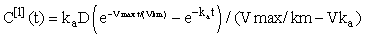
Subsequent iterates can be estimated using Gauss-Legendre quadrature, i.e.
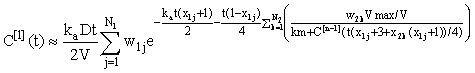
where χij, wij are Ni- point abscissas and weights for i = 1, 2 (these can be calculated using the method given in Trefethen [8]).
The convergence of the inductive estimates C[n](t) can be seen in (Figure 1) (using N1 = N2 = 5 in the Gaussian quadratures). The choice of 5 iterations is arbitrary and can be chosen to suit the accuracy requirements of the particular use of the model. The lower dashed line represents the linear approximationC[1](t) . It is seen that as number of iterations increase the inductive approximations approach the solution provided by the ODE45 solver in MATLAB(MATrix LABoratories R2014a,The Math Works Inc). ODE45 is a medium order non-stiff differential equation solver that is based on the 4th order Runge-Kutta solution. We show this figure to provide a sense of the relative accuracy of the method as the number of iterations increases. In this setting the time-stepping ODE solution is in itself not accurate and hence is only providing a benchmark for the approach. A more rigorous approach to considering accuracy is shown in (Figure 2). Here we see that the relative error between successive approximations 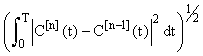 appears to be decaying exponentially as a function of n. This is significant because it means that the series:
appears to be decaying exponentially as a function of n. This is significant because it means that the series:
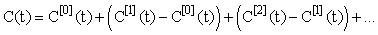
Will be absolutely convergent and hence the inductive approximation will approach the true (but unknown) solution. The accuracy of the inductive linearization can therefore be determined to any arbitrary level of accuracy. The choice used for the initial estimate C[0](t) = 0 works well when the input coefficient ka D is small in comparison to the output coefficient Vmax/km (so that C(t) <
Here we see how the solution to any system of first-order nonlinear ODEs can be approximated by a sequence of inductive approximations which are generated as solutions for first-order linear equations. This is a versatile and powerful technique of generating analytical approximations which are accurate across a broad range of times and parameter values. This means that the inductive method is particularly suitable for applications in optimal design and parameter estimation when the structural model is expressed in terms of nonlinear differential equations. We have attempted to keep the work here as simple as possible and apply the method to a simple set of differential equations, which we have written as a single differential equation. However the method can be used to solve larger sets of differential equations, including recursive systems, such as the coagulation system [6].
The inductive method has some potential advantages over the commonly used numerical time-stepping methods (e.g. Runge-Kutta, Adam’s, Gear’s etc.). 1) The method provides a solution which depends continuously upon time, thus avoiding the need to interpolate the approximation which can in some circumstances result in large and unexpected inaccuracies in model predictions. 2) Since the inductive solution is based on an algebraic approximation to the nonlinear system over the whole time domain of interest (e.g. a dose interval) rather than a small fraction of the time domain that is considered by timestepping ODE solvers then it is expected that the method would work equivalently well for stiff or non-stiff systems. Although further work would be desirable to characterise this property. 3) The solutions to the derivatives of the model with respect to parameter values are available in analytical form. 4) Time-stepping methods that use adaptive step-size requires the parameters are fixed before solving, whereas the inductive method provides a closed form approximation that is valid for any arbitrary set of parameter values. This is of particular importance for subsequent inference based on evaluation of the likelihood, such as in parameter estimation or evaluation of the information matrix for design. 5) For the example considered here it was not a requirement to have informative starting conditions, i.e. parameter values, for the linearization.. The disadvantage of the inductive linearization is the need for the user to define the model to the level of a closed form integral of the linearized, time-varying, model. While this is an important initial limitation of the method automated methods to create this integral are available and can be applied to this setting.
We have provided code in Appendix A for the implementation of the inductive method in MATLAB for the example considered here, and this can be easily modified to apply to other nonlinear systems. Note that for any nonlinear system there will always be at most two integrals at each step in the inductive process (such as in (equation 9)), and that in some cases one or both of these integrals may be solved exactly. In this work we have made no attempt to optimize the speed or accuracy of the inductive method in order that the method can be shown in its simplest form. Here we have used Gauss-Legendre quadrature to give precise estimates to the integrals in the inductive approximations, but there are also other methods with similar accuracy that could be used, e.g. Gauss-Kronrod quadrature (which allows the error to be estimated) and Clenshaw-Curtis quadrature (see Trefethen[8]).
There are other methods of generating approximate solutions to nonlinear systems, including asymptotic approximations, methods can be found in Zwillinger [9]. In all of these cases however the behaviour of the system at local values of the parameters needs to be known in order for these approximations to work. The advantage of time-stepping ODE solvers and the inductive linearization method presented here is the limited dependence on the values of the parameters, with the caveat of the requirement for solvers of time stepping systems to be either stiff or non-stiff solvers.
In conclusion, we present a linearization method for converting a system of nonlinear ODEs into an iterative system of (usually timevarying) linear ODEs which can then be solved at each step using standard techniques.
Appendix A MATLAB code
function y = cn(t,n)
global d ka v km vmax N1 N2 x1 x2 w1 w2; % parameters
y = zeros(1,length(t));
if(n==1)
y = (ka*d/(v*(vmax/(km*v) - ka)))*(exp(-ka*t) ...- exp(-(vmax/(km*v))*t));
else
for j=1:N1
y1 = zeros(1,length(t)); for k=1:N2
y1 = y1 + (vmax/v)*(t*(1-x1(j))/4).*(w2(k)./(km + ...
cn(t*(x1(j)+3)/4 + t*(1-x1(j))*x2(k)/4,n-1)));
end
y = y + (ka*d/v)*(t/2).*w1(j).*exp(-ka*t*(x1(j)+1)/2 - y1);
end
end
Appendix B the integrating factor formula
Consider a system of first-order linear ODEs with time-varying coefficients, i.e. of the form:
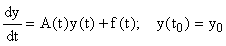 , (8)
, (8)
where  ,
,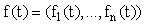 ,
,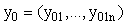 are (column) n-vectors, and A(t) is an n × n (non-singular) matrix. To solve the system we take the A(t)y(t) term to the left hand side (LHS) and multiply the whole equation by the integrating factor
are (column) n-vectors, and A(t) is an n × n (non-singular) matrix. To solve the system we take the A(t)y(t) term to the left hand side (LHS) and multiply the whole equation by the integrating factor 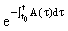 ,
,
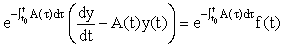
We then recognise that the LHS can be written as a derivative, i.e.
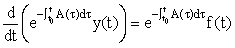
Integrating this equation from t0 to t, we derive the solution:
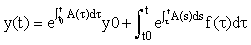
Even if they cannot be done exactly, the integrals in this formula can be transformed to integrals over the interval [−1,1] and hence estimated using Gauss-Legendre quadrature, i.e.
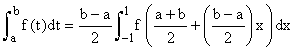
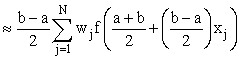
Where xj, wj are the abscissas and weights respectively for Gauss- Legendre quadrature.
Dr G Hegarty was supported by a School of Pharmacy postdoctoral fellowship.