Abdominal Aortic Aneurysm (AAA) is a localized dilatation of the abdominal aorta exceeding the normal diameter by more than 50 percent, and is the most common form of aortic aneurysm. The major complication of AAA is rupture, which is life-threatening and mortality of rupture repair in the hospital is 60% to 90% [1,2]. Nowadays Endovascular Aneurysm Repair (EVAR) is considered the treatment of choice for the majority of AAA since it demonstrates improved perioperative morbidity and aneurysm-related mortality, comparing to conventional open repair. However, despite the initial technical success and early discharge of the patient, this technique is associated with a unique set of complications, including endoleak, device migration and intraprosthetic thrombosis which mandate ongoing postoperative surveillance [3-11]. Currently the design of AAA endograft was a modular design with different lengths of graft main body and mating bilateral iliac limbs. The interior of the stent is a polyester fabric tube, while the exterior is covered by a metallic tube [4]. The hemodynamic changes that the endograft sustains during the follow-up period make it prone to positional changes with subsequent risk for endograft migration and the intraprosthetic thrombus formation, where the geometry of the endograft is one of the most important factors [9].

The size and the shape of the AAA vary among patients. The design and size of current devices are variable. Flow separation, flow recirculation and vortices inside these devices can cause platelet aggregation and endothelial hyperplasia leading to the formation of clots [12-15]. Furthermore, complications such as device migration may occur if the fixation force is inadequate to resist the drag force exerted on the endograft [16]. The purpose of this study is to analyze the analyzing the influence of endograft with different main body lengths on blood hemodynamics in AAA by computational fluid dynamics in finding the best geometry design to reduce intraprosthetic thrombosis and device migration with the intention to assess potential methods to reduce these endograft complications.

Model

The morphology of the patient’s AAA is obtained through Computed Tomography (CT) imaging, The TeraRecon Aquarius workstation (San Mateo, Calif) is used to trim the surface into a smooth curvature, and stent grafts with four different body lengths were drawn and placed in the AAA, as shown in Figure 1. The length, from short to long, are labeled as: No. 1=50 (mm), No. 2=70 (mm), No. 3=90 (mm) and No. 4=110 (mm). The stent model is divided into hexahedral element meshes before using the software Rhinoceros (Robert McNeel & Associates,Seattle, Wash)) to simulate the flow. The density for the blood characteristic in the simulation was 1050 (kg/m³) and viscosity coefficient: 3.5×10^-3 (Pa∙s) [17,18]. With this working assumption, the shear stress in the blood is proportional to the velocity gradient in the blood. A velocity waveform was inserted at the inlet border of the device and a pressure waveform was inserted at the outlet border (Figures 2A and 2B). Data for the velocity waveform and pressure waveforms had been described [19,20]. The cycle of the border condition was set at one second per heart cycle.

Figure 1: Stent grafts with four different body lengths (left column) in the abdomen aortic aneurysm.

Figure 2: (A) Inlet border of the device: velocity wave form, (B) outlet border of the device: pressure waveform.

Flow separation, flow recirculation and vortices

Computer-enhanced geometric modeling and Finite Volume Analysis have been used to study the biomechanical behavior of the aortic aneurysms before and after the insertion of the endograft device. Numerical modeling of endovascular-treated AAA is used to determine the stresses and forces developed on AAA sac and stent-graft materials in vivo, estimating hemodynamic parameters, such as the pressure and stress distribution over the main body, the bifurcation, the limbs of a stent-graft or the drag and displacement forces predisposing to graft migration. Finite Volume Analysis technique has a crucial role in the computational research of hemodynamic systems by solving Navier- Stokes equations for all finite volumes of the model, and it is the most applicable equations. The inertia of the fluids during the flow and the stress, viscosity exerted in the fluid field are balanced with other exterior forces through the equation. If exterior forces such as gravity are ignored, then the Navier-Stokes Equation along the flow line can be expressed as:

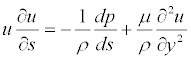
(s represents the coordinate along the flow line, while y represents the coordinate for the vertical flow line)

The presence of an adverse pressure gradient

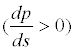
would decelerate (u) the velocity (s) of the flow field along the direction of the flow line. If the adverse pressure gradient is significant enough, the velocity may be reduced to 0, or even a negative value (reversed flow). When the velocity gradient in the border zone is reduced to 0

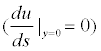
the flow is detached from the surface of the object to form a flow separation, this point is referred to as the separation point. In addition, flow recirculation is produced downstream, and is further developed into vortices. The researchers are able to analyze the separation, recirculation and vortices, of the blood in different lengths of the main body through computer simulation.

Drag force

The drag force generated by the blood fluid field against the stent graft can be categorized as the pressure drag force and the friction drag force. The pressure drag force is created by the impact of the blood pressure against the wall surface of the stent graft. The effect of its pressure is perpendicular to the wall of the stent graft, while the friction drag force is generated by viscous shearing stress. The effect of the shearing stress is parallel to the wall of the stent. The calculation of the drag force in the present study is to integrate the pressure of the stent wall and viscous shearing force against the affected area and the downward component is obtained from the sum. The relationship of the drag force with variations in the stent graft geometry was also related to different parameters of graft diameter, graft position, and graft curvature.

The results from the simulation showed that when the fluid field is decelerated to t/T=0.44, the flow field of the longest main body (stent no. 4), began to generate flow recirculation and vortices around the wall in the frontal plane (Figure 3). The area affected by the recirculation and vortices gradually increases in the frontal plane when the velocity of the fluid field of stent no. 4 is reduced to t/T=0.5, while the fluid field of stent no. 3 started to form recirculation and vortices in the frontal plane at this time (Figure 4A). The fluid field of stent no. 4 started to generate recirculation and vortices in the transverse plane when the velocity is reduced to t/T=0.5 (Figure 4B). The formation of the recirculation and vortices was not observed in stent nos. 1 and 2.

Figure 3: Frontal plane: recirculation and vortices around the wall in four different lengths of stent graft.

Figure 4: (A): At t/T=0.5, stent no. 3 started to form recirculation and vortices in the frontal plane. (B): At t/T=0.5, stent no. 4 started to generate recirculation and vortices in the transverse plane.

The drag force that caused device migration is the sum of the pressure drag force and the friction drag force being applied on the stent wall. The results from the simulation indicated that the pressure drag force was the major force causing device migration when the friction drag force caused by viscous shearing force was 1~3% of the total drag force. The amount of drag force received by stent no. 1 to 4 in one heart cycle (Figure 5).

Figure 5: The amount of drag force from stent no. 1 to 4 in one heart cycle.

The recirculation and vortices formed in the main body may damage the neo-endothelium and cause the blood inside the stent to form clots and obstruction after the endograft implantation in AAA. The incidence of the clot formation increases as the length of the stent main body becomes longer [9]. Our model is based on approved devices. We have not modelled it on the above, which may be an area of further research [22]. The results of the simulation in the present study showed the formation of vortices in stents with a longer main body increased when the velocity of the fluid field was reduced. Due to the effects of the reverse pressure gradient on the fluid field, the velocity of the fluid field was reduced as well as gradual reduction in the velocity of the border zone in the fluid field. A separation was formed in the fluid field when the border zone velocity gradient reaches 0 and recirculation was generated downstream to the stent main body, which further developed into vortices. Pressure simulation of stent no. 4 showed the formation of recirculation and vortices when the fluid field decelerated in the stent and when the heart cycle is t/T＝0.44 and 0.5. A reverse pressure gradient was present in the fluid field (Figure 6). With the blood density maintained at a constant, the velocity was further reduced as the cross-sectional area of the channel increased. When the fluid field was affected by the reverse pressure gradient, recirculation was formed at the downstream to the fluid field in the stent main body which was further developed into vortices. The occurrence of separation in the main body could be avoided with shorter length. This would avoid the formation of recirculation and vortices of the fluid field in stent grafts, thus reducing the incidence of recirculation and vortices. Furthermore, other than the loss of fluid energy caused by the friction between fluid viscosity and the wall when the fluid was flowing through the channel, the curvature, and the changes in cross-section of the channel might cause the loss of fluid energy leading to a reduced inertia of the border zone. Separation was generated when its velocity gradient reached 0 and recirculation and vortices were formed. The formula for the energy in the channel was shown below:

Figure 6: Pressure simulation showed the formation of recirculation and vortices when the fluid field decelerated in the stent. A reverse pressure gradient was present in the fluid field.

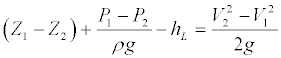
(V: mean velocity of the flow in the channel; Z: the height from the base level; P: channel flow static pressure;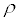 : fluid density in the channel; g : acceleration of gravity; L _h : loss of energy; subscripts 1 and 2 indicate upstream and downstream of the channel)

When the effect of gravity was ignored, the inertia of the fluid applied on the fluid field became negative when the fluid field was under a reverse pressure gradient 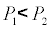), and the inertia of the fluid was reduced. When there was an increase in viscosity and the curvature of the channel, and the changes in the cross-sectional area increased the energy loss (h_L), which also increased the inertia loss. As the degree of curvature of the abdominal aorta neck changed the blood flow model, the incidence of thrombus formation increased as the cross-sectional area of the stent in/outlet increases [9,21]. The reduction of fluid energy loss should be minimized, to avoid stagnation of the blood in parts of the stent where blood clots can form, and should be considered when designing stents.

In terms of the drag force on the stent, the results of the simulation showed that as the pressure increases, the drag force increases as well. However, the amount of drag force received by the four main body lengths is almost similar as the drag force varies with the changes in pressure wave form that ranges between 2.8 to 4.8 (N). Results from the simulation by Zhonghua Li et al. and the present study showed that the drag force in the stent is mostly caused by the impact of blood pressure against the stent wall; the drag force increases as the blood pressure increases [16].

Blood clots formed inside the stent that travel with the blood flow is referred to as an embolus. Embolus may obstruct peripheral arteries such as the renal artery, internal and external iliac artery, and femoral artery. A thrombosis causes the disruption of blood flow and may induce further complications, such as: lower body paralysis caused by the obstruction of important blood vessels that supply blood to the spine. Ischemia of the intestine can lead to necrosis if the blood supply to the colon is affected. Device migration may cause a type I endoleak, which may lead to the further expansion of AAA, or even a rupture. Through computerized simulation and fluid dynamic analysis prior to the manufacturing of artificial stents, we may obtain an initial understanding of the fluid field in the stent after the endograft is implanted; in addition, design and research and development of the stent to address post-surgery complications of the endovascular aneurysm repair can be addressed. The results from the simulation in the present study showed that recirculation and vortices in the stent may be avoided in stents with a shorter main body, which can reduce the incidence of clot formation. Furthermore, the drag force that causes device migration is not associated with the length of the stent main body. A recommendation is made to implement stents with a shorter main body when performing endovascular aneurysm repair based on the findings above.