Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
+44-77-2385-9429
ISSN: 2168-9792
+44-77-2385-9429
Research Article - (2016) Volume 5, Issue 1
Surface roughness is a principal measure of product quality of the materials used for sophisticated applications. The present paper reports an experimental investigation of various parameters related to the surface roughness of the materials used for the aerospace applications by an inexpensive non-invasive technique known as speckle photography. Conventional non-destructive testing techniques such as X-Ray imaging, ultrasound scanning, microwave testing etc, have certain limitations on testing the surface characteristics of low modulus aerospace vehicle components. This paper explains characterization of surface roughness by analyzing certain roughness parameters such as intensity distribution, size distribution and contrast ratio of different low modulus materials used in aerospace applications. The optical setup employed for the work is simple and uses an inexpensive digital camera for grabbing the specimens under different static conditions
<Keywords: Laser speckle photography; Surface roughness; Aerospace applications; Non-destructive testing
Measurement methods based on the speckle phenomenon have become increasingly important in recent years [1]. Speckle metrology encompasses a range of techniques that are utilized for non-contact, fullfield inspection of diffusely reflecting surfaces [2]. Speckle techniques rely on the illumination of region of interest on a diffuse surface with an expanded laser beam to produce a speckle pattern. The principal speckle techniques such as speckle photography, speckle interferometry and speckle shearography have already been established to be emerging optical NDT techniques for structural inspection [3]. Out of the three techniques, speckle photography is the simplest scheme to set up and operate in speckle metrology [4]. In this technique, the speckle patterns of the specimens are recorded by use of a CCD camera and are then analyzed by digital image processing algorithms to obtain parameters that describe the surface roughness [5]. The surface roughness can be regarded as a variation of the surface height and there exists a copious number of parameters to characterize the surface roughness that must be considered [6]. This paper illustrates the utilization speckle photography for surface roughness assessment of certain low modulus rubberized constituents used for aerospace applications. Since aerospace technology demands stringent quality requirement, the constituents utilized are to be accessed by different means. The conventional methods like x-ray imaging, ultrasound scanning, acoustic and microwave analysis have certain restraints in giving the surface roughness properties of low modulus materials. Generally, x-ray does not give good surface images of rubberized compounds. The low modulus materials completely absorb acoustic waves, making ultrasound imaging not feasible. The microwave is not suitable for these specimens due to its high wavelength compared to laser sources used in optics experiments [7]. The proposed speckle photography experimental setup can be easily configured with computer system and further analysis can be performed using image processing software. The specklegrams of the specimen are grabbed under different static conditions. Since the specklegrams and its characteristics are different for each surface, one or more of the attributes of specklegrams such as contrast ratio, size distribution, intensity distribution and correlation between the different areas may change. In the present experiment, the properties such as contrast ratio, intensity distribution and size distribution have been studied for three different low modulus materials and are compared to a glass surface.
The basic characteristic of the speckle pattern is its randomness. This randomness is caused by the surface roughness because the phase of the light scattered will vary from point to point in proportion to the local surface height [8]. Since speckle patterns are produced by the roughness of a surface, it is reasonable to assume that the statistics of the speckle patterns produced might be used to provide a measure of this roughness [9]. At this juncture, the statistical properties of image speckle patterns in relation to the surface roughness of objects have been studied in depth with the condition that the surface, comprising of several independent scatterers, constructs a complex Gaussian random amplitude distribution at the image surface [10]. Goodman communicates a comprehensive treatment of the statistical distribution of speckle patterns originating from various rough surfaces [11]. The amplitude of the intensity field at a given observation point (x,y) consists of a multitude of de-phased contributions from different elementary scattering areas on the rough surface. Consequently, at a specific distance from a source, a group of plane wave fronts propagating in space is denoted by a random phasor sum. A Random phasor sum is statistically represented as [12].
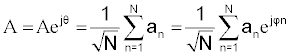 (1)
(1)
This phasor sum can be considered as a random walk in the complex plane where ‘N’ represents the number of phasor components in the random walk, ‘A’ is the resultant phasor, ‘A’ is the length and ‘θ’ is the phase of the resultant phasor. Further, an is the nth component phasor in the sum. The scaling factor 1/√N is introduced to preserve the finite second moment of the sum even when an approaches infinity. Finally, an represents the length and represents the phase of an.
The joint probability density function P for the real and imaginary parts of the resultant phasor is given by
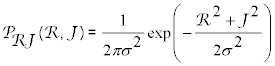 (2)
(2)
Where σ2 = σR2 = σJ2 denotes variance of real (R) and imaginary (J) parts of the resultant phasor. Hence, the marginal statistics of the length A turn out to be
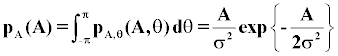 (3)
(3)
This is known as the Rayleigh density function and its typical plot for A ≥ 0, is shown in Figure 1 The marginal statistics of the phase θ is found by
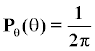 (4)
(4)
for − π ≤ θ ≤ π. Here it is used that the integral of the Rayleigh density function must be unity.
For a speckle pattern, there are a large number of contributing amplitudes. So, the result obtained for random walks with large number of independent steps is used for plotting the Rayleigh probability function.
Applying the transformation laws, for a sum of complex field amplitudes with uniformly distributed phases, Goodman and others have shown that the intensity I, displays a negative exponential probability density function.
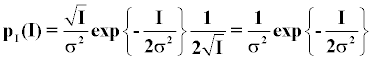 (5)
(5)
for I ≥ 0, equation (5) can be modified to obtain a fully developed speckle
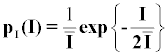 (6)
(6)
Thus the magnitude of the resultant speckle field follows a Rayleigh probability distribution, the phases are uniformly distributed between [−π, π] and the speckle intensities distribution can be described by a negative exponential distribution as shown in Figure 2.
The experimental arrangement is shown schematically in the Figure 3. The specimens under investigation are coherently illuminated by means of a 10 mw He-Ne laser operating at 632.8 nm.
To begin with, the laser beam is expanded by a beam expander optics to illuminate the mirror M1. The beam thus deflects off from the mirror M1 passes through a spatial filter arrangement. Another mirror M2 guides the spatially filtered beam towards the test specimen. The object beam from the each sample is steered on a 9.1 megapixel digital camera (Sony DSC-H50) where resultant speckle patterns are captured. These patterns are then transferred to a computer for further processing of the images. The specimens (1-3) used for this current experiment are rubberized diffusing materials used for aerospace applications whilst the specimen (4) is a well scratched glass plate. The entire experimental setup has been arranged on a vibration isolation table. Trial experiments are conducted before recording the specklegrams for achieving better stability of the table within the vibration isolation environment and for achieving the steady state focusing. A program has been scripted using MATLAB and C for processing the specklegrams and to analyze the surface roughness properties such as intensity distribution, contrast ratio and size distribution. Several trial exposures are taken for grabbing specklegrams of the specimens with different aperture sizes such as f/2, f/4, f/5, f/8 at a shutter speed of 1/20 Sec. It has been spotted that the images obtained with an aperture size f/4 has given high contrast specklegrams for further analysis and are shown in Figure 4.
An experiment has been performed in order to investigate the effect of intensity distribution, contrast ratio and size distribution of the speckle on surface roughness assessment.
Intensity distribution
The intensity distribution of the specklegram will be random, with a normal distribution [13]. The scattered intensity distribution produced by the four specimens is curve fitted with a matlab Gaussian peak model. The Gaussian model is provided by the equation (6) where a corresponds to amplitude, b is the centroid location, c is related to peak width and n is the number of peaks to fit the random independent variable x.
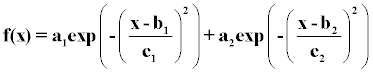 (7)
(7)
The intensity distribution of the speckle pattern generated by the specimens is fitted to the Gaussian model as shown in Figures 5-9. A comparison of fitting curves for all the specimens is presented in Figure 9.
Thus, the intensity distribution of the specklegram is normally distributed at random. The fitting shows that it is almost the same as Rayleigh distribution and in agreement with the theoretical results. The analysis of the specimens used leads to a fact that though the distribution remains Gaussian, the distribution parameters change for all the four specimens and that can be exploited to contribute more information about the type of material.
Contrast ratio
The intensity statistics of the speckle pattern can be well explained by the contrast ratio measurements [14]. The speckle contrast ratio, the ratio of maximum to minimum intensities, is a scale of the speckle intensity variation [15-19]. Since maximum intensity possible for a monochrome pattern is 256, contrast ratio will be between 0 and 256. The noise resulting from the recording instruments is eliminated by trial experiments as they may cause a difference in the actual minimum and maximum point.
The contrast ratio analysis has been performed on all the specimens and is shown in Table 1. The contrast ratio of the specklegram depends on the roughness of the surface on which specular reflection is happening. When roughness of the surfaces increases, the contrast ratio will also be increased.
| Specimen | Contrast Ratio |
|---|---|
| Specimen 1 (Roughest Surface) | 79 |
| Specimen 2 (Medium roughness) | 14. 14 |
| Specimen 3 (Least roughness) | 7. 54 |
| Specimen 4 (Scratched Mirror) | 58 |
Table 1: Contrast ratio for different specimen.
Size distribution
The size of the speckle has also been considered for the present study. The size of the individual speckle depends on the illumination area, the wavelength of illuminating light, etc. In order to calculate the size distribution, the obtained grayscale specklegram is converted to black and white image using a mean threshold value and then the size of the white spots is measured. The equation used for the best fit for the present size distribution has been selected as
f(x) = a exp (bx)
The fitting obtained for the size distribution of the specklegrams (Figures 10-14) is exponential and in agreement with Figure 2.
Even though the size distribution remains exponentially decreasing for all the surfaces, it can be seen that there are slight changes in the fitting parameters. It should be pointed out that for the low modulus materials, the peak size can be seen as 350 units whereas for the Glass the peak size is around 600 units. Thus, the change in material is observed to be producing the change in the size of the speckle. Thus, materials can also be characterized using the maximum speckle size that is obtained using a particular wavelength.
The present work exploited speckle photography as a method to characterize different surface roughness properties of materials using an indigenous low cost method. The intensity distribution of the specklegram is normally distributed at random. The fitting shows that it is identical with Rayleigh distribution and is in agreement with the theoretical results. The contrast ratio of the specklegram depends on the roughness of the surface from which specular reflection occurs. The materials can also be characterized using the maximum speckle size that is obtained using the required wavelength.
All authors acknowledge the Department of Science and Technology (DST) and University Grant Commission (UGC) for the financial support. V P N is thankful to Kerala University and International School of Photonics.