Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2018) Volume 7, Issue 2
The Lambert guidance method has been widely used to steer the ballistic missile in the boost phase. However, only the two-body dynamics-based Lambert algorithm is valid in most practical applications due to the high requirement for computing efficiency. To deal with this problem, an analytical state deviation prediction model of missile subject to J2 perturbation term is proposed in this paper. The differential equation with respect to state deviation vector of missile is built in the Local-Vertical-Local- Horizontal (LVLH) frame, and the state transition matrix of this differential equation obtained in previous work is used to derive the analytical state deviation prediction model based on the linear system theory. The J2 term gravitational acceleration is regarded as perturbing term in this differential equation and is also expressed in the LVLH frame by using the knowledge of spherical trigonometry to satisfy the conditions of analytical solution derivation. By using this analytical model, the impact deviation of missile caused by the J2 term can be calculated in each guidance cycle. Then the velocity required to hit the target is modified by a feedback algorithm. Simulations conducted in this paper have verified the accuracy of this analytical model and its effectiveness in the missile guidance applications
Keywords: Analytical solution; Ballistic missile; Lambert guidance algorithm; State space perturbation method; J2 perturbation
Since proposed, the Lambert guidance method has been serving as the fundamental guidance algorithm for ballistic missile or another booster spacecraft [1]. By solving the Lambert problem, this method can be used to calculate the required velocity vector to travel ballistically from position 1 to position 2 in a predetermined time of flight [2]. Due to the limitation of the guidance cycle, the two-body assumption is considered in most practical applications. However, the J2 term gravitational perturbation of the earth has a significant effect on suborbital vehicles, such as ballistic missiles. For the intercontinental ballistic missile (ICBM) with a range of 10000 km, the impact error caused by the J2 term would exceed 10 km in most cases. To eliminate the influence of J2 term gravitational perturbation in the Lambert guidance routine, the impact state deviation should be predicted in a very short time and then correct the required velocity by the feedback algorithm.
In order to deal with this problem, several technologies had been used to build the fast state deviation prediction model in the past. Chen [3] and Ma [4] obtained such a model based on the neural network technique and a mapping relationship between the current state vector (contains the position and velocity vector) of missile and the corresponding impact state deviation as well as the flight time deviation is trained in their models. These methods have relatively high accuracy and no restriction on the form of perturbing force. However, it would take a lot of time to generate samples and train the neural network model for each trajectory, which weakens the fast launching capability of the missile.
Deducing the analytical solution of a body’s motion perturbed by the J2 term gravitational acceleration is another effective way to the deal with the aforementioned problem. In fact, this method belongs to the domain of orbital perturbation theory and is well known as the general perturbation method in such theory [5]. The general perturbation method mainly consists of the average method and linearization method, and the former initially proposed by Brouwer [6] and Kozai [7] has been widely used for long-term orbit propagation in the field of artificial satellites. Many improvements have also been done in recent decades to obtain higher precision and eliminate the singularities [8-16]. By using the mean orbit elements, the average method can predict the satellite’s state accurately, even if the prediction time interval is longer. However, the average method, in the context of computing mean elements by iterative algorithm, is very difficult to implement onboard real-time state deviation vector computation due to its complexity [17].
Compared with the average method, the linearization method does not provide an exact description of the motion, but it is an enormously valuable tool when used to short-term orbit prediction. Basically, the approach is to linearize the equations of motion by a series expansion about a nominal or reference orbit in which only first-order terms are retained. For the results to remain valid it is necessary to restrict the magnitude of the deviations from the nominal orbit [5]. Ren [18] initially derived the explicit expression of the state transition matrix for the perturbed Keplerian motion with respect to true anomaly. Zheng [19] improved this method in his PhD’s thesis and named it State Space Perturbation Method (SSPM). Simulations in Ref. [19] have shown that the SSPM have many advantages when used to analyse the state error propagation of missile in gravity anomaly field.
In this context, the expression of J2 term’s gravitational potential is transformed from the earth-centred inertial reference frame (ECI) to the Local-Vertical-Local-Horizontal (LVLH) frame according to the knowledge of spherical trigonometry. Then the analytical solution for state deviation of missile is derived based on the SSPM. By using this analytical model, the impact deviation of missile caused by the J2 term can be calculated in each guidance cycle, and the velocity required to hit the target is modified by a feedback algorithm. Simulations conducted in this paper have verified the accuracy of this analytical model and its effectiveness in the ballistic guidance applications.
The following sections are organized as follows. Section 2 briefly introduces the SSPM and Lambert guidance algorithm. Section 3 studies the coordinates transformation method of J2 term and derives the analytical solution for missile state deviation prediction. Section 4 gives the feedback correction algorithm for the Lambert guidance routine based on the proposed analytical state deviation prediction model. Section 5 analyses the accuracy of this analytical model and its effectiveness in the ballistic guidance applications, and Section 6 concludes it.
The basic knowledge used in this paper is introduced in this section, mainly the SSPM and the Lambert guidance routine for ballistic missile.
State space perturbation method
The perturbed differential equation of missile’s motion in the LVLH frame, as shown in Figure 1, can be expressed as
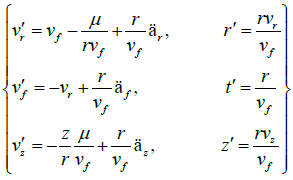
The superscript of ' in Equation 1 denotes the differential operator with respect to the true anomaly. vr, vf and vz are the components of velocity vector in the LVLH frame rand z are the components of position vector. t denotes the flight time of missile from the initial point. dr, df and dz are the components of the perturbing force vector, and µ is the gravitational constant of the earth.
Let Xref and X respectively represent the nominal state vector and true state vector of missile, or
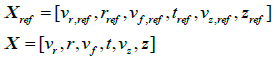 (2)
(2)
Then the differential equation of nominal motion and true motion can be rewritten in vector form as
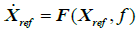 (3)
(3)
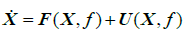 (4)
(4)
It is noticed that the perturbation term U(X,f) is small. Let expands Equation 4 at Equation 3 by Taylor series and retains the first-order terms, then one gets
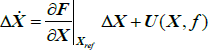 (5)
(5)
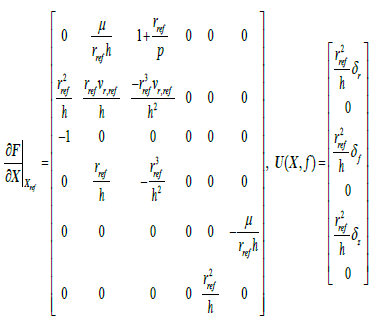 (6)
(6)
where ΔX is called the state deviation vector, i.e. ref ΔX = X - Xref . h is the magnitude of angular momentum vector and p is the semi-latus rectum of the nominal orbit?
Ren [18] has derived the six-dimensional state transition matrix Ф( f1 , f0 ) of Equation 5 by using variable substitution, and expressions for every element of Ф( f1 , f0 ) are listed in Appendix A. According to the linear system theory, for systems subjected to continuous disturbance, the state vector at f1 can be calculated by
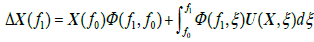 (7)
(7)
Lambert guidance
Generally, the state equation of the missile system in boost phase can be expressed as
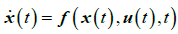 (8)
(8)
And, the purpose of guidance system for ballistic missile is to generate a set of steering commands to transfer the controlled system from t0 at the time of t0 to the required terminal state x(tf) at the time of vR . The Lambert guidance has been used to control a missile during the third stage of the boost phase to hit a target point on the ground downrange in a desired time [20,21]. In this guidance routine, the Lambert problem is solved at each integration time step to calculate the required velocity vR . The current missile velocity v0 is subtracted from the required velocity Δv to compute the velocity to be gained, i.e. Δv as shown in Figure 2. The missile is commanded to accelerate in the direction of Δv . Missile thrusting is terminated when r0 reaches a threshold tolerance level, and then the missile flies ballistically to the intended target.
In Lambert’s problem we are given r0, rF and tF as shown in Figure 2, then seek to find the velocity v and flight-path angle γ. So we must use the iterative method to solve the Lambert problem. In order to speed up the iteration efficiency, Paul Zarchan [22] has found that the valid flight-path angle for ballistic missile have upper and lower bounds, and they yield
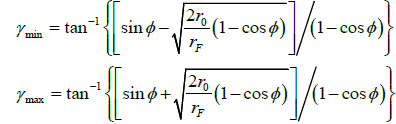 (9)
(9)
The initial guess of the flight-path angle is generally set as the average of the minimum and maximum flight-path angle
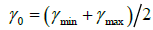 (10)
(10)
Then the velocity v and the corresponding flight time tF0 can be obtained by,
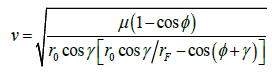 (11)
(11)
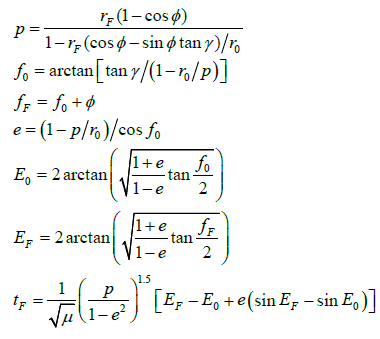 (12)
(12)
where the central angle f yields
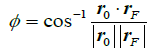 (13)
(13)
In the iteration process, the flight-path angle updates as the following formula
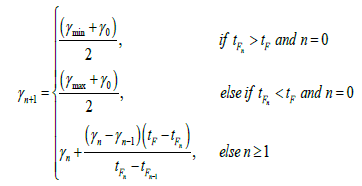 (14)
(14)
The iteration is terminated when the computed flight time tFn is sufficiently close to the desired flight time tF.
Analytical State Deviation Prediction Model Derivation
In order to obtain the analytical solution of state deviation vector according to Equation 7, the gravitational potential of J2 should be expressed in the LVLH frame. In the earth-centered inertial reference frame (ECI), the gravitational potential of J2 denoted by U2 can be shown as
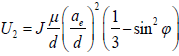 (15)
(15)
where J = 3J2/2 and ae is the equatorial mean radius of the earth. Equation 15 illustrates that the gravitational potential of J2 for arbitrary point in space only has relationship with the geocentric latitude f and geocentric distance d.
Figure 3 shows the transformation schematic diagram of U2 from the ECI frame to the LVLH frame. N is the north celestial pole. M is called the “new” north celestial pole, and OM is perpendicular to the nominal orbital plane OLE. L, E and R are the projection points of initial position, current nominal position and true position on the surface of this celestial sphere, respectively.
Let ( γM,ϕM ) and (γL,ϕL ) denote the coordinates of M and L , respectively. And let γ denote the spherical azimuth at point L . In the spherical triangle of LMN , one can obtain the following equations according to spherical trigonometry
 (16)
(16)
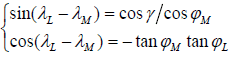 (17)
(17)
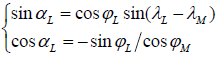 (18)
(18)
Since φL, λL and γ can be calculated directly when the state parameters of point L are given, one can obtain the value of φM, λM and αL by Eq.(16)-(18). In spherical triangle of RNM, the cosine of angle ΔNOR can be calculated by
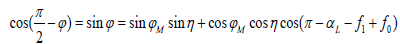 (19)
(19)
where f0 and f1 are the true anomalies at the initial and terminal position, respectively. Considering that the lateral angle n has a very small value, let substitute Equation 19 in Equation 15 and ignore the second-order small quantities with respect to η , then we obtain
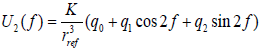 (20)
(20)
where K=Jµa2e/2 and the coefficients of pi, i=0,1,2 yield
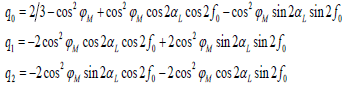
The gravity vector of J2 term in the LVLH frame can be derived by
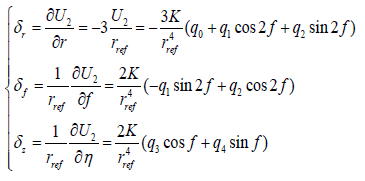 (22)
(22)
with
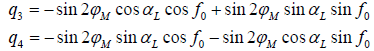 (23)
(23)
To make the expression simpler, let rewrite Equation 22 by
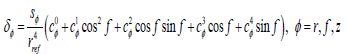 (24)
(24)
with
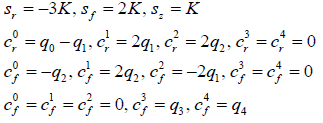 (25)
(25)
Substituting Equation 22 in Equation 7 and then one would obtain the analytical solution for every variable of ΔX
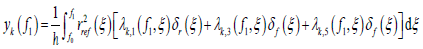 (26)
(26)
where ykf1,K= 1, 2, , 6 refer the component of ΔX, and λi j i j = 1, 2, , 6 represent the elements of the six-dimensional state transition matrix Φ( f1, f0 ) .
To make the derivation process clear, the complete details of derivation for the first component of ΔX is listed below.
Substituting the expressions of λ1,s(f1,ξ) s =( 1,3,5) into y1(f1), and we have
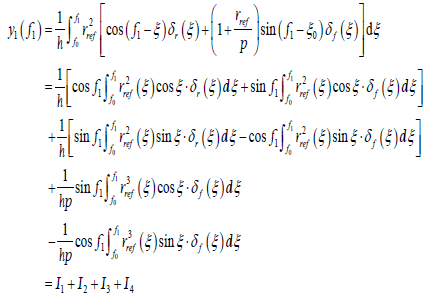 (27)
(27)
From Equation 27 we know that this expression contains a set of integral functions, and the integrand can be expressed as the form of g(ξ)•δφ(ξ). According to the form of g((ξ) these integral functions are divided into four groups. Substituting Equation 24 into Equation 27, then we obtain
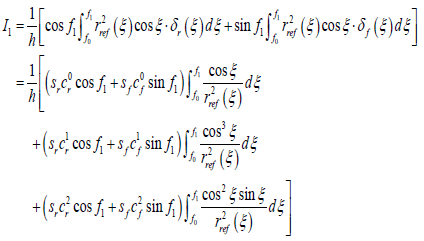 (28)
(28)
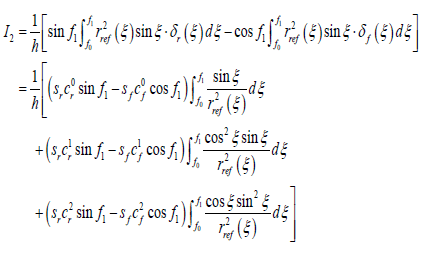 (29)
(29)
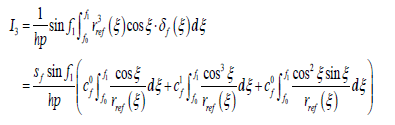 (30)
(30)
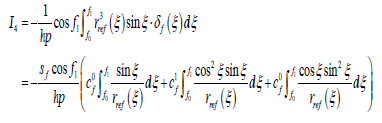 (31)
(31)
The integral terms in these expressions are all integrable. Let llm(f) denote a kind of integral function, and its definition is
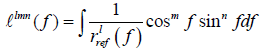
For different nonnegative integer of n, m and n , this integral function has the closed-form solution about f, e and p, and the expressions of llm(f) involved in the derivation of yk(f1) have been listed in Appendix B.
To simplify the expressions of Equation 28 to Equation 31, let re-express the definite integral functions in these equations by a set of ordered symbols, i.e. Δm,j m = 1,2,.., j = 0,1,.., 4 , where m represents the category of the integrand. For instance, four kinds of integrand exist in y1(f1), i.e. Ii, i=1,2,3,4. The expressions of Δm,j involved in yk(f1) as well as other components of yk(f1) are all listed in Table 1.
| m | j=0 | j=1 | j=2 | j=3 | j=4 |
|---|---|---|---|---|---|
| 1 | l210(f1)-l210(f0) | l230(f1)-l230(f0) | l221(f1)-l221(f0) | 0 | 0 |
| 2 | l201(f1)-l201(f0) | l221(f1)-l221(f0) | l212(f1)-l212(f0) | 0 | 0 |
| 3 | l110(f1)-l110(f0) | l130(f1)-l130(f0) | l121(f1)-l121(f0) | 0 | 0 |
| 4 | l101(f1)-l101(f0) | l121(f1)-l121(f0) | l112(f1)-l112(f0) | 0 | 0 |
| 5 | l100(f1)-l100(f0) | l120(f1)-l120(f0) | l111(f1)-l111(f0) | 0 | 0 |
| 6 | l001(f1)-l001(f0) | l021(f1)-l021(f0) | l012(f1)-l012(f0) | 0 | 0 |
| 7 | l010(f1)-l010(f0) | l030(f1)-l030(f0) | l021(f1)-l021(f0) | 0 | 0 |
| 8 | l002(f1)- l002(f0) | l022(f1)-l022(f0) | l013(f1)-l013(f0) | 0 | 0 |
| 9 | 0 | 0 | 0 | l112(f1)-l112(f0) | l103(f1)-l103(f0) |
| 10 | 0 | 0 | 0 | l210(f1)-l210(f0) | l201(f1)-l201(f0) |
| 11 | 0 | 0 | 0 | l120(f1)-l120(f0) | l111(f1)-l111(f0) |
| 12 | 0 | 0 | 0 | l111(f1)-l111(f0) | l102(f1)-l102(f0) |
Table 1: Expressions of Δm,j .
With Δm,j , the expressions of Equation 27 can be rewritten as
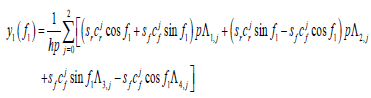 (33)
(33)
The analytical solutions for other elements of ΔX can also be derived by the same process, and the ultimate results are listed below.
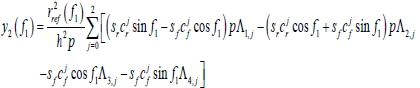 (34)
(34)
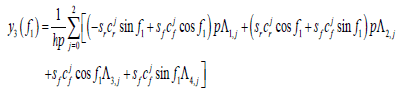 (35)
(35)
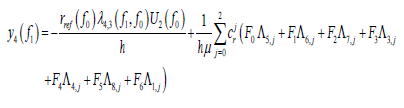 (36)
(36)
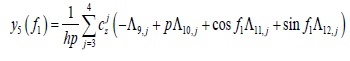 (37)
(37)
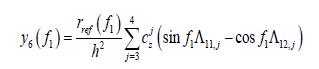 (38)
(38)
where
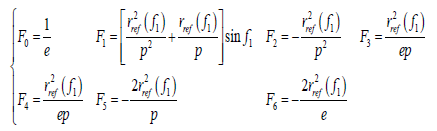 (39)
(39)
Feedback Correction Algorithm for the Lambert Guidance Routine
An effective strategy, which is known as the virtual target method, is used in this paper to offset the impact deviation caused by the J2 term gravitational acceleration in the Lambert guidance routine. Let first introduce the concept of Virtual Target (VT). As shown in Figure 4, T denotes the target point, and the reference trajectory is designed based on the two-body dynamics. H denotes the actual impact point under the influence of perturbing force. The VT denoted by is defined as the symmetry point of H in the local inertial frame of T-xyz.
From the definition of VT, it is easy to know that the actual impact point would be very close to the target point when the required velocity vector was calculated based on the VT in the Lambert guidance routine.
It is noticed that the impact deviations in the down range and cross range direction, respectively denoted by Δx and Δz, are required to calculate the coordinates of VT. Therefore, we need transform the state deviation ?X obtained by Equation 33 to Equation 38 to ?x and?z. In fact, the relationship between these two kinds of impact deviations yields
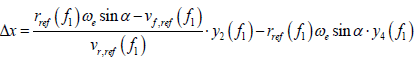 (40)
(40)
where ωe refers to the earth’s rotation angular velocity and α is the angle between the motion direction of missile and the north at the target point.
Numerical simulations are conducted here to verify the accuracy of the presented analytical state deviation prediction model and its effectiveness in the ballistic guidance applications.
Numerical simulation
This analytical model is used to predict the impact state deviation of missile with a range of about 10000 kilometres, and the numerical integration method is also used to calculate the exact solution of the state deviation to reveal the accuracy of the former. The exact impact state X of missile in the LVLH frame is calculated by numerically solving the differential Equation 1, and the impact reference state Xref is obtained based on the two-body orbit theory, and each component of Xref has closed-form expression, or,
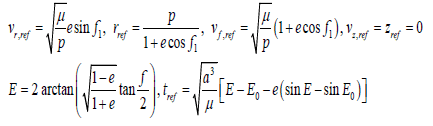
then the exact impact state deviation denoted by ΔXnumerical yields ΔXnumerical=X-Xref.
The initial parameters given in the form of orbit elements are listed in Table 2.
| Parameters | unit | Symbol | values |
|---|---|---|---|
| Semi-major axis | (km) | a | 6178 |
| Eccentricity | -- | e | 0.43 |
| Inclination | deg | i | 0-180 |
| RAAN | deg | W | 0 |
| Argument of perigee | deg | w | 270 |
| Initial true anomaly | deg | f0 | 120 |
| Terminal true anomaly | deg | f1 | 233 |
Table 2: Initial Conditions.
The numerical integration is carried out using fixed-step fourthorder Runge-Kutta method. The analytical solutions are obtained by Equation 33 to Equation 38. Since the impact position deviations in the down range direction and cross range direction are focused in the application of ballistic missile, the state deviations calculated by the analytical model and numerical integration are both transformed to Δx and Δz based on equation 40.
Table 3 illustrate the comparison results between the numerical solution and analytical solution. From these results, we can know that the impact deviations caused by the J2 term gravitational acceleration can reach the magnitude of 10 kilometers, and should not be ignored in the missile guidance routine. Moreover, both the down range deviations and the cross range deviations calculated by these two methods are very close for different initial inclinations, and the residuals of the presented analytical model relative to the numerical method are plotted in Figure 5. It is clear that the residuals are all less than 20 meters under each initial conditions.
| Inclination (deg) |
Numerical solution | Analytical solution | ||||
|---|---|---|---|---|---|---|
| (km) | (km) | Time consumption (s) | (km) | (km) | Time consumption (ms) | |
| 0 | -24.8767 | -0.0297 | 0.4250 | -24.8948 | -0.0297 | 0.8770 |
| 18 | -23.5423 | -8.7066 | 0.4400 | -23.5545 | -8.7184 | 0.8820 |
| 36 | -19.9820 | -13.8612 | 0.4350 | -19.9809 | -13.8663 | 0.8730 |
| 54 | -15.3328 | -13.4424 | 0.4480 | -15.3204 | -13.4308 | 0.8730 |
| 72 | -11.1655 | -7.8292 | 0.4360 | -11.1484 | -7.8138 | 0.8680 |
| 90 | -9.3060 | 0.2654 | 0.4280 | -9.2883 | 0.2664 | 0.8680 |
| 108 | -11.3994 | 7.3769 | 0.4430 | -11.3811 | 7.3643 | 0.8740 |
| 126 | -17.5699 | 11.1407 | 0.4370 | -17.5551 | 11.1317 | 0.8740 |
| 144 | -25.6775 | 10.6965 | 0.4470 | -25.6773 | 10.7014 | 0.8640 |
| 162 | -32.4193 | 6.4611 | 0.4310 | -32.4395 | 6.4708 | 0.8700 |
Table 3: Comparison between the numerical solution and analytical solution.
Besides, the simulation computations in this paper are performed with a 2.1 GHz Intel Core i5 Processor and 2 GB of RAM. The algorithm is coded in VC6.0 and compiled in 32-bit windows system. Under these conditions, the analytical solution with respect to the J2 term takes an average of 0.8723 ms, and the numerical integration method takes an average of 0.437 s. The onboard guidance cycle of missile is usually set as 0.02 seconds, which means the presented analytical model has enough efficiency when used for real-time state deviation prediction in the Lambert guidance routine.
The effectiveness of the proposed analytical state deviation prediction model in the missile guidance applications is tested under three cases with the range of 7912.3km, 9796.6km and 12273.9km, respectively. In this simulation, we assume that the missile is boosted by three stage engines. The tracking guidance algorithm is used in the first two stage flight segments to make the missile approximately approach the pre-designed state, and the Lambert guidance algorithm is implemented in the third-stage flight segment to ensure the burnout precision.
The initial weight of missile at the beginning of the Lambert guidance process is all 4000 kg. The specific impulse is 250 seconds. The initial positon components of missile in the earth centered inertial frame (ECI) are -2610.351 km, 3735.302 km and 4630.187 km, and the initial velocity components are -3623.1 m/s, -119.0 m/s and 1420.4 m/s. The thrust of engine for these three cases are 162 kN, 171 kN and 180 kN. The nominal burn time for these three cases are 44.2 s, 46.9 s and 49.5 s. The trajectory profiles for these three cases are shown in Figure 6.
Table 4 shows the comparison results between the Lambert guidance routine without correction and the one with correction. The simulation results imply that the Lambert guidance algorithm has high precision if we neglect the perturbing factors, and both Δx and Δz are all less than 1 m in each case. However, the impact deviation exceeds 10km when the J2 term gravitational accelerations are involved, which coincides with the conclusion from Table 3. When the influence of the J2 term gravitational accelerators are corrected by using the concept of virtual target point, the impact deviations of Δx and Δz reduce to less than 21 meters.
| Range | Perturbation terms considered | Lambert guidance without correction | Lambert guidance with correction | ||
|---|---|---|---|---|---|
| (m) | (m) | (m) | (m) | ||
| Case 1 | None | -0.1051 | -0.9572 | -0.1051 | -0.9572 |
| 11130.8283 | 8953.5293 | -20.1121 | -8.4114 | ||
| Case 2 | None | 0.4747 | 0.3540 | 0.4747 | 0.3540 |
| 12632.3007 | 9935.9203 | -11.4212 | -2.1956 | ||
| Case 3 | None | 0.4791 | 0.1218 | 0.4791 | 0.1218 |
| 13010.7619 | 9245.0010 | 0.7966 | 0.8427 | ||
Table 4: Comparison between these two Lambert guidance routines.
In order to verify the adaptability of the modified Lambert guidance routine, we make the actual trajectory deviate from the pre-designed one through increasing the thrust by 10 percent and decreasing the thrust by 10 percent for each case, respectively. The results shown in Table 5 suggest that the proposed modified guidance algorithm is almost insensitive to the trajectory deviations, and still has relatively high precision.
| Range | Thrust perturbation | Modified guidance algorithm | |
|---|---|---|---|
| (m) | (m) | ||
| Case 1 | Nominal | -18.0817 | -7.9047 |
| + 10% | -17.0677 | -7.8482 | |
| - 10% | -18.4369 | -7.9246 | |
| Case 2 | Nominal | -12.4436 | -2.6543 |
| + 10% | -11.6395 | -2.6131 | |
| - 10% | -13.2714 | -2.6969 | |
| Case 3 | Nominal | -6.5109 | -1.0116 |
| + 10% | -5.5859 | -0.9846 | |
| - 10% | -7.4261 | -1.0351 | |
Table 5: Simulation results for different thrust perturbation.
In this work, an analytical solution for state deviation prediction of missile’s motion perturbed by the J2 term is proposed. The differential equation of missile’s state deviation with true anomaly as the independent variable is built in the LVLH frame which moving with a nominal two-body orbit. The expression of J2 gravitational acceleration vector with respect to true anomaly is also obtained in the LVLH frame based on spherical trigonometry in order to derive the analytical solution of state deviation vector. This proposed analytical model is used for real-time predicting the impact deviation of missile in the Lambert guidance routine. Some simulations have been conducted in this paper to verify the accuracy of this analytical model and its effectiveness in the missile guidance applications. Simulation results imply that this proposed analytical state deviation prediction model has enough precision and efficiency and performs well in missile guidance applications.
This work was supported by the National Basic Research Program 973 of China (6132220301).
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.