Enzyme Engineering
Open Access
ISSN: 2329-6674
ISSN: 2329-6674
Review Article - (2013) Volume 2, Issue 2
Keywords: Evolution of BRN, Complex network, Network homeostasis, Dynamical analysis
Network analysis has been applied widely, providing a unifying language to describe disparate systems ranging from social interactions to power grids. The notion of complex networks has become more and more popular for research in physics, engineering, biology and even social sciences [1-6]. A network can be viewed as a graph consisting of nodes connected by edges according to certain rules, in which the nodes and edges typically represent some physical, biological or social entities and their relationships, respectively [7,8]. Graph representation has been applied in many fields of scientific studies. For example, the Internet is a complex network of routers and computers linked by various physical or wireless links; fads and ideas spread on the social network, whose nodes are human beings and whose edges represent various social relationships; the World Wide Web is an enormous virtual network of Web pages connected by hyperlinks. These systems represent just a few of the many examples that have recently prompted the scientific community to investigate the mechanisms that determine the topology of complex networks [9,10].
Systems biology aims at investigating cellular networks by combining experiments, mathematical modeling and computer simulations. One fundamental prerequisite for the construction of cell models is the analysis of metabolic and signaling networks. The description of such systems comprises both the network structure and the reaction kinetics: only if both are known, stationary states, time courses and responses to parameter changes can be computed. Complex network theory has also been employed in molecular biology, but so far the resulting networks have only been analyzed statically [11-17]. In this work, we present the dynamics of biochemical reaction network on the molecular-scale. The rest of this paper is organized as follows. Section 2 gives the background knowledge of biochemical reaction and presents the problem formulation. In section 3, the Biochemical Reaction Model (BRN) is proposed and the algorithm for the biochemical reaction network is presented. Section 4 contains the simulation results for the biochemical reaction network in the initial state and equilibrium state, and the analytical comparisons between the BRN model and the proposed model. Finally, conclusions are drawn in Section 5.
In this paper, we shall be concerned with the following general problem: N biochemical species or proteins are distributed randomly. Some species may have a higher probability to interact, while some other species may have a lower probability to interact. The interaction probability for any two biochemical species is determined by the distance between them, as well as their activities. The biochemical species will be re-arranged after their interaction. Given the original distribution of these biochemical species and the rules of evolution, what are the relationships among these biochemical species at any later time?
The concentration of species (protein) is an important index in biochemical reaction. In traditional literature, the concentration is defined as n/v. Here n is the amount of protein, which is always changing in biochemical reaction system, and V is the volume which is often fixed. In this model, we define the relative concentration of the protein i as
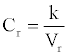 (1)
(1)
Where, k is a constant. We call Vr the relative interaction volume of protein A and B. Vr is defined as
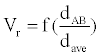 (2)
(2)
Where d(A, B) is the distance between protein A and B and dave the average distance. It is easy to find that the relative volume is varying, which will induce variation of protein concentration.
We demonstrate the evolution of the biochemical reaction system via simulation. Each node here indicates one biochemical species or protein. Two nodes are connected when they start to interact.
In this section, we propose the biochemical reaction network (BRN) model based on the random graph theory. We study the dynamics of the biochemical reaction network by analyzing the evolution of the average degrees and edges. The system equation describing the relationships among these proteins is given by
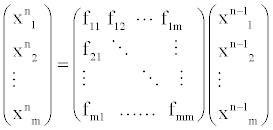 (3)
(3)
Where, xin denotes protein i in the n state and fij denotes the transfer function between protein i and j.
The evolution of the biochemical reaction network is governed by the following rules:
(1) Start with N isolated nodes that are distributed randomly.
(2) Calculate the interaction probability for any two biochemical species. The interaction probability can be expressed as
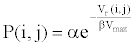 (4)
(4)
Where, α, β are biochemical parameters determined by the activity of biochemical species.
We define
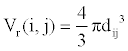 (5)
(5)
And
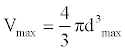 (6)
(6)
Where, dij indicates the distance between node i and node j. (1<=i<=N, 1<=j<=N). dmax indicates the maximum distance between node i and the origin of coordinates.
(3) Compare the interaction probability p (i,j) with r. If p(i, j)>=r, node i and node j is connected .
(4) Break the connection between node i and node j and reset the location of node i and j.
(5) Repeat step 2-4 until the equilibrium state of biochemical interaction system is achieved.
Prior to studying the topological properties of the biochemical reaction network, we briefly define the following feature parameters:
• Average node degree, denoted by
• Average clustering factor, denoted by
ss
• Average path length, denoted by
The biochemical reaction in real-world is a stochastic process. A new series of random numbers is needed to simulate the real biochemical reaction network. Figure 1 and 2 show the evolutions of the average degrees and edges, respectively.
The equilibrium states shown in Figure 1 and 3 demonstrate the real homeostasis in biochemical system. In the real biochemical system, the average degree and the edges always vary on a small-scale even if the system achieves homeostasis.
From Figure 1 and 2, we can find that the average degrees and edges are not increasing monotonically. Figure 3 can gives us a deeper insight into the evolution of the node degrees before the system reaches the equilibrium state. Figure 3 shows that the probability of high degrees, such as k=50, becomes larger and larger as the cycling numbers increases, which is in conformity with the conclusion of Figure 1 and 2. And this is also in accordance with performance of the biochemical reaction system in real world: as homeostasis is closer and closer, the interaction frequency becomes higher and higher.
Figure 4 shows the degree distribution in the initial state, while Figure 5 shows the corresponding degree distribution in the equilibrium state. The parameters used in the simulation are α=0.15, β=0.25, N=100.
In this section, the comparisons between the original random graph model and the proposed BRN model are given. Basic network features, namely, degree distribution, total number of edges, average node degree, average clustering factor and average shortest path, are examined respectively.
Table 1 shows the basic network features of the original random graph and BRN, respectively. From Table 1, we can find that BRN has lager average degree, clustering coefficient and edges than those of the original random graph. However, when it comes to the average path length, Things reverses. This demonstrates the superiority of biological evolution. Figure 6 and 7 show the probability distribution of degrees for the original random graph and BRN, respectively.
| α=0.12 β=0.22 | Original random graph | BRN (Initial state) | BRN (Homeostasis) |
| Total number of edges | 198 | 402 | 614 |
| Average node degree |
324 | 8.1 | 11.5 |
| Average clustering factor |
0.05604 | 0.083947 | 0.098671 |
| Average path length |
Inf | 2.6072 | 2.3841 |
| α=0.2 β=0.3 | Original random graph | BRN (Initial state) | BRN (Homeostasis) |
| Total number of edges | 452 | 586 | 831 |
| Average node degree |
8.42 | 11.32 | 16.53 |
| Average clustering factor |
0.0837 | 0.1295 | 0.1537 |
| Average path length |
2.3251 | 2.0594 | 1.7358 |
| α=0.38 β=0.28 | Original random graph | BRN (Initial state) | BRN (Homeostasis) |
| Total number of edges | 934 | 1451 | 1983 |
| Average node degree |
18.625 | 26.83 | 37.31 |
| Average path length |
1.6735 | 1.4831 | 1.2492 |
Table 1: Feature parameters of original random graph model and BRN model.
There are two recent developments in systems biology: first, biochemical networks can be easily extracted from databases; second, attempts are made to use this knowledge for large-scale or wholecell modeling without caring about individual reaction kinetics. To challenge these approaches, we attempted to extract information about biochemical network dynamics from the network structure, with very restricted knowledge about the individual reaction kinetics.
In this paper, The BRN model is proposed. The biochemical reaction system is studied using the random graph theory. The dynamics of the BRN is studied by analyzing the evolutions of some basic network features, such as average degrees and edges. The network features of BRN are demonstrated in both its initial state and equilibrium state. Furthermore, we compare the BRN with the original random graph by analyzing their network features. Our work provides a possible direction to study biochemical reaction system using complex network theory.