Journal of Theoretical & Computational Science
Open Access

Anomalous Thermodynamic Properties of Water and Water Molecules

Makoto Yasutomi^{* *}Correspondence: Makoto Yasutomi, Department of Physics and Earth Sciences, University of the Ryukyus, Nishihara-Cho, Okinawa, Japan, Email:

Author info »

Introduction

When the Pressure (P) is 1 atm and the Temperature (T) is 3.98°C or higher, water expands when heated and contracts when cooled (positive thermal expansion). However, at temperatures below 3.98°C, water contracts when heated and expands when cooled (negative thermal expansion). The measured values of the change in the water density (mρ) with temperature are shown as black circles in Figure 1. Here, m represents the mass of one water molecule and ρ represents the number of water molecules per unit volume (Figure 1).

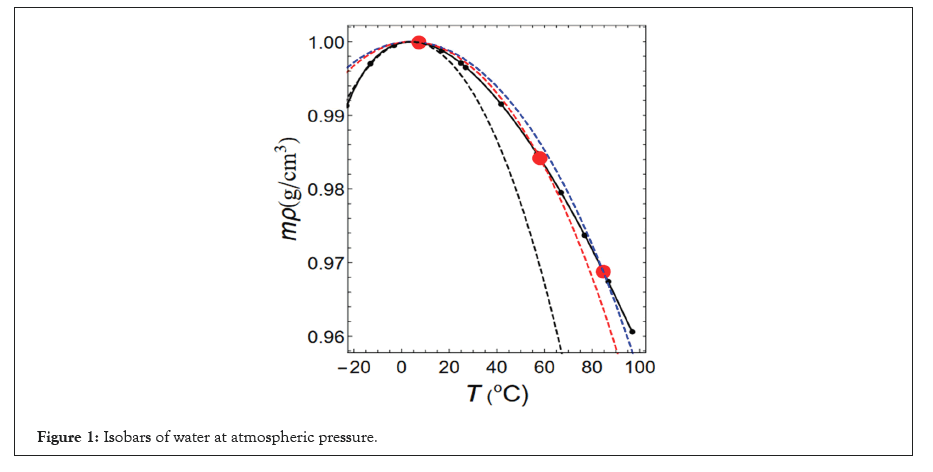
Figure 1: Isobars of water at atmospheric pressure.

The black circles indicate the experimental results [1]. The red circles represent the theoretical isobars obtained in this study. The solid black line represents measured value of mρ. The blue, red and black dashed lines represent isobars obtained by fixing the functional shape of the intermolecular interactions shown by the solid blue, red and black lines respectively.

The isothermal compressibility k is defined in Equation (1)

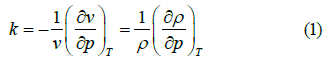
Where v denotes the volume of the system under consideration. The temperature dependence of k is shown in Figure 2, k reaches its minimum at approximately 46°C (Figure 2).

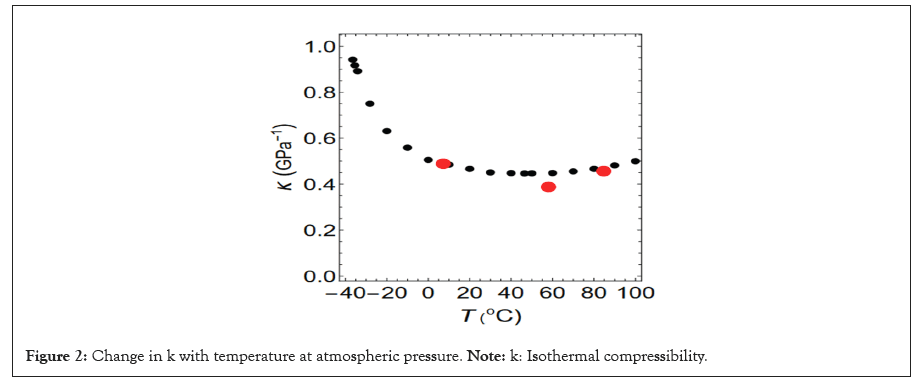
Figure 2: Change in k with temperature at atmospheric pressure. Note: k: Isothermal compressibility.

The black circles represent the experimental results [2]. The red circles indicate the theoretical results of this study.

Furthermore, the measured value of the isobaric specific heat c_p of water nearly remains constant at 4.2 J/(gK) in the temperature range 0<T (°C)<100.

Thermodynamic physical parameters, such as water density, isothermal compressibility and specific heat at constant pressure, exhibit unexplained changes with temperature. For centuries, numerous scientists have conducted research to elucidate the mechanisms by which such unusual phenomena occur and various theories have been proposed [3-18]. Although none of these theories have solved these issues, Yasutomi [19-22], recently solved the mystery of the unusual change in density with temperature by relating this change to the functional shape of the interactions between the water molecules. In this study, we identify intermolecular interactions that can reproduce the measured results of changes in specific heat at constant pressure and isothermal compressibility, in addition to density and temperature and explain the unusual thermal behavior of water. We show that these changes are caused by unusual thermodynamic properties of the molecule.

Unraveling the mystery of related phenomena in relation to the shape of the interactions between molecules has been a traditional and fundamental method in physics since Newton’s time.

Isobaric specific heat capacity and excess internal energy

The measured value of mρ shown in Figure 1 can be reproduced using the following Equation (2)

Here, the unit of T is degrees Celsius. In addition, (c₀,c₁-c₇)=(0.99984, 6.7403 × 10^-5, -9.0917 × 10^-6, 1.1429 × 10^-7, -2.1114 × 10^-9, 3.1712 × 10^-11, -2.6661 × 10^-13, 8.9058 × 10^-16).

The thermal expansion coefficient α_p is defined in Equation (3)

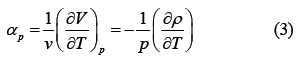
The results obtained by substituting Equation (2) into Equation (3) are shown in Figure 3.

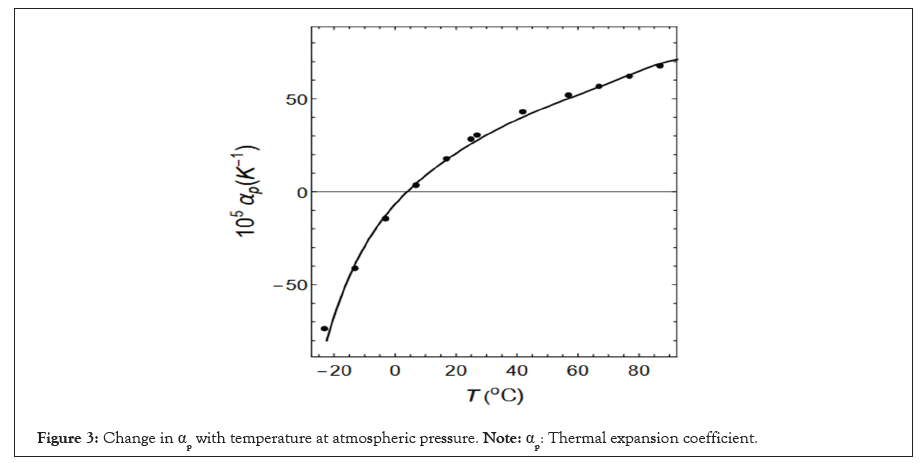
Figure 3: Change in α_p with temperature at atmospheric pressure. Note: α_p: Thermal expansion coefficient.

The black circles indicate the experimental results [1]. The solid line represents Equation (3). The potential energy u per unit volume of the system is called the excess internal energy and is expressed in Equation (4).

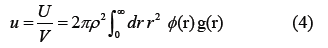
Here, U is the total potential energy of the system, g(r) is the two-body distribution function of the water molecules and ϕ(r) is the intermolecular interaction. The isobaric specific heat capacity c_p of water is expressed in Equation (5)

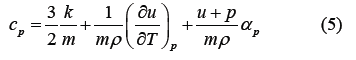
Where, k is Boltzmann’s constant. To calculate α_p in Equation (5), we use Equations (2) and (3), which are justified by the identification of the intermolecular interactions that can reproduce Equation (2) with high accuracy.

If we set c_p=4.2 J/(gK) and substitute Equation (3) into Equation (5), we obtain a first-order differential equation for u(T) with respect to T. If we solve this equation numerically, we obtain the u(T) indicated by the solid line. There are an infinite number of such u(T) curves because they contain an integration constant. However, we adopt u(0°C)=-2096.66 J/cm³. Therefore, we reproduce c_p(T)=4.2 J/(gK) and the u-T relationship shown by the solid line in Figure 4.

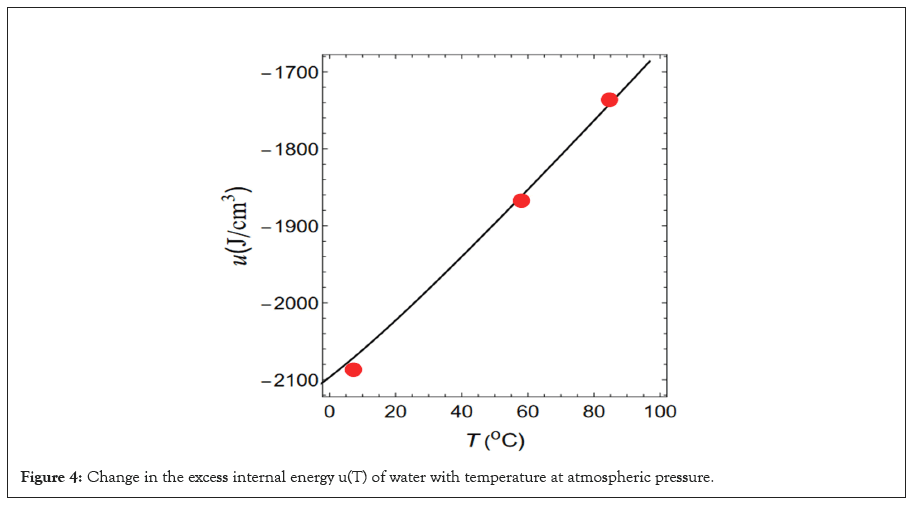
Figure 4: Change in the excess internal energy u(T) of water with temperature at atmospheric pressure.

In this study, we aimed to identify the interactions between the water molecules that reproduce the solid line in Figure 4 and the experimental results shown in Figures 1 and 2. Furthermore, we clarified the relationship between the functional shapes of the interactions and these thermodynamic phenomena. Therefore, a suitable water model must be developed.

Materials and Methods

Water model

Various thermodynamic physical quantities can be derived from the thermodynamic potential u defined in Equation (4). Because the relationship between u and ϕ(r) is clear compared to other thermodynamic potentials, our method is convenient for this type of research. ‘u’ can be obtained by numerically solving the following equation using the Self-Consistent Ornstein-Zernike Approximation (SCOZA) in Equation (6) [23-29].

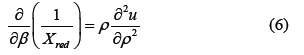
The red circles indicate the theoretical results of this study.

Here, β=1/kT and X_red is the reduced isothermal compressibility defined by the following Equation (7)

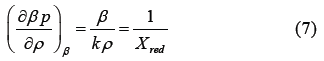
The intermolecular interaction ϕ(r) of water in thermal equilibrium comprises three parts: the hard-core potential, soft-repulsive tail and attractive tail and is expressed in Equation (8).

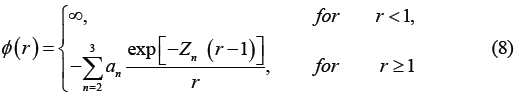
Here, a₂ is normalization constant with a potential depth of 1 and a₃/a₂, Z₂ and Z₃ are the free parameters. In addition, the hard core diameter (σ) is a unit of length and the potential depth (ε) is a unit of energy.

Results

Calculation method

If the thermal equilibrium state of water changes, then the structure, coordination and orientation of the water molecules and the shape of the electron wave function around each water molecule will change accordingly. Therefore, the functional shape of the interaction between water molecules constantly changes as the thermal equilibrium state changes. In this study, we considered these effects in our calculations.

In SCOZA, we performed calculations using water vapour in thermal equilibrium at atmospheric pressure and infinite temperature as the initial conditions and then gradually lowered the temperature.

Thermal equilibrium has been thermodynamically proven independent of the path through which it is achieved. Therefore, calculations can be performed using the functional form of fixed intermolecular interactions. At a certain temperature, if the experimental and theoretical values of the density and isothermal compressibility agree and if the theoretical value of the excess internal energy matches the u shown in Figure 4 by the solid line, then this intermolecular interaction can be considered to be the interaction between water molecules in a state of thermal equilibrium at that temperature.

Calculation results in the range of 0<T (°C)<100

The physical quantities that are reproduced are the changes in three quantities with temperature, density, isobaric heat capacity and isothermal compressibility. However, the measured values of the specific heat at constant pressure were only obtained for the temperature range 0<T (°C)<100; therefore, we discuss the thermodynamic phenomena within this temperature range.

The interaction between water molecules defined by Equation (8) includes four parameters (a₂, a₃ and Z₂, Z₃). However, because a₂ is normalization constant, the interaction is specified by a combination of the three remaining free parameters (a₃/a₂ and Z₂, Z₃) ∞³ combinations exist. We identified three sets of combinations that reproduced the experimental results. There were three temperature values, expressed in degrees Celsius: T₁=84.69, T₂=58.05 and T₃=7.25.

Z₂ and Z₃ with respect to temperature are listed in Table 1. The values of a₂, a₃/a₂, σ and ε are listed in Table 2. The tails of the intermolecular interactions with respect to the temperature T_j (j=1-3) are shown in Figure 5.

Table 1: Values of Z₂ and Z₃ with respect to Temperature (T).

Table 2: Values of a₂, a₃/a₂, (σ) and (ε) with respect to Temperature (T).

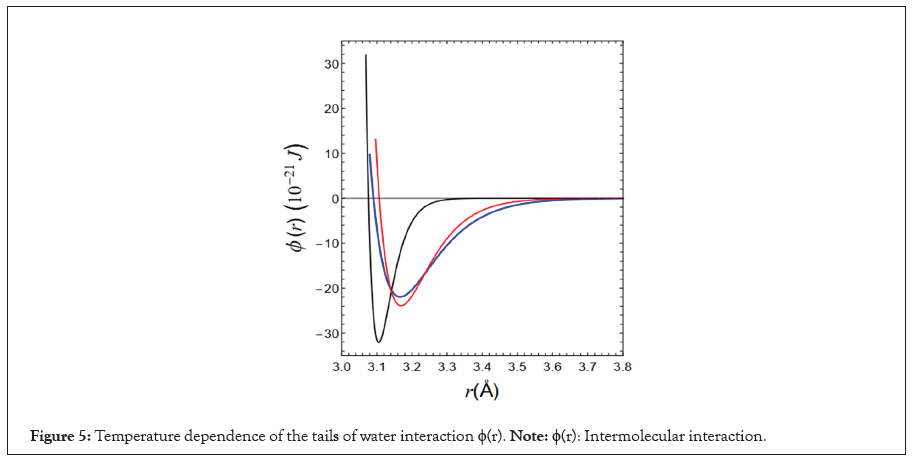
Figure 5: Temperature dependence of the tails of water interaction ϕ(r). Note: ϕ(r): Intermolecular interaction.

The tails of the three intermolecular interactions are indicated by blue, red and black lines in Figure 5. The isobars obtained by fixing the shapes of these functions are shown as blue, red and black dashed lines in Figure 1. The dashed lines indicate the maximum density. For the isobars, if we implement the condition that the theoretical and experimental maximum densities match at 1 atm and 3.98°C, then the values of the length-unit (σ) and the energy-unit (ε) are obtained from the following Equations (9-11) [23].

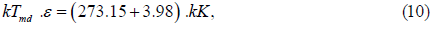
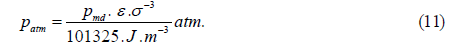
Where ρ_md is the theoretical value of the maximum density, T_md is the theoretical value of the temperature at the density and P_md is the theoretical value of the pressure at ρ=ρ_md and T=T_md. The values of ρ_md, T_md and P_md obtained from the three dashed isobars in Figure 1 are listed in Table 3.

Table 3: Values of P_md, ρ_md and T_md with respect to the theoretical isobars.

The theoretical isobar, shown as the blue dashed line in Figure 1 coincides with the experimental isobar, shown as a solid line, at the points of maximum density. The blue dashed line deviates from the solid line as the temperature increases, but it intersects the experimental isobar again at the red circle point T=T₁ shown at the right end of the figure. The same is true for the isobars indicated by the red and black lines, which intersect the experimental isobar at the red circle points T=T₂ and T=T₃, respectively. Therefore, the experimental and theoretical values of temperature and density determined by fixing the three intermolecular interactions relative to atmospheric pressure agree with high accuracy.

The excess internal energies obtained from these three interactions are indicated by red circles in Figure 4. As shown in the Figure 4 these models reproduce the excess internal energy indicated by the solid line with high accuracy. The process for reproducing the u(T) shown by this solid line is the same as that for reproducing the isobaric specific heat capacity of c_p=4.2 J/ (gK). However, when calculating α_p, ρ is assumed to change along the isobar indicated by the solid line in Figure 1 because the real water changes along the isobar shown as the solid line and not along the isobars shown as broken lines.

In addition, the isothermal compressibility k obtained for the three interactions mentioned above is indicated by red circles in Figure 2. The isothermal compressibility’s k (T₁) and k (T₃) obtained from the tails indicated by the blue and black dashed lines in Figure 5 reproduced the experimental values with high accuracy. However, k (T₂) obtained from the tail indicated by the red broken line does not agree well with the experimental value, although we believe that it is within the allowable range.

Figure 6 shows the radial distribution functions g(r) of the water molecules for each thermal equilibrium state at temperatures T₁-T₃.

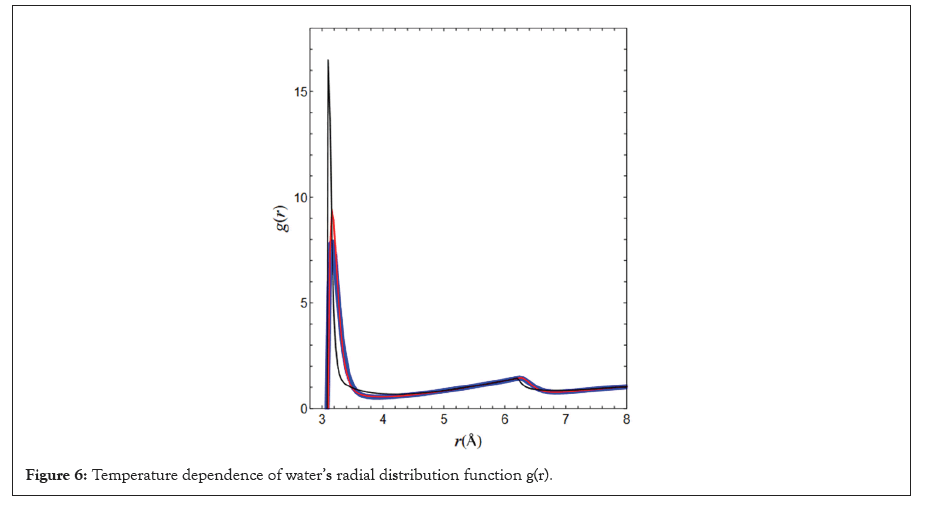
Figure 6: Temperature dependence of water’s radial distribution function g(r).

As the temperature decreased, the principal maximum of g(r) increased and the position r decreased monotonically, which is likely a reflection of the fact that in this temperature range, the density increases monotonically with decreasing temperature due to positive thermal expansion. Similarly, below 4°C, it is inferred that the principal maximum of g(r) decreased and the position r increased monotonically as the temperature is cooled because of the negative thermal expansion. From this temperature dependence of g(r), it is easy to understand the temperature dependence of the density, but it is difficult to elucidate the relationship between the isobaric specific heat and the thermal behaviour of isothermal compressibility. The author believes that the temperature dependence of intermolecular interactions is more important in unravelling the mysteries of the thermodynamic behaviour of water.

The results shown in Figure 6 do not seem to have very good reproducibility when compared to the actual measurements. However, considering the current general precision of liquid physics, we believe that our results are acceptable.

Discussion

Water exhibits mysterious thermodynamic properties. Numerous scientists have attempted to unravel this mystery and various theories have been proposed.

However, none of these theories have resolved this issue. Recently, the author of this paper solved the mystery of negative thermal expansion exhibited by water by relating this phenomenon to the functional shape of intermolecular interactions. Furthermore, in this study, we identified intermolecular interactions for three temperatures (T₁, T₂ and T₃)=(84.69, 58.05 and 7.25) that can reproduce the experimental results of changes in three thermodynamic quantities with temperature in the temperature range of 0<T (°C)<100, specific heat at constant pressure, isothermal compressibility and density. These three intermolecular interactions are shown in Figure 5.

In addition, the excess internal energy u(T) is indicated by red circles in Figure 4. These red circles reproduce the u-T relationship shown by the solid black line with high accuracy. The energy u(T) indicated by the solid black line is the excess internal energy, which yields c_p=4.2 (J/gK). However, there are countless other u(T) curves owing to their integration constant. The solid line in Figure 4 is an example. In addition, because of this indeterminacy, the functional shape of the intermolecular interactions shown in Figure 5 is not unique at a given temperature and numerous other shapes may exist. Therefore, in the future, we must devise a method to eliminate this uncertainty.

The change in density with temperature is indicated by the red circles in Figure 1 and the experimental values were reproduced with high accuracy. This justifies the use of Equation (2) when calculating α_p.

The change in isothermal compressibility with temperature is indicated by the red circles in Figure 2. The experimental values of k for 84.69°C and 7.25°C are accurately reproduced. However, although the reproducibility of k at 58.05°C cannot be considered highly accurate, we believe that it is within the acceptable range.

Conclusion

Currently, the amount of theoretical data is insufficient; therefore, we need to increase the amount of theoretical data to reproduce experimental values with high accuracy. However, the anomalous thermodynamic behavior of water is caused by complex changes in the interactions between the water molecules as the temperature changes. The same can be inferred from the thermodynamic properties of the ice. The experimental verification of these issues is strongly desired. Furthermore, interesting changes in the density and isothermal compressibility with temperature were experimentally obtained at temperatures below 0°C and to unravel the mystery of this behavior, measurements of the isobaric specific heat at temperatures below 0°C are required. In addition, researching the properties of liquids that do not exhibit negative thermal expansion, as in this study and comparing them with those of liquids that exhibit negative thermal expansion are important for understanding the thermodynamic properties of liquids as a whole. We also believe that by numerically calculating the changes in the electron wave function around water molecules with temperature, we will gain deeper knowledge about the temperature dependence of the intermolecular interactions.

References

1. Abascal JL, Vega C. A general purpose model for the condensed phases of water: TIP4P/2005. J Chem Phys. 2005;123(23):234505.

   [Crossref] [Google Scholar] [PubMed]

2. Chaplin M. Water structure and science.
3. Rontgen WC. Ueber die constitution des flüssigen wassers. Annalen der Physik. 1892;281(1):91-97.

   [Crossref] [Google Scholar]

4. Russo J, Tanaka H. Understanding water’s anomalies with locally favoured structures. Nat Commun. 2014;5(1):3556.

   [Crossref] [Google Scholar] [PubMed]

5. Fomin YD, Tsiok EN, Ryzhov VN. Inversion of sequence of diffusion and density anomalies in core-softened systems. J. Chem. Phys. 2011;135(23):234502.

   [Crossref] [Google Scholar] [PubMed]

6. Gribova NV, Fomin YD, Frenkel D, Ryzhov VN. Water like thermodynamic anomalies in a repulsive-shoulder potential system. Phys. Rev. E. 2009;79(5):051202.

   [Crossref] [Google Scholar] [PubMed]

7. Molinero V, Moore EB. Water modeled as an intermediate element between carbon and silicon. J Phys Chem B. 2009;113(13):4008-4016.

   [Crossref] [Google Scholar] [PubMed]

8. de Oliveira AB, Netz PA, Barbosa MC. An ubiquitous mechanism for water-like anomalies. EPL. 2009;85(3):36001.

   [Crossref] [Google Scholar]

9. Sadr-Lahijany MR, Scala A, Buldyrev SV, Stanley HE. Liquid-state anomalies and the stell-hemmer core-softened potential. Phys Rev Lett. 1998;81(22):4895.

   [Crossref] [Google Scholar]

10. Bernal JD, Fowler RH. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions. J. chem. Phys. 1933;1(8):515-548.

    [Crossref] [Google Scholar]

11. Pople JA. Molecular association in liquids II. A theory of the structure of water. Proc R Soc Lond Ser A Math Phys Sci. 1951;205(1081):163-178.

    [Crossref] [Google Scholar]

12. Pauling LI. The structure of water. In Hydrogen bonding. Pergamons. 1959:1-6.

    [Crossref] [Google Scholar]

13. Samoilov OY. A new approach to the study of hydration of ions in aqueous solutions. Discuss Faraday Soc. 1957; 24:141-146.

    [Crossref] [Google Scholar]

14. Meyer M, Stanley HE. Liquid-Liquid Phase Transition in Confined Water: A Monte Carlo Study. J Phys Chem B. 1999;103(44):9728-9730.

    [Crossref] [Google Scholar]

15. Mishima O, Stanley HE. Decompression-induced melting of ice IV and the liquid-liquid transition in water. Nature. 1998;392(6672):164-168. [Crossref]

    [Google Scholar]

16. Poole PH, Sciortino F, Essmann U, Stanley HE. Phase behaviour of metastable water. Nature. 1992;360(6402):324-328. [Crossref]

    [Google Scholar]

17. Sciortino F, La Nave E, Tartaglia P. Physics of the liquid-liquid critical point. Phys Rev Lett. 2003;91(15):155701.

    [Crossref] [Google Scholar] [PubMed]

18. Sun Z, Sun G, Chen Y, Xu L. Liquid-liquid phase transition in water. Sci China Phys Mech Astron. 2014;57:810-818. [Crossref]

    [Google Scholar]

19. Yasutomi M. Thermodynamic mechanism of the density and compressibility anomalies of water in the range- 30< T (° C)< 100. Sci Rep. 2022;12(1):1219.

    [Crossref] [Google Scholar] [PubMed]

20. Yasutomi M. Interparticle interactions between water molecules. Front Phys. 2014;2:64. [Crossref]

    [Google Scholar]

21. Yasutomi M. Thermodynamic mechanism of the density anomaly of liquid water. Front Phys. 2015;3:8. [Crossref]

    [Google Scholar]

22. Yasutomi M. Which shape characteristics of the intermolecular interaction of liquid water determine its compressibility? Front Phys. 2016;4:21. [Crossref]

    [Google Scholar]

23. Yasutomi M. The physics of liquid water. Jenny Stanford Publishing. 2021. [Crossref]

    [Google Scholar]

24. Betancourt-Cárdenas FF, Galicia-Luna LA, Benavides AL, Ramirez JA, Scholl-Paschinger E. Thermodynamics of a long-range triangle-well fluid. Molecular Physics. 2008;106(1):113-126. [Crossref]

    [Google Scholar]

25. Pini D, Stell G, Wilding NB. A liquid-state theory that remains successful in the critical region. Molecular Physics. 1998; 95(3):483-494. [Crossref]

    [Google Scholar]

26. Pini D, Stell G, Dickman R. Thermodynamically self-consistent theory of structure for three-dimensional lattice gases. Phys Rev E. 1998;57(3):2862. [Crossref]

    [Google Scholar]

27. Scholl-Paschinger E. Self-consistent Ornstein-Zernike approximation for the Sogami-Ise fluid. J Chem Phys. 2004;120(24):11698-11711. [Crossref]

    [Google Scholar] [PubMed]

28. Scholl-Paschinger E, Benavides AL, Castaneda-Priego R. Vapor-liquid equilibrium and critical behavior of the square-well fluid of variable range: A theoretical study. The J Chem Phys. 2005;123(23).

    [Crossref] [Google Scholar] [PubMed]

29. Yasutomi M. A self-consistent Ornstein-Zernike approximation for a fluid with a screened power series interaction. J Chem Phys. 2010;133(15):154115.

    [Crossref] [Google Scholar] [PubMed]