Journal of Developing Drugs
Open Access
ISSN: 2329-6631
ISSN: 2329-6631
Research Article - (2017) Volume 6, Issue 2
The aim of present work is to determine and analyse the kinetics of drug release from the matrix tablet by employing various mathematical models. A study was done with Carbidopa and Levodopa ER tablets, 50 mg/200 mg by employing wet granulation technique using Hydroxypropyl methylcellulose and Hydroxypropyl cellulose as matrix forming polymer. The in-vitro drug release profile was carried out in 0.1 N HCl (900 mL) using USP dissolution apparatus II (Paddle) at 50 rpm at an extended time period of 0.5, 0.75, 1, 1.5, 2, 2.5, 3 and 4 hours. The drug release data was obtained, quantitatively correlated and interpreted with various mathematical models viz. Zero order model, first order model, Higuchi model, Hixson-Crowell model and Korsmeyer-Peppas model and evaluated to understand the kinetics of drug release. The criterion for the most suitable model was based on the high degree of coefficient of correlation of drug release profile of Carbidopa Levodopa ER Tablet. Hence, finally concluded as the drug release pattern of Carbidopa Levodopa ER Tablets, 50 mg/200 mg was best fitted with Higuchi square root model and follows Higuchi drug release kinetics which is diffusion controlled.
<Keywords: Dissolution; Diffusion; Coefficient of correlation; Kinetics of drug release
Dissolution
When solid particles come in contact with the GI tract, a saturated layer of drug solution is created very quickly in the surface of particles in the liquid immediately surrounding them (called the diffusion layer). The drug molecules then diffuse through the GI content to the lipoidal membrane where diffusion across the gastro intestinal membrane and absorption into the circulation takes place [1].
There are two possible scenarios for the drug dissolution [1].
1. Absorption from solution takes place following the rapid dissolution of solid particles. In this case rate of absorption is controlled by rate of diffusion into the GI fluid.
2. Absorption from solution takes place following the slow dissolution of solid particles. In this case rate of absorption is controlled by rate of dissolution into the GI fluid.
Hence, Dissolution is a process in which a solid substance solubilises in a given solvent i.e., mass transfer from solid surface to the liquid phase [2].
Theories of drug dissolution: Several theories have been proposed to explain drug dissolution. Some of the important ones are:
• Diffusion layer model/ film theory.
• Danckwert model/ penetration or surface renewal theory.
• Interfacial barrier model/ double barrier or limited salvation theory.
Explanation of theories
Diffusion layer model/ film theory: This model considers that a layer of liquid, H cm thickness, close to the solid surface remains stagnant as the bulk liquid passes over the surface with a particular speed (Figure 1). The interaction at the solid/liquid interface is considered to be spontaneously formation of a saturated solution, CS, of the solid in the stagnant liquid layer. The rate of dissolution is carried out by the diffusion of the solid molecules from the stagnant liquid film to the bulk liquid according to Fick’s first law:
J=- Df dc/dx
where J is the amount of substance passing perpendicularly through a unit surface area per time, Df is the diffusion coefficient and dc/dx, is the concentration gradient. After a time t, the concentration between the limit of the stagnant liquid layer and the bulk liquid becomes Ct. Once the solid molecules pass into the bulk liquid, it is considered that there is rapid mixing and the concentration gradient disappears
This theory explains that a uniform rate of dissolution can be obtained if the concentration gradient is always constant i.e., CS-Ct is constant as CS>>Ct (as in “sink” conditions which generally mean CS>10 Ct).
Danckwert model/ penetration or surface renewal theory: This model considers that there is formation of macroscopic packets of solvent which attaches at the solid /liquid interface in adiffusion manner (Figure 2). Hence at the interface, the packet is able to absorb solute according to the laws of diffusion which is to be replaced by a new packet of solvent. This surface renewal process is related to the rate of transfer of solute and finally to the rate of dissolution. Though the diffusion layer model is the most commonly used, various alterations have been proposed. The current views of the diffusion layer model are based on the so-called effective diffusion boundary layer, the structure of which is heavily dependent on the hydrodynamic conditions. Aguiar et al. represented a theory which holds that dissolution occurs only when the drug is in small particles. Wagner altered above theory and showed that dissolution occurs from both the intact tablet and the aggregates and/or granules produced after disintegration.
Interfacial barrier model/ double barrier or limited salvation theory: In this model, it can be considered that the interaction at the solid/liquid interface is not spontaneous due to a high activation free energy barrier which is to be surrounded before the solid can dissolve (Figure 3). Thus, the dissolution mechanism is almost same as in diffusion layer model, with the concentration at the limit of the stagnant layer of liquid becoming Ct after time t. The rate of diffusion in the stagnant layer is relatively fast in comparison with the presence of the energy barrier, hence it becomes rate limiting in the dissolution process.
Basics of kinetics of drug release
Laws in the kinetics of drug release
Noyes-Whitney law [2]: Noyes-Whitney developed the fundamental principle of evaluation of drug release, which explains as
dC/dt=K (CS-Ct)
Where dC/dt is dissolution rate of drug,
K is dissolution rate constant,
Cs is the concentration of drug in the stagnant layer (also called as the saturation or maximum drug solubility),
Ct is the concentration of the drug in the bulk of the solution at time t.
Ficks law of diffusion[2]: According to this law drug molecules diffuse from a region of higher concentration to one of lower concentration until equilibrium is attained and that the rate of diffusion is directly proportional to concentration gradient across the membrane.
This can be expressed mathematically as
dQ/dt=DAKm/w(CGIT- C)/h
Where dQ/dt is rate of drug diffusion, amount per time (rate of appreance of drug in blood),
D is the diffusion coefficient. Its dimension is area per unit time, so typical units for expressing it would be m2/s (area/time),
A is the surface area for absorbing membrane for drug diffusion (area),
Km/w Partition coefficient of drug between lipoidal membrane and aqueous GI fluid (no unit),
CGIT- C is the difference in the concentration of drug in the GI fluid and the plasma called concentration gradient (amount per volume),
h is the thickness of the membrane (length).
Formulation of Carbidopa-Levodopa ER tablets, 50 mg/200 mg [3]
The Carbidopa and Levodopa combination is used to treat the symptoms of Parkinson′s disease, which is characterised by abnormally low levels of dopamine. Dopamine is a neurotransmitter which controls the skeletal muscular system. Patients suffering from Parkinson′s disease frequently have periods in which their mobility becomes difficult resulting inability to move.
Administering dopamine is not effective to treat Parkinson′s disease because dopamine dose not cross the blood brain barrier. To resolve this failure, Parkinson′s patients are administered Levodopa the metabolic precursor of dopamine. Levodopa crosses blood brain barrier and rapidly converted into dopamine and eradicating the symptoms of Parkinson′s disease caused by reduced level of dopamine. Levodopa is problematic because of its rapid decarboxylation by tissues other than the brain. Thus, when levodopa is administered alone, large doses are required because only small portion is transferred to brain unchanged.
Hence an aromatic amino-acid decarboxylase inhibitor such as Carbidopa can be used in combination with levodopa. Carbidopa inhibits the decarboxylation of Levodopa in the body tissue outside the brain. Hence, small doses of carbidopa can be administered in combination with levodopa which allow larger amount of levodopa to reach which later converted to dopamine which finally shows its efficacy. The carbidopa and levodopa combination product now available in immediate release as well as controlled release formulations. Controlled release formulations allow for the continuous release of the drug in an extended or prolonged period of time to maintain plasma levodopa concentration range.
In the present study, an attempt was made to design Carbidopa and Levodopa ER Tablet and its release profile was interpreted with various mathematical models [4].
• Zero order model
• First order model
• Higuchi model
• Korsmeyer -Peppas model
• Hixson-Crowell model
Materials
Carbidopa was procured from Zhejian Chiral medicine chemicals co. Ltd and Levodopa was procured from Divis laboratory Pvt. Ltd. Hydroxypropyl methylcellulose was purchaged from DOW Chemical Pacific Limited. and Hydroxypropyl cellulose was purchased from Ashaland Speciality Ingredients. Ferric oxide red from Sensient colors UK Ltd., Indigo caramine aluminium lake, Colloidal silicon dioxide was from Evonik speciality chemicals (Shanghai), Talc was from Imerys Talc from Italy and Magnesium stearate was received from Peter Greven, China. All other chemicals and ingredients used in the study were of analytical grade.
Methods
Preparation of Carbidopa-Levodopa ER tablets by wet granulation method: A prototype of formulation was designed by gathering the information from literatures and patents. The formulations were developed by wet granulation technique from a initial tentative formula to improved final formula (Table 1).
| S. No. | Name of Ingredient | F1 (%) | F2 (%) | F3 (%) | F4 (%) |
|---|---|---|---|---|---|
| 1 | Carbidopa | 16.67 | 16.67 | 16.67 | 16.67 |
| 2 | Levodopa | 66.67 | 66.67 | 66.67 | 66.67 |
| 3 | Hydroxypropyl methyl cellulose | 8.66 | 7.95 | 7.65 | 7.40 |
| 4 | Hydroxypropyl cellulose | 6.59 | 5.55 | 4.35 | 4.10 |
| 5 | Ferric oxide red | 0.02 | 0.02 | 0.02 | 0.02 |
| 6 | Indigo carmine aluminum lake | 0.14 | 0.14 | 0.14 | 0.14 |
| 7 | Colloidal silicon dioxide | 0.00 | 1.50 | 2.50 | 2.25 |
| 8 | Talc | 0.00 | 0.00 | 0.00 | 0.50 |
| 9 | Magnesium stearate | 1.25 | 1.50 | 2.00 | 2.25 |
| Total | 100.00 | 100.00 | 100.00 | 100.00 | |
| Observation | Picking sticking problem while compression | Picking sticking problem while compression | Picking sticking problem while compression | Final optimised formulation | |
Table 1: Formulation Details of Carbidopa-Levodopa ER Tablets, 50 mg/200 mg.
All the ingredients were sifted through #40 mesh separately except Ferric oxide red, Indigo caramine Aluminium Lake which were shifted through #80 mesh. Above ingredients were mixed in rapid mixer granulator for 5 minutes at a suitable speed of impeller and chopper to achieve uniform blend. Then granulation was done by adding water at a suitable speed of impeller and chopper for 5-6 minutes to achieve suitable granules. Drying of granules was carried out by fluid bed processor 60-70°C until to achieve LOD NMT 2%. Dried granules were milled by Comill having 0.8 mm screen. Finally, dried granules were lubricated with magnesium stearate and the lubricated blend was compressed into tablets using 12.7 × 7.5 mm oval shaped standard concave punches on a Minirotary tablet compression machine. The compression force was adjusted to achieve tablets having hardness in the range of 70-100 N and average weight of 300 mg.
From the above formulation, formulation F4 was considered as final optimised formulation and was selected for further study for the drug release profile and its release kinetics by the application of mathematical models.
Dissolution profile of Carbidopa Levodopa ER tablets: The invitro drug release profile was carried out in 0.1 N HCl (900 mL) at 37 ± 0.5°C using USP dissolution apparatus II (Paddle) at 50 RPM at an extended time period of 0.5, 0.75, 1, 1.5, 2, 2.5, 3 and 4 hours. Sample aliquots (5 mL) were withdrawn at 0.5, 0.75, 1, 1.5, 2, 2.5, 3 and 4 hours and replaced with equal volumes of fresh dissolution medium. Samples were suitably diluted, analysed by HPLC method and drug release was estimated.
Application of drug release data on mathematical models: Several mathematical equations which generally define the dissolution profile. Once an appropriate function has been selected, the evaluation of dissolution profile can be carried out and hence the drug release profile can be correlated with drug release kinetic models. Various mathematical models are employed to understand drug release kinetics which is explained below.
Zero order model [5]: According to the principles of pharmacokinetics, drug release from the dosage form can be represented by the equation:
C0-Ct =K0t
Ct=C0 +K0t
Ct is the amount of drug released at time t,
C0 is the initial concentration of drug at time t=0,
K0 is the zero-order rate constant.
Thus, zero order kinetics defines the process of constant drug release from a drug delivery system and drug level in the blood remains constant throughout the delivery.
Hence to study the drug release kinetics data obtained from in-vitro dissolution study is plotted against time i.e., cumulative drug release vs. time.
Hence the slope of the above plot gives the zero-order rate constant and the correlation coefficient of the above plot will give the information whether the drug release follows zero order kinetics or not.
Thus, this model was applied in the release profile of Carbidopa and Levodopa ER tablets, 50 mg/200 mg (Table 2) and evaluation was done in the graphical presentation (Figures 4 and 5).
| Time (Hr) | Cumulative % drug release (Carbidopa) | Cumulative % drug release (Levodopa) |
|---|---|---|
| 0.0 | 0 | 0 |
| 0.5 | 30 | 28 |
| 0.8 | 41 | 39 |
| 1.0 | 44 | 48 |
| 1.5 | 56 | 61 |
| 2.0 | 67 | 70 |
| 2.5 | 77 | 79 |
| 3.0 | 84 | 87 |
| 4.0 | 99 | 98 |
Table 2: Drug release profile of Carbidopa and Levodopa ER tablets, 50 mg/200 mg.
Observation: The graphical representation of cumulative % of drug release against time describes that drug release of Carbidopa and Levodopa from the matrix does not follow perfectly the principle of zero order release kinetics, though it is slightly approaching (r2=0. 933 for Carbidopa and r2=0. 0.9157 for Levodopa).
First order model [5]: The release of drug which follows first order kinetics can be represented by the equation
DC/dt=-K1C
K1 is the first order rate constant, expressed in time-1 or per hour.
Hence it can be defined as that first order process is the one whose rate is directly proportional to the concentration of drug undergoing reaction i.e., greater the concentration faster the reaction. Hence, it follows linear kinetics.
After rearranging and integrating the equation,
log C=log C0-K1t/2.303
K1 is the first order rate equation expressed in time-1 or per hour,
C0 is the initial concentration of the drug,
C is the percent of drug remaining at time t.
Hence to study the drug release kinetics data obtained from in-vitro dissolution study is plotted against time i.e., log % of drug remaining vs. time and the slope of the plot gives the first order rate constant. The correlation coefficient of the above plot will give the information whether the drug release follows first order kinetics or not.
Thus, this model was applied in the release profile of Carbidopa and Levodopa ER tablets, 50 mg/200 mg (log Cumulative % drug remaining vs. time refer Table 3) and evaluation was done in the graphical presentation (Figures 6 and 7).
| Time (Hr) | log Cumulative % drug remaining (Carbidopa) | log Cumulative % drug remaining (Levodopa) |
|---|---|---|
| 0.0 | 2.000 | 2.000 |
| 0.5 | 1.845 | 1.857 |
| 0.8 | 1.771 | 1.785 |
| 1.0 | 1.748 | 1.716 |
| 1.5 | 1.643 | 1.591 |
| 2.0 | 1.519 | 1.477 |
| 2.5 | 1.362 | 1.322 |
| 3.0 | 1.204 | 1.114 |
| 4.0 | 0.000 | 0.301 |
Table 3: Drug release profile (log Cumulative % drug remainining) of Carbidopa and Levodopa ER tablets, 50 mg/200 mg.
Observation: The graphical representation of cumulative % of drug release against time describes that drug release of Carbidopa and Levodopa from the matrix does not follow the principle of first order release kinetics as there is lower value of coefficient of correlation (r2=0.8322 for Carbidopa and r2=0.9212 for Levodopa).
Higuchi model [6]: The release of a drug from a drug delivery system (DDS) involves both dissolution and diffusion. Several mathematical equations models describe drug dissolution and/or release from DDS. In the modern era of controlled-release oral formulations, ‘Higuchi equation’ has become a prominent kinetic equation in its own right, as evidenced by employing drug dissolution studies that are recognized as an important element in drug delivery development. Today the Higuchi equation is considered one of the widely used and the most well-known controlled-release equation.
The classical basic Higuchi equation is represented by

where Q is the cumulative amount of drug released in time t per unit area, CO is the initial drug concentration, CS is the drug solubility in the matrix and D is the diffusion coefficient of the drug molecule in the matrix.
This relation is valid until total depletion of the drug in the dosage form is achieved. To study the dissolution from a planar heterogeneous matrix system, where the drug concentration in the matrix is lower than its solubility and the release occurs through porous system, the expression can be given by equation [5].
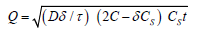
where D is the diffusion coefficient of the drug molecule in the solvent; δ is the porosity of the matrix; τ is the tortuisity of the matrix and Q, A, Cs and t have the meaning described above.
Tortuisity is defined as the dimensions of radius and branching of the pores and canals in the matrix. After simplifying the above equation, Higuchi equation can be represented in the simplified form
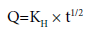
where, KH is the Higuchi dissolution constant.
The data obtained were plotted as cumulative percentage drug release versus square root of time. Therefore, the simple Higuchi model will result a linear Q versus t1/2 plot having gradient, or slope, equal to KH and we say the matrix follows t1/2 kinetics.
Hence if the correlation coefficient is higher for the above plot then we can interpret that the prime mechanism of drug release is diffusion controlled release mechanism.
It is important to note that a few assumptions are made in this Higuchi model. These assumptions are:
(i) the initial drug concentration in the system is much higher than the matrix solubility
(ii) Perfect sink conditions are maintained
(iii) The diffusivity of the drug is constant and
(iv) The swelling of the polymer is negligible. The sink conditions are achieved by ensuring the concentration of the released drug in the release medium never reaches more than 10 per cent of its saturation solubility.
Thus, this model was applied in the release profile of Carbidopa and Levodopa ER tablets, 50 mg/200 mg (Cumulative % drug release vs. Square root time refer Table 4) and evaluation was done in the graphical presentation (Figures 8 and 9).
| Time (Hr) | Square root time (Hr) | Cumulative% drug release (Carbidopa) | Cumulative% drug release (Levodopa) |
|---|---|---|---|
| 0.0 | 0.000 | 0 | 0 |
| 0.5 | 0.707 | 30 | 28 |
| 0.8 | 0.866 | 41 | 39 |
| 1.0 | 1.000 | 44 | 48 |
| 1.5 | 1.225 | 56 | 61 |
| 2.0 | 1.414 | 67 | 70 |
| 2.5 | 1.581 | 77 | 79 |
| 3.0 | 1.732 | 84 | 87 |
| 4.0 | 2.000 | 99 | 98 |
Table 4: Drug release profile (Cumulative% drug remaining) of Carbidopa and Levodopa ER tablets, 50 mg/200 mg.
Observation: The graphical representation of cumulative % of drug release against time represents that drug release of Carbidopa and Levodopa from the matrix is perfectly following Higuchi drug release model as the drug release profile is very closest to trend line or regression line and there is highest value of coefficient of correlation (r2= 0.9931 for Carbidopa and r2=0.9916 for Levodopa).
Korsmeyer-peppas model [7]: Once it has been ascertained that the prime mechanism of drug release is diffusion controlled from Higuchi plot then it comes the release of drug follows which type of diffusion.
To understand the dissolution mechanisms from the matrix, the release data were fitted using the well-known empirical equation proposed by Korsmeyer and Peppas.
Korsmeyer and Peppas put forth a simple relationship which described the drug release from a polymeric system follow which typeof dissolution and he represented a equation as:
Mt/M∞=Kkptn
Mt/M∞ is a fraction of drug released at time t,
log(Mt/M∞)=log Kkp+nlog t,
Mt is the amount of drug released in time t,
M∞ is the amount of drug released after time ∞,
n is the diffusional exponent or drug release exponent,
Kkp is the Korsmeyer release rate constant.
To study release kinetics a graph is plotted between log cummulative % drug release log(Mt/M∞) vs. log time (log t).
Hence, n value is used to characterize different release mechanisms as given in tabular form (Table 5) for cylindrical shaped matrices. Thus, this model was applied in the release profile of Carbidopa and Levodopa ER tablets, 50 mg/200 mg (log Cumulative % drug released vs. log time, Table 6) and evaluation was done in the graphical presentation (Figures 10 and 11).
| Release exponent (n) | Drug transport mechanism | Rate as a function of time |
|---|---|---|
| 0.5 | Fickian diffusion | t-0.5 |
| 0.45 |
Non -Fickian transport | tn-1 |
| 0.89 | Case II transport | Zero order release |
| Higher than 0.89 | Super case II transport | tn-1 |
Table 5: Different release mechanisms.
| log time | log Cumulative% drug released (Carbidopa) | log Cumulative% drug released (Levodopa) |
|---|---|---|
| 0.000 | 0.000 | 0.000 |
| -0.301 | 1.477 | 1.447 |
| -0.125 | 1.613 | 1.591 |
| 0.000 | 1.643 | 1.681 |
| 0.176 | 1.748 | 1.785 |
| 0.301 | 1.826 | 1.845 |
| 0.398 | 1.886 | 1.898 |
| 0.477 | 1.924 | 1.940 |
| 0.602 | 1.996 | 1.987 |
Table 6: Drug release profile (log Cumulative% drug releasedvs.log time) of Carbidopa and Levodopa ER tablets, 50 mg/200 mg.
Observation: From the above figures (Figures 10 and 11) the slope of the plot was constructed which described that the release exponent or the diffusion exponent found to be higher than 0.89 which implies that the drug release from the system follow Super case II transport [8].
Hixson-crowell model [7]: The Hixson-Crowell cube root law describes the release from systems where there is a change in surface area and diameter of particles or tablets. Hence, particles of regular area are proportional to the cube root of its volume. From the above concept Hixson-Crowell established a relationship between drug release and time which can be represented by equation as
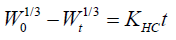
where W0 is the initial amount of drug in the pharmaceutical dosage form (Amount of drug remaining at time 0)
Wt is the remaining amount of drug in the pharmaceutical dosage form at time t; KHC is the Hixson-Crowell constant describing surface volume relation.
To study the release kinetics a graph is plotted between cube root of drug percentage remaining in matrix versus time.
This equation is used for interpretation of dissolution data of conventional dosage form, dispersible dosage form or immediate release dosage form. Hence, if the correlation coefficient of the above equation is higher, then we can interpret that change in surface area during the process of dissolution has a significant effect on drug release.
Thus, this model was applied in the release profile of Carbidopa and Levodopa ER tablets, 50 mg/200 mg (cube root of drug percentage remaining vs. time refer Table 7) and evaluation was done in the graphical presentation (Figures 12 and 13).
| Time (Hr) | Cube root of (Wo-Wt) (Carbidopa) | Cube root of (Wo-Wt) (Levodopa) |
|---|---|---|
| 0.0 | 0.000 | 0.000 |
| 0.5 | 0.521 | 0.482 |
| 0.8 | 0.749 | 0.706 |
| 1.0 | 0.816 | 0.909 |
| 1.5 | 1.112 | 1.251 |
| 2.0 | 1.434 | 1.535 |
| 2.5 | 1.789 | 1.883 |
| 3.0 | 2.122 | 2.291 |
| 4.0 | 3.642 | 3.382 |
Table 7: Drug release profile (cuberootof drugpercentageremainingvs.time) of Carbidopa and Levodopa ER tablets, 50 mg/200 mg.
Observation: From the above figures (Figures 12 and 13) it was predicted that change in surface area and diameter of the tablets with the progressive dissolution of matrix as a function of time [9].
The in-vitro drug release profile was applied in different mathematical models and was interpreted in the form of graphical presentation and evaluated by correlation coefficient (r2) represented in Table 8. The highest degree of correlation coefficient determines the suitable mathematical model that follows drug release kinetics [10].
| Model Name | Carbidopa | Levodopa | ||||
|---|---|---|---|---|---|---|
| r2 | Slope | Intercept | r2 | Slope | Intercept | |
| Zero order model | 0.933 | 22.59 | 17.04 | 0.9157 | 22.942 | 17.792 |
| First order model | 0.8322 | -0.4206 | 2.1673 | 0.9212 | -0.3808 | 2.1079 |
| Higuchi model | 0.9931 | 47.823 | 0.000 | 0.9916 | 48.976 | 0.0000 |
| Korsmeyer -Peppas model | -4.156 | 3.1562 | 0.000 | -4.09 | 3.1875 | 0.0000 |
| Hixson-Crowell model | 0.9586 | 0.8122 | 0.0213 | 0.9897 | 0.7911 | 0.0416 |
Table 8: External Factors Evaluation (EFE) matrix analysis.
From the above comparison, it was found that Higuchi square root model showed higher degree of correlation coefficient (r2) than other models. Hence, drug release profile of Carbidopa and Levodopa ER Tablets, 50 mg/200 mg follows diffusion mechanism.
Also, the model Korsmeyer-Peppas power law equation states the type of diffusion, which was evaluated by value, n which is higher than 0.89 which implies that the drug release from the system follow Super case II transport [11].
Mathematical models play a vital role in the interpretation of mechanism of drug release from a dosage form. It is an important tool to understand the drug release kinetics of a dosage form. The matrix tablets of Carbidopa-Levodopa 50 mg/200 mg were manufactured in this research paper showed an extended release profile with the polymers Hydroxy propyl methyl cellulose and Hydroxy propyl cellulose. The drug release was found to be best fitted by Higuchi square root model (r2=0.9931 for Carbidopa and r2=0.9916 for Levodopa) which implies that release of drug from matrix as a square root of time dependent process and diffusion controlled. The dissolution data was also plotted according to Hixson –Crowell model (r2=0.958 for Carbidopa and r2=0.989 for Levodopa) which describes that change in surface area and diameter of the tablets with the progressive dissolution of matrix as a function of time. Also, the model Korsmeyer-Peppas power law equation states the type of diffusion, which was evaluated by value, n (Release exponent) which is higher than 0.89 which implies that the drug release from the system follow Super case II transport.
We are heartily thankful and extremely gratified to formulation development department and fellow colleagues of Beijing Sciecure Pharmaceuticals Co., Ltd., for helping us in the technical aspects of the projects and also useful scientific discussions to carry out our research work successful.