International Journal of School and Cognitive Psychology
Open Access
ISSN: 2469-9837
+44 1478 350008
ISSN: 2469-9837
+44 1478 350008
Research - (2023)Volume 10, Issue 1
We mimic the cognitive ability of Human perception, based on Bayesian hypothesis, to recognize view-based 3D objects. We consider approximate Bayesian (Empirical Bayesian) for perceptual inference for recognition. We essentially handle computation with perception. Recent development in neuroscience indicates human perception can be represented by Bayesian inference. Bayesian models can perform variety of perceptual task; thus we should have an instrumentalist view towards Bayesian models in the context of neuroscience. Bayesian models are very effective to secure both subjects’ perceptual activity and capture features of the human neural mechanism. Bayesian model can be used to study brain’s various perceptual tasks. In this design study to represent the perceptual task in Bayesian approach we consider beta distribution for computation of prior, like-lihood and posterior probability. Due to the computational simplicity we consider beta distribution as stated above. The basic aim of this article is to demonstrate that computation with perception is Bayesian inference and essentially we express the perception as an optimal hypothesis in terms of resulting belief obtained from sensory data (likelihood data). Recently Bayesian approach achieved tremendous success in the field of computer vision. Thus it leads to model human visual perception and allows an observer to perceive the world.
Bayesian brain; Perception; Approximate Bayesian; Empirical Bayesian; View based 3D objects
This paper deals with the concept of approximate Bayesian (Empirical Bayesian) for perceptual inference to recognize view based 3D objects which are projected as 2D images. Views are characterized by two attributes; view likelihood and view stability.
View likelihood is the probability of a certain view of a given 3D object observed as 2D image which is an aspect of the given 3D object from a particular viewing direction. View stability indicates what extent image changes if the viewing direction is slightly changed: It is the generic view. Both the phenomena are identical up to the prior probability of camera orientation and can be used to compare images.
A large number of psychological research is found on the role of aspect in object recognition. Koenderink and van Doorn [1,2]. First considered this idea of aspects of a 3D object Tarr and Kriegman [3]. Performed research on the definition of view in the context of hu-man perception. This lends credence to the theory of using views as the basis for object recognition.
The Bayesian brain hypothesis
As proposed the Bayesian brain hypothesis is a probability based concept to generate the cognitive ability of perception as a generative model [4]. Based on the concept that the brain has a model of the world using sensory inputs [5] we try to mimic the cognitive ability of human perception for recognising 3D objects.
The brain is an inference machine that generates optimal hypothesis which can be viewed as posterior probability (belief about the world given the sensed data) and which can be represented by the product between likelihood of the sensed data of the given world and a prior (past experience about the world) [6]. Perception which is expressed as best hypothesis becomes the posterior probability which maps the perceived data into the belief about the world. (Figure 1) depicts the above mentioned concept of computation with perception. Human perception is full of uncertainty. Hence it is represented by probabilistic approach to Bayesian hypothesis.
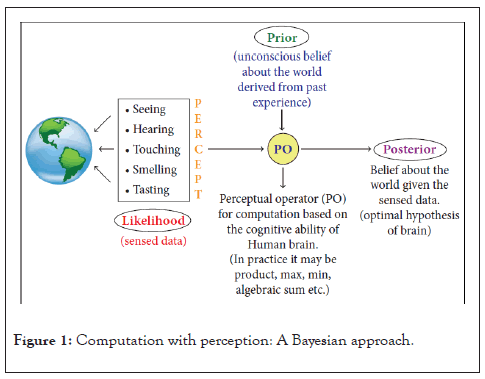
Figure 1: Computation with perception: A Bayesian approach.
Note that human brain does not execute any task using probability; But we try to mimic human computation with perception (outside the human brain) using Bayesian approach as depicted in Figure 1.
Computation with perception does not essentially deal with any specific numbers (numerical value). It is based on the resulting belief about the world obtained from the sensed data (percept) [7]. Hence in the design study we recognize an object based on the resulting belief about world of object represented by percept.
Statement of the problem
We compute the posterior probability of the world of 3D object based on the sensed data using equation (3).
We consider the 3D picture of a Kangaroo as shown in Figure 2.
Figure 2: Picture of kangaroo.
Different aspects of the Kangaroo are generated by taking projection of the object at regular interval (Figure 3). Kangaroo is placed inside the unit sphere.
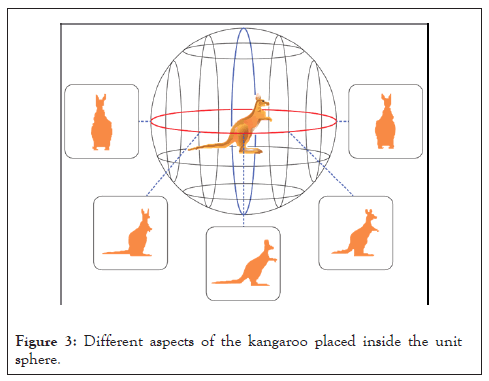
Figure 3: Different aspects of the kangaroo placed inside the unit sphere.
In (Figure 4) kangaroo is shown on the left. On the right we show a range of views from the ground plane in five degree increment. Circled view represents prototypical views. Aspect boundaries are vertical lines in green [8-10]. The posterior probability of 3D object, which is basically a Bayesian inference, provides the cognitive ability of recognition in terms of computation with perception.
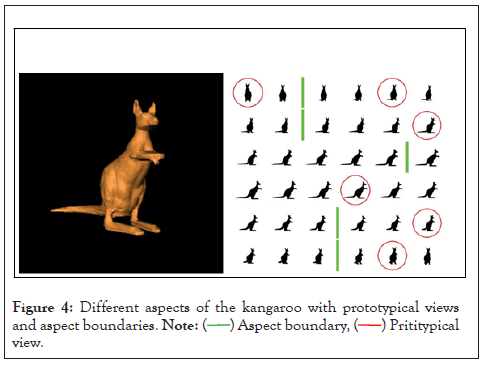
Figure 4: Different aspects of the kangaroo with prototypical views
and aspect boundaries. 
view.
Bayes rule
Let us consider the Bayes rule,
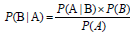…………(1)
Where, P(B │A) is Probability of B given that A occurred, P(A) is the probability of A and P(B) is the probability of B
The simplified form of Bayes rule is as follows,
P(B / A)∞P(A / B)×P(B) …………(2)
P(World / Sensed data)∞(Sensed data /World)×P(world)……….(3)
Where, World│Sensed data is Posterior (resulting beliefs about the world), Sensed data│World is Likelihood (world states generated by the sensed data), P(World) is Prior (belief about the world based on experience)
According to Helmholtz, “Perception is our best hypothesis (Guess) as to what is in the world, given our current sensory evidence and our prior experience” [5].
As per Bayes rule, the prior distribution is fixed before any data are observed.
Statistical analysis using Empirical Bayes: In contrast to Bayesian method, Empirical Bayes produces statistical inference in which the prior probability distribution is estimated from the data.
Despite this difference in perspective, empirical Bayes may be viewed as an approximation of Bayesian approach as stated above.
Derivation using approximate Bayesian
In approximate Bayesian which is basically empirical Bayesian we consider uncertainty of the parameter given the data.
Representation of likelihood function: Considering binomial distribution we get probability of likelihood as
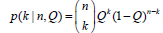…………(4)
Where k indicates the number of successful recognition of 3D object from its aspects (which are 2D images captured by a digital camera) and n indicates the total number of aspects of the 3D object.
Representation of prior probability: For representation of Prior based on approximate Bayesian (Empirical Bayesian) we are guided by a design philosophy-we can recognize an object which we have seen earlier.
Thus the prior of approximate Bayesian (empirical Bayesian) is an unconscious belief about the world which we consider for design study.
Bayesian decision theory is a normative enterprise. It represents how we reason and take decision; not how we actually execute them.
Perceptual prior decides between rival hypotheses those are compatible with current proximal input. It matches the statistics of the world we consider for design study.
Perceptual prior is mutable. Mutability of prior is necessary for perception. If the prior is not properly tuned to the environment perception will be inaccurate. We may achieve perceptual illusion if low probability is assigned to prior.
Hence for present design study, we estimate initial prior probability using Beta distribution which provides some unconscious belief or vague knowledge obtained from past experience about the world. Once we achieve posterior probability as a product of likelihood and the prior as stated above we can update the initial prior by the posterior probability which is based on initial prior. Thus the prior is updated by process of mutation and becomes more informative about the world we handle.
Computing posterior probability: Can be done by Considering Bayes rule we compute the posterior probability p(Q│n, k).
We represent Posterior as follows,
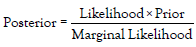…………(5)
Using equation (4) and (5) we get as follows,
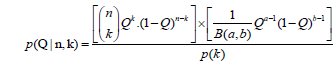…………(6)
Where, P(k) is constant because number of success full recognition of aspect is known. Thus we arrive at equation (7) which is same as equation (2).
Posterior α Likelihood × Prior …………(7)
Using equation (4) we calculate the probability of likelihood data using aspects of the object as shown in Figure 4.
We have collected total five hundred aspects of the 3D object of Kangaroo. We consider a batch of hundred aspects each time and calculate the probability of likelihood data. We consider each probability distribution of likelihood data as shown in each frame of Figure 5. Next we compute the posterior probability as a product between each likelihood and prior (see equation (7)). Thus we obtain total five posterior probability distributions. For simplicity of demonstration we map prior, likelihood and posterior on the same frame as shown in Figure 5. In Figure 5 we have shown only three frames out of five, i.e. the first frame, third frame and fifth frame. In the first frame we consider beta (4,4) for prior and derive the posterior as beta (84,24). We use the posterior as our prior for next experiment. In the fifth frame the posterior is Beta (144,64). All the five posterior probability distributions have mean value which is closely clustered around 0.75 and thus the posterior probability is stable and no further iteration is necessary.
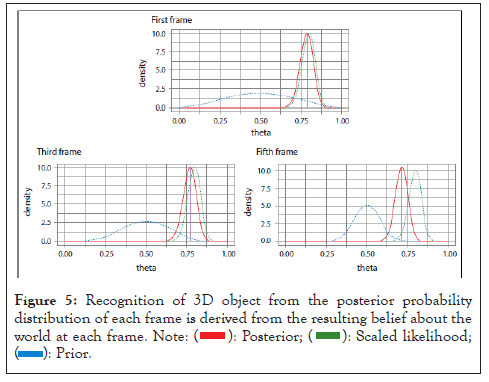
Figure 5: Recognition of 3D object from the posterior probability
distribution of each frame is derived from the resulting belief about the
world at each frame. Note: 
From five posterior probability distributions we obtain five inferences. Each inference provides information that the object is kangaroo. Thus we confirm recognition about 3D object (kangaroo) as shown in Figure 4.
Each inference derived from posterior probability is basically a hypothesis which is a belief about the world (see equation (3)). In this experiment recognition of 3D object is derived from the belief about the world as stated by the posterior probability of equation (3). Thus the five hypotheses correctly recognize the object. In case we get less number of hypothesis for correct recognition we should consider at least 80% of the total number of hypothesis of the experiment. For instance, in the present design study out of five posterior probability if four of them provide satisfactory hypothesis then computation with perception for recognition 3D object is acceptable. If it is less than four hypotheses then we should reformulate the design study.
We have successfully implemented computation with perception-a Bayesian approach. Instead of using Bayesian rule directly we consider empirical Bayes so that prior probability can be measured from the initial stage. In Bayes rule the product operation between likelihood and prior can be replaced by other operators like maximum, minimum, algebraic sum. Human combines visual and haptic information in statistical manner. In this design study we consider view likelihood and stability to recognize 3D object. We adopt these two measures to enhance the recognition process and to choose the most likely solution among all feasible views. We demonstrate the application of the above said measures by recognizing the 3D object (Kangaroo). The present study is not limited to recognize an isolated 3D object; but in general it is applicable to any complex natural 3D object.
View likelihood induces probability on the projected 2D images, which are the aspects of 3D object, by the process of projection. Thus given a prior distribution of camera orientation, which is a particular viewing direction of the camera, different probabilities are generated on the projected 2D views which are the aspects of the 3D object. It means, even if all the different camera orientations are equally likely, the images are not so. The induced probability depends on the structure of the 3D object and is always non-uniform in nature. Recent success of Bayesian approach in the field of computer vision leads to an emerging interest to apply Bayesian methods to model human visual perception. To consider the probability density function in high-dimensional space is still very complex to incorporate in Bayesian algorithm for computer vision, but development of graphical model and particle filtering techniques show some promise for implementation of efficient Bayesian algorithm. However the estimation of Bayesian algorithm in high-dimension is a challenging domain for computational neuroscientists.
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
Citation: Ray KS (2023) Bayesian Brain: Computation with Perception to Recognize 3D Objects. Int J Sch Cogn Psycho. 10:277.
Received: 02-Jan-2023, Manuscript No. IJSCP-22-20434 ; Editor assigned: 04-Jan-2023, Pre QC No. IJSCP-22-20434 (PQ); Reviewed: 18-Jan-2023, QC No. IJSCP-22-20434 ; Revised: 25-Jan-2023, Manuscript No. IJSCP-22-20434 (R); Published: 01-Feb-2023 , DOI: 10.35248/2469-9837.23.10.277
Copyright: © 2023 Ray KS. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.