Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2010) Volume 3, Issue 12
Motivation: Interpreting and quantifying labeled mass-spectrometry data is complex and requires automated algorithms, particularly for large scale proteomic profiling. Here, we propose the use of bi-linear regression to quantify relative abundance across the elution profile in a unified model. The bi-linear regression model takes advantage of the fact that while peptides differ in overall abundance across the elution profile multiplicatively, the relative abundance between the mixed samples remains constant across the elution profile. We describe how to apply bi-linear regression models to 18O stable-isotope labeled data, which allows for the direct comparison of two samples simultaneously. Interpretation of model parameters is also discussed. The incorporation rate of the labeling isotope is estimated as part of the modeling process and can be used as a measure of data quality. Application is demonstrated in a controlled experiment as well as in a complex mixture. Results: Bi-linear regression models allow for more precise and accurate estimates of abundance, in comparison to methods that treat each spectrum independently, by taking into account the abundance of the molecule throughout the entire elution profile, with precision increased by one-to-two orders of magnitude. Availability: http://mayoresearch.mayo.edu/mayo/research/biostat/splusfunctions.cfm.
Keywords: Mass spectrometry; Proteomics; Stable isotope labeling; Quantification
ALS: Alternating Least Squares; FDR: False Discovery Rate; LC: Liquid Chromatography; MS: Mass Spectrometry; MS/MS: Tandem Mass Spectrometry; SCX: Strong Cation Exchange
Characterization of the proteome is a resource of tremendous potential to understand biological processes. It is widely recognized that the DNA genetic code is insufficient to describe the proteome. Control at the level of transcription, translation, epigenetic control and post-translational processing of proteins contains key information that is beyond the genome but is necessary to unravel important mechanistic information of health and disease. Protein mass spectrometry is an attractive technology for this crucial task. The objective of quantitative proteomics via mass spectrometry is to detect and quantify all proteins that are present in a biological sample. Proteins that exhibit an increase or a decrease in abundance between two or more groups of interest (e.g., between diseased and non-diseased) are considered candidate biomarkers. Although much work is ongoing to improve the range and capacity of mass spectrometry technologies, there has been less attention to the equally important issue of optimal use and inference from the data obtained. In response, the focus herein is on developing improved analytical methods for quantifying stable-isotope labeled data.
Various labeling techniques that allow two or more samples to be analyzed simultaneously are available; we focus on 18O stable isotope labeling. 18O stable-isotope labeling is a technique used in mass spectrometry that allows for the direct comparison of two samples (Yao et al., 2001). Here, two samples undergo enzymatic digestion, one of the samples in the presence of natural H2 16O and the other in the presence of enriched H218O. For example, protein digestion with trypsin (which cleaves preferentially at lysine or arginine) in the presence of highly-enriched H218O results in the substitution of the two C-terminal carboxyl 16O atoms with two 18O atoms at high probability. As a result, peptides from the 16O- and 18O-labeled samples are mixed together and are differentiated in a mass spectrum by a four Dalton mass shift. Figure 1a provides an example of an observed joint isotopic cluster of 16O/18O-labeled peaks that were obtained from a pair of samples with an expected 1:1 ratio using 90% enriched H218O. Figure 1b illustrates that the 16O/18O joint isotopic cluster shown in Figure 1a can be theoretically separated into three overlapping sets of isotopic clusters. As descriptively displayed in Figure 1b, a 16O/18O joint isotopic cluster is comprised of a compilation of three overlapping sets of isotopic clusters: an isotopic cluster corresponding to zero 18O incorporations (cluster denoted as 16O in Figure 1b), an isotopic cluster shifted to the right by two Daltons that corresponds to the incorporation of a single 18O into one of the two possible carboxyl oxygens (cluster denoted as 18O1) and an isotopic cluster shifted to the right by four Daltons that correspond to two 18O incorporations (cluster denoted as 18O2). Each of the overlapping isotopic clusters consists of a monoisotopic peak (defined as the peak that contains the most abundant isotope for each element: 12C, 1H, 14N, 16O, 32S, etc.) along with secondary peaks shifted by 1, 2, 3, etc. Daltons that correspond mainly to 13C isotopes.
Figure 1: (A) An example of an observed joint isotopic cluster of 16O/18Olabeled peaks using 90% enriched H2 18O that was detected in a single elution time spectrum from a pair of samples with an expected 1:1 ratio. (B) An illustration of how the 16O/18O joint isotopic cluster shown in (A) is comprised of three overlapping sets of isotopic clusters. (C) The full elution profile for the molecular species displayed in (A).
Because 18O-labeled data is a compilation of three overlapping sets of isotopic clusters, quantification of 18O-labeled data must carefully consider three important concepts. First, the quantification method must be able to recognize and separate the three sets of overlapping clusters. As displayed in Figures 1a-b, cluster 18O1 contains isotopes from cluster 16O and likewise, cluster 18O2 contains isotopes from clusters 16O and 18O1. Second, the 16O isotopic cluster is a combination of the unlabeled (16O-labeled) peptides and the contributions from the 18O-labeled sample that failed to incorporate and 18O at both carboxyl oxygens. For example, the C-terminal peptides for each protein will remain unchanged in the labeled samples. Thus, in order to accurately determine the amount contributed by each of the labeled and unlabeled samples, the quantification method must be able to separate these two sets of species. Lastly, the percent of 18O-incorporation is peptide specific and thus necessitates estimation during the quantification process. These artifacts of 18O labeling make quantification by eye very difficult and thus require automated algorithms.
Extending the methods of Mirgorodskaya et al. (2000) and Johnson and Muddiman (2004), Eckel-Passow et al. (2006) developed a multivariable regression model that quantifies 18O-labeled data. Particularly, the multivariable regression model uses the average amino acid averagine - which only requires a peptide's molecular mass - to approximate the chemical composition (distribution of naturally occurring isotopes). Thus, there is no need to run a labeled sample independently in order to derive the chemical composition or to carry out tandem MS to obtain identification information before performing quantification. Furthermore, the multivariable regression model directly estimates the peptide's incorporation rate of the 18O label, resulting in estimated abundances that are adjusted for the corresponding incorporation rate. This is in direct comparison to algorithms that require a reverse labeling design - and therefore, twice as many resources - in order to estimate the incorporation rate (Andersen et al., 2009).
More recently, Zhu et al. (2010) proposed a Markov-chainbased heteroscedastic regression model for quantifying 18O-labeled data. The regression model by Zhu and colleagues is similar to the multivariable regression model proposed by Mirgorodskaya et al. (2000) and Eckel-Passow et al. (2006); however, the heteroscedastic regression model accounts for technical and biological variability. The heteroscedastic regression model was motivated by MALDI-TOF/ TOF data, where technical replicates are commonly employed (i.e., mixtures are often spotted multiple times on a MALDI plate) and thus it is of interest to capture the variability due to technical replicates while performing quantification. Conversely, our data are fractionated by liquid chromatography (LC) and subsequently analyzed by a LTQOrbitrap mass spectrometer. As such, we propose a quantification method that takes into account the chromatographic fractionation process during quantification of 18O-labeled data.
Because putative biomarkers are believed to exist at low levels of abundance (Anderson and Anderson, 2002) and current mass spectrometry technologies have limited dynamic range capabilities, samples are often fractionated in order to more fully characterize the proteome. As an illustration, the elution profile for the joint isotopic distribution displayed in Figure 1a is provided in Figure 1c. The elution profile of a molecule is generally bell shaped; it initially elutes at low abundance, hits a maximum and then trails off. When using reverse phase LC, a peptide might be present in few or many adjacent elution-time spectra depending primarily on the abundance and amino acid sequence of the peptide.
Most quantification methods are step-wise procedures that treat each MS spectra independently and thus perform quantification within each MS spectra. Subsequently, for each peptide, the relative abundances are integrated over all spectra containing the peptide (e.g., Andersen et al., 2009; Ramos-Fernández et al., 2007; Eckel- Passow et al., 2006; Hicks et al., 2005; Johnson and Muddiman, 2004; Mirgorodskaya et al., 2000). With respect to fractionation, the peptides will differ across LC fractions in overall abundance; however, the relative abundance between the mixed samples remains the same across the fractions and will result in the same relative abundance. Hence, isotopic clusters that denote the same peptide will share the same model parameters relating to relative abundance. Here, we illustrate the use of bi-linear models for quantifying 18O-labeled data, which affords the ability to model across the fractionation variable in a unified model. A unified model allows for more accurate estimates of abundance for each peptide particularly at the beginning and end of the elution profile, where the abundances are low.
Data
1:1 Data: Human transferrin and bovine serum albumin were trypsin digested together in either 90% 18O water or 100% 16O water and subsequently mixed 1:1. The mixed sample was fractionated using liquid chromatography and subsequently analyzed by a LTQOrbitrap mass spectrometer (ThermoFisher). Because both proteins were present in equal concentrations in both the 18O-labeled and unlabeled (16O) samples, the expected relative abundance for both proteins is 0.50 (relative abundance = 16o/(16o+18o). Nano-scale LC separations were performed on a 15 cm long by 75 micron inner diameter spray tip packed with Magic C18AQ, (5 um, 200 Å, Michrom BioResources) using a gradient from 5% to 40% acetonitrile in 0.2% formic acid over 60 minutes at a flow rate of 0.4 uL/min. (Eksigent NanoLC-1D). An autosampler was used to load 10uL of 50 ng/uL sample onto a 0.25uL OptiPak (Optimize Technologies) trap packed with Michrom Magic C8, 200Å stationary phase. Orbitrap survey scans (60,000 resolving power at m/z 400, AGC target 1 × 106 charges) were used to select the top six precursor ions between m/z 350 and 1950 for data-dependent acquisition of tandem mass spectra in the linear ion trap. Peptides eluted between 10 and 60 minutes.
Complex mixture
Plasma was obtained from patients before and after administration of branched chain amino acids, a dietary supplement believed to stimulate protein production. Plasma samples were depleted of abundant proteins using an Agilent MARS-14 affinity column, trypsin digested, enzymatically labeled using H2 16O and 90% enriched H2 18O, 16O and 18O samples combined and fractionated by strong cation exchange (SCX) chromatography on a polysulfoethyl aspartamide column using a KCl gradient in phosphate buffered mobile phases. Herein, we show the results from the first SCX fraction associated with one pair as a representative sample. LC-MS/MS acquisition parameters for these samples were as described above with the following changes: an 18 cm long column was used in conjunction with a 50 minute gradient from 5% to 50% acetonitrile. Peptides eluted between 10 and 50 minutes. MS/MS precursors were selected from the top 5 doubly- and triply-charged precursors between m/z 375 and 1600.
Peptide/protein identification
The tandem mass spectra acquired in parallel with the Orbitrap survey spectra used for quantification, were used to assign peptide sequence. Tandem mass spectra (MS/MS) were searched against the human subset of the SwissProt protein database appended with decoy entries consisting of the reversed sequences for each protein entry in order to set determinant score thresholds for a 1% false discovery rate (FDR). Searches were performed with 20 ppm precursor mass tolerance, 0.6 Dalton fragment tolerance, carbamidomethyl-cysteine as a fixed modificiation and allowing for variable modifications of oxidized methionine and 18O2 on the carboxy terminus. The SWIFT workflow tool, developed in-house, prepared input search files for each MS/MS spectrum (Xtractmsn) submitted spectra to Mascot (Matrix Science), Sequest (Thermo Fisher Scientific) and X!Tandem (Global Proteome Machine) search engines and combined and submitted search results to Scaffold 2 (Proteome Software) to determine statistically significant identifications. Valid peptide sequence identifications at the 1% FDR level were matched to 16O/18O quantification results by precursor m/z and LC retention time.
Statistical methodology
Eckel-Passow et al., (2006) developed a linear regression model for 18O stable-isotope labeled mass-spectrometry data that quantifies the amount present in each of the two represented samples for each joint isotopic cluster. The joint isotopic distribution is estimated using a multivariable linear regression model, which is an extension to the work of Johnson and Muddiman (2004) and Mirgorodskaya et al. (2000). Let y0 , y1,..., yn-1 be a vector of n peak heights at a spacing of one Dalton that represent a joint isotopic cluster (peptide) as determined from some peak-detection procedure. Also, assume y0 corresponds to the monoisotopic peak from the unlabeled sample. Eckel-Passow et al. (2006) showed that
E(y) = (XD)β. (1)
X is a fixed design matrix containing the expected isotopic distribution for the corresponding peptide,
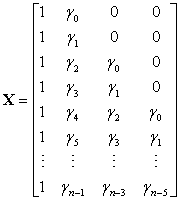
and γ0 , γ1 ,... denotes the expected abundance distribution, where γi is the abundance of the peptide that has i extra neutrons due to natural isotopes. Eckel-Passow and colleagues used averagine (Senko et al., 1995) to estimate the expected isotopic distribution, which does not require that the amino acid sequence be known. More recently, Valkenborg et al. (2008) proposed the use of relative ratios for estimating isotopic distributions, which more accurately estimates the sulfur content. D is a known matrix based on the purity of the 18O water,
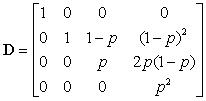
and p denotes the purity of the 18O water. For the data presented herein, p = 0.90. Lastly, β is a 3 × 1 vector of estimable parameters, which is constrained to be non-negative. The estimated regression parameters 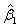 ,
, 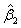 and
and 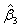 denote the amount of the molecule in the mixed sample that had an exchange in 0, 1 and 2 18O atoms at the C-terminals, respectively. The parameters (
denote the amount of the molecule in the mixed sample that had an exchange in 0, 1 and 2 18O atoms at the C-terminals, respectively. The parameters (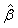 ) are not of primary interest; of primary interest are θ16 and θ18, corresponding to the relative abundance of the peptide originating from the 16O (also referred to as the "unlabeled sample") and 18O-labeled samples. The expected values of β1, β2 and β3 are E(β1) = θ16 +(1-p)2θ18, E(β2) = 2p(1-p)2θ18 and E(β3) = p2θ18, respectively, where p denotes the known proportion of 18O water in the 18O-enriched water. The values of interest (θ16 and θ18, which denote the relative abundance of the corresponding molecule in the 16O- and 18O-labeled samples) are thus simple functions of the parameter estimates. Eckel-Passow and colleagues also show that the incorporation rate can be estimated by
) are not of primary interest; of primary interest are θ16 and θ18, corresponding to the relative abundance of the peptide originating from the 16O (also referred to as the "unlabeled sample") and 18O-labeled samples. The expected values of β1, β2 and β3 are E(β1) = θ16 +(1-p)2θ18, E(β2) = 2p(1-p)2θ18 and E(β3) = p2θ18, respectively, where p denotes the known proportion of 18O water in the 18O-enriched water. The values of interest (θ16 and θ18, which denote the relative abundance of the corresponding molecule in the 16O- and 18O-labeled samples) are thus simple functions of the parameter estimates. Eckel-Passow and colleagues also show that the incorporation rate can be estimated by
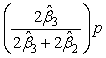 , where p denotes the known purity of the 18O water.
, where p denotes the known purity of the 18O water.
Here, we propose that improved quantification is achieved by modeling across the fractionation device in a unified model using bilinear regression. The overall abundance of the isotopic clusters varies in a multiplicative, rather than additive, fashion across the elution profile. Data that is collected serially, such as mass-spectrometry data, can be modeled using multi-linear regression where the expectation of the data matrix can be written as the product of parameters (Bro 1997; Linder and Sundberg, 1998; Leurgans and Ross 1992). When only two experimental variables are considered, multi-linear models are referred to as bi-linear models. Multi-linear models have been used for more than a decade for quantification in chemometrics (Linder and Sundberg 1998; Leurgans and Ross 1992; Fraga and Corley 2005); Leurgans and Ross (1992) provide an overview of multilinear regression models.
A bi-linear regression model affords the flexibility to incorporate variables that allow quantification across the fractionation device in a unified approach and therefore, allows the use of a large number of data points for quantification resulting in more precise measurements of relative abundance. The input data for the bi-linear regression model consists of a peak list that encompasses a single peptide, consisting of mass, abundance, charge state and fraction (e.g., chromatographic elution time). The creation of this list requires the use of other software (e.g., Cox and Mann, 2008; Mason et al., 2006).
To model multiple joint isotopic distributions that denote the same peptide present in a given sample, the model proposed by Eckel-Passow et al. (2006) is extended to
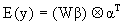 (2)
(2)
where y = [y1,., yh] is a n × h matrix where each column denotes an isotopic cluster with n peak heights. We allow only a single missing peak height in each column and replace the missing value with a zero. By doing so, we are assuming that any observed isotopic clusters that have more than one missing peak are clusters that were falsely identified by the corresponding peak-picking procedure and thus we do not attempt to quantify them. W = (XD), where X is a design matrix based on the expected isotopic distribution, D is a matrix based on the purity of the 18O water, β is a 3 × 1 vector of estimable parameters, α is a h × 1 vector of estimable parameters and 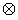 denotes the Kronecker product. The model is linear in β conditional on α and linear in α conditional on β; with two multiplicative parameters this is called a bi-linear regression model. The bi-linear model estimates a common β (a common set of abundances that denote the amount of the molecule in the mixed sample that had an exchange in 0, 1 and 2 18O atoms at the C-terminals, respectively) across isotopic clusters that denote the same peptide while allowing for an overall abundance shift (α) between isotopic clusters.
denotes the Kronecker product. The model is linear in β conditional on α and linear in α conditional on β; with two multiplicative parameters this is called a bi-linear regression model. The bi-linear model estimates a common β (a common set of abundances that denote the amount of the molecule in the mixed sample that had an exchange in 0, 1 and 2 18O atoms at the C-terminals, respectively) across isotopic clusters that denote the same peptide while allowing for an overall abundance shift (α) between isotopic clusters.
Much attention has been given to fitting algorithms for bi-linear models in the literature; Faber et al. (2003) provide an extensive review. Alternating least squares (ALS) is the most flexible algorithm and Faber and colleagues show that while it is slower than other approaches, it produces generally superior results. Constrained ALS is utilized here, constraining the elements of β to be non-negative in order to be biologically plausible. Additionally, we apply the constraint that 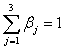 ,which implies that the summed relative abundance for the corresponding molecule across the two samples equals one (θ16 + θ18 = 1).
,which implies that the summed relative abundance for the corresponding molecule across the two samples equals one (θ16 + θ18 = 1).
For the 1:1 human transferrin and bovine serum albumin data, Averagine was used to estimate the expected isotopic distribution and an in-house extension to MaxQuant (Cox and Mann 2008) was used to derive the peak lists. We detected 280 species, which mapped to 134 peptides and 15 proteins. The peptide masses ranged from 734 to 4987 Daltons. We observed a minimum of 6 and a maximum of 416 peaks per species (44 and 99 are the 25th and 75th percentiles, respectively) and a minimum of 1 and a maximum of 36 joint isotopic clusters per species (6 and 12 are the 25th and 75th percentiles, respectively). This implies that there were species that were observed in a single retention-time spectrum as well as species that were observed in as many as 36 retention-time spectra.
As proof of principle, we fit the bi-linear regression model to the 1:1 data. Table 1 compares the results of using the single cluster regression model described by Eckel-Passow et al. 2006 and the proposed bi-linear model for the specie displayed in Figure 1, which was detected across eleven spectra as it eluted from the LC column. We would expect to obtain a relative abundance of 0.50 since the two samples were mixed 1:1; the bi-linear model obtained a ratio of 0.519, whereas the single-cluster model had ratios that ranged from 0 to 0.548 across the eleven elution-profile clusters. For the single-cluster model, the clusters are numbered according to when they eluted from the LC column in Table 1; cluster 1 eluted first and cluster 11 eluted last. Strikingly, the variances associated with the single-cluster models are one-to-two orders in magnitude larger in comparison to the variance obtained using the bi-linear model. Moreover, at the beginning and end of the elution profile (when the absolute abundance is at or below the noise threshold) the single-cluster model has difficulties estimating relative abundance.
| Model | Cluster | θ16 | Variance | Incorporation Rate | Number Non-zero Peaks |
|---|---|---|---|---|---|
| Bi-Linear | Overall | 0.519 | 0.0084 | 0.887 | 75 |
| Single-Cluster | 1 | 0.538 | 0.064 | 0.900 | 7 |
| 2 | 0.527 | 0.037 | 0.878 | 8 | |
| 3 | 0.515 | 0.031 | 0.875 | 8 | |
| 4 | 0.517 | 0.035 | 0.874 | 8 | |
| 5 | 0.517 | 0.040 | 0.881 | 8 | |
| 6 | 0.548 | 0.048 | 0.899 | 8 | |
| 7 | 0.528 | 0.068 | 0.900 | 7 | |
| 8 | 0.507 | 0.258 | 0.900 | 6 | |
| 9 | 0 | NA | 0.900 | 5 | |
| 10 | 0 | NA | 0.900 | 5 | |
| 11 | 0 | NA | 0.900 | 5 |
Table 1: Comparison of the performance of the bi-linear model and the singlecluster regression model for a single molecular species that was detected across 11 elution spectra. Clusters are numbered in the order in which they eluted from the LC column. The single-cluster model is that described in Eckel-Passow et al. (2006).
Thus, as discussed in White et al. (2009), quantification precision is enhanced when species are evaluated over the retention-time profile. Additionally, Cox and Mann (2008) discuss that mass precision is improved when species are evaluated over the retention-time profile.
Figure 2 provides a stick representation of the estimated α obtained from fitting the bilinear model defined in equation 2. As expected, the estimated α follow the observed elution profile; the observed elution profile is provided in Figure 1c.
Figure 3a displays the estimated relative abundances for the peptides that matched to Bovine serum albumin, relative to their estimated incorporation rate. Similarly, Figure 3b displays the estimated relative abundances for peptides that matched to Human transferrin, relative to their estimated incorporation rate. A density curve is included in both figures; a density curve is a smooth curve fit on the distribution of relative abundance values that represents the proportion of species that have the corresponding relative abundance. The peptides associated with both proteins are expected to have a relative abundance of 0.50. As displayed by the density curves, the estimated relative abundances are slightly biased upward for both proteins. Additionally, although most peptides have relatively high incorporation rates, there are peptides that either do not incorporate the 18O label at all (incorporation rate equals zero) or poorly incorporates the 18O label. Ramos-Fernández et al. (2007) similarly reported a range of estimated labeling efficiencies and proposed eliminating all species with an estimated incorporation rate less than 0.40 suggesting that they are unreliable.
Figure 3: (A) The observed relative abundances (denoted Theta1) for the peptides that matched to Bovine serum albumin, relative to their estimated incorporation rate. (B) The observed relative abundances (denoted Theta1) for peptides that matched to Human transferrin, relative to their estimated incorporation rate. A vertical reference line at Theta1=0.5 and a density curve are included in both figures; a density curve is a smooth curve fit on the distribution of relative abundance values that represents the proportion of species that have the corresponding relative abundance.
We also applied the proposed bi-linear model to data from a complex mixture. For the branched chain amino acids data, Averagine was used to estimate the expected isotopic distribution and an in house extension to MaxQuant (Cox and Mann 2008) was used to derive the peak lists. Evaluating a single SCX fraction, we detected 298 species, which mapped to 173 peptides and 37 proteins. The peptide masses ranged from 765 to 4255 Daltons. We observed a minimum of 8 and a maximum of 380 peaks per species (47 and 129 are the 25th and 75th percentiles, respectively) and a minimum of 2 and a maximum of 44 joint isotopic clusters per species (8 and 17 are the 25th and 75th percentiles, respectively). This implies that there were species that were observed in a single retention-time spectrum as well as species that were observed in as many as 44 retention-time spectra.
Figure 4 displays the estimated relative abundances for the 173 identified peptides in the branched chain amino acids data, relative to their estimated incorporation rates. Because we do not expect most proteins to be differentially regulated before and after administration of branched chain amino acids, we expect most peptides to have a relative abundance equal to approximately 0.50. Peptides for which the relative abundance is less than or greater than 0.50 are peptides that are potentially stimulated by the diet supplement. As was also observed in the 1:1 data displayed in Figure 4, most peptides have relatively high incorporation rates, however, there are peptides that either do not incorporate the 18O label at all or poorly incorporate the 18O label. Based on Figure 4, it appears that it might be reasonable to conclude that any peptide with an observed incorporation rate <0.40 was unreliably measured, similar to the recommendations of Ramos-Fernández et al. (2007). Using this rule for the branched chain amino acids data would result in the removal of 52 peptides.
Figure 4: The observed relative abundances (denoted Theta1) for the 173 identified peptides in the branched chain amino acids data, relative to their estimated incorporation rates. A vertical reference line at Theta1=0.5 and a density curve are included; a density curve is a smooth curve fit on the distribution of relative abundance values that represents the proportion of species that have the corresponding relative abundance.
The ability to label samples and subsequently combine them for simultaneous mass analysis reduces run-to-run variation as well as overall instrument time. However, interpreting the resulting spectra and obtaining estimates of relative abundance poses greater complexity in this situation. We showed that bi-linear regression is appropriate for quantifying 18O-labeled mass-spectrometry data. Furthermore, by modeling the isotopic cluster over the elution profile in a unified model, the bi-linear model provides more accurate and precise estimates of relative abundance over methodologies that treat each spectrum independently.
Here, we showed how bi-linear regression can be used to model relative abundance across the elution profile of a molecular species. However, the proposed bi-linear methods could be extended to also model across charge state, SCX fraction, or other factors thought to contribute to overall abundance shifts using multi-linear regression. For example, peptides generally exist at multiple charge states within a spectrum due to the nature of the ionization process, particularly for electrospray ionization. A peptide will differ in overall abundance across charge states; however, the relative abundance between the mixed samples will remain the same across charge states. Similarly, a peptide will differ in overall abundance across SCX fractions; however, the relative abundance between the mixed samples will remain the same across SCX fractions. The model performance together with parameter stability will need to be evaluated as the number of experimental variables increases. To our knowledge, closed form standard errors are worked out for bi-linear models but not for multilinear models with three or more experimental variables. Additionally, although we used averagine to estimate the isotopic distributions (i.e., to estimate the expected abundance distribution in equation 1), the proposed bilinear model does not require that averagine be used. The expected abundance distribution can be defined using any method to estimate the isotopic distribution (e.g., Valkenborg et al., 2008); however, few methods exist that do not require information about peptide sequence.
Recently, Zhu et al. (2010) proposed a Markov-chain-based regression model for quantifying 18O-labeled data that has the ability to estimate the inter-replicate and inter-biological variability. Their methods were motivated by MALDI-TOF/TOF data where technical replicates are readily available from which to estimate variability due to technical replicates. Our samples are fractionated by LC and subsequently mass analyzed by a LTQ-Orbitrap and we do not have technical replicates. However, instead of estimating inter-replicate variability, one may be interested in estimating the inter-spectra variability resulting from LC fractionation. Zhu and colleagues have not made their code readily available and so we were unable to compare our methodologies with theirs. Additionally, Zhu and colleagues discussed the implementation of their algorithm on a controlled experiment and not on a mixture of complex samples and thus the utility has not been fully evaluated.
Additionally, the approach described by Zhu et al. (2010) accounts for 17O-atoms in addition to 16O- and 18O-atoms, whereas the approach described herein does not. However, we estimate the effect due to 17O-atoms in these data is minimal. The 18O water used in these experiments was from a lot of minimum of 99% atom percent enriched in 18O and packaged in 1 gram ampoules (Isotec). A subsequent assay of one of our ampoules by the vendor three years after purchase determined the composition to be 98.2% 18O, 2.2% 16O and < 0.1 % 17O. The natural isotopic composition of oxygen atoms is 99.759% 16O, 0.204% 18O and 0.037% 17O and any change over time to the composition of the 18O-enriched water would be toward the naturally occurring composition. Additionally, since we are interested in the 18O1 and 18O2 species, the contribution of 17O is of very little consequence at those masses.
Quantification of 18O-labeled data is typically performed at the full-scan (MS) level, as we have proposed. However, White et al. (2009) recently proposed a method for quantifying 18O-labeled data at the tandem (MS/MS) level. Choosing the most appropriate methodology depends on the research objective. If one is only interested in finding candidate biomarkers that can be successfully identified via current peptide/protein databases, then methodologies that are applicable to either MS or MS/MS data are relevant. However, if one would like to mine all of the available data, or at least have it available to mine in the future, then methodologies that quantify at the MS level would be preferred. We tend to favor the later route, as others have (Cox and Mann 2008). That is, as a first pass, we typically only statistically analyze the identified species and evaluate their association with outcome. However, we have all the data available in case we want to also analyze the currently un-identified species to potentially identify novel features.
To our knowledge, only the methodologies of Zhu et al. (2010) and the bi-linear model discussed herein utilize information across multiple spectra in a unified model to obtain estimates of relative abundance for 18O-labeled data. The methodologies proposed by Zhu et al. (2010) were motivated by MALDI data where technical replicates are available and thus their models estimate the inter replicate and inter-biological variability. The proposed bi-linear models were motivated by serially-collected data, particularly, data that were fractionated via LC and subsequently analyzed by a LTQOrbitrap mass spectrometer. The bi-linear model, which assumes a common relative abundance across the elution profile, allows for more accurate and precise estimates of relative abundance across the entire elution profile. Further- more White et al. (2009) and Cox and Mann (2008) discuss the benefits in terms of more accurate quantification and improved mass accuracy when species are evaluated over the retention-time profile.
This work was supported by the National Institutes of Health [R33 DK70179]; the Mayo Clinic CTSA [UL1 RR024150] from the National Center for Research Resources; Fraternal Order of Eagles Cancer Fund; David Woods Kemper Memorial Foundation; and a generous gift from Gordon and Elizabeth Gilroy.