The fundamental role and effects of enzymes in the key processes of DNA replication and transcription have been deeply addressed during the last ten years. In fact, it is well established nowadays that the initiation of DNA transcription is tributary to the synthesis of the polymerase-RNA which is known as the main factor contributing to break the strong hydrogen bonds linking bases in pairs, for the genetic code to be exposed out of the stack. Unlocking the complexity of such a phenomenon has then been shown to mainly depend on the DNA complex structure, as it requires, among the numerous involved degrees of freedom, the unwinding of the double helix. That complexity mainly comes from its structure which is primarily made of random distributions of four types of bases, adenine (A), thymine (T), cytosine (C) and Guanine (G). Besides, the pairing of the bases respects a universal complementarity where A can bind only to T and C to G. The bases are put together by hydrogen bonds, and the AT pair contains two H-bonds while the GC pair contains three of them. Among the models introduced to describe the dynamics of such a complex molecule, the Peyrard-Bishop (PB) model [1,2] has been extensively used in the last ten years because of its capability of predicting the occurrence of denaturation bubbles as widely observed in experiments where the so-called first-order phase transition emerges [2,3]. Furthermore, many studies have been carried out, showing that it support solitonic structures and is rather suitable to observe the localization of the energy which drives the key dynamical processes known as replication and transcription. Over the years, the PB model has been improved to take into account other features such the helicoidal structure of DNA [4,5], the cooperativity among adjacent base pairs [6,7] and the roto-torsional behaviours of the molecule [8-11]. For example, modifications brought to the PB model have shown new features in the way the base pairs oscillate and its modulational instability has been extensively studied as well [5]. Analytical solutions of the helicoidal PB model have been studied [12], but no relationship has been established, to our knowledge, between fluctuating bubbles and soliton emergence in DNA nonlinear models. The main objective of the present work is therefore to show that wave mixing can has some features of fluctuating bubbles and can be used to explain the opening of the DNA double helix. For this purpose, we use the so-called asymptotic expansion to derive the amplitude equations of the interacting waves. In fact, we assume that the RNA-polymerase which breaks H-bonds behaves as a wave which interacts with breathing modes so that the transcription bubble emerges. The helicoidal PB model we consider in this work is described by the Hamiltonian [4,10].

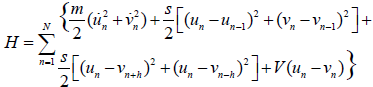(1)

While the first term of Eq. (1) represents the kinetic energy, the second one stands for the nearest-neighbour stacking energy with coupling parameter s. In the helicoidal configuration of the DNA chain, nucleotides from different strands and close enough to interact via filaments of solvent. Otherwise, the nucleotide n of one strand interacts with the nucleotides (n - h) and (n - h) of the other strand. This is given by the third term in Hamiltonian (1). Also, the helicoidal pitch of DNA being 11 per turn, we consider h=5. S is the helicoidal coupling parameter and the on-site potential is the Morse potential 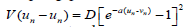, where D is the dissociation energy and a parameter homogeneous to the inverse of a length, which sets the spatial scale of the potential.

The Hamiltonian (1) gives the equations of motion for u_n and v_n. Furthermore, by using the center-of-mass coordinates representing the in-phase and the out-of-phase transversal motions, i.e.,

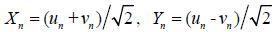(2)

it is possible to decouple the two variables un and v_n as follows

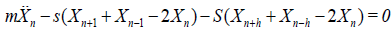(3a)

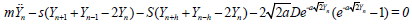(3b)

The first equation admits plane wave solutions and does not really interests us as the second one which support localized structures. We will therefore work with Eq. (3b). The rest of the paper is then organized as follows. In section 2, we first use the multiple scaling expansion to show that interacting waves can be described via a set of coupled nonlinear Schrodinger (NLS) equations and we study their modulational instability (MI). We show that the coupling mode enlarges the instability domain and therefore brings about new features in the bearing of modulated trains of waves in the helicoidal PB model. In section 3, we derive solitonic solutions for both for the single and coupled modes and we show that the coupled mode gives rise to fluctuating bubbles at their interaction point. Concluding remarks end the paper.

Amplitude equations

In order to use the multiple-scaling method, we first expand the terms in exponential up to the third order, and reduce Eq. (3b) to

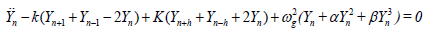(4)

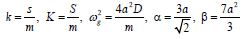
Investigating the effects of nonlinearity and discreteness through the asymptotic expansion imposes us to assume the following quasidiscreteness approximation [13-1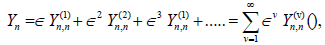5].

(5)

where ? is a small, but finite, parameter which stands for the relative amplitude of the excitations. In its general form, 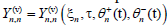where the first and second subscripts n represent the variables 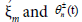respectively. Along the same line, the slow variables ξ_n = ?(nl-μt) and τ=?²t are also known as the multiple scale variables. μ is a small variable which will be determined by a solvability condition. The fast variables 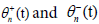represent the phases of two carrier, but counter-propagating, waves. Considering the derivative expansion

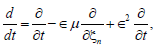(6)

and taking into account all the above hypotheses, and using the Taylor's exapansions

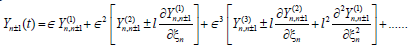
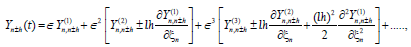(7)

the problem to solve reduces to the following set of equations

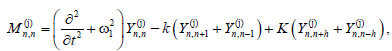(8)

With

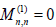
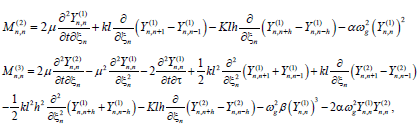(9)

Where 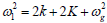Solving the above system (8) will be performed step by step. For j=1,

one can easily get the solution

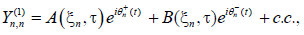(10)

Where A(ξ_n, τ) and B(ξ_n, τ) are envelope functions to be determined later, with 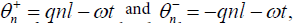with ω being the carrier wave frequency, related to the carrier wavenumber q via

the dispersion relation

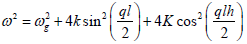(11)

For j=2, the solvability condition

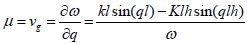(12)

is found and the terms in 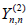is given by

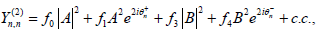(13)

Where

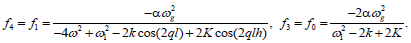
For j=3, the solvability condition leads us to the set of coupled equations for the amplitudes A and B as follows

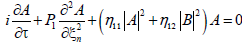(14a)

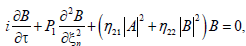(14b)

Coming back to original variables, τ=?²t and ξ_n=ε(nl-μt)=εx, imposes us to set (ψ₁, ψ₂)=ε(A,B), and the set of equations (14) becomes

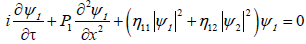(15a)

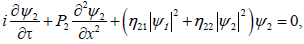(15b)

Where

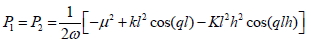
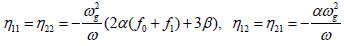(16)

The set of equation (15) describes the possibility of wave mixing in the helicoidal model of DNA. We should however stress that it is nowadays well introduced in the DNA dynamics as clearly discussed by Tabi et al. [15,16]. Besides, it also appears in a broad range of physical settings such electrical lattices [17], Bose-Einstein condensates [18], plasma physics [19], just to cite a few. In electrical transmission lines, for example, it has been shown to bring about modulated turbulent patterns [20]. In the case of the Peyrard-Bishop model, coupled NLS equations have been shown to bring about kink-breather solitonic structures with interesting biological implications for the processes of DNA breathing [15]. In the meantime, the process of wave mixing has not yet been addressed in DNA and could give rise to new features in the process of bubble emergence

Modulational instability

The most direct way solitonic structures emerge in nonlinear systems is through MI. In order to investigate the possibility of wave mixing in the set of Eq. (15), we assume that it admits the plane waves 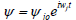as solutions, where the real constants ωj(j=1,2), and the complex amplitudes 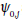are related by the equations.

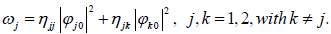(17)

In order to investigate the stability of the plane wave solutions, we perturb slightly their amplitude as 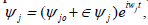where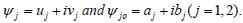 After linearizing around the unperturbed waves and separating the real from the imaginary, from the previous assumption, wet assume 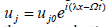+ c.c.and 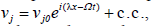where λ and Ω are the perturbation wave number and perturbation, respectively. We therefore obtain an homogeneous system for u_0j and v_0j as follows

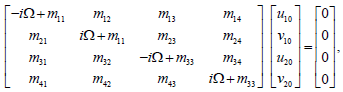(18)

Where

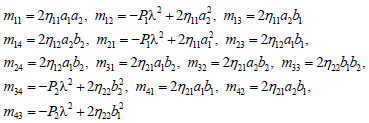(19)

The condition for the above system to have nontrivial solutions is obtained by setting its determinant to zero, which leads us to the following nonlinear dispersion relation:

Ω⁴-P Ω²+Q=0, (20)

Where

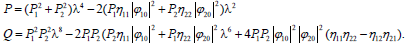(21)

Solutions for Eq. (20) can easily be found as

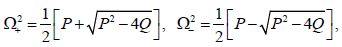(22)

therefore, for the plane wave solutions to be stable under modulation, the conditions P>0, Q>0 and Δ=P²-4Q>0 should be simultaneously fulfilled. In other words, when this is effective, the plane waves will be expected to spread in the molecule without any change. On the other hand, solutions (22) could also be complex and this may deeply depend on the sign of the discriminant Δ On this background, the instability is a purely growing mode for Δ>0 and the growth rate of instability Δ can be obtained as 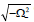This growth rate will then be positive if P<0, i.e., 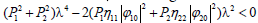leading to the condition 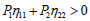for σ to remain positive, with 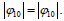Accordingly, the condition Δ>0 implies Q>0, i.e.,

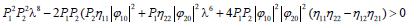
Since P₁=P₂, the plane wave solutions will be stable if 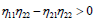and unstable if the later is not satisfied. Otherwise, for Δ<0, the growth rate of instability is given by 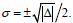σ is represented in Figure 1, both for the single and coupled modes, versus the perturbation wavenumber λ. For the single mode, the region of instability is situated in the interval 0<λ<0:35π, while for the coupled mode, unstable wave patterns are expected to take place in the region 0<λ<0:65 π. To remind, the single mode is obtained for 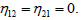Uncoupled identical NLS equations are then obtained, with the same stability/instability features. On the other hand, the coupled mode implies 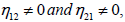and takes account of the nonlinear coupling between the two NLS equations. Comparing qualitatively these two cases, one sees that coupled modes expand the regions of instability and even cover the unstable region for the single mode. Also, the growth rate of instability is high for the coupled modes. On this basis, we also suspect the unstable modes from these two cases to be different. However, this can be verified through direct numerical simulations on the generic equation (3b). This has been done using the fourth-order Runge-Kutta computation scheme on a chain of 350 base pairs with periodic boundary conditions and time-step Δt=10-3 tu. The wavenumber have been fixed as ql=0.28 π and λ=0.15 π, values which fall well inside the instability regions of the two modes. The corresponding results are given in Figure 2, where panel (a) shows the MI features of the single mode and panel (b) displays nonlinear oscillations of the coupled mode. In both cases, trains of soliton-like structures, with breathing features, are observed. Their importance in collecting the energy necessary for the initiation of the key precesses of replication and transcription has been discussed in many DNA nonlinear models, with suitable biological implications [7,10,12]. Indeed, the breaking of the hydrogen bonds starts with slight oscillations of the bases and then grow progressively in amplitude under the action of RNA-polymerase till the breaking of the hydrogen bond, condition for the genetic information to be collected by the messenger- RNA. This suggest the presence of many modes that contribute to collect such an energy, leading to some modification of the way DNA strands breathe [21-23]. For example, the single mode here displays one-humped oscillatory structures (Figure 2a), while trains of multibreather elements correspond to the coupled mode (Figure 2b). Also, one can notice that the structures that emerge in the second case are highly localized in comparison to the single mode. It is the clear that coupled modes could bring about new features in the way hydrogen bonds oscillate an therefore need to be regarded in the cases of highly localized structures and bubbles.

Figure 1: Plot of the instability growth rate for the single (red line) and coupled (blue line) modes for m=300 amu, s=0.04 eV/Ų, D=0.15 eV, a=6.3 Å^-1 and S=0.001 eV/Ų.

Figure 2: The panels show development of MI in the (a) single (b) coupled modes. The parameters are m=300 amu, s=0.04 eV/Ų, D=0.15 eV, a=6.3 Å^-1 and S=0.006 eV/Ų.

The single mode

For the single mode, we assume 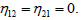and the system reduces to two identical and uncoupled NLS equations. The equation for ψ₁ is for example given by

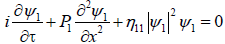(23)

and admits the solution [15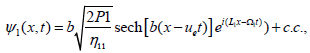,24]

(24)

which is the same for the NLS equation in ψ₂. The general solution for DNA dynamics is then written as

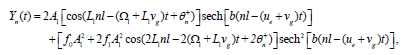(25)

where u_e stands for the velocity of the envelope. The corresponding solution is represented in Figure 3a, and clearly displays a breather solution. The same class of solution has already been obtained numerically in the previous section, and are found to be robust in DNA nonlinear models. Two classes of such waves have been discussed already, the ones describing the so-called DNA respiration and those related to the eye-like configuration usually observed in thermal denaturation experiments [12,25].

Figure 3: The panels show breather-like solitons in DNA for both the single (a), and mixed modes (b). The values of parameters are m=300 amu, s=0.04 eV/Ų, D=0.15 eV, a=6.3 Å^-1 and S=0.006 eV/Ų.

The mixed solutions

Solving the set of equations (15) depends on the sign of the coefficients [15,26,27]

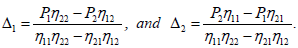(26)

In relation (26), one can notice the presence of the term 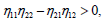which bring together the coupled solution and the MI analysis performed in the previous section. Breathing solutions for this model are found for Δ₁>0 and Δ₂>0, and is explicitly given by

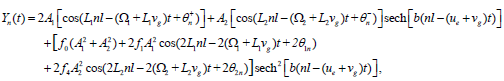(27)

where

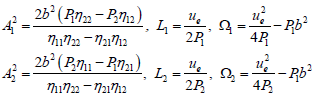(28)

The corresponding solution is plotted in Figure 3b. In comparison to the single mode case, the mixing of the counter propagating waves rather gives rise to a perturbed breather-like solution which seems to be more localized with noisy-like envelope. Of course, the reader should notice that from the beginning we did not include any noise to the model, rather these fluctuations in the breather solution are due to wave collision, i.e., at the point where the two counter-propagating waves mix. However, the features of that solution are expected to change for different values of the helicoidal coupling parameters S. This may be evident as the unwinding of the double helix implies a decrease of S. It was in fact shown that the resonant mode, the one supporting highly localized bubbles, is possible only when the helicoidal effects are weak [12,25]. Therefore, in the rest of the present work, the effect of small helicoidal coupling on the mixed solution is discussed. For S=0.002 eV/Ų, we have the solution of Figure 4a and for S=0.001 eV/Ų, the patterns of Figure 4b are obtained. When the value of S decreases, the compression of the hydrogen bonds reduces while the oscillations tend to become positive as shown in Figure 4b. We therefore have in mind to describe the fluctuating opening of the DNA double helix using the found mixed solution whose the features are described above. Under the action of RNA-polymerase, the hydrogen bonds linking bases in pairs are broken progressively to make the codon readable. The hydrolysis of ATP brings about energy that enhances the action of RNA-polymerase and therefore contribute to separate the two strands of DNA. In so doing, the effect of temperature is no more to be ignored through the action of ATP. We have simulated the opening of the molecule using solution (27), mainly at the point where the two counter-propagating waves collide, in order to picture the way environmental factors enhance DNA breathing. One of the waves describes the breathing of the double-stranded molecule, while the other stands for the biological factors that create and enhance bubbles in DNA. The subsequent bubbles are not different from those observed through DNA melting experiments. This shows and reinforces the fact that different waves are present in the process of DNA dynamics, and some are brought by the presence of enzymes around the coding sequences of DNA [28]. We therefore see how the bubble grows with decreasing S, in a fluctuating way, while hydrogen bonds are broken progressively as depicted in Figure 5. In Figure 5a, bubbles are created through wave mixing for S=0.002 eV/Ų. Progressively, as transcription factors modify the value of ξ the hydrogen bonds are broken and finally lead to the fluctuating transcription eyelike structure observed in Figure 5b for S=0.001 eV/ Ų. The action of RNA-polymerase through this work can therefore be seen as a wave that surfs the DNA helix and mixes with DNA breathing waves, a collision which yields fluctuating breather-like structures for the genetic code to be read.

Figure 4: The panels show plots of DNA strands oscillations under weak helicoidal coupling for (a) S=0.002 eV/Ų and (b) S=0.001 eV/Ų. Values of parameters are m=300 amu, s=0.04 eV/Ų, D=0.05 eV and a=6.3 Å^-1.

Figure 5: The panels display bubbles formation in DNA due to wave mixing (a) S=0.002 eV/Ų and (b) S=0.001 eV/Ų. Values of parameters are m=300 amu, s=0.04 eV/Ų, D=0.05 eV and a=6.3 Å^-1.

Wave interaction in the helicoidal PB model has been addressed in this work. Using the multiple scaling expansion, we have shown that the dynamics of counter-propagating waves can fully be described via a set of coupled NLS equations. MI Has been studied with emphasis on the features of single and mixed modes. In that context, the coupled mode has been found to expand the instability region, and numerical simulations have displayed trains of one-humped breathers for the single mode, and multi-breather trains for the coupled mode. Exact solutions have also been investigated for the two cases. Breather-like solutions have been found for the single mode, while highly localized fluctuating breather solutions have been derived for the mixed mode. We have further argued that the release of energy by ATP and the effect of RNA-polymerase could be assimilated to waves that collide with the weak DNA breathing in order for the molecule to be opened. However, recent developments have shown that when the hydrogen bond stretching is effective, the solvent molecules present in the DNA environment stabilize the molecule in the opened configuration [21,29,30] in order to prevent the molecule from re-closing. We should therefore modify the present model by taking accounts of these effects which could enrich our investigations on the most realistic profile of transcription and replication eye-like structures. In the meantime, the present work brings about the possible importance of multi-wave flowing in DNA double helix.