Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
+44 1478 350008
ISSN: 2161-0398
+44 1478 350008
Research Article - (2011) Volume 1, Issue 1
Background: In a normally developing eukaryote, information arrives at the cell membrane in the form of a ligand that binds to a protein receptor. This initiates a cascade of biochemical events causing one or more proteins to subsequently traverse the cell cytoplasm to the nucleus. This defines a communication channel. What does it accomplish? Method: The protein traversals transfer to the nucleus maximum Fisher information about the spatial and temporal coordinates of the ligand binding sites. This hypothesis implies a cell model of fast, largely-directed, protein movement dominated by Coulomb interaction with intracellular electric fields. It makes the following predictions: (1) Very high intracellular electric field strengths, typically tens of millions of volts/meter (2) A central role for negative charges added to proteins by phosphorylation, in promoting their Coulomb force-dominated motion toward the nucleus; (3) The dominance of protein pathways consisting of from 1-4 proteins, e.g. the RAF, RAS and MEK pathways; (4) A predicted fast response (2,800 proteins/ ms ) of cells to sudden trauma such as wounds; (5) A predicted 4nm size (9) for the EGFR protein. (6) Logic mechanisms in the nucleus for optimally deconvolving spatial and temporal binding site values from the inflowing messenger proteins. Results: Predictions (1-5) are supported by laboratory observations. Conclusions: Living systems achieve stably ordered and complex states by maintaining extreme levels of Fisher information. The attained order values increase from cancers to prokaryotes to eukaryotes to multicellular organisms. In eukaryotes this fosters maximally high protein flux rates at the nucleus which, in turn, optimize wired-in intranuclear logic mechanisms for processing this, and other, temporal and spatial information.
<The development and function of a multicellular living system requires a constant and accurate exchange of information among its cells. (Note: In this paper “cells” mean “eukaryotes” unless otherwise described.) In prior work [1-5] we have demonstrated that a stable highly ordered system, including functioning cells and multicellular tissue, must maintain a state of extreme Fisher information,
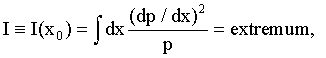 (1)
(1)
where p=p(x) is the system’s probability density law on random variable x. The law is assumed to be continuous, with a well defined first derivative. The first two equalities (1) define the Fisher information [6- 8] in the data about an unknown parameter x0 (such as protein position in (2) below) of a system p(x). This system is generally shift-invariant [6]. (Note: Information I is not the usual Shannon information [6], which is an entirely different measure.)
One fundamental reason for the extremum requirement (1) is to ensure system stability. An extreme value for I implies that its firstorder variation δI=0. Hence small environmental perturbations leave the information, and system, unperturbed.
A second fundamental reason for the extremum requirement arises from the requirement that, owing to natural selection, the system is highly “ordered” or “complex.” Thus, here the extreme value is a maximum. We concentrate on this case in most of the following.
The concept of the level of Order in a continuous system has been quantified [9,10] as level
R=(L2/8)I . (2)
Hence the order is linear in Fisher information I, the latter defined by Eq. (1). Also, L is the maximum chord length connecting two surface points of the system (effectively the diameter of the cell). Examples in [9,10] show that I and R also serve to measure the level of “complexity” in the system. (For example, a system with purely sinusoidal structure in all dimensions has a level of Order going as the square of the total number of sinusoidal wiggles in the system.)
We proposed [5] that for functioning eukaryotes, with their intrinsically higher requirements of order and complexity, the extreme information state should be a maximum. Here we quantify its value. For simplicity we use the terminology “information” I , “Order” R and “order” (no capitalization) interchangeably.
Much of the information exchanged between cells in living tissue is carried by secreted proteins (such as growth factors) that diffuse through the tissue and bind to specific receptors on the cell membrane (CM). The information is then carried from the CM to the nuclear membrane (NM) via messenger proteins. There are three components of information that are potentially available when a growth factor binds to a membrane receptor:
1. The presence of the ligand in the environment;
2. The time at which the ligand bound to the receptor; and
3. The location on the cell membrane at which the ligand arrived
Clearly the messenger protein, by entering the nucleus, carries environmental information that a ligand had bound to a receptor on the CM. In the conventional view of intracellular pathways, this is considered the entire amount of information transmitted. We propose that the principle of maximum (now) Fisher information requires the cell to also capture information regarding the time and position of the ligand binding. That is, we explicitly propose that mechanisms exist within the normal cell to convey to the nucleus maximum spatial and temporal information about ligand binding events.
Our hypothesis is that messenger proteins in functioning cells travel from the CM to NM over pathways conveying maximum Fisher information. This is specifically information I (x0) about the position x0 of a typical messenger protein as it strikes the NM, where x is the uncertainty in this position. Thus the total lateral excursion of the protein on the NM is
y=x0+x. (2)
The maximization hypothesis (1) will be examined in detail, and shown to be verified by the agreement of its predictions with laboratory observations.
This scenario of high information, i.e. low uncertainty, about the termination position on the NM implies, as well, low uncertainty (or high information) about position at the original ligand source position on the CM. This represents further stabilization of the system.
An information channel consists of a source particle, the medium through which it travels, and the receiver of the particle. Here the information bearing particle is a ligand that arrives at the cell and binds to a CM receptor. This typically initiates one or more secondary particle events to transmit the information through the cell medium, cytoplasm, to the nucleus (the receiver). Intermediate transfers of information usually occur as the activated protein binds to the next peptide in the chain, adding phosphates to specific amino acids on the protein. As an example a ligand binding to epidermal growth factor receptor (EGFR) on the cell membrane results in phosphorylation of several membrane proteins. In one pathway, phosphorylated RAS on the cell membrane initiates a sequence of kinases (RAF-MEK-ERK) that carry information from the CM into the nucleus.
This hypothesis requires control of messenger protein movements which is not currently part of the conventional model. That is, it is currently assumed that messenger proteins move through the cell cytoplasm by random walk. However, this would disperse the proteins throughout the cell so that information about their point of origin on CM would be lost, counter to our requirement of information maximization. We previously proposed [5] that efficient movement of proteins toward the NM will occur if random diffusion is replaced by highly directed (biased) random walk. This is accomplished by the presence of an intracellular electric field set up by the nucleus and possible mitochondria. Phosphorylation of messenger proteins will, in addition to altering their configurations, add negative charges to them. We propose that these charges enhance existing Coulomb interactions with the intracellular field and that these forces enhance the directed nature of the protein movement toward the NM. The theoretical and experimental details of this model are treated elsewhere [5].
Hence, what are the properties of its intracellular information pathways that allow the state of maximum information to exist? In particular:
Why are there 4 proteins (i.e. RAS, RAF, MEK, ERK) in the MAPK pathway that carries information from the CM to the NM? Why not 1 or 6 or 8? Specifically, why does the cell go to the trouble of passing on information from one constituent EGFR protein to the other when it seems it would be easier and more efficient to just have one protein messenger carrier? If more than one protein in the sequence is valuable why stop at 4, why not have a larger number? Why are proteins, which are large structures that are relatively “expensive” to synthesize, used as carriers rather than smaller molecules such as individual amino acids or nucleotides? These are taken up below.
We frame the information hypothesis as a mathematical principle of cell development. Then, what protein pathway accomplishes a maximum information transfer rate from CM to NM? And what is the level of this information?
Let ta be the traversal time of a protein from CM to NM. It is shown at Eq. (S12) of Appendix S that, for a given flux rate F (number/areatime) of proteins at positions y of the NM, the information level
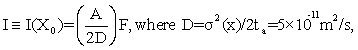 (3)
(3)
is attained. Here D is the diffusion constant in cytoplasm and A ≈π a2 is the cross sectional area of the nucleus. The spatial information (3) thereby decreases with increasing diffusion D, which makes sense, and increases with both the nuclear area A and flux rate F. These are also intuitively correct trends. Eq. (3) also shows that, for given values of A and D, channel capacity value I=max is attained when F is maximized. We first observe how F varies with values of the Debye-Huckel parameter k0; and then use (3) to compute I from this.
Using Eq S6, Eq S7, and Table 1, the flux F is plotted as a function of k0 in Figure 1. The cell is simply modeled with spherical surfaces in Figure 2.
| CM radius r0 | 5 micron |
| NM radius a | 3 micron (Note:α/r0 ≈ 60% for mammals) |
| Cytoplasm dielectric const. | ε = 60ε0 = 7.1×10–10F/m |
| Thermal energy kBT | 4.14x10–21 J |
| Positive charge on nucleus QNM | ≈+0.3×10–11C (Coulomb) |
| Viscosity η of cytoplasm | ≈10–13 (water) |
| Reynolds number R0 | 462×(0.4 nm) |
Table 1: Parameters of the cell.
The curve for F shows a strong decrease (by orders of magnitude) once k0 is greater than roughly 4.0x106 m-1. Also, of key importance is that F goes smoothly to zero at both small k0 and large k0 . This implies some definite in-between value k0≡kmaxfor which F = max. ≡Fmax. However, uncertainties in values of the cell parameters do not allow the precise point (kmax, Fmax) to be found. Instead, from the figure
Fmax≈1017 for k0=kmax≈(1.0,1.4,1.7or 2.0) x 106 m-1. . (4)
Value k0=kmax≈1.7) x 106 m-1is central to this range of possible values kmax. Thus, since protein number n=k0 2 x 10-12m2 (by Appendix S) the maximum value is approximated by pathways containing either n=1,2,3 or 4 types of protein.
Our overall criterion of cell development is Eq. (1), that information I(x0) =max. Using Fmax from (4), D from Eqs. (3), and by A≈πa2=28.3μm2 from Table 1, Eqs. (3) give
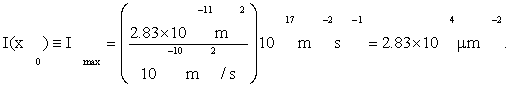 (5)
(5)
Then by Eq. (5), the Cramer-Rao inequality [2,6-8] gives
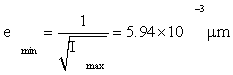 (6)
(6)
Or 5.94nm , as the minimum possible root-mean square (rms) error in knowledge of the protein position. Relative to the NM size 2a=6μm, this is an error of 0.1%, quite small. Even more remarkably, this small error is attained every 0.01 sec by a protein cloud (or ‘scaffold,’ see Appendix S).
The value (6) of emin=5.94nm represents the total uncertainty in a single protein position x0 at the NM on the basis of maximum information. The calculation took into account protein density and, hence, protein size. Of course, at present it is not known how the nucleus estimates the ideal position x0 of a protein. However, it must depend upon (at least) both (a) observed position y [see Eq. (2)] and (b) size values dm of the protein. These may be regarded as random samples from two probability laws: (a) on the uncertainty x of the center of gravity of the protein; and (b) the uncertainty d in the size of the protein, arising out of random protein foldings en route. Let both random variables x and d be Gaussian distributed, the latter with an rms uncertainty of value dp. This also represents the effective size of the protein. Since the processes governing x and d are statistically independent, the total information Imax is then the sum of the two.
It results that the total information acquired by the NM from each protein detection event has a two-fold contribution the latter from (5).
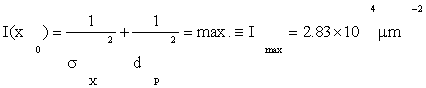 (7)
(7)
But to find the protein size dp we need another relation: There are two independent and additive contributions, x and d, to the positional error. Then by (6) its variance emin 2 obeys
emin2=σx2+dp2=3.528 x 10-5μm2 (8)
We regard this as a Lagrange constraint on the extremum condition (7). These together give a unique solution for the unknowns dpand σx,
dp= σx≈4.2nm. (9)
As a reality check on this solution, the extension of an EGFR protein is about 3nm , close to this value. It follows that, on the basis of maximum information and conservation of resource, the largest permitted messenger protein is about the size of the EGFR. This is a further verification of the hypothesis (1) of maximum information.
The nucleus can process detected protein positions no more rapidly than the traversal time, a predicted value ta=0.01s for the proteins. The quality of each such output estimate x0 then grows with the net number Na of detected proteins per traversal time ta. How large is Na?
The arrival flux of proteins about the position x0 on the NM was found at (4) to be Fmax≈1017 proteins/m2s=105 proteins/μm2s. Multiplying this by the NM area of about πa2=28μm2 gives the total arrival rate, about 2,800,000 proteins/s. Or equivalently, the nucleus processes Na = 28,000 data consisting of arrival locations every traversal time interval ta=0.01s =10ms. By the additivity of information I , the presence of large amounts of data lead to higher information. And then, by (6), these beget smaller errors in the parameter to be estimated, here the NM location x0. These smaller errors are computed in the next subsection.
The preceding numbers appear to be consistent with clinical data: Cell response times of 10-100ms following trauma injury have been measured [11]. In fact our mean traversal time per protein ta=0.01s =10ms meets the fastest such measured response time to trauma and, so, provides a “worst case scenario” for the theory.
But the total accuracy in approximating ideal position x0 is even better than the small value (8) of mean-squared error. There are Na = 28,000 data locations yn to average over, even in the most demanding case of a required response time of 10ms. Suppose that the mean value of these sample locations (called the “sample mean”) is taken as an estimate of the true location x0. A “sample mean” incurs an rms error [6] of
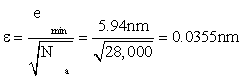 (10)
(10)
after using (8) to get emin. Sure enough, this is about 1/200 the error emin in one data location. But is this error ε small enough to accurately locate the position of a base pair of DNA?
Each such has a length of about 0.33nm. Therefore the relative error in locating it is, by (10), 0.0355/0.33=0.108 or about 11%. An additional constraint that evolution has succeeded in building into the estimated location is that each such base pair must be a codon, of which there is but a limited number (from 4-6 depending upon scenario, as next). This can only improve overall accuracy to better than the 11% figure.
In summary of this section, the requirement (1) that the positional information of the messenger proteins is maximized leads to the following predictions:
(i) Information levels I(x0)≡Imax=2.83 x 104μm-2; with
(ii) maximum accuracy -- error level emin=5.94nm in a single protein position, or a relative error of 11% in locating the position of a base pair of the protein in even the fastest required response time (to trauma) of 0.01s; and
(iii) maximally high flux -- 28,000 protein arrivals within the fastest required response time (to trauma) of 10ms.
But when is maximum accurate positional signaling needed?
An example of a need for accurate positional signaling is seen in developmental biology. Morphogenic gradients direct organ and tissue formation in fetal development. This requires normal cells to recognize and accurately measure a gradient of morphogens across its diameter. For example, TGF β (transforming growth factor beta) signaling [12,13] gradients are used to define the locations and shapes of tissue boundaries. During activation protein signaling, an extracellular TGF β ligand binds to its type II receptor on a cell CM. This enables a type I receptor to join the complex. The type II receptor then phosphorylates the type I receptor, which, in turn, phosphorylates an SMAD2 protein. This, in turn, associates with an SMAD4 which enters the NM. Detection and measurement of variations in concentration of TGF β around the circumference of the cell will require that the ligand binding position, y, on the cell surface to correspond with high accuracy to some NM position x0. This corresponds to high information I(x0) [see Eq 5)] in positioning of the SMDAD4 proteins on the NM, and therefore welldefined tissue boundaries.
The hypothesis (1) of maximum Fisher information I in protein communication between CM and NM has led to five predictions, which can be compared to published empirical observations.
1. The prediction of intracellular electric field strengths on the order of tens of millions of volts/meter. Recent work [14] by Tyner et al using nanoparticles measured intracellular electric fields in the range of - 3.0 x 106 to -5.0 x 105 V/m.
2. The central role played by phosphorylation in promoting the directed, Coulomb-dominated motion of the protein toward the nucleus. The predicted rapid motion of phosphorylated proteins from the CM to the NM has been observed [5].
3. The dominance of protein pathways consisting of from 1-4 proteins, e.g. the 3-protein pathways RAF, RAS and MEK. In fact all known intracellular pathways consist of from 1 to 4 proteins
4. A cell response time to sudden stimulation is estimated to be remarkably fast, in the range of 10 to 100 μsec. This is, in fact, consistent with the measured response rate [11]. The estimated NM flux messenger protein flux for optimal information processing is 2.8 x 106 proteins/sec. We can find no empirical data to support or refute this prediction although we note that a eukaryotic cell is estimated to contain 8 x 109 proteins so the predicted flux, while large, still represents flow of less than 0.0005 of the total protein content.
5. The prediction (9) that the optimal size of messenger protein is about 4nm in size. This matches the size of most messenger proteins.
Living systems are subject to Darwinian selection that optimizes fitness. We have previously demonstrated that this optimization process is dominated by a trade-off between energy availability and information utilization. The latter can increase the Order (2) and complexity of a living system, but only at a cost of increased energy requirement. We previously found [1-5] that cancer, having lost functional ability, attains a state of minimum order and complexity. Likewise, prokaryotes, which lack specialized energy producing organelles (i.e. mitochondria) will optimize their fitness by maintaining a minimum amount of information necessary to maintain proliferation. This minimum state is an extremum and, hence, ensures maximal stability to first order perturbations. However, as shown by Lane and Martin [15], eukaryotes, which contain mitochondria, have much higher energy capacity. We have shown that under these conditions, living systems will typically move toward an information maximum. Thus, there is a predicted hierarchy of information states:
From lowest to highest these are of cancer, prokaryotes, eukaryotes and multiple-celled organisms.
Here we examine the consequences of our prediction that mammalian cells will maintain a state of maximum information, with a particular focus on the critical information transfer from the cell membrane to the nucleus. The conventional model of cell development pathways concerns itself with the fact that ligand binding occurs on some membrane receptor. This is irrespective of when and where the binding takes place. By comparison, our principle of maximum information predicts that proper cell development depends critically upon the degree of randomness, i.e. statistical spread, in these position and time values. The smaller the spread the greater the information.
Accordingly, we have built such knowledge into a new model of information pathways. By the model, temporal and spatial information is transferred from the CM to the NM via directed diffusion. The directed nature of the flow is governed by Coulomb interactions between an intracellular electric field and the negative charges on phosphorylated messenger proteins. We demonstrate that predictions of this theoretical model are consistent with multiple experimental observations.
An explicit prediction is that such maximal nuclear organization will allow it to optimally decode the spatial and temporal information that is input at the CM via internal mechanisms (that are as yet unknown).
A past use [16] of our principle of maximum Fisher information was derivation of the famous quarter-power laws of allometry
y=Cnmn/4. (11)
Here y is a biological trait, such as the metabolic rate of a eukaryotic creature of mass m, Cn=const,. and n is an appropriate integer n=0,±1,±2,… For example, n=+3 for the metabolic rate y of the creature. Thus the creature’s metabolic rate grows with its biological mass, and at a slightly slower rate than linear. As another example, n=-1 determines a creature’s RNA density, so that RNA density decreases (now) with mass, although quite slowly.
The authors acknowledge support form the National Cancer Institute under grant 1U54CA143970-01.