Change detection techniques and algorithms are critical to many computer based applications such as remote sensing, video surveillance and medical imaging. These techniques have witnessed continuous development over the past decade, and as a result, there are now various algorithms, methods, and automated systems available.

In particular, automating the identification of the changes in medical images taken at different times is of great relevance in clinical practice. Magnetic resonance imaging (MRI) datasets may for example include multiple sequences, each consisting of many images obtained for one exam needing comparison with the immediate previous study or multiple prior studies. The size of datasets that radiologists are dealing for computed tomography (CT) or MRI can be hundreds or thousands of images for each time point.

The main challenge of change detection algorithms in medical images is to detect disease-related changes while rejecting clinically irrelevant changes induced by noise, mis-alignment, and other acquisition-related artifacts, such as intensity and inhomogeneity [1].

Radiologists must visually interpret serial studies to identify changes including those caused from patient repositioning and identify and reject certain artifacts. Some of the challenges of side-byside presentation approach include scanner software and hardware related changes, separation of acquisition changes from disease related changes, information overload, the inability to detect changes in objects or scenes being viewed, the inability to make comparisons between two scenes, and satisfaction of search. Although change detection is relevant to all imaging modalities such as MRI, CT, and sonography, in this paper we focus mostly on MR images of the brain.

General reviews on change detection algorithms and especially in video surveillance and remote sensing can be found in Refs [1-4]. For medical imaging field, Patriarche et al. [5] presented a detailed review of change detection methods in serial imaging studies of the brain and also made the case that automated registration and change detection systems would be a great help for the radiologists to correctly interpret data. In addition, Lladò et al. [6] provided a review of the methods and algorithms for detection of multiple sclerosis lesions (MS) in serial MR images of the brain.

Several studies made during the last decade are mostly statistical based. Bosc et al. [7] presented an automatic change detection system for serial MRI with applications to follow-ups of multiple sclerosis. It is based on the use of multimodal information for change detection, generalized likelihood ratio test, and nonlinear joint histogram normalization. The performance of the algorithm is low when noise is not-stationary. The authors in Refs [8-10] presented a more complete automated change detection system which can improve efficiency, accuracy and reader agreement. They found that implementing a scientifically useful tool is most clinically viable when it is efficiently integrated into clinical work flow. In Ref [11] authors used a general nonparametric statistical framework based on local steering kernels. However their method requires accurate co-registration of input images as a pre-processing step.

The focus of our work is to identify disease related changes in three dimensional sequential MR images and our objective is to develop a change detection system that can identify related changes in the presence of noise, misalignment and other imaging acquisition related artifact. The idea of our solution to change detection problem is utilizing local dictionary learning techniques to identify those changes in the Principal Component Analysis (PCA) transform space. Our methods are based on background modelling and dictionary learning techniques, inspired by the following papers [12-16].

Recently, background modeling and sparse representation methods have been used successfully in video surveillance [14,16]. In Ref [13] background subtracted images are recovered using compressive sensing (CS). Work of Ref [17] proposed the use of principle component pursuit method to detect foreground changes in video surveillance. The work is based on low-rank and sparse decomposition of image matrices. Robust principal component analysis has applications in many other areas, such as face recognition, etc. Authors in Ref [15] use robust dictionary learning to solve the background subtraction problem. Their approach appears to produce a better dictionary than more traditional K-SVD algorithm [16]. However, the assumptions for sparsity must hold. Work in Ref [15] addressed mis-alignment in change detection problem by employing a series of sparse optimization problems. However, their method only works well for highly sparse images, such as SAR images that are much sparser than most medical images. Authors in Ref [12,14] used eigenfaces for face recognition and pattern recognition by finding the principal components of the distribution of faces, or the eigenvectors of the covariance matrix of the set of face images.

In previous publications, we extended primary work in the area of background modeling and dictionary learning techniques and developed three variant methods [17-20]. Our first algorithm, (Adaptive EigenBlock Dictionary Learning (AEDL)) [17] , performs image registration locally to capture the local spatial changes in the test image using a series of local sparse minimization processes and the knowledge of compressive sensing. The method takes a pair of images as input, and gives two images as output: the recovered sparse image aligned with the second one and the image of detected changes. The reconstructions of overlapping blocks using L1 minimization algorithms make the AEDL algorithm computationally expensive. To reduce the running time of the algorithm, we designed the second algorithm, EigenBlock Change Detection (EigenBlockCD) [18] , which uses the L2 norm as a similarity measure to learn the dictionary. The method takes two images as input and automatically produces an image which contains only clinically related changes. Both, the AEDL and the EigenBlockCD algorithms ignore insignificant changes due to patient’s position, noise, and other acquisition related artifacts, when these unrelated disease changes are within a small neighbourhood. To account for large sizes of insignificant changes, i.e., large shifts and rotations, we designed second versions of the two algorithms, the AEDL-2 and EigenBlockCD-2 by adding a co-registration step at the beginning [19,20].

The motivation for this paper comes from two main reasons: 1) MR images are originally volumes in three dimensional space and 2) the patient position changes, i.e., rotations and translations, are also three dimensional. In fact, in many cases when we compare images pair by pair they may not be exactly of the same anatomic location because of the rotations and shifts. This made us believe that extension to 3D will actually increase the accuracy of change detection of medical images.

We reviewed some existing work in this area. In methods based on measurement sampling [24] a radiologist measures the maximum diameter and the maximum corresponding perpendicular of a tumor, or computes the maximum area of a tumor [21,22] to assess the progression or regression of the disease. One of the drawbacks of such methods is the ability to detect small changes, because of the difficulty of radiologists to reach a consensus. In some volumetric methods, the global volume of each anatomical tissue of interest at each acquisition time is calculated, and the results are subtracted [23,24]. This increases the uncertainty and error is accumulated when regions are large. Two other volumetric methods [25,26] identify the tumor first and then compute its volume each time. The growth rate is computed as a ratio of the difference between the computed volumes and time interval. The intensity-based methods [27] initially align two volume sets of data to a fraction of the linear dimension of a voxel, and then utilize simple differencing of the aligned source images to find intensity differences due to evolving lesion. In 3D methods, registration is a very important component of medical image analysis. The impact of miscoregistration is discussed in Ref [28] concluding that the presence of registration errors in the images may affect the accuracy of change detection. A thorough review of how the choice of the cost functions and the number of transformational parameters effect the quality of registration is discussed in Ref [29,30].

Change detection methods mentioned above present an improvement over simple visual inspection and classical statistical approaches. However, most methods require many preprocessing steps such as registration before using the core algorithm [8-10]. Some methods require spatially sparse images [15] while the others require a large database of images [14,16]. On the other hand, the pathological changes in brain tissue may also affect the accuracy of change detection. In this paper we extend the EigenBlockCD-2 and AEDL-2 algorithms to detect the changes of 3D volumetric data. MR images are originally volumes in 3D as shown in Figure 1. Similar to the 2D case, we consider the 3D volumes of the same anatomical objects taken at two different times. The obtained image slices are generally misaligned due to patient position and other acquisition related artifacts. We define the problem of change detection in 3D and present the 3D AEDL-2 and 3D EigenBlockCD-2 algorithms for volumetric data. The algorithms include two steps: 1) the 3D global alignment process and 2) a detection step of 3D change detection algorithm. The flow chart of the algorithm is provided in Figure 2. We show the performance of the 3D EigenBlockCD-2 algorithm with real 3D brain MR images. The changes detected by our algorithm are confirmed by the radiologist’s diagnosis.

Figure 1: An illustration of a 3D MR volume of a brain.

Figure 2: Flow Chart of 3D EigenBlockCD-2 algorithms for volumetric data. The input are two MRI volumes of the same patient taken at two different times, named reference and test volume respectively. The processes is composed of two steps: 1) the 3D global alignment process, and 2) detection step of 3D change detection algorithm. The output is the test volume with overlaid changes.

Most existing methods such as those in image surveillance and face recognition [12,14-16,31] learn the dictionary by using training samples from a database of images. In our algorithms we use the reference volume blocks to learn the dictionary. Our model is a block based dictionary which captures only local disease related changes and ignores changes due to the patient positioning, etc. It uses overlapping blocks to reduce image block artifacts.

The rest of the paper is structured as follows. In Section 2 we give the problem formulation and notations to change detection problem for volumetric data, with a solution to change [32-35] detection problem for volumetric data presented in Section 3. We present an application to real MR volumetric data in Section 4, followed by the discussion and conclusions as given in Section 5.

Problem formulation and notations

MR imaging provides a very detailed anatomical view of soft tissues including the human brain and is the best among all structural imaging modalities. MRI can be used to detect a variety of brain disorders including brain tumors, multiple sclerosis, stroke etc. An original MR image produced by MRI machine software depicts the anatomic variations of signal intensity in thin slices as shown in Figure 1. As a result, a set of images, each describing a slice of the object (brain, etc), is obtained and stored by MRI software in a special format.

Geometrically speaking, a 3D image obtained from MRI scans is a volume of voxels. A voxel or a volume element is the 3D corresponding term for a pixel in 2D image. An automated change detection system compares two 3D volumes from a patient taken at two different times.

Let V₁, V₂,…… Vn represent volumes of size 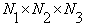of the same anatomic location, taken at different times, t1,t2,…tn respectively. Let V_cd (1,2), V_cd (2,3),….., V_cd (n-1,n) represent the true changes between should read “V₁ and V₂, V₂ and V3;…;Vn-1 and Vn”, where true changes are not caused by patient position change or noise. Let Vs(i,j,k), s=1,2,…,n, i=1,..,N1,j=1…,N2, k=1.., N3, be volume intensity of a voxel at i -th row, j -th column of the k -th slice.

The question is: Can we automatically detect true changes while ignoring the changes that are not clinically relevant?

Definition of change detection of a volume set

Let the set of input volumes of the same siz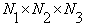e, , be 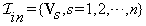, where V_s is the volume corresponding to time t_s. We define the change volume set by V_out

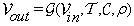
where:

• G: The mathematical model.

• V_in: Input volume set.

• T: A set of transform functions, i.e., change of basis functions, such as those of wavelet transform, Fourier transform, etc.

• C: The cost function to be minimized using a similarity measure, which compares and checks feature changes between V_t1 and V_t2.

• ρ: Similarity measure, i.e., distance measures such as L₁, L₂, L_(2,1), cosine similarity, similarity maps.

• V_out : Output, a set of images with changes between V_s-1 and Vs that is,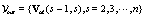

For simplicity, we aim to detect changes between two consecutive volumes, V₁ and V₂, initial (reference) and follow-up (test), taken at two different times. Similar to Equation 1 we define V_cd as the volume of changes between V₁ and V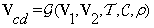₂

(2)

where: G is the mathematical model, V₁, V₂ the input images of the same size, T a set of transform functions, C the cost function to be minimized, ρ similarity measure, and V_cd the output volume or the volume of changes between V₁ and V₂.

An automated change detection algorithm between two volumes, V₁ and V₂ takes two volumes as input and produces a change volume, V_cd as an output. A change detection algorithm should also be able to identify whether the change is considered significant (important) or insignificant according to a particular application, therefore the algorithm should maximize the number of significant changes found, while minimizing the insignificant ones. Furthermore, the output should be the one that is the closest to the real (true) change volume, from all the change volumes determined. The problem can be formulated as:

Given V₁ and V₂ ,find the optimal G, T, C and ρ used in the algorithm to compute V_cd . Desirable solutions require an automated system to:(1) Detect changes in medical volumetric data which are subtle and disease related, while rejecting changes caused by patient position, noise, and other acquisition related artifacts, (2) reduce the quantity of data presented to the radiologist, and (3) present changes in the way that match human visual system, are easy to read, see, and understand.

We extend our 2D change detection algorithms [17-20] to 3D volumetric data. The 3D change detection algorithms are named as 3D EigenBlockCD-2 and 3D AEDL-2. The new algorithms take into consideration a new transformation model, an interpolation step, a similarity measure, and an optimization method.

We make similar assumptions as in the 2D case. That is, two consecutive volumes differ from one another due to disease related changes, shifts, rotations and noise. During this time interval most blocks from the reference volume have undergone a few disease related changes. Most voxels of the volume at time t₁ will appear again in the second volume V₂ either at the same or a nearby location. This means that a block from the reference volume, with some structure, would appear again in the test volume, having a similar structure, either at the same location or within the neighbourhood. In other words, the background of each block from the test volume can be learned from the reference volume blocks. Therefore, the background of a block from the test volume, located at (i,j,k), can be learned from the reference volume blocks located in some Δ neighborhood of (i,j,k).

Let V₁ and V₂ represent volumes of the same anatomical structure corresponding to times t1 and t2 respectively. V₁ and V₂ are referred to as the reference and the test volume respectively. Let bijk be a block of size (2δ+1) × (2δ+1) × (2δ+1) in the test volume centered at voxel (i,j,k) where parameter δ is a positive integer, representing the radius of the bijk block. There are (2δ +1)³ voxels in bijk. Let aijk be a block in the reference volume of the same size as bijk centered at the same location. It follows from our assumptions that for a test block bijk, we can define a neighborhood of length Δ and centered at position (i,j,k) in the reference volume, such that the background of bijk can be learned from the blocks within the neighborhood Δ.

We introduce the following additional notations:

The block bijk from the test volume is centered at voxel (i,j,k) and it is referred to as the

Block of Interest For simplicity we denote it by b

The Δ neighbourhood of (i,j,k) voxel, denoted by B in reference volume is called the Inquiry Block

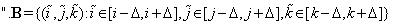
D is the set of all blocks al of the same size as the block of interest b from the inquiry block B.

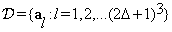
Blocks a_l from the inquiry block are referred to as the ”Training Blocks”. Blocks a_l are of sizes (2Δ+1)×(2Δ+1)×(2Δ+1) and centered at (p,q,s) where .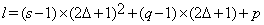

Let 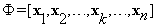be the dictionary formed by stacking all the training blocks al to column vectors x_l. Figure 3 shows two 3D volumes, a block of interest b, stacked as a column vector y from the test volume and the training blocks a_l stacked as column vectors x_l. Training blocks a_l are extracted from the inquiry block B. Remarks: (1) The dictionary Φ is used in our model to learn the background of the block of interest, (2) the dictionary Φ is adaptive in a sense that the columns of Φ get updated every time we move to a different block of interest in the test image.

Figure 3: An illustration of two 3-dimensional volumes. (a) and (b) stack of slices representing the reference and the test volumes respectively, (c) shows a block of interest b from the test volume, b is stacked as a
column vector y, its inquiry block B from the reference volume, with many overlapping training blocks aj which are then stacked as column vectors xj of the dictionary Φ, and γ represents the coefficients of linear decomposition of vector y over Φ.

Let 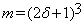and 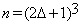.Then, the block of interest b and each training block al are of sizes 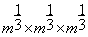. The inquiry block B is of size .

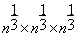To achieve a more precise alignment in the 3D case we need to generate more slices between the existing ones. The 3D anatomical data sets we have used in our simulations are of size 384 × 384 × 20, i.e., 20 slices of size 384 × 384 each and with a slice thickness of 5 mm. Between every two slices we insert four slices by applying cubic spline interpolation, thus, obtaining a volume of size 384 × 384 × 96. In the co-registration step, our algorithm aligns the baseline volume with its follow-up volume first. After the two volumes are aligned, the algorithm extracts the 20 original slices from the volume that hasn’t been transformed and the corresponding 20 aligned slices from the transformed volume.

From our assumptions, the block of interest is learned from training blocks in the inquiry block. Each block of interest can be sparsely approximated using a linear combination of a few blocks from the reference volume over a dictionary Φ by the following equation:

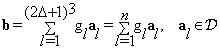(3)

where .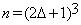

Blocks al and b are stacked as m×1 column vectors x_l and y, respectively, where and δ is a positive integer representing the radius of these blocks. Equation (3) can be written as: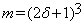

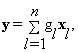(4)

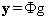(5)

where:

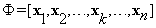
And 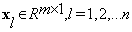obtained by stacking the entries of the training block al, i.e., 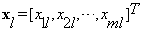, 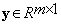is the vector representation of the stacked block of interest, i.e., 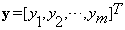and 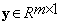is the vector of coefficients in Equation (5), i.e., 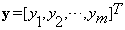From the assumption that the vector of coefficients γ is sparse, our method seeks to solve Equation (5) for the sparsest γ. Let us consider the following minimization problem:

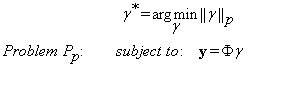(6)

where 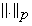represents the L_p norm. To account for noise Equation (7) can be written as:

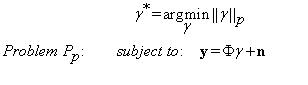(7)

Next, we discuss the co-registration step followed by change detection step. In the end we provide a summary of our algorithms for volumetric data.

Initial global alignment of 3D volumes

The reference and test volumes are generally not aligned. For example, Figure 4a and 4b show that the tenth slices from the reference and the test volumes are not aligned and do not show the same anatomical structures, meaning that they do not represent pictures of the same scene taken at different times. To accurately detect the relevant clinical changes, we first perform the global initial alignment between the reference and the test volumes. After the co-registration step, the tenth slice from the test volume and its corresponding tenth transformed slice from the reference volume are aligned as shown in Figure 4a and 4c, respectively. The algorithms used in 2D [17-20] can be easily extended for 3D volumes which we present below.

Figure 4: (a) and (b) The reference and the test volumes of patient data (T2- weighted), MR volumes of a brain scanned in 2011 and in 2013, respectively. Note the lack of initial alignment between volumes. (c) The reference volume is now aligned with the test volume.

The co-registration problem finds the transformation parameters that best align the two volumes by determining a transformation space and a cost function that quantifies the quality of alignment. In our 3D registration problem, the transformation space includes six rigid transformations with six degrees of freedom, i.e., three parameters for translations and three for rotations. Figure 5 illustrates the three rotation parameters to be determined by the co-registration step of our algorithm. As with the EigenBlockCD-2 algorithm, we use the L2 norm as the cost function. The minimization of the cost function finds the optimal parameters for which the static and large anatomical structures such as the skull, the eye balls and CSF between the two consecutive volumes are aligned as much as possible.

Figure 5: An illustration of the three rotation parameters (α,β,γ) to be determined by the 3D AEDL-2 and 3D EigenBlockCD-2 algorithms during the co-registration step.

Let T be a set of transform functions, P a set of transformation’s parameters and C the cost function to be minimized. For any two 3D volumes of the same anatomical part, the registration problem finds six parameters such that the two volumes are to be geometrically aligned after transforming one or both volumes using these parameters. The cost function checks the accuracy of the alignment, that is, maximizing the accuracy of the co-registration by minimizing the cost function, minimizing the norm of the difference between one volume and the second volume transformed. The two volumes represent the 3D MR volumes of the same patient and the same anatomic location taken at two different times.

Suppose that the reference volume has to be rotated by angles α, β and γ to be aligned with the test volume. This is equivalent of rotating x, y and z-axis by angles α, β and γ. In Figure 5, if line M (in green) represents the intersection of the xy-plane (in blue) and its rotated xyplane (in red), then the angle α is the angle between the x-axis and the line M, representing the rotation around z-axis. Angle β is the angle between the two z-axis, (in blue and red), and γ is the angle between the new x-axis and line M. The co-registration problem can be written as a minimization problem:

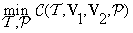(8)

Where:

• V₁, V₂ represent the two volumes to be aligned.

• C is the cost function in the minimization problem, i.e., the L₂ norm given by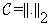

• T is the set of transform functions; in our case T is any composition of transform functions from the set {T,R}, where T and R are translation and rotational transform function sets.

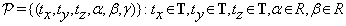
• and 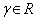, is a set of 6-tuples (t_x,t_y,t_z, α, β, γ)

representing the six parameters needed to align the two volumes, i.e., the sizes of the three shifts in x, y and z directions and the sizes of the three rotational angles, α, β and γ.

Let V(i,j,k) represent the intensity of a volume voxel at location (i,j,k). Volume V is of size 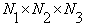The translation and the rotational transform functions can be applied to each volume voxel as follows:

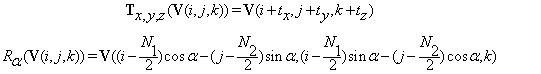
The formulas for 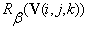and 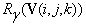are obtained in similar fashion. In our initial co-registration problem we consider a composition of all the six transform functions: 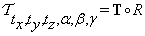, where 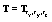and 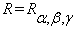. In matrix form 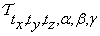can be written as:

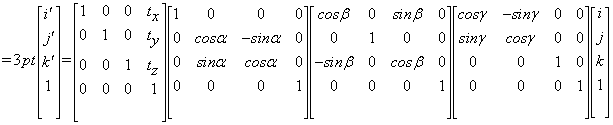
where (i,j,k) and (i’,j’,k’) represent the original and the transformed coordinates, respectively. Then, the co-registration problem in Equation (8) can be written as:

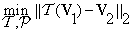(9)

The problem seeks to find a 6-tuple 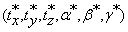that minimizes Equation (9):

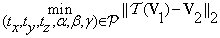(10)

where 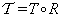, 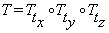and 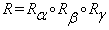. Equation (10) can be written as:

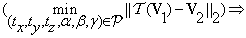(11)

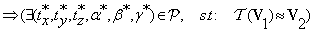
The 6-tuples 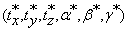are automatically determined by the co-registration step. The three translation parameters have integer values and are determined directly without any input. On the other hand, the rotation parameters are selected from a range of given angles with integer values, i.e., θϵ [-10°,10°]. The co-registration step is sufficient if the difference between the original test and the transformed reference volumes is no larger than 2° angle about each axis. It derives that there are only finite values ϵ[-180°,180°] for the rotation parameters.

Remark: For two consecutive volumes, the insignificant changes due to affine transformation, i.e., translations and rotations, are bounded. More specifically, the sizes of the shifts cannot be greater than half of the maximum of each edge of the volume. That is, 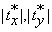and 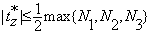, where N₁, N₂ and N₃ are number of rows, columns and the number of slices in a volume. Therefore the sets of the three translation parameters are finite. Similarly, the sets of the rotation angles as integers from [-180°,180°] are finite. This means that the minimum in Equation (11) is always reached.

Detecting changes

In this step, the change detection problem becomes an optimization problem. The dictionary Φ is formed by stacking training blocks as column of Φ:

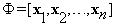(12)

The dictionary is composed of reference volume blocks and has high level of redundancy because many voxels are included in more than one block. We thus use PCA to reduce the dimensionality of the dictionary dataset and eliminate such redundancy, and to decrease the computational time. Also, PCA is used as a feature extraction tool by emphasizing most significant features within each local dictionary.

The initial problem (7) in eigen-subspace can be now written as:

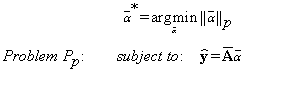(13)

case of using the 3D AEDL-2 algorithm, the background of the block of interest is modeled by solving the minimization problem (P₁):

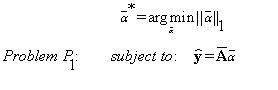(14)

Using the solution 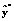of Equation (14) the 3D AEDL-2 algorithm computes 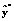, i.e., an estimate of the projected background of 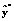in the selected eigen-subspace, by solving the following linear system:

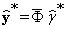(15)

Therefore, we reconstruct y* , the background of y in spatial domain, by solving the following equation.

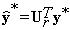(16)

We observe that the matrix of eigenvectors Ur is full rank and the number of rows is greater or equal to the number of columns, m ≥ r. Therefore, the (left) pseudo inverse of 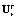exists. Note that the left pseudo inverse of a matrix V is: 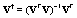Hence, the left pseudo inverse of 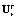can be computed as 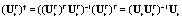The background in the spatial domain is then given as:

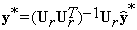(17)

To compute the background y* of y the 3D EigenBlockCD-2 algorithm finds the best approximation to y in the reference volume, that is, a vector xl from dictionary Φ that minimizes the residual error:

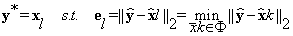(18)

Whe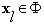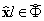re , where 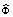is the projected dictionary Φ onto the eigen-subspace. The residual error block with changes is computed as:

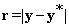(19)

The foreground block F containing only the significant changes is computed as:

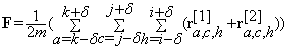(20)

where, is the block r centered at voxel (a,c,h) when the background of the block of interest in the test image is learned from the training blocks in the reference image, and similarly, 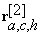is the block r centered at voxel (a,c,h) when the background of the block of interest in the reference image is learned from the training blocks in the test image. The change volume between the baseline and its follow-up is:

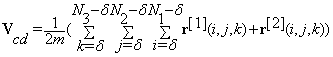(21)

Finally, the output is thresholded to further eliminate the noise and the false positives. The output voxels greater than the threshold are considered as clinically relevant changes. The threshold is automatically selected in such that it throws away only a small percentage of the change voxels, i.e., in a range from 1 to 3%.

We tested the 3D EigenBlockCD-2 algorithm with real MR volumes. Selected images and results are shown in Figures 6-8, while the completed set is shown in Figures 1-3 in Appendix A.

Figure 6: Selected slices from a real T2-weighted MR of a brain volume taken in 2011 and its follow-up in 2013. (a) and (b) Reference and Test volume, (c) Reference aligned to test after six affine transformations, (d)
and (e) change volumes via differencing before and after the co-registration step respectively done by our algorithm, and (f) change volume via the 3D EigenBlockCD-2 algorithm. Note the new maxillary sinus mucosal thickening shown in green in Figure.6 (f).

Figure 7: Slice #12 of real T2-weighted MR of a brain volume taken in 2011 and its follow-up in 2013. (a) and (b) Reference and Test volume, (c) Reference aligned to test after six affine transformations, (d) and (e) change volumes via differencing before and after the co-registration step respectively done by our algorithm, and (f) change volume via the 3D EigenBlockCD-2 algorithm. Note the new small bilateral foci shown in green in Figureure (f).

Figure 8: Slice #14 of real T2-weighted MR of a brain volume taken in 2011 and its follow-up in 2013. (a) and (b) Reference and Test volume, (c) Reference aligned to test after six affine transformations, (d) and (e) change volumes via differencing before and after the co-registration step respectively done by our algorithm, and (f) change volume via the 3D EigenBlockCD-2 algorithm. Note that new periventricular high signal intensity focus is shown in green (short arrow) while the second unchanged area is not highlighted which indicate that it hasn’t change (long arrow).

The performance results of the initial co-registration step are shown in the first row of Figures 6-8. More specifically, in these figures, (a) show the reference slices of real T2-weighted MR volume of a brain taken in 2011, (b) show the corresponding test follow-up slices of the T2-weighted MR volume of the same patient taken in 2013, and (c) show the reference volume slices aligned to test volume slices after six affine transformations, three shifts and three rotations. The six parameters in this case are: 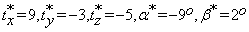and 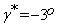More results of the co-registration are presented in Figures 1-3, Columns (a), (b) and (c) in Appendix A.

The detection step results are displayed in the second rows of Figures 6-8. More results of the detection step are shown in Columns (d) to (f) of Figures 1-3 in Appendix A.

We compared the change volume obtained by the 3D EigenBlockCD-2 algorithm with one obtained by simple differencing. First, simple differencing is performed between the original reference and test volumes, i.e., before the co-registration step. These results for slices # 2, 12, 14, and 19 are shown in Figures 6-8 (d) and for all 20 slices in Columns (d) of Figures 1-3 in Appendix A.Second, simple differencing is performed between the original test volume and the reference volume co-registered to the test volume by the 3D EigenBlockCD-2 co-registration step algorithm, i.e., after the initial alignment of the two volumes. These results for slices # 2, 12, 14, and 19 are shown in Figures 6-8 (e) and for all 20 slices in Columns (e) of Figures 1-3 in Appendix A.The results of the 3D EigenBlockCD-2 algorithm are shown in Figures 6, 7 and 8f, and for all 20 slices in Columns (f) of Figures 1-3 in Appendix A. As confirmed by the radiologist, these results show that our 3D EigenBlockCD-2 algorithm detect disease related and significant anatomical changes while rejecting changes due to patient position or other acquisition related artifacts which are clearly visible by the simple differencing method as shown in Figures 6, 7, 8d and 8e. For example, the new maxillary sinus mucosal thickening of the patient is detected and is shown in green in Figure 6f. Also in the follow-up scan, new small bilateral foci is detected which is shown in green in Figure 7f. In Figure 8f, our algorithm detects new periventricular high signal intensity focus shown in green as the short arrow points while the second unchanged area is not highlighted which indicate that it hasn’t change (as the long arrow points). All these clinical changes detected are confirmed by a radiologist.

The AEDL-2 and EigenBlockCD-2 algorithms are extended to process 3D MR images as obtained from MRI machine software. Initially, interpolation is used to generate extra slices between existing slices to include details and help co-registration process. We describe in detail both the co-registration and the change detection steps.

The co-registration step is formulated as a minimization problem where the cost function is defined as the L2 norm of the difference between one of the original volumes and the other volume transformed by an affine transformation. We use local dictionary techniques during the co-registration and the detection of changes steps, therefore, our algorithms does not require very accurate co-registration, as it can be seen from those images which are not perfectly aligned that we can still detect changes with great results. Results with real 3D volumetric data show that our co-registration step performs a reasonable alignment of the reference and the test MR volumes.

The change detection problem is defined as an optimization problem. We used the results from real data consisting of two 20-slice image volumes, shown in Appendix A, which visually demonstrates the performance of our algorithm. The average false positive rate and true positive rate that we calculated from these 20 slices are about 23.25% and 85.15%, respectively. From our results with real 3D MR images, we would like to note the following: a) in the last slide towards the top of head, the false positive rate of our algorithm is the worst compared to the other slices; but those false positives detected clearly include changes due to physiological changes in CSF; b) Significantly less false positives are present at the other levels of brain scan; c) in all cases, simple differencing produces many more false positive changes than our algorithm. The primary results with real 3D MR images demonstrate that the 3D EgienBlockCD-2 algorithm detects the significant clinical and physiology changes between consecutive MR scans while rejecting changes due to patient position and noise.

Next, we will collect more clinical data to conduct a more comprehensive performance statistical analysis and comparison. In future, we plan to explore the three dimensional dictionary techniques as another way for implementing change detection algorithms for MR volumetric data. We would like to investigate parallelizing implementation of the algorithms which we think is necessary for the 3D versions and for dealing with massive clinical image data. We also aim to make our algorithms practical and easy to use so that it can become a routine tool used by the radiologists.

The performance results of the 3D EigenBlockCD-2 algorithm with the completed set of 20 real MR volumetric slices are shown in Figures 1-3. More specifically, Columns (a) show the reference volume slices of real T2-weighted MR volume of a brain taken in 2011, Columns (b) show the corresponding test follow-up slices of the T2-weighted MR volume of the same patient taken in 2013, Columns (c) show the reference volume slices aligned to test volume slices after six affine transformations, Columns (d) (e) show the change volume slices via differencing before and after the co-registration step and finally Columns (f) show the change volume slices via the 3D EigenBlockCD-2 algorithm.