Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2013) Volume 6, Issue 11
Classifying Y-Short Tandem Repeat data has recently been introduced in supervised and unsupervised classifications. This study continues the efforts in classifying YSTR data based on four decision tree models: CHisquared Automatic Interaction Detection (CHAID), Classification and Regression Tree (CART), Quick, Unbiased, Efficient Statistical Tree (QUEST) and C5. A data mining tool, called IBM Statistical Package for the Science Social Modeler 15.0 (IBM® SPSS® Modeler 15) was used for evaluating the performances of the models over six Y-STR data. Overall results showed that the decision tree models were able to classify all six Y-STR data significantly. Among the four models, C5 is the most consistent modelm where it had produced the highest accuracy score of 91.85%, sensitivity score of 93.69% and specificity score of 96.32%.
Keywords: Classification, Supervised classification, Decision Tree, Predictive model, Y-STR data
Y Chromosome Short Tandem Repeats (Y-STR) is now a very popular method particularly used in Forensic Genetics, Genetic Genealogy and Genetic Anthropology. In Forensic Genetics, the method used for human identification applications, e.g. Paternity testing [1], Human migration pattern [2], rediscovering ancient cases [3], etc. In supporting the traditional genealogical studies, the Y-STR method has also been put in place as a new mechanism to trace family relatedness of Y-surname projects [4-6]. In a broader perspective, to establish groups of males, often called Haplogroups across the geographical areas throughout the world, the method has also been taken into account. As a result, a reputable reference, known as modal haplotype, used for defining groups of males all over the world, has been made available for public references (www.isogg.org). The modal haplotype is actually a haplotype diversity where the degree of relatedness has become spread out.
Efforts for automatically grouping Y-Short Tandem Repeat (Y-STR) data have been seen in recent publications. These efforts include supervised and unsupervised data mining approaches. For instances, Schlecht et al. [7] applied supervised data mining methods, e.g. Decision Tree, Bayesian model and Support Vector Machine in classifying haplogroup of Y-STR data [7]. For unsupervised data mining methods, a new clustering algorithm called k-Approximate Modal Haplotype (k-AMH) has specifically been introduced for clustering six Y-STR data [8]. The results produced by the k-AMH algorithm are very impressive, e.g. the algorithm obtained the highest mean accuracy score of 0.93 overall, compared to that of other clustering algorithms: k-Population (0.91), k-Modes-RVF (0.81), New Fuzzy k-Modes (0.80), k-Modes (0.76), k-Modes-Hybrid 1 (0.76), k-Modes-Hybrid 2 (0.75), Fuzzy k-Modes (0.74) and k-Modes-UAVM (0.70) [8]. Note that the two approaches above used the different Y-STR data. The former approach used the original DNA sequences based on 15 markers directly, while the later approach, utilized the number of repeats of the DNA fragment based on 25 markers subsequently, a similar method applied for the DNA testing results in genetic genealogy applications.
As the clustering methods have significantly shown impressive results, this study continues the effort to look into a supervised data mining approach by using the similar Y-STR data used by the clustering method above. This effort is important to benchmark the performance of supervised methods, such as the decision tree method for classifying the Y-STR data, particularly when involving mass grouping identifications. This is because the two approaches above mainly differ to each other. The supervised data mining approach uses labeled training data in obtaining the classifier, whereas the unsupervised data mining approach obtains the classifier automatically with unlabeled training data. For the supervised data mining approach, the main goal of classifying Y-STR data is to group Y-STR data in accordance with their target classes as the labeled training data. The target classes are based on the pre-defined Y-surname family groups or their haplogroups.
Several data mining tools, such as IBM® SPSS® Modeler, SAS® Enterprise Miner and IBM DB2® can be chosen for building predictive models for any data mining applications. As a consequence, this study is based on IBM® SPSS® Modeler 15 [9], which provides a package of building predictive models quickly and intuitively without the need for programming skills [9]. The use of SPSS Modeler (previously known as SPSS Clementine) for data mining applications has been reported in several publications, e.g. Yang et al. [10], Wah and Ibrahim [11], Kim [12], etc.
Y-STR data sets
The similar Y-STR data used previously in for a clustering application [8], were then used as benchmarking data sets for conducting experiments to evaluate the performance of the decision tree methods. Thus, six Y-STR data sets were set for the experiments and results analysis. The first, second and third data sets represented Y-STR data for haplogroup applications, whereas the fourth, fifth and sixth data sets represented Y-STR data for Y-surname applications. The main difference between the Haplogroup and Surname data set is the degree of genetics distance. The Haplogroup data are fairly distinct each other. Occasionally, the Y-STR haplogroup data may include subclasses that are sparse in their intra-classes. In contrast, the Surname data are composed of similar and very similar. Note that the degree of similarity is based on the mismatch results, when comparing the objects and their modal haplotypes. For example, many Y-STR surname objects are found to be similar (zero mismatches) and almost similar (1, 2, and 3 mismatches) in their intra-classes. Y-STR haplogroup data contain similar, almost similar and also quite distant objects.
All data sets were based on 25 markers. The markers included DYS393, DYS390, DYS394, DYS391, DYS385a, DYS385b, DYS426, DYS388, DYS439, DYS389I, DYS389II, DYS392, DYS458, DYS459a, DYS459b, DYS455, DYS454, DYS447, DYS437, DYS448, DYS449, DYS464a, DYS464b, DYS464c and DYS464d. The summary of each data set is as follows:
1) The first dataset consists of 751 objects of the Y-STR haplogroup belonging to the Ireland yDNA project [13]. The data contain only five classes (haplogroups), namely E (24), G (20), L (200), J (32) and R (475).
2) This dataset consists of 267 objects of the Y-STR haplogroup obtained from the Finland DNA Project [14]. The data are composed of only four classes (haplogroups): L (92), J (6), N (141), and R (28).
3) Consists of 263 objects obtained from the Y-haplogroup project [15]. The data contain three classes (haplogroups): Groups G (37), N (68) and T (158).
4) Consists of 236 objects combining four classes (Surnames groups) [16-19].
5) Consists of 112 objects belonging to the Philips DNA Project [20]. The data consist of eight classes (Surname groups): Group 2 (30), Group 4 (8), Group 5 (10), Group 8 (18), Group 10 (17), Group 16 (10), Group 17 (12) and Group 29 (7).
6) Consists of 112 objects belonging to the Brown Surname Project [21]. The data consist of 14 classes (surname groups): Group 2 (9), Group 10 (17), Group 15 (6), Group 18 (6), Group 20 (7), Group 23 (8), Group 26 (8), Group 28 (8), Group 34 (7), Group 44 (6), Group 35 (7), Group 46 (7), Group 49 (10) and Group 91 (6).
The values in parentheses indicate the number of objects belonging to that particular group. The detailed explanation on the data sets above, including the degree of similarity for each data set can be found [22].
Decision tree tool and algorithms
The experiments were conducted by using the IBM® SPSS® Modeler 15. Four decision tree models: CHi-squared Automatic Interaction Detection (CHAID), Classification and Regression Tree (CART), Quick, Unbiased, Efficient Statistical Tree (QUEST) and C5 provided by the IBM® SPSS® Modeler 15 were used for building the predictive model in classifying the six Y-STR data sets above. The overall process of building the predictive decision tree model pertaining to the analysis is shown in Figure 1. The model comprises of four nodes: Data Set node, Data Partition node, Predictive Model node and Assessment node. The Data Set node was used to associate for each Y-STR data set. The data set was then connected to the Data Partition node. A 70%: 30% training testing ratio was set for building a predictive model for each decision tree algorithm constructed by the Predictive Model node. The random seed in the partition node was set to 7654321. Finally, the performance of the models was evaluated through the Assessment node: the Analysis node and the Evaluation node. The accuracy of the models was obtained through the Analysis node, whereas the gain chart was generated through the Evaluation node. In order to compare all models in IBM® SPSS® Modeler 15, the Data Partition node was then connected to CHAID, CART, QUEST and C5 in serials. The performance of the predictive models was mainly based on accuracy, sensitivity and specificity scores. The accuracy score is as calculated using Eq. (1).
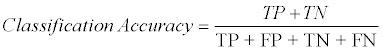 (1)
(1)
Where, TP is True Positive, TN is True Negative, FP is False Positive and FN is False Negative based on Confusion Matrix.
Furthermore, sensitivity and specificity scores were used for supporting the accuracy scores. The sensitivity and specificity methods are described in Eq. (2) and Eq. (3), respectively.
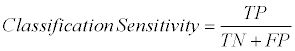 (2)
(2)
Where TP is True Positive, TN is True Negative and FP is False Positive based on Confusion Matrix.
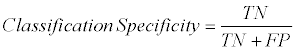 (3)
(3)
Where TN is True Negative and FP is False Positive based on Confusion Matrix.
The best model is mainly based on the highest testing/validation predictive accuracy scores. However, sensitivity and specificity scores are also used for further supporting the accuracy results. Table 1 shows the detailed predictive accuracy scores for each class and model. Overall results show that all models can be used for classifying the Y-STR data, particularly the Y-STR haplogroup data sets (Data sets 1-3). However, for Y-STR Surname data sets (Data sets 4 -6), the models faced a problem in classifying Data set 5 and 6. It seemed all models could not classify the data well. This problem was caused by the two characteristics of the Y-STR Surname data sets: the larger number of classes and the higher similarity of data. For examples, all models failed to classify Group 5 of Data set 5 because the objects in this group is very similar to each other. The similar problem also occurred to Group 20 of Data set 6. Note that the Y-STR Surname data are typically composed of the genetic distance, between 0 to 3.
| Accuracy (%) | |||||
|---|---|---|---|---|---|
| CHAID | CART | QUEST | C5 | ||
| Dataset 1 | Grp E | 87.5 | 75 | 37.5 | 87.5 |
| Grp G | 66.67 | 100 | 100 | 100 | |
| Grp L | 94.44 | 96.3 | 94.44 | 96.3 | |
| Grp J | 61.54 | 84.62 | 69.23 | 69.31 | |
| Grp R | 98.52 | 100 | 100 | 99.26 | |
| Average | 81.73 | 91.18 | 80.23 | 90.47 | |
| Dataset 2 | Grp L | 100 | 100 | 100 | 100 |
| Grp J | 100 | 100 | 100 | 100 | |
| Grp N | 100 | 100 | 100 | 100 | |
| Grp R | 87.5 | 87.5 | 87.5 | 87.5 | |
| Average | 96.88 | 96.88 | 96.88 | 96.88 | |
| Dataset 3 | Grp G | 100 | 100 | 100 | 100 |
| Grp N | 100 | 100 | 100 | 100 | |
| Grp T | 97.83 | 97.83 | 97.83 | 97.83 | |
| Average | 99.28 | 99.28 | 99.28 | 99.28 | |
| Dataset 4 | Grp D | 100 | 100 | 100 | 100 |
| Grp F | 100 | 100 | 100 | 100 | |
| Grp M | 100 | 100 | 100 | 100 | |
| Grp W | 83.33 | 100 | 100 | 100 | |
| Average | 95.83 | 100 | 100 | 100 | |
| Dataset 5 | Grp 2 | 100 | 90 | 100 | 90 |
| Grp 4 | 100 | 100 | 100 | 100 | |
| Grp 5 | 0 | 0 | 0 | 0 | |
| Grp 8 | 100 | 100 | 100 | 100 | |
| Grp 10 | 100 | 100 | 100 | 100 | |
| Grp 16 | 0 | 0 | 100 | 100 | |
| Grp 17 | 100 | 100 | 100 | 100 | |
| Grp 29 | 100 | 0 | 100 | 100 | |
| Average | 75 | 61.25 | 87.5 | 86.25 | |
| Dataset 6 | Grp 2 | 100 | 100 | 100 | 100 |
| Grp 10 | 100 | 85.71 | 71.43 | 100 | |
| Grp 15 | 0 | 0 | 0 | 100 | |
| Grp 18 | 100 | 0 | 0 | 100 | |
| Grp 20 | 0 | 0 | 0 | 0 | |
| Grp 23 | 100 | 100 | 100 | 100 | |
| Grp 26 | 100 | 75 | 100 | 100 | |
| Grp 28 | 100 | 0 | 50 | 100 | |
| Grp 34 | 100 | 0 | 100 | 50 | |
| Grp 35 | 100 | 100 | 100 | 100 | |
| Grp 44 | 100 | 0 | 0 | 100 | |
| Grp 46 | 0 | 100 | 0 | 100 | |
| Grp 49 | 100 | 0 | 0 | 100 | |
| Grp 91 | 100 | 100 | 100 | 100 | |
| Average | 78.57 | 47.19 | 51.53 | 89.29 | |
| Overall | 83.13 | 69.48 | 79.68 | 91.85 | |
Table 1: Classification of accuracy scores for testing sample.
However, in overall performance, C5 model produced the highest predictive accuracy scores. The model recorded an impressive of accuracy score of 91.85, compared of that to the other models: CHAID (83.13), CART (69.48) and QUEST (79.68). Observably, the accuracy score obtained by C5 model for Data set 6 was the main contribution of its overall performance. The model obtained the highest accuracy score of 89.29, in which outperformed the other models: CHAID (78.57), CART (47.19) and QUEST (51.53). This is due to some advantages of the C5 model e.g. splitting criteria and pruning method. A multi-way splitting tree has given an advantage to C5 model when dealing with a larger number of clusters. In fact, another multi-way splitting model, CHAID also produced an impressive accuracy score of 78.57. Note that the other models, CART and QUEST are based on binary tree splitting criteria. On top of that, the C5 model with its pruning method using Binomial Confidence Limit seems to be a good method to classify the data with very similar characteristics, such as Y-STR Surname data.
As for sensitivity (Table 2) and specificity (Table 3) results, the average sensitivity and specificity scores, CART was rated the least with 81.62% for sensitivity score and 86.13% for specificity score. On the other hand, C5 once again surpass the other models by having highest sensitivity and specificity scores with 93.69% and 96.32%, respectively.
| CHAID | CART | QUEST | C5 | |
|---|---|---|---|---|
| Data set 1 | 81.73 | 91.18 | 80.23 | 90.46 |
| Data set 2 | 96.88 | 96.88 | 96.88 | 96.88 |
| Data set 3 | 99.28 | 93.22 | 99.28 | 99.28 |
| Data set 4 | 95.83 | 100.00 | 100.00 | 100.00 |
| Data set 5 | 75 | 61.25 | 87.5 | 86.25 |
| Data set 6 | 78.57 | 47.19 | 55.10 | 89.29 |
| Average | 87.88 | 81.62 | 86.50 | 93.69 |
Table 2: Classification of sensitivity scores for testing sample.
| CHAID | CART | QUEST | C5 | |
|---|---|---|---|---|
| Data set 1 | 98.22 | 99.06 | 99.52 | 99.19 |
| Data set 2 | 99.65 | 99.22 | 100.00 | 99.22 |
| Data set 3 | 99.42 | 97.53 | 99.44 | 99.44 |
| Data set 4 | 99.53 | 100.00 | 100.00 | 100.00 |
| Data set 5 | 75 | 73.56 | 87.5 | 87.5 |
| Data set 6 | 77.74 | 47.38 | 54.32 | 92.58 |
| Average | 91.59 | 86.13 | 90.13 | 96.32 |
Table 3: Classification of specificity scores for testing sample.
Based on accuracy, sensitivity and specificity scores, C5 is significantly the best model for classifying Y-STR data. For further verification, Figures 2a-2f show the predictive performance comparisons of the four models using the gain chart. The Gain chart is a useful way of visualizing how good a predictive model is. It shows that C5 model is consistent throughout all data sets. Thus, C5 is a good model of classifying Y-STR data when its gains chart rose steeply toward 100% and then level off, particularly for data set 2 (Figure 2b), data set 4 (Figure 2d), data set 5 (Figure 2e) and data set 6 (Figure 2f). For data set 1 and 3, the gain for C5 is slightly competitive to the other models.
Based on the experiments above, the decision tree methods are very significant techniques in classifying Y-STR data. Overall results show that the methods can be used for grouping Y-STR data, even though dealing with a uniqueness of Y-STR data. However, among the four models, C5 model has significantly shown its better performance in classifying the Y-STR data. Through its classification accuracy scores, supported by its sensitivity and specificity scores, the model has obviously proven as the best model in classifying Y-STR data. Looking at the gain chart, C5 model has risen steeply toward 100% before levelling off.
This research was supported by Fundamental Research Grant Scheme, Ministry of Higher Education Malaysia. We would like to thank RMI, UiTM for their support for this research. We extend our gratitude to many contributors toward the completion of this paper, including Associate Prof. Dr. Yap Bee Wah for introducing us SPSS Modeller.