Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Review Article - (2014) Volume 4, Issue 6
In this review, a detailed discussion on salient features of intermolecular interactions leading to phase separation and coacervation is discussed. Biomolecular solutions exist as gels, coacervates and melts with each of these phases having its signature physico-chemical properties which is discussed in this review. The discussions are supported by robust experimental data obtained from an array of methods like turbidimetry, electrophoresis, viscosity, light scattering etc. The inevitability of the phenomenon of self-organization in biopolymers results in generation of a variety of soft matter phases which do not, however, make it predictable. For instance the associate aggregation is a process which remains obscure, as every protein aggregates in a different manner under different conditions. One known feature to the aggregation of proteins is the strong dependence upon pH, salt concentration, and temperature. Beyond the influence of these factors and their effects on aggregation, the process is not well understood. In summary, a comprehensive account of biomolecular phase states and their inherent attributes are presented in this review.
Potential applications of coacervates are many starting from protein purification, drug encapsulation to treatment of organic plumes. This calls for better understanding of the coacervate structure and the transport of biomolecules inside this phase. Several questions pertaining to the structure of coacervates can arise. The foremost of these is, is it a gel-like or a solution-like phase? Though presence of hydrogen bonding and hydrophobic sites on the polyions influence biomolecular binding, they hardly play any role in deciding the persistence length of the polyion unlike the surface charge. Interestingly, we observed that the differential binding (SPB versus EB) was found to be a function of intrinsic persistence length only which we conclude as a significant observation.
Keywords: Coacervation; Persistence length; Solvent polarity; Polyelectrolyte charge; Ionic strength; Surface patch binding; Viscoelastic behavior and internal structure
Coacervation: Coacervation is a thermodynamic transition which allows a homogeneous solution of charged macroions to undergo liquidliquid phase separation, giving rise to a polymer- rich dense phase coexisting with its supernatant. These two liquid phases are immiscible but are thermodynamically compatible. The polymer-rich dense phase is often called the coacervate. Structurally it lies between the crystalline and liquid phases. Thus, it can bear intermediate range structural order and can be referred to as a mesophase. Coacervation has been mostly studied in aqueous solutions of charged synthetic or biological macromolecules in the past. In particular, protein-polysaccharide and protein-protein coacervates have attracted much attention because of their inherent potential in generating new biomaterials. In addition, such studies provide basic understanding of specific and non-specific interactions operating between complementary polyelectrolytes [1-6] or polyelectrolyte-polyampholyte [7-15] pairs. Normally, polysaccharides are strong polyelectrolytes whereas proteins, in addition, can be polyampholytes. Hence, the association problem reduces to that of the general study of interaction between polyelectrolyte (PE) and polyampholyte (PA) molecules [6,16]. A recent review encapsulates many of the anomalous as well as the salient features of protein-polyelectrolyte interactions [1] The phenomenon of protein based coacervates, formed of strong electrostatic interactions, has been reported for β-lactoglobulin- gum Arabic [7,8], whey proteingum Arabic [9,10], gelatin-chitosan [11], gelatin-agar [12,13], gelatingelatin [14], gelatin- DNA [15] and β-lactoglobulin-pectin systems [17]. The diversity of material properties associated with coacervates can be gauged from the fact that β-lactoglobulin-gum arabic coacervates were found to be associated with vescicular to sponge-like internal structure whereas whey protein-gum arabic coacervate was observed to be a highly concentrated (melt-like) phase. In contrast, β-lactoglobulin-pectin coacervates were found to be a heterogeneous phase comprising of pectin networks with protein domains forming the junction points [17]. It has been shown that a polyelectrolyte, DNA and a polyampholyte, gelatin can undergo associative interaction and form complex coacervates with interesting thermal properties [15]. Further, it has been realized that in a class of systems coacervation transition is governed by surface selective patch binding even though both the polyions carry similar net charge [11,18,19]. In particular, in SPB interactions complementary polyions (normally a PA-PE pair) seek oppositely charged patches to bind overcoming the repulsion occurring between similarly charged surface patches. This is often referred to as binding on the wrong side of pH.
The following provides a brief structural introduction to various biomolecules used in the present review. As per Merck index, Gelatin, a polyampholyte obtained from denatured collagen, is a polypeptide with the chemical composition of this biopolymer given as follows: Glycine constitutes 26%, alanine and arginine are in 1:1 ratio together constitute ≈20%, proline is ≈14%, glutamic acid and hydroxyproline are in 1:1 ratio constituting ≈22%, aspartic acid ≈6%, lysine ≈5%, valine, leucine and serine constitute ≈2.0% each, rest 1% is comprised of isoleucine and threonine etc. Depending on the process of recovery the gelatin molecules bear different physical characteristics. Type-A gelatin is acid processed, has an isoelectric pH, pI ≈9 whereas the alkali processed type-B gelatin has pI≈5.
Chitosan (poly [β-(1-4)-2-amino-2-deoxy-D-glucopyranose]) is a biodegradable cationic polysaccharide produced by partial deacetylation of chitin derived from naturally occurring crustacean shells. The polymer is comprised of copolymers of glucosamine and N-acetyl glucosamine. Chitosan has an apparent pKa value between 5.5 and 6.5 and upon dissolution in acid media the amino groups of the polymer are protonated rendering the molecule positively charged. At neutral and alkaline pH, most chitosan molecules lose their charge and precipitate from solution [20].
The biopolymer, Agar comprises mainly of alternating β-(1-4)-D and α-(1-4)-L linked galactose residues in a way that most of α-(1-4) residues are modified by the presence of a 3,6 anhydro bridge [21]. Other modifications commonly observed are mainly substitutes of sulphate, pyruvate, urinate or methoxyl groups. The gelation temperature of agar is primarily decided by the methoxy content of the material. Agar sols form thermo-reversible physical gels with the constituent unit being anti-symmetric double helices [22,23].
Calf thymus DNA (nominal Mw=50-100 KDa) was obtained from Acros Organics. This preparation was a mixture of ss and ds DNA. Agarose gel electrophoresis was performed using the standard description. For plasmid DNA samples, 1% agarose was prepared in 1X TAE [40 mM Tris-Acetate, 1.0 mM EDTA (pH 8.0)] buffer by heating, cooled to 45°C and ethidium bromide (0.5 μg/ml) was added to stain the gel. DNA samples were mixed with one-sixth volume of DNA gel loading buffer and loaded onto the wells. Electrophoresis was performed at 5 V/cm in TAE buffer (40 mM Tris-Acetate, 1.0 mM EDTA, pH 8.0) and DNA samples were visualized, on an UV transilluminator at 302 nm. The number of base pairs estimated was 200 for our sample (Tables 1 and 2).
| S. No. | Biopolymer | Nature | pI | Rh (nm) | Rg (nm) | lp (nm) |
|---|---|---|---|---|---|---|
| 1. | DNA | polyanion | -- | 140±10 | 117±10 | 50[24] |
| 2. | BSA | polyampholyte | 4.6 | 3.5±0.5 | 3.1±0.5 | 7 |
| 3. | Chitosan | polycation | -- | 340±40 | 260±40 | 17[25] |
| 4. | Gelatin -A | polyampholyte | 9.0 | 58±3 | 55±3 | 10[26] |
| 5. | Gelatin -B | polyampholyte | 4.9 | 23±2 | 34±2 | 2[27,28] |
Table 1: Listing of physical properties of biopolymers used in this work. Apparent hydrodynamic radius Rh, radius of gyration Rg, intrinsic persistence length lp and pI values are presented. Rh, Rg and pI values were measured. [95] - Reproduced by permission of the PCCP Owner Societies.
| System | Interaction at | Overcharge Zeta potential/ mV | ||
|---|---|---|---|---|
| pHc | pHΦ | Water | IL solution | |
| DNA-GB | Surface patch | Electrostatic | +12.0 | +2.4 |
| DNA-BSA | Surface patch | Electrostatic | +13.5 | +3.0 |
| DNA-GA | Electrostatic | Electrostatic | +15.0 | +4.5 |
| DNA-Chitosan | Electrostatic | Electrostatic | +28.0 | +9.0 |
Table 2: Comparison of interaction type and overcharged potential of Complex coacervates of DNA with different polyions with and without IL. [95] - Reproduced by permission of the PCCP Owner Societies.
Liquid-Liquid phase transition
In a polyelectrolyte solution, the phase transition is driven by electrostatic solute-solvent interaction which results in gain in the configurational entropy and the formation of amorphous randomly mixed polymer-rich phase remaining in equilibrium with dilute supernatant. Physical conditions for phase separation are deduced explicitly when the complexation between oppositely charged polyelectrolytes leads to self-charge neutralization [24-28].
Figure 1 depicts two pictures, one representing a coacervating solution and other showing a solution undergoing precipitation.
As far as thermodynamics of liquid-liquid phase transition leading to coacervation is concerned, not everything is known. Phase separation models proposed in the literature do not possess all the possible interactions adequately. However, there is unanimity in the following description:
That a homogenous solution containing N1 molecules of solvent and N2 molecules of solute at temperature T and pressure P, will remain stable as long as the free energy of the solute F2 in solution obeys the thermodynamic condition
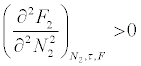
That the phase separation of the coacervate phase from the dilute supernatant is a dehydration (of the individual polyion) process
That charge neutralization of polyion segments precedes phase separation
That the polyions do not precipitate out of the solvent because of entropy gain achieved by random mixing of polyions in the coacervate phase.
In the summary, coacervation proceeds in two steps, first, the selective charge neutralization of polyions dictated by electrostatic interactions, and second, the gain in entropy achieved by random mixing of polyions in the dense phase plus the gain in entropy due to release of counter-ions to the solvent.
From the point of thermodynamics, change in molar heat capacity ΔCp associated with intermolecular complexation dictates the possibility of binding between asymmetrically charged polyelectrolytes. Recent literature [29] reveals that complex formation between weakly charged polyelectrolytes is driven by the negative enthalpy ΔH due to electrostatic attraction, with counter ion release entropy playing only a minor role. On the other hand, the complex formation between highly charged polyelectrolyte (like in DNA) is driven by large counter ion release entropy and opposed by a positive enthalpy change. A large variation of counter ion release entropy as function of salt concentration was only detected for highly charged polyelectrolytes. The molar heat capacity Cp of the system plays a vital role in variation of binding enthalpy with the temperature. This originates from the changes in degree of surface hydration in the free and complex molecules. If ΔCp has large positive values, the system leads to charge neutralization via ionization process (protein-polysaccharide systems), if ΔCp is negative, the system provokes hydrophobic interactions and if ΔCp is positive with negative ΔH at all temperatures, there is significant contribution of H-bonding [30]. In a recent study of gelatin-agar system done in our laboratory [12], no temperature effect was observed either on the critical pH of complex formation or on the pH where phase separation occurred. The phase separation was not promoted by electrostatic interactions, hydrogen bonding or hydrophobic interactions but through polarization induced attractive interactions. Main reason for such a complex formation was the existence of small “patches” on the protein, i.e. localized regions with higher charge density. Here the ion-dipole interaction overcomes ion-ion repulsion or if the polyacid/polybase is strong enough or the protein has a high enough regulation capacity a reversal of charge may be induced on the protein. In our case, the high charge density polyelectrolyte DNA was found to undergo associative interaction with GB and BSA, both polyampholyte molecules with heterogeneous charge distribution, following the aforesaid surface patch binding protocol. Table 2 provides a summary of all the salient features that was observed in our studies.
Simple coacervation
Gelatin is a polypeptide, and is a degraded product of native collagen. The degradation is performed either through acid or base treatment protocol. This generates two types of gelatin, A and B.
Gelatin B is a random coil polymer carrying positive and negative charge sites in almost 1:1 ratio. At the same time, it is associated with small persistence length ≈2 nm. The zeta potential curves shown in Figure 2 imply an isoelectric pH≈5, though small concentration dependence in its value could be clearly seen. Specifically, a gelatin solution prepared close to pH=5 is required to be turned into a poor solvent for gelatin molecules which will ensure chain collapse facilitating intermolecular electrostatic interaction leading to charge neutralization, and finally, coacervation. This is achieved by adding ethanol (a non-solvent) to gelatin solution.
Figure 3 implies that as coacervation point is reached, the zeta potential of the aggregates that are formed due to associative interactions tends to a very low value indicating effective charge neutralization achieved due to strong electrostatic binding between oppositely charged segments of the polymer. In fact, occurrence of turbidity maxima coincides with minimum zeta potential which is in complete agreement with the requirement dictated by models of phase transition [11]. The experimental data indicate the interplay of at least two different types of interactions that precede coacervation:
(i) Hydrophobic interactions between hydrophobic patch of gelatin molecule with aliphatic hydrocarbon tail of alcohols and,
(ii) Solute-solvent interactions.
It should also be realized that when two opposite charged segments join together, some amount of counter-ion is always released into the solvent, thereby increasing the entropy of the solution. This can also assist the process to move towards coacervation [30].
In complex coacervation, a pair of complementary polyelectrolytes or a polyelectrolyte-colloid undergoes associative interaction, charge neutralization followed by liquid-liquid phase separation. The screened Columbic interaction is primarily responsible for causing intermolecular binding through associative forces. Therefore, following property of the solvent medium and polyelectrolyte is important: (i) polyelectrolyte flexibility (persistence length), (ii) solvent polarity, (iii) polyelectrolyte charged state, (iv) ionic strength, and (v) surface patch binding. We shall be discussing these issues in the following sections.
Effect of persistence length
Apart from surface charge density, the chain flexibility of polyions plays an important role in complex formation between complementary polyelectrolytes or polyelectrolyte-polyampholyte pairs. Seyrek et al. [31] have shown that the binding constant in the system of -lactoglobulin-poly(vinylsulfate) was inversely related to persistence length of poly(vinylsulfate) chain implying that protein binding was enhanced by the flexibility of polyanion particularly in the case where protein charge was negative. Past results [32] have categorically established that one should use either the intrinsic persistence length l0 or some intermediate value between that and the total persistence length lp while discussing polyion flexibility. In the Odijk-Skolnick- Fixman formalism [33], lp is a sum of l0 and electrostatic persistence length le is given by:
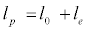 (1)
(1)
The parameter le depends on the intramolecular Coulombic forces and to a very good approximation is given by 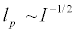 , where I is the ionic strength of the solution. Chain flexibility is associated with persistence length through the Kratky-Porod description of polymers [34,35]. According to this model, the polymer chain is composed of segments of length lk, where lk is the Kuhn segment length and
, where I is the ionic strength of the solution. Chain flexibility is associated with persistence length through the Kratky-Porod description of polymers [34,35]. According to this model, the polymer chain is composed of segments of length lk, where lk is the Kuhn segment length and 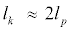
However, it is unclear if the effect of persistence length on overcharging of DNA-polyion intermolecular complexes and binding phase diagrams are ubiquitous. Herein, we examine the effect of persistence length on DNA-polyion binding and complex formation in a series of controlled experiments. In order to cover one decade spread in the persistence length, we have chosen three common proteins: gelatin B (lp =2 nm), bovine serum albumin (lp =7 nm) and gelatin A (lp =10 nm), and a polysaccharide, chitosan, (lp =17 nm) as binding partners to DNA (lp =50 nm). The intermolecular complex formation was exhaustively investigated in water and in IL solutions using turbidity, dynamic light scattering and electrophoresis techniques. The physical attributes of the biopolymers used in the current studies are listed in Table 1. Note that BSA has a compact geometry with hydrodynamic radius Rh= 3.5 nm. For such a molecular structure the effective persistence length will be lp≈ 2Rh= 7 nm. In this report, we shall refer to gelatin A and B, BSA and chitosan as polyions. The pH-dependent electrophoretic profiles of the biopolymers clearly establishes strong polyanionic behaviour of DNA, weak polycationic nature of chitosan and clear polyampholyte attributes of gelatin A and B, and BSA molecules.
Solvent polarity
The best way to alter the solvent polarity is through addition of ionic liquids to the aqueous medium. In ionic liquids (IL) solutions one introduces mobile ions, hydrophobicity and hydrogen bonding possibility simultaneously into the continuous phase. These liquids, comprising of inorganic anions and organic cations, are associated with negligible vapour pressure, high thermal, chemical and electrochemical stability that enable these to be treated as green solvents [36,37]. Due to their characteristic hydrophobic-hydrophilic balance, ILs are widely used as surface active agents to study micellization behaviour in water [38-42]. In addition, this particular attribute makes these liquids compatible with many common solvents thereby generating designer solvents with controlled hydrophobicity, polarity and miscibility. This property of IL has considerable bearing on molecular biophysics of proteins and polypeptides. Ionic liquids and their solutions are being used as biocatalytic reaction media, biosensors, protein and enzyme stabilizers etc. [41,42]. Numerous studies have explored protein and enzyme stability in these solvents that conclude that the observed catalytic activity of enzymes was due to the heterogeneously dispersed state of enzymes [43-46]. In our previous work [47], we have categorically shown the efficacy of various imidazolium based ionic liquids in stabilizing protein dispersions.
Polyelectrolyte charge
The electrophoretic behaviour of agar and gelatin molecules as well as their intermolecular complexes was studied at room temperature. In order to understand the mechanism of formation of the Ag-Ge complex, the zeta-potential of 0.01% (w/v) agar and 0.01% (w/v) gelatin-B solutions were measured separately at different pH. Measurement on agar-gelatin intermolecular complexes at different pH was also carried out after dilution of the samples by 10 times. Since the net surface charge of the system is not much affected by its dilution, the data can be assumed to be comparable to the original system. No reliable measurements could be performed on samples prepared with salt. The representative data is shown in Figures 4 and 5. The results reveal that the pI of gelatin was close to 6 and agar was a polyanionic molecule with zeta potential ≈-20 mV. Beyond pH =6, gelatin molecules were weakly charged with a small negative zeta potential ≈-5 mV. The titration profile shown in Figure 5 implies that first appearance of turbidity was noticed at pHC=7.4. This refers to the formation of intermolecular soluble aggregates. Thus, the two polyions could form aggregates when the net charge on both was negative. The turbidity continued to rise and a peak was observed at pH≈6 and even at this pH, both the biopolymers continued to carry similar charge. The soluble aggregates precipitated out of the interacting solution at pHprep4.5. This is the point of maximum interaction and a stage for rapid formation of coacervates.
Figure 5: The plot shows the variation of pHc, pHΦ and pHprep as function of NaCl concentration. Note that pHc and pHΦ are invariant of NaCl concentration while and pHprep shows a decreasing trend with increase in NaCl concentration. Solid lines are guide to the eye. Reproduced with permission from American Chemical Society [Boral et.al 2010].
The issue of charge reversal and overcharging of DNA-colloid complexes was examined by Nguyen and Shklovskii [46] and they made the following conclusions: (i) at low colloid concentration, the DNA-colloid complexes are negatively charged with DNA wrapping the colloids while (ii) at high colloid concentration the complexes showed charge reversal and revealed positive charge. The aforesaid two situations are separated by an intermediate phase where the complexes are fully charge neutralized; here DNA-colloid condensates exist. Thus, the concentration of colloidal macroions governed the condensation and re-entrant condensation in this system. In a further extension of their work, the same group [47] studied the phase diagram of DNA and polycation (PC) and observed that complex charge state was decided by DNA: PC charge ratio. In this study existence of overcharged intermolecular complexes were clearly proposed. Gurovitch et al. and others [48-50] proposed an idealized model for the adsorption of weakly charged polyelectrolyte onto oppositely charged colloidal particles.
Ionic strength
Turbidity measurements were performed on gelatin B-agar solutions prepared with mixing ratio =1:1 and NaCl concentrations of 0 M, 0.01 M, 0.05 M and 0.1 M at various pHs ranging from 10 to 4 (Figure 4). Figure 5 shows clearly how various transition pHs vary with NaCl concentration. At pHc (= 7.4) there is slight turbidity showing the initiation of intermolecular binding between gelatin and agar chains forming soluble aggregates. Here both agar and gelatin molecules are negatively charged, since pHc > pI of gelatin-B (pI≈6) (Figure 4). But gelatin, being a polyampholyte, still has some positively charged patches on its surface to promote surface selective binding at these locations. One could observe no change in pHc with change in NaCl concentration (Figure 5) suggesting no significant role played by the mobile ions in screening the interactions and affecting the binding. At pHΦ (near pI of gelatin) the gelatin molecules have a minor net positive charge on its surface, and hence the coacervation process is enhanced showing rapid charge neutralization and significant increase in turbidity. With further lowering of pH, similar trend was observed until the soluble aggregates precipitated out at pHprep (=5±0.2, see Figures 4 and 5). Salt screening effect is clearly not seen from the data presented in the Figure 5, where pHC and pHΦ values remained invariant of the ionic strength which is a characteristic signature of surface patch binding phenomenon. This indicated that the intermolecular interactions were poorly screened by mobile ions. The ability of the system to undergo coacervation transition in absence of salt implies that the two biomolecules followed a symmetric binding character as far as the stoichiometry was concerned. There was a notable change in pHprep from pH 5 to 4.2 which was observed on increasing salt concentration. This depicts that the mobile ions stabilize the system on pH change.
Normally, for pH > pHΦ, one observes the formation of large insoluble complexes that undergo precipitation immediately, which is observed in turbidity-pH profile data as a sharp drop in measured turbidity values [49,50]. In the present case, it was observed that for pH > pHΦ the turbid solution did not undergo precipitation instantaneously, and we found a flat or saturated type of curve (Figure 5) extending beyond the maximum turbidity pH, but the precipitation occurred within 15 minutes. This can be explained in the following way. Initially the size of the insoluble aggregates was small which was not conducive for instantaneous precipitation. These aggregates grew to a larger size with time following Ostwald ripening and eventually precipitation ensued. These insoluble aggregates were not amenable to electrophoresis measurements because these dispersions sedimented gradually. At pHΦ, a binding saturation was reached that was dictated by the stoichiometry of the polymers involved.
The formation of coacervates versus aggregates could be related to the stiffness and to the charge density of polysaccharides, more rigid ones leading to aggregates and flexible ones to coacervates. Agar is well known for its rigid rod shaped fiber bundles which is stiff enough due to its high charge density [51] whereas gelatin is known to bear a persistence length of 2 nm showing its flexible nature [27]. The phase separation could be visualized as a spinodal decomposition [52] or nucleation and growth [53] mechanism. However, it appears that all the systems have their signature interaction mechanisms. For instance, the coacervation behavior of some polymers such as elastin [54] appears to be an example of mixed coacervation intermediate between the classes of uni-complex and simple coacervation as defined by Bungenberg de Jong [6]. Again in some literature, we find that complex coacervates are highly unstable and sometimes a toxic chemical agent such as gluteraldehyde is added to stabilize the material [54]. Several theoretical models have been proposed to address the phase separation kinetics that leads to coacervation transition. Some of these are: Voorn-Overbeek [55], Veis-Aranyi [56,57], Nakajima- Sato [58], Tainaka [59] and Amarnath-Bohidar [60] models. The salient features of all the models are discussed in ref. [61]. Coacervates are believed to have a weakly interconnected network system associated with strong concentration fluctuations that prevail over many length and time scales which allows these systems to evolve dynamically with time [61].
Surface patch binding
In a small class of systems liquid-liquid phase separation gets initiated by surface selective patch binding [11,18,19] even though both the polyions carry similar net charge. This is often referred to as binding on the wrong side of pH. In the present work, we have shown that the formation of intermolecular soluble complexes and the phenomenon of coacervation could be achieved when a polyelectrolyte (agar) interacts with a polyampholyte (gelatin) through surface selective patch binding. Little is known about the affect of ionic strength on such binding mechanisms which is the main focus of this work. In order to get a better feeling of the system, the results are compared with the salient features reported in gelatin simple coacervates [25,62], and gelatin A-gelatin B [14], gelatin-chitosan [11] and gelatin A-agar [63] complex coacervates. The surface selective binding process has been explained through potential energy calculations following a simple model. In this article the terms complexes and aggregates are being used interchangeably.
The phenomenology of formation of intermolecular complexes leading to phase separation depends on the physical environment of the system. Thus the pH, polymer charge density, ionic strength, temperature and mixing ratio, all play a vital role in the formation of the complexes. The intermolecular complex formation is an associative interaction involving the attractive forces and entropy of the system. Thus, it is imperative to begin such studies with the electrophoretic characterization of the samples.
Unlike electrostatic interactions, surface patch binding phenomena is poorly understood which makes it imperative to discuss it in some details in the context of DNA-GB and DNA-BSA systems. Such bindings are often referred to as binding on the wrong side of pH which has been reported in a variety of systems [18,19,64]. Surface patch controlled attractive electrostatic interactions between proteins and adsorbent having same net charge was studied, by ion-exchange chromatography (IEC), for lysozyme, ribonuclease-A, cytochrome-c and α-chymotrypsinogen systems and it was observed that such interactions were governed by the characteristics of the solvent medium like, the pH, ionic strength etc. [64]. The “retention maps” for the pH dependences of IEC capacity factors were quite revealing as this established the existence of patch binding without doubt. This was attributed to the heterogeneous charge distribution on the protein surface that facilitated binding though the net charge on protein may be of the same kind as that of the absorbent [65,66].
In a more detailed and quantitative experiment the intermolecular binding between the selected proteins RNAse, lysozyme and BSA, and polyelectrolytes with varying linear charge densities was studied by DLS and turbidimetry [18,19]. These results supported the conclusions of “retention maps” constructed and reported by Regnier et al. [67]. It was also shown that the persistence length of the polyelectrolyte played a very important role in the binding process. Namely, higher the flexibility greater is the extent of binding. An approximate model for quantitative estimation of charge on the soluble complexes, both at pHC and pHΦ , was proposed which did imply charge neutralization due to surface patch binding. The qualitative features observed by Regnier et al. [67], Gao et al. [19] and Park et al. [18] are clearly visible in the intermolecular complexation data presented here. These can be summarized as follows: (i) formation of intermolecular soluble complexes were observed with both biopolymers having same kind of net charge, (ii) soluble complex is, actually, the partially charge neutralized DNA and (iii) the interaction is electrostatic and is site specific. In addition, we noticed significant overcharging of DNApolyion complexes not reported hitherto.
Agar is polyanionic bioploymer that exhibits strong polyelectrolytic character in the entire range of pH. But pI of gelatin is 6 which means pH < pI it behaves as a polycationic molecule and pH > pI, it shows polyanionic characteristics. The intermolecular binding for all four samples was initiated near pHC = 7.2 as observed from the turbidity experiments (Figure 4). However, we also observed significant increase in turbidity at pHC < pH < pHΦ. In this range the gelatin molecule acquires small positive charge on its surface although the overall charge still remains negative [66]. Again when we consider the stiffness of the polymer chains, agar having all negative charges on it, is stiffer than the gelatin molecule which has both positive and negative charges over it. The agar molecule cleverly selects those patches on the gelatin molecule that are positively charged and binds to it selectively to yield intermolecular complexes. This mechanism is well known as surface selective patch binding and is elaborately explained earlier [11,67-69]. This mechanism is also supported by the electrophoretic data given in Figure 4. Zeta potential data of complexes indicate that there is an intermolecular charge neutralization mechanism involved that resulted in producing these complexes bearing intermediate charge.
A simple model calculation has been performed in order to show the importance of electrostatic potential energy in surface selective binding mechanisms. The electrostatic charges on the agar and gelatin particles are determined separately from the Smoluchowski approximation using zeta potential data [70]
Q = (3/2).ε.Rh.Z (2)
Where ε is the permeability of the medium, Rh is the hydrodynamic radius of the particle and Z is the zeta potential of the particle. A representative estimation of electrostatic interaction energy can be carried out in the pH window 4 to 9 where most of the kinetics is located. The apparent hydrodynamic radius Rh of gelatin is 50 nm [30,62] and that of agar is 100 nm (measured). The intermolecular distance can be determined from concentration and molecular weight as
Number density of agar in the solution NAg = (NA/100).CAg/MAg (3)
Number density of gelatin in the solution NGe = (NA/100).CGe/MGe (4)
where CAg and CGe are concentrations of agar and gelatin in the system, MAg and MGe are molecular masses of agar and gelatin molecules respectively and NA is the Avogadro’s number
Intermolecular distance in the system ds=(1/(NAg+NGe))1/3 (5)
The intermolecular distance ds was estimated to be ≈ 63 nm in this particular system. Gelatin is a polyampholyte bearing 13 % of residues that are acidic and 15 % residues are basic in nature (Merck Index data). Assuming that all the acidic residues are de-protonated and all basic residues are protonated at pHC ≈7, the chain has a surplus of 2% positively charged patches that electrostatically bind to agar molecule. Since, the intermolecular separation and charge on agar and gelatin are known; it is possible to estimate the potential energy of interaction between the two biopolymers given by
Potential Energy ≈ (1/4πε) (QGeQAg/ds) (6)
Where the excess charge on gelatin is QGe and charge on agar molecule is QAg. The potential energy is plotted as function of pH in Figure 6 and for convenience it is plotted in arbitrary units for comparison with titration profile data. The zeta potential of intermolecular complexes is also plotted in the same graph. The potential energy plot is quite revealing. There is strong attraction between the agar and gelatin chains as one goes for pH<6. The pHC is clearly discernible in the plot where potential energy shows reduction and intermolecular complexes have a zeta potential ≈ -20 mV. At the maximum turbidity point (pHΦ) a sharp drop in potential energy is noticed that corresponds to strong intermolecular binding maximum and rapid coacervation. The midpoint between pHΦ and pHprep is located at pH ≈5.4 where the intermolecular complexes achieve complete charge neutralization (zero zeta potential). At this pH, the potential energy changes its slope again allowing coacervation to proceed aggressively. For pH> 7.5, there is strong intermolecular repulsion, which can be noticed as a sharp rise in the potential energy curve. Complex formation and coacervation was observed in the pH range where the two biopolymers had the same type of net charge, which indicates anomalous binding behavior between the two biopolymers which is the window between the two vertical arrows shown in Figure 6. Maximum yield of coacervate is obtained if these are collected near pH ≈5.4. The simple potential energy plot captures all the salient features of surface selective patch binding mechanism prevailing in the present system.
Figure 6: Electrostatic potential energy (in arbitrary units) between agar and gelatin molecules at intermolecular distance ds = 55nm. The zeta-potential plot of agar-gelatin intermolecular complexes and a titration plot is included for qualitative comparison of transition pHs. Notice that at pHC and pHΦ the potential energy undergoes abrupt change. Solid lines are guide to eye. Reproduced with permission from American Chemical Society [Boral et.al 2010].
Interaction among a set of four common biopolymers, Chitosan (C), agar (A), gelatin-A (GA), and gelatin-B(GB), were examined in different concentrations of solutions at room temperature in a systematic manner. This set was chosen using the following criteria: (i) GA and GB are polyampholytic (charge inversion at certain pH) and (ii) Chitosan (polycationic) and agar (polyanionic) have polyelectrolytic characteristics. The summary of the physical properties of these biopolymers is provided in Table 3.
| Material | Mol.wt./kDa | Persistence length/ nm | ξ/mV | Rh/nm | Rg/nm |
|---|---|---|---|---|---|
| Gelatin A | 100 | 10.0 | +7.0 | 58 | 55 |
| Gelatin B | 100 | 2.0 | +20.0 | 23 | 34 |
| Chitosan | 150 | 16.0 | +38.0 | 340 | 260 |
| Agar | 900 | 5.0 | -20.0 | 100 | 300 |
Table 3: List of physical properties of used biopolymers. The reported zeta potential values pertain to pH close to pHc. The full profile is shown in Figure 7. Reproduced with permission from Elsevier [95].
The pH-dependent surface charge attributes of these biomolecules was ascertained from the measurement of their zeta potential values. This is illustrated in Figure 7 which establishes the following: (i) Agar is a polyanion and chitosan is a polycation, (ii) pI of polyampholytes gelatin A and gelatin B are 9 and 5 respectively and (iii) chitosan surface charge is pH dependent while for agar it is independent. From this data, we can define the SPB regimes rather explicitly for our samples. It is useful to note that binding occurring between polymers carrying charge of same polarity is referred to as SPB. For GA-GB system interactions below pH 5 will be governed by SPB, for C-GA same will be true for pH below 9, for C-GB it will happen below pH 5 and for A-GB it will occur for bindings above pH 5. In summary, the interactions basically reduce to that between a PE and a PA. It has been observed that due to heterogeneous charge distribution found on protein surface, polyions (polyanions or polycations) selectively bind to oppositely charged surface patches of protein molecules through electrostatic interaction overcoming the repulsive interaction occurring between similarly charged surface patch and the polyion [62,67,71-73]. Thus, SPB has been largely observed in protein-PE based interactions.
Figure 7: The pH dependent variation of a) zeta potential ζ .for various biopolymers at room temperature. Arrows indicate pI values which is 9 and 5 for gelatin A and gelatin B molecules. Agar is a polyanion and chitosan is a polycation. b) Turbidity profiles are shown for various interacting biopolymers in their salt free solutions for measurements taken at room temperature. The alphabets A, B and C identify the locations on the curves where pHc, pHΦ and pHprep occur. For A-GB samples titrations were conducted from high to low pH whereas for other samples it was from low to high pH. See text for details. Reproduced with permission from Elsevier [Pathak et.al 2013].
Surface patch binding versus electrostatic interactions
The relative abundance of these interactions can be quantified from the observing the relative spread of SPB as compared to EB over entire binding pH regime (in pH units). In case of C-GA the entire pH-binding zone consisted of only surface patch binding. Therefore, the degree of SPB is 100% which is plotted against the surface charge ratio of the interacting biopolymer at pHc. Similarly, it was calculated for other interacting biopolymer pairs. On collating, we arrive at the surface patch binding profile shown in Figure 8.
Figure 8: Surface Patch Binding profile as function of charge ratio. and The 3D phase diagram blue layer shows pHc regions, green layer shows pHΦ regions and yellow layer shows pHprep regions in all biopolymer solutions. Individual phase diagrams are depicted in the electronic supporting information. Reproduced with permission from Elsevier [Pathak et.al 2013].
When a strongly charged polyanion interacts with a weakly charged polyion, it tends to attract many polyions to form a complex. We encountered the presence of a range of complexes that are partially to fully neutralized and overcharged entities. The first two complexes are electrostatically governed while secondary force dominates overcharging. It is useful to conjecture why disproportionate binding and overcharging may occur at all. During the binding process, a finite number of polyions get strongly adsorbed on to the surface of high charge density DNA molecule and produce a partially charge neutralized complex. This complex contains residual negative charge originating from exposed and unbound segments of DNA. As a result more polyion molecules continue to bind to this complex through electrostatic interactions until a physical situation arises where this hydrated complex becomes completely charge neutralized and no further electrostatic interactions is possible. It must be realized that at this instance, the DNA is fully coated with polyion molecules. Now the polyions bind with these charge- neutralized complexes through secondary forces like hydrogen bonding and hydrophobic interactions causing accumulation of excess positive charge on the surface of the complex. Based on the results in hand a schematic representation of overcharging in DNA-polyion complexation is proposed, which is shown in Figure 9. DNA being a long polyanion attracts many shorter polyions of different stiffness. As the stiffness of the polycation increases the number of polyions bound to the polyanion increases due their limited flexibility. Polyion with high persistence length binds heterogeneously to DNA, leading to inadequately Coating of the DNA. This inadequate coating facilitates the further binding of the polyions to the DNA chain which finally leads to the Overcharged complex. Hence the polyion with maximum stiffness is most overcharged among the polyions used. Based on the results in hand a schematic representation of IL-mediated DNA-protein complexation is proposed, which is shown in Figure 9.
Gelatin A- Gelatin B
The measured pH dependent titration profile of various biopolymer and their pairs in salt free solutions is depicted in Figure 10 which is very revealing. This figure assigns pHc, pHΦ and pHprep values equal to 3.8, 5.0 and 6.8 respectively. Since, the pI for GB is 5.0; associative interaction occurring between GA and GB at pHC was clearly of SPB type. This interaction continued until pH reached a value pHΦ =5.0. Beyond pHΦ aggressive binding prevailed driven by strong electrostatic interactions because GA and GB carried opposite charge. The blank solutions were stored for 24 hrs and no sign in change in turbidity was observed (data not shown).
Figure 10: pH-dependent zeta potential data for DNA and all polyions used in the present study is shown pertaining to measurements performed at 20 °C. Note the strong polyanionic nature of DNA, weak polycationic property of chitosan and polyampholytic behaviour of gelatin A and B, and BSA.. b) Plot of solution turbidity measured at 450 nm as function of pH. At pHc associative interactions ensued and soluble complexes were formed marked A, (ii) at pHΦ soluble complexes coalesced to give rise to liquid-liquid phase separation, marked B and (iii) at pHprep formation of large insoluble complexes drove the solution to liquid-solid phase separation, marked C. Here, DNA concentration was maintained at 0.05% for GA and 0.5% for others. While polyion concentration used are 0.1% for GA, GB and BSA and 0.05% for chitosan. All measurements were performed at room temperature 20 °C. [Rawat et.al 2013] - Reproduced by permission of the PCCP Owner Societies.
In the next step, the titrations were carried out in solutions having ionic strength in the range I= 5-300 mM NaCl (data not shown) and the aforesaid pHs were determined. No coacervation transition was noticed for I > 50 mM. The ionic strength dependent pHC, pHΦ and pHprep values are presented in Figure 11 which implies complete invariance. This interaction phase diagram clearly defines various interaction regimes prevailing in the solution phase. Note the soluble complexes were formed through SPB binding whereas EB dominated mesophase formation following coacervation transition occurring at pHΦ. The relative abundance of these interactions can be quantified from the observation that SPB was spread over one pH unit as compared to EB that spanned over two pH units, this will be discuss later.
Figure 11: Interaction phase diagram of a) C-GA system b) GA-GB systems clearly defining various interaction regimes prevailing in the solution. Note the soluble complexes were formed through SPB binding whereas EB dominated mesophase formation following coacervation transition. Solid lines are guide to the eye only. Reproduced with permission from Elsevier [Pathak et.al 2013].
The acid-base equilibria of the PA molecules can also get altered giving rise to modified charged states. Both the aforesaid phenomena will have profound effect on PE-PA binding [1]. EB is well known to be both ionic strength and temperature dependent a manifestation of which should have been reflected in the pHΦ and pHprep data. It must also be realised that temperature alters the geometrical configuration of a flexible polymer (polyampholyte in our case). However, preliminary investigation of the system revealed a very weak temperature dependence of binding behaviour (pHC, pHΦ and pHprep) in a narrow range of temperature spread (25-40°C). However, detailed investigation is required to establish this observation which is under way. Since, pHΦ resided within 0.5 unit of pI of GB; it can be safely argued that formation of soluble complex was fully guided by SPB interactions whereas electrostatic binding caused mesophase separation.
Chitosan-Gelatin A
The zeta potential profile shown in Figure 10a attributed polycation feature to chitosan, but GA was associated with net positive charge below pH 9. The pH versus solution turbidity profile depicted in Figure 10 b illustrates pHC =3.7, pHΦ=6.0 and pHprep=8. Thus, the entire interaction regime resided in the SPB region comfortably. The soluble complexes were formed in the wide region lying between pH 3.5 and 6.0, and the mesophase region prevailed between pH 6 and 8. The ionic strength dependent titrations carried out at room temperature generated a phase diagram shown in Figure 11b. Alike in the GA-GB case, all the transition pHs remained invariant of ionic strength for I<50 mM NaCl and no coacervation was noticed for I > 50 mM.
It is clearly seen that a polyelectrolyte, chitosan and a polyampholyte, gelatin A can follow associative interaction culminating in coacervation transition and such a process is driven by charge selective patch binding mechanism. It implies that though the net charge on GA was positive at pHC it had significant amount of negatively charged surface patches to facilitate selective binding with positively charged chitosan molecules overcoming the electrostatic repulsion between positively charged segments of GA with that of chitosan. Obviously, surface selective binding would be enhanced by increase in the flexibility of the polyion. The polyion (chitosan) is likely to have a large persistence length compared to GA because of the high charge density associated with this molecule. In spite of this, the system could be driven towards coacervation following all the characteristic pathways that are normally associated with the phenomena of coacervation transition [32].
Chitosan-Gelatin B
Gelatin B is associated with a pI=5.0 and as mentioned earlier while chitosan is a polycation. The titration profile presented in Figure 12a gives pHC =3.5, pHΦ=5.4 and pHprep=7.3. Thus during the course of titration soluble complexes were initially formed in the pH region 3.5 to 5 through SPB and between pH 5 and 5.4 the same continued through electrostatic interactions. Mesophase separation clearly occurred in the pH region 5.4 to 7.3 where EB was the dominant force because chitosan and gelatin B carried charge of opposite polarity in this region. The solution ionic strength was varied as before and for each ionic strength pH titrations were performed to determine the corresponding transition pHS. We continued to observe independence of pHC, pHΦ and pHprep as function of solution ionic strength for I < 50 mM NaCl and for I > 50 mM no coacervation was noticed. The interaction phase diagram revealing these features is shown in Figure 12a.
Figure 12: Interaction phase diagram of a) C-GB system and b) Agar-GB system clearly defining various interaction regimes prevailing in the solution. Note the soluble complexes were formed initially through SPB binding and later through EB. Electrostatic interactions continued to dominate mesophase formation following coacervation transition. Solid lines are guide to the eye only. Reproduced with permission from Elsevier [Pathak et.al 2013].
Agar-Gelatin B
Agar is a high charge density polyanion and is a strong polyelectrolyte. Thus, it can bind to a polyampholyte molecule like gelatin B with relative ease. The pH versus turbidity profile shown in Figure 12b adequately testifies this. In these measurements, during the titration, the pHC was approached from basic pH, unlike all other cases where the same was approached from acid pH side. The characteristic transition pHs were found to be pHC =7.8, pHΦ=5.1 and pHprep=3.7. Thus, the SPB was operative in a large pH window of close to 3 pH units in the present case. Mesophase separation driven by EB, in contrast, was observed between 5.1 and 3.7, a very narrow range indeed. Regardless, it must be realized that due to high charge density of agar molecule it could bind aggressively to GB for pH > 5.
These solutions were examined in presence of NaCl concentration ranging between 5-300 mM. The results obtained was same as reported for other systems, no variance of pHC , pHΦ and pHprep for I < 50 mM and no coacervation for solutions having ionic strength greater than 50 mM. Figure 12b clearly illustrates the ionic strength independence of these transition pHs. The binding process started with the surface selective patch binding when both the molecules, agar and gelatin, had a majority of negative charge on them, followed by partial charge neutralization and aggregation of coacervate droplets to form the mesophase. Since the agar molecule is stiffer than the gelatin molecule, the surface selective area (positive charge patch) of gelatin molecule binds over the agar rigid rod and partial charge neutralization takes place. On reaching the pI of gelatin, the gelatin molecule acquires more positive charge for the charge neutralization to proceed more aggressively following electrostatic binding.
DNA-Gelatin B / Aqueous medium
Experiments were performed in two distinct steps: (i) DNApolyion binding study was carried out in aqueous media; and (ii) in the second step optimum IL concentration was determined pertaining to optimum DNA-polyion binding condition. The objective was to record differential binding pattern and overcharging behaviour explicitly. In the first step, we configured the DNA-polyion interaction prevailing in aqueous environment by looking at the binding profile as function of pH for a given polyion concentration, and as function of polyion concentration at pHC, where intermolecular interactions ensue. The first signature of intermolecular associative interaction was obtained from measurement of solution turbidity. The simplicity and sensitivity of turbidimitric titration method as applied to DNA-polyion systems is based on the fact that turbidity is proportional to both the molecular weight and the number density of particles present in dispersion.
Gelatin B (GB) is a flexible chain of low charge density and small persistence length. Light scattering measurements assigned the following dimensions [14] (radius of gyration, Rg and hydrodynamic radius, Rh) to the GB chains: Rg = 34±3 nm, Rh= 23±3 nm. Thus, one can estimate the chain stiffness from the ratio [74] Rh/Rg which 0.67 for gelatin-B. This clearly attributes a fully flexible chain conformation to GB. The maximum and minimum zeta potentials were observed at pHs 3 and 8 were + 30 mV and -24 mV respectively. Figure 10 depicts the pH dependent binding profile of DNA with GB at room temperature which identifies the three characteristic pHs where specific associative transitions occurred. At pHC = 6.3 associative interactions ensued and soluble complexes were formed, (ii) at pHΦ = 4.2 soluble complexes coalesced to give rise to liquid-liquid phase separation (coacervation) and (iii) at pHprep=3.8 formation of large insoluble complexes drove the solution to liquid-solid phase separation. These pHs are designated as A, B and C on the curves. Thus, the pHC was more than pI = 4.9 of this protein. The persistence length ratio DNA: GB was 50:2 whereas the charge ratio at pHC was (70:5) (in zeta potential units).
Hence, the net charge on GB at this pH was negative; regardless of this there was associative interaction between GB and negatively charged DNA molecule that facilitated formation of intermolecular soluble complexes. This is due to the fact that the positive and negatively charged patches are inhomogeneously distributed along the contour of GB chain which facilitated surface patch selective binding where the positively charged patches selectively remained attached to DNA strand overcoming the repulsion occurring between negatively charged patches of GB and DNA.
This is further elucidated in Figure 13 where the size of intermolecular complexes and zeta potential of these, measured at pHC, are shown as function of protein concentration. Three clearly identifiable binding regions are established from this data: (i) Region-I, CGB <0.05 %, is characterized by rapid growth in the size (from 200 to 1400 nm) of complexes associated with significant charge neutralization ( ζ reduced from -70 mV to -3 mV) arising due to GB binding to DNA, (ii) Region-II, 0.05
Figure 13: Plot of hydrodynamic size and zeta potential of DNA-GB intermolecular complexes without and with 0.05% [C8mim][Cl] solutions at pHc where associative interactions ensue and soluble complexes are formed. Charge reversal and overcharging is clearly seen in Region-III. All measurements were performed at room temperature 20 °C. Here, DNA concentration was fixed at 0.05%. Dotted line defines complete charge neutrality. Solid lines are guide to the eye. [Rawat et.al 2013] - Reproduced by permission of the PCCP Owner Societies.
DNA-Gelatin B / IL solutions: Addition of IL to water creates a heterogeneous media where liquid-liquid phase equilibria have been observed to be strongly hierarchical with IL concentration [47]. This is because; a molecule like 1-methyl-3-octyl imidazolium chloride ionic liquid can interact with water molecules through hydrogen bonding, hydrophobic interactions and ionic interactions simultaneously. The interplay of these forces causes regions of IL-rich and IL-poor domains in the IL solution. Thus, the DNA-polyion binding mechanism in such solvent environment will be qualitatively different from that in water which was clearly noticed from the following studies.
Figure 14 displays the solution turbidity as function of IL concentration for DNA-polyion interaction occurring in IL solutions. During these experiments the DNA to polyion concentration ratio was maintained at their optimum value (0.005% DNA and 0.1 % GB). The turbidity maximum for DNA-GB system was observed at IL concentration 0.05 % which is shown as Region-I in the figure. Below this concentration, turbidity increased rapidly implying formation of bigger soluble complexes with rise in IL concentration. This process reached a maximum at [IL]=0.05%. Beyond this concentration (Region-II), the depletion in turbidity ensued implying formation of large insoluble complexes for all polyions.
Figure 14: Plot of solution turbidity measured at 450 nm as function of [C8mim][Cl] concentration at pHc. Maximum associative interaction was noticed at 0.05% IL concentration. DNA concentration was maintained at 0.005% for GA and 0.05% for others polyions. Polyion concentrations were fixed at 0.1% for GA, GB and GB. In case of chitosan, it was fixed at 0.05%. All measurements were performed at room temperature 200 C. Region-I is characterized by formation of soluble complexes that are precursors to liquidliquid phase separation and in Region-II these complexes coalesce to form large in soluble complexes. [Rawat et.al 2013] - Reproduced by permission of the PCCP Owner Societies.
In the next step, we varied the concentration of polyion in 0.05% IL solution and monitored the turbidity to determine optimum binding ratio between DNA and polyion (Figure 15). Region-I depicts IL assisted formation of large soluble complexes for all the samples which reached a maximum for chitosan at a concentration 0.05% whereas for all others this was found to be 0.075%. Region-II in this plot is quite revealing. It is clearly seen that at higher GA and chitosan concentration the turbidity of samples remained invariant. This is due to the fact that DNA-GA and DNA-chitosan complexes were overcharged and remained in suspension due to mutual repulsion. For BSA and GB samples the overcharging was marginal so the abovementioned phenomenon though present was much reduced.
Figure 15: Plot of solution turbidity measured at 450 nm as function of polyion concentration with the IL concentration fixed at 0.05%. DNA concentration was maintained at 0.005% for GA and 0.05% for others polyions while polyion concentration was varied from 0-5%. Maximum associative interaction was noticed at 0.05% for Chitosan whereas for others it was noticed at 0.075%. Region-I is characterized by formation of soluble complexes. In Region-II, GA and chitosan follow one pattern while GB and BSA show a different behaviour. All measurements were performed at pHc. [Rawat et.al 2013] - Reproduced by permission of the PCCP Owner Societies.
The quantitative estimation of complex size and its zeta potential was systematically carried out using DLS and electrophoresis measurements. This data is shown in Figure 14 and 15 where polyion concentration dependent hierarchical binding is clearly manifested. For CGB<0.1%, one observed ten-fold increase in size of the complex with substantial charge neutralization (Region-I).
Between GB concentration 0.1 to 0.2 %, both the complex size and zeta potential remained invariant of protein concentration (Region- II). In Region –III, the complexes were found to be positively charged and the extent of overcharging in IL solutions was less than that found in water, a conclusion that is drawn from comparing Figures 13. This could be arising from disproportionate binding of imidazolium cations to DNA-GB complexes occurring at high protein concentration. The reduction in overcharging was to the tune of 20 %. However, the size of the complexes revealed an increase of about 10% due to the aforesaid binding. In high GB concentration regime (CGB>0.2%), the large size complexes precipitated out of the solution and only complexes of size few hundred nanometres were sustained in the dispersion phase.
DNA- BSA / aqueous medium
BSA has shown binding affinity towards many synthetic polyelectrolytes like [75] poly(diallyldimethylammonium chloride), Sodium poly(styrenesulfonate), Sodium poly(viny1 sulfate), Sodium poly(2-acrylamidomethylpropylsulfate) etc. Thus, it binds to polymer chains of various chain length, persistence length and linear charge density. Figure 10 illustrates the pH dependent binding profile observed through turbidity studies. The state of macromolecular assembly of complexes formed between a pair of complementary polyelectrolytes, (BSA and DNA in our case) prior to and during pH-induced coacervation at constant mixing ratio could be characterized by specific pH values at which recognizable transitions took place [32]. Based on the pHinduced evolution of turbidity measurements, we observed two well defined points, pHC and pHΦ, corresponding to the formation of soluble primary protein-polymer complexes and subsequent microscopic liquid-liquid phase separation. The characteristic pHs where binding transitions occurred were pHC=7 and pHΦ=5.3. Thus, pHC was greater than pI=4.8 implying overall negative charge for BSA and its successful binding to DNA molecule. Even coacervation transition signified by pHΦ occurred above isoelectric pH indicating the play of surface patch binding in this system.
Figure 16 depicts the size and zeta potential of DNA-BSA intermolecular complex as function of protein concentration. In the low protein concentration region, Region-I (CBSA < 0.05%), soluble complexes of higher size and low zeta potential were preferentially formed with increasing BSA content until the mean complex size reached a value ≈1300 nm where these entities were found to be either completely charge neutralized or carrying negligible amount of surface charge. In Region II which prevails in the BSA concentration range 0.05 < CBSA <0.15%, both the complex size (≈1300 nm) and its zeta potential (≈ -3 to 4 mV) remained invariant of protein concentration; a stable dispersion was sustained. Region-III pertaining to the concentration regime CBSA >0.15% is signified by observation of polarity reversal of the complexes and their overcharging behaviour. The complexes were associated with zeta potential ≈14 mV. This region is designated as a disproportionate binding region.
Figure 16: Variation in size of DNA-BSA complex as function of protein concentration without and with 0.05% [C8mim][Cl] solutions at pHc. Here, DNA concentration was maintained at 0.05%. Note the overcharging of complexes for BSA concentration exceeding 0.15%. Arrows indicate various binding regions. See text for details. [Rawat et.al 2013] - Reproduced by permission of the PCCP Owner Societies.
DNA-BSA / IL solution: Figure 14 illustrates maximum intermolecular complexation between DNA and BSA at IL concentration 0.05%. Below this concentration (Region-I), binding of imidazolium cations to DNA-BSA complexes facilitated generation of large size complexes that was manifested in appearance of high turbidity. In Region-II pertaining to IL concentration more than 0.05%, turbidity decreased because of the liquid-solid phase separation of large complexes from the solution. After establishing the IL concentration where binding was maximum, it was imperative to examine the effect of protein concentration on the binding profile. This data is shown in Figure 15. Alike in the case of DNA-GB system, for protein concentration less than 0.075%, intermolecular complexation was enhanced in IL environment whereas above this concentration phase separation of large size complexes resulted in the retention of smaller complexes only in the dispersion, thereby, decreasing the turbidity.
A quantitative estimation of this is provided in data presented in Figure 6. Enhanced formation of DNA-BSA complexes were observed for protein concentration less than 0.05% in IL solutions (Region-I). Here the size of the complex increased by 10-fold alike in the case of DNA-GB system. This process was accompanied by significant charge neutralization of these complexes. In the protein concentration region between 0.075 to 0.15%, the size of the complexes and their zeta potentials remained invariant of concentration (Region-II). Complete charge neutral complexes were observed when BSA concentration was close to 0.15%. Beyond this concentration, marginally overcharged complexes were noticed. However, large complexes were not sustained in the dispersion. One qualitatively observed identical features in protein concentration dependent DNA-GB and DNA-BSA binding profiles, a conclusion that has been drawn from comparing Figures 16.
DNA-Gelatin A / Aqueous medium
Compared to gelatin B, gelatin A is a stiffer polyampholyte with a larger persistence length (lp = 10 nm). Light scattering measurements assigned the following dimensions to the GA chains: Rg = 55±5 nm and Rh= 58±6 nm. Thus, the chain stiffness determined from the ratio [14] Rh/Rg was 0.95. This clearly attributes a less flexible chain conformation compared to gelatin-B. Thus, DNA and Gelatin A (GA) had characteristic charge ratio (DNA: GA=16:1) and persistence length ratio (5:1). Charge ratio was estimated from their measured zeta potential data. The binding profile shown in Figure 10 established the following characteristic binding pHs where specific interactions lead to the pathway of coacervation transition: pHc = 8.2, pHΦ=6.5 and pHprep=5.8. The pI of this protein is 9.0 which indicate at the initiation of interaction the binding was predominantly electrostatic and the same continued all through.
Figure 17 provides a clear depiction of dependence of hydrodynamic radii and zeta potential of the soluble complexes at the pHc. A closer examination of Region I, (CGA<0.05%), reveals that in this region as the protein concentration was increased the zeta potential decreased from -75 to -20 mV (70%) and hydrodynamic radii of the complex decreased by close to 60% (from 140 nm to 60 nm). Thus, the solution contained DNA-GA complexes that had size less than that of pristine DNA. Moreover, these complexes carried reduced surface charge. In other words, binding of GA to DNA caused the latter to shrink in size (chain softening). There is a characteristic difference between the Region-I data shown in Figures 17. DNA-GB complex formation did not cause the aforesaid chain softening.
Figure 17: Plot of hydrodynamic size and zeta potential of DNA-GA intermolecular complexes without and with 0.05% [C8mim][Cl] solutions at pHc where associative interactions ensue and soluble complexes are formed. Here, DNA concentration was fixed at 0.005%. Note the DNA chain softening due to binding with GA in Region-I. Charge reversal and overcharging is clearly seen in Region-III. Dotted line defines complete charge neutrality. Solid lines are guide to the eye. [Rawat et.al 2013] - Reproduced by permission of the PCCP Owner Societies.
Condensation of DNA is known to arise from two important mechanisms: phosphate charge neutralization of DNA molecule and /or reduction of water activity through the reduction in dielectric constant of the medium. Manning’s condensation theory clearly explains cationinduced condensation of DNA molecules mostly by neutralizing phosphate charge [76,77]. It was also shown that condensation ensued when ~ 80% of the charge was neutralized. Substantial folding of high molecular weight DNA could be observed in presence of polylysine and polyethylene oxide molecules [78]. Interestingly, even nonpolar molecules like polyvinyl pyrrolidinone influence DNA folding [79]. Thus, it is believed that several factors favour DNA condensation and aggregation, in addition to electrostatic forces, which include hydration forces and cross-linking by condensing ligands [80,81]. In the present case it is plausible that DNA and GA molecules bind through a similar mechanism where close to 70% charge neutralization was achieved.
In contrast Region-II, (0.05
DNA-gelatin A / IL solution: The binding profile presented in Figure 14 indicates maximum binding between DNA and GA at IL concentration 0.05% alike DNA-GB and DNA-BSA systems. Here too one observed enhanced intermolecular associations when IL concentration was less than 0.05% (Region-I). In Region-II, the turbidity value decreased by typically 10% in the entire IL concentration region explored. We shall see it later that this had bearing on charge reversal and overcharging of DNA-GA complexes. Figure 15 data conclude that in low protein concentration region (CGA < 0.075%) presence of IL in the solution facilitated formation of larger complexes. Complex size reached a maximum at protein concentration 0.075% (Region-I). Beyond this concentration, addition of more proteins helped generation of even larger complexes that were unsustainable in the dispersion (Region-II). This was further elucidated in quantitative results obtained from measurements performed on these systems the data for which is shown in Figure 18.
Figure 18: Variation in size of DNA-chitosan complex as function of protein concentration in 0.05% [C8mim][Cl] solutions at pHc. Here, DNA concentration was maintained at 0.05%. Note the overcharging of omplexes for chitosan concentration exceeding 0.2%. Arrows indicate various binding regions. See text for details. [Rawat et.al 2013] - Reproduced by permission of the PCCP Owner Societies.
A detailed work on DNA-GA intermolecular interaction studies has been reported by us earlier [47]. Herein, we recapitulate some salient features pertaining to protein concentration dependence of this interaction in IL solutions.
A closer examination of Region I reveals that in this region as the protein concentration was increased the turbidity increased by 40%, zeta potential decreased from -80 to -5 mV (95%) and hydrodynamic radii of the complex decreased by close to 60%. Thus, the solution contained DNA-IL-GA complexes that had size less than that of pristine DNA, moreover, these complexes carried marginal surface charge. This binding between the nucleic acid and the protein molecule mediated by the IL resulted in making the DNA molecule compact. It must be realized that the pH of the DNA, GA and IL interacting solution was 6.0±0.5 where DNA molecules were anionic and protein was cationic (pI ≈9.0). This facilitated strong Coulombic interaction between the biopolymers though limited to screening by the presence of IL molecules.
In Region-II, as the concentration of GA was increased the solution properties changed significantly. It is seen from Figure 18 that significant change in solution properties was observed for 0.075 < CGA < 0.125%, the turbidity increased two-fold, zeta potential decreased from -5 mV to zero (complete charge neutralization) and hydrodynamic radii increased three-fold. Appearance of charge neutralized soluble complexes and sharp rise in turbidity. In this narrow GA concentration range the protein molecules aggressively bind to DNA facilitated by the presence of IL molecules.
For 0.125
DNA-Chitosan / Aqueous medium
Chitosan (poly [β-(1-4)-2-amino-2-deoxy-D-glucopyranose]) is a biodegradable cationic polysaccharide produced by partial deacetylation of chitin derived from naturally occurring crustacean shells. Chitosan is also found in various fungi. The molecular formula is C6H11O4N. The polymer is comprised of copolymers of glucosamine and N-acetyl glucosamine. Despite its biocompatibility, the use of chitosan in biomedical fields is limited by its poor solubility in physiological media. Chitosan has an apparent pKa value between 5.5 and 6.5 and upon dissolution in acid media the amino groups of the biopolymer are protonated rendering the molecule positively charged. At neutral and alkaline pH, most chitosan molecules lose their charge and precipitate from solution [20]
The pH-turbidity profile shown in Figure 10 for DNA-chitosan systems reveals the following characteristic pHs: pHC=9.3, pHΦ=7 and pHprep=6.4. The pH dependent zeta potential data shows (Figures 10) that chitosan is associated with very small positive zeta potential above pH =7 regardless, electrostatic interaction of this with DNA caused the formation of soluble complexes. The persistence length ratio DNA:chitosan was (50:16) and the charge ratio was (14:1) (in units of zeta potential). The binding profile was flat in the pH region 6.4 to 3 which indicated saturation binding.
The polyion content dependent binding profile of DNA to chitosan is clearly shown in Figure 15 where the variation in the size of the intermolecular complex and its zeta potential is plotted as function of chitosan concentration. The binding domain has been split into three distinct regions: (i) Region-I prevailed for Cchitosan <0.03% where the size of the DNA-Chitosan complex reduced from 140 to 95 nm (≈ 32 %) causing softening of DNA chain due to its binding with the polyion. As a result significant decrease in the value of the zeta potential, from -70 mV to -12 mV (≈ 85%) was noticed implying the occurrence of considerable charge neutralization. Such a situation, as argued earlier, would cause the DNA molecule to condense which was observed (note the reduction in Rh value). Since DNA and chitosan happen to be complementary polyelectrolytes, they interact very strongly through electrostatic forces, (ii) the concentration regime 0.3
There are following commonalities between the DNA-GA and DNAchitosan associations: (i) associative interactions were electrostatic, (ii) DNA condensation was observed in both cases and (iii) overcharging of the complexes was accompanied by loss in their size.
DNA-chitosan / IL solution: Chitosan was the only polysaccharide used in this work because a protein with long persistence length was hard to find. Chitosan is a polycationic molecule in the pH range 4-9 which makes it amenable to binding to a strong polyanionic molecule like DNA. However, in IL solutions screening of Coulomb interaction is expected and binding should depend on IL concentration. The pH dependent binding profile is depicted in Figure 14 where IL concentration was varied. Like other polyions, chitosan too was found to exhibit maximum binding with DNA at [IL] = 0.05%. Below this concentration (Region-I), presence of IL molecules in the dispersion helped formation of larger DNA-chitosan complexes which recorded a maxima at the aforesaid IL concentration. Many of these complexes grew even bigger when [IL] > 0.05%; however, such large size complexes were unsustainable in the dispersion and these phase separated causing the turbidity to deplete. This is clearly observed from the Region-II data shown in Figure 14.
The effect of polyion concentration on binding equilibria in IL solutions was established by measuring solution turbidity as function of chitosan concentration the data for which is shown in Figure 15. In Region-I like other polyions, chitosan was found to bind preferentially to DNA in presence of IL molecules and the propensity of this increased with chitosan concentration. Maximum turbidity signifying saturation binding was noticed at Cchitosan=0.05% whereas for other polyions this occurred at a concentration of 0.075%. This difference must owe its origin to the comparatively large persistence length of chitosan molecule. A quantitative estimation of this is provided in the data presented in Figure 18.
There are three distinct binding regions in this plot. In Region-I, Cchitosan <0.025%, partially charge neutralized DNA-chitosan complexes were formed preferentially. In a narrow concentration region 0.025 %
Dependence of phase diagram and overcharging on persistence length: In these studies, we have encountered two distinct types of associative interactions that yielded the formation of DNA-polyion complexes: (i) surface patch binding interaction between similarly charged macromolecules prevalent in DNA-GB and DNA-BSA systems and (ii) electrostatic interaction between oppositely charged macromolecules which was operative in DNA-GA and DNA-chitosan systems. The clearly identifiable pHs where characteristic interactions occurred are marked as A, B and C in Figure 10 which correspond to pHC, pHΦ and pHprep respectively. Figure 19 is a plot of these parameters as function of persistence length of the polyions which is very revealing.
Figure 19: a) Characteristic binding pHs plotted as function of polyion persistence length. The vertical line separates the two distinct interaction regimes. The shaded region depicts surface patch binding domain. b) Amount of overcharge associated with DNA-polyion complexes shown as function of polyion persistence length. The vertical line separates the two distinct interaction regimes. [Rawat et.al 2013] - Reproduced by permission of the PCCP Owner Societies.
This universal interaction phase diagram encompasses both the aforesaid binding mechanisms and implies that surface patch binding is common in small persistence length polyions whereas large persistence length polyions prefer electrostatic binding. Such an observation is qualitatively sustainable because for surface patch binding the polyion has to be extremely flexible to allow surface selective interaction which is difficult to achieve in stiff polyions. The vertical line in Figure 19a separates the two binding regimes and is indicative only. Further, we have plotted the amount of overcharge as function of polyion persistence length in Figure 19b for complexes formed in both aqueous and IL solutions. This too provides a universal depiction of dependence of overcharge on persistence length. Two conclusions are drawn from here: (i) overcharging is small in intermolecular complexes having flexible polyions and (ii) IL acts as an electrolyte and screens the overcharge.
Characterization of coacervates
After probing the intermolecular interactions responsible for coacervation transitions in this system it was felt imperative to undertake a thorough thermo-mechanical characterization of the polymer-rich phase of the reacted solutions (coacervates). While the viscoelastic properties including the melting behaviour were studied by rheology, the internal microstructure was examined through SANS experiments.
Melting temperature
Temperature sweep studies were performed on the extracted coacervate material where the temperature dependence of storage modulus was measured at a fixed frequency (6.2830 Hz) and the data is depicted in Figure 20. The melting temperature corresponds to the abrupt fall in the storage modulus value which is best noticed if the first derivative of G’ (dG’/dT) is plotted against the temperature (inset of Figure 20).
Figure 20: Plot of storage modulus, G’ as function of temperature for coacervate samples. A sharp drop in G’ value indicates a melting transition. The temperature derivative of G’ is shown in the inset where peaks indicate melting temperature.Solid lines are guide to the eye. Reproduced with permission from American Chemical Society [Boral et.al 2010].
The melting temperature for the system was around 75°C which was different from the gels of its constituents. No melting was observed around 30 or 85°C which correspond to gelatin and agar gel melting temperatures [82,83]. Thus, the coacervate material was a new biomaterial bearing no physico-chemical resemblance with its constituent biopolymers. The melting temperature is observed to increase with ionic strength by as much as 10°C. This may be due to formation of salt-bridges in the system that increases the mechanical rigidity of the material. On comparing these results with agar gels, one can also argue that such behavior owes its origin to the presence of gellike (physical) network structures inside the coacervate phase.
Viscoelastic behavior
Figure 21a shows the frequency sweep studies performed on the various coacervate samples at 20°C. The data indicates that though the dispersion behaviour was qualitatively similar the samples with higher ionic strength were associated with higher storage modulii again implying that the mobile ions established salt-bridges between the biopolymers to enhance the mechanical rigidity of the material. Figure 21b shows the frequency sweep curves at different temperatures (20-35°C) for no salt sample. Other samples showed similar frequency dependence. The linear viscoelasticity model, for pre- and post-gel situations, proposed by Winter [84] predicts that the stress-relaxation in the material allows the storage modulus to follow the power-law frequency dependence behavior given by
G’= Sωn with 0 < n <1 (7)
Figure 21: a) Frequency sweep plots of coacervate sample at various salt concentrations taken at temperatures 20 °C. These data fitted very well to power-law function (solid lines). See text for details. b) Frequency sweep plots at various temperatures 20, 25, 30 and 35 °C are shown for a salt free coacervate material. Solid lines are power-law fitting to the data that yields the power-law exponent n and rigidity strength of the material, S. Reproduced with permission from American Chemical Society [Boral et.al 2010].
Where, S is the elastic strength of the material and n is the exponent indicative of the nature of cross-linking. If n <0.5 it shows an excess of cross linker and when n> 0.5 there is a lack of cross linker. However, this formalism is strictly applicable to chemically cross-linked gels and strictly speaking our system is different from that of the system of gels. In the present samples, the crosslinking is provided by surface patch binding. The G’ values could be measured in a very narrow frequency range, 0.1-20 rad/s, with reliability. This value remained close to few hundred Pa for all the samples. The G’’ data was extremely noisy and unrealistically small. The plateau region in G’ is normally observed for strongly crosslinked chemical gels. In case of physical gels such a region is often not seen. We have treated the coacervate materials as a poorly crosslinked gels due to the fact that these yielded measurable G’ values that were consistently larger than G’’ data. The data shown in Figure 21b was fitted to equation 7 that yielded the exponent n. This exponent was determined to be ≈ 0.1 implying the existence of a weakly cross-linked system (Figure 9). The coacervate system is highly rich in polymers as compared to gels and lacks in free solvent diffusion process within the network.
Pierce and Carey [85] studied the flow of fluids in a host medium containing obstacles. Following their model it can be argued that the no-slip condition at the interfaces tends to force the water to move with the network, but the finite viscosity allows the water at small distances from the interfaces to move at a different velocity than the networks. The apparent driving force for the interstitial water relative to the networks is associated with the inertia of the water and is proportional to the difference in densities which attributes a different viscosity to interstitial as compared to bulk water. Coacervates trap some amount of interstitial water molecules whose viscosity can be imagined to be much higher than the water trapped inside the gel network. The Winter model [84] is applied to the rheological data obtained from coacervate samples in order to have a feeling of the elastic nature of the system. In short, one can easily assure oneself that the presence of salt increases the cross-linking inside the system as expected.
The viscoelastic length L was determined (Figure 22) from the relation [86]
G0=KBT/L3 (8)
where KB is Boltzmann constant, T is absolute temperature and G0 is the elastic storage modulus at low frequency where ω=0.1 rad/ sec. The viscoelastic length (typical distance between polymer-rich and polymer-poor regions, the values remained within the window 32- 22 nm) for the coacervate samples was found to be almost invariant of temperature, but it was strongly dependent on ionic strength. The viscoelastic length decreased with increased mobile ion concentration indicating that at higher ionic strength the biopolymers were strongly bridged. Hence, the gel strength was also found to be independent of temperature, but it increased with increase in NaCl concentration. Here too we can see the footprint of salt-bridges that helped to strengthen the coacervate systems. This clearly shows the role played by mobile ions in stabilizing the internal micro-structure of coacervates.
Internal Structure
In the Small angle neutron scattering (SANS) studies, the mean field theory reveals that polymers in a good solvent at equilibrium show a structure factor arising from concentration fluctuations in the intermediate-q region, known as Ornstein-Zernike (O-Z) function, which is given by [87]
SL(q)=SL(0)/ (1+q2ξ2) ; qξ>>1 (9)
Where, ξ is the correlation length of the fluctuations and it can be associated with the size of the entangled network. Physically SL(0) is related to the cross-linking density and longitudinal osmotic modulus of the network. If the spatial scale of density fluctuations due to the presence of inhomogeneities is large compared to the correlation length ξ, then the two contributions can be treated separately and an additional contribution to structure factor, Sex,(q) arises from long length scale concentration fluctuations (small-q). Thus the total structure factor can be written as [86-88]
S(q)=SL(q) + Sex(q) (10)
where SL(q) is the Ornstein-Zernike (O-Z) function, and the Debye- Bueche (D-B) structure factor has Sex(q) is given by [88]
Sex(q)=Sex(0) / (1+q2ζ2)2 (11)
where Sex(0) is the extrapolated structure factor at zero wave vector and ζ is the size of inhomogeneities present in the system. As Sex(q) α 1/q4, the D-B contribution dominates over O-Z function at low-q, whereas at intermediate-q, (SL(q) α 1/q2), O-Z function contributes the most to the scatter. Recall that coacervates are amorphous substances, and devoid of any spatial ordering (coacervation transition is a 1st order phase transition). This would imply identical scattering profiles for all the samples which will be observed if and only if the intermolecular interactions are so strong that mobile ion induced Debye-Huckel screening is not too effective. Since S(q) depends on the square of the difference of neutron scattering length densities of the scatterer and the solvent, it cannot distinguish between microscopic structures of two samples with identical concentrations, particularly when both are amorphous materials. A typical SANS plot is shown in Figure 23a.
The SANS data, collected at room temperature, was fitted to the O-Z function in the wave vector region 7.2 x 10-2 ≤ q ≤ 3.4 x 10-1(Å)-1 and to D-B function in the region 1.8 x 10-2 ≤ q ≤ 7.2 x 10-2 (Å)-1 (Figure 23a). This yielded the values for the correlation length and size of inhomogeneity which is shown in Figure 23b as function of salt concentration of the samples. The correlation length shows no dependence on ionic strength whereas the size of inhomogeneity increased by close to 50 %. Thus, the presence of mobile ions contributed to the increase in heterogeneity inside the coacervate.
Figure 23: a) Typical SANS experimental data of the coacervate sample (I= 0.1 M NaCl) recorded at 20 °C. Solid line is fitting to D-B and O-Z equations with χ2 > 0.9. See text for details. b) The plot depicts the size of inhomogeneities and characteristic length for various coacervate samples determined from SANS data. Reproduced with permission from American Chemical Society [Boral et.al 2010].
Evaluation of small-angle neutron scattering (SANS) data is often complicated by multiple scattering effects if large particles of relatively high volume fraction have to be studied and dilution or contrast reduction is impossible. Multiple scattering corrections in small-angle neutron scattering experiments on such samples have been examined. Numerical calculations show that, for such typical experimental conditions, the second-order scattering is less than 2% of the first-order scattering for qL up to 10.0, where L the length that is being measured [89-94]. In our system, L ≈ 30 A0 and qmax is 0.3 (A0)-1 which satisfies the said condition. Thus, it was not necessary to undertake any correction for secondary scattering. Another issue that clouds SANS data concerns observation of correlation peak. The raw SANS data clearly showed the absence of correlation peak at low-q and scattering profiles for samples, with and without salt, were observed to be identical because no preferential spatial correlation develops in the material due to presence of mobile ions. However, the data yielded different inhomogeniety size and correlation length as the salt concentration was altered. The behaviour is typical of polymer gels (and their sols) which has been extensively reviewed by Hashimoto [91]. In fact Hashimoto has examined a host of soft matter systems, but none showed any correlation peak in the low-q region. Leisner and Imae [92] examined complex coacervation in polyglutamic acid-polyamido amine dendrimers by SAXS and light scattering. Here too no correlation peak was seen.
A comprehensive and systematic investigation of binding of DNA with four polyions, three of them polyampholytes (gelatin A and B, and BSA) and one a polyelectrolyte (chitosan), was performed in aqueous and in 1-methyl-3-octyl imidazolium chloride ionic liquid solutions. The aforesaid polyions had intrinsic persistence lengths in the range 2-16 nm as compared to that of 50 nm for DNA. The pH dependent binding profiles yielded characteristic pHs where identifiable intermolecular interactions occurred in aqueous reaction media. These pHs could to be correlated to persistence length with the distinction that low persistence length polyions preferentially interacted with DNA through surface patch binding mechanism whereas large persistence length polyions exhibited electrostatic binding with DNA. The crossover appears to be occurring at typical persistence length ≈ 10 nm in our case. This corresponds to DNA: polyion persistence length ratio ≈ 5:1. As the polyion concentration was increased beyond the concentration required to meet complete charge neutralization of the complexes, disproportionate binding of polyions to existing hydrated complexes was noticed in all cases. And all these complexes were overcharged. Three distinct physical observations could be made here: (i) the physical mechanism governing binding hierarchy is dependent on polyion persistence length, (ii) there was reversal of polarity of charge associated with these complexes due to disproportionate binding and (ii) all these complexes were considerably overcharged. In IL solutions, much of the same salient binding features were noticed. However, the quantum of overcharge was reduced by close to 80% in case of complexes containing low persistence length polyions and by approximately 65% for complexes having large persistence length polyions. Thus, the [C8mim][Cl] ionic liquid acted as an electrolyte and successfully screened the Coulombic interaction prevailing between DNA-polyion complexes and polyions. Interestingly, a plot of overcharge as function of polyion persistence length produced a smooth curve that indicated higher overcharging for large persistence length and vice versa [93,94].
Though presence of hydrogen bonding and hydrophobic sites on the polyions influence biomolecular binding, they hardly play any role in deciding the persistence length of the polyion unlike the surface charge. Interestingly, we observed that the differential binding (SPB versus EB) was found to be a function of intrinsic persistence length only which we conclude as a significant observation. It was observed from the experiments that disproportionate binding for polyampholyte molecules always occurred when solution pH was more than pI. In summary, it was observed that DNA experienced hierarchical binding with oppositely charged and similarly charged polyions depending on the persistence length of the polyion concerned. Moreover, DNApolyion associative interaction produced overcharged complexes in all the cases under consideration in this study [95]. There are many reports available in already Published Date: papers for more information on DNA binding and its application [96-102].
We have reported the systematic of little known interaction surface patch binding (SPB) mechanism operating between polyions which lead to intermolecular associative interactions and the consequent mesophase separation. The experimental data on hand allows the following universal salient features to be noticed: (i) SPB interactions were independent of salt concentration in the range 0 ≤ NaCl ≤ 50 mM, (ii) no coacervation transition was observed for NaCl ≥ 50mM, (iii) SPB interactions were weakly dependent on temperature and extensive study is required, (iv) the SPB index was a monotonously decreasing function of PA:PE charge ratio and (v) coacervate yield was directly proportional to SPB index. The comprehensive mapping of the mesophase transition pathways permitted the constructions of explicit phase diagrams of the four interacting macroion pairs undertaken in the present work. SPB interactions prevailed through attractive electrostatic forces operating between oppositely charged surface patches of polyions overcoming the repulsive interactions that result from similarly charged surface patches. Therefore, to quantify this interaction, the intermolecular interaction potential for pairs of complementary polyions was estimated from competing screened Coulombic interactions by assigning appropriate geometry and surface charge to these polyions. We have shown considerable qualitative agreement between our experimental and theoretical observations. Relative strength of SPB vis a vis EB was used as an index to establish a linear relationship with zeta potential ratio of binding partners. Phase diagrams for abovementioned systems could be constructed which clearly identified distinct interaction regimes encountered in solutions undergoing coacervation transition [102]. The present work provides a deeper understanding of the SPB interaction phenomena occurring in biopolymer systems.
A relative comparison of physico-mechanical properties of various coacervate systems is given in Table 4 [12]. These systems were probed by SANS and rheology experiments performed in our laboratory. Hydrophobic interactions in addition to that of electrostatic and solutesolvent interactions facilitate coacervation transition in gelatin solutions, which has been discussed in details in ref. [30,62]. The occurrence of phase separation in the system was attributed to the change in volume fraction of the non-solvent added to the homogeneous aqueous solution of gelatin. It was reported that the salt had promoted the coacervation process [30,62]. In gelatin A- gelatin B complex coacervate system [14], there was purely electrostatic interaction induced by pH change, which led to the liquid-liquid phase separation. However, the salt dependence was not reported in the literature. In case of gelatin-chitosan complex coacervation, the intermolecular association was initiated by surface selective patch binding followed by charge neutralization process [11]. The presence of salt had hardly any significant effect over the binding of the two biopolymers. The same type of qualitative behavior was observed in the present case and we noticed hardly any evidence of ionic strength in the binding process though the same affected the thermomechanical properties of coacervates considerably. The SANS data profile of different coacervate samples inferred similar static structure factors, however there was a variation in length scales in different systems. Our system had less heterogeneity and larger characteristic size as compared to that of the gelatin simple coacervate and its other complex coacervates discussed above. There were no reports for SANS study of gelatin A-gelatin B complex coacervates.
| System/ d (nm) | Interaction at | ||
|---|---|---|---|
| pHc | pHΦ | pHprep | |
| GA-GB/ 28.0 | 3.15/ Surface patch | 5.9/ Electrostatic | 6.9/ Electrostatic |
| GA-Chitosan/ 230.0 | 4.6/ Surface patch | 6.7/ Surface patch | 8.0/ Surface patch |
| GB- Chitosan/ 230.0 | 3.6/ Surface patch | 5.6/ Surface patch | 7.9/ Electrostatic |
| GB- Agar/ 60.0 | 7.6/ Surface patch | 6.3/ Electrostatic | 4.3/ Electrostatic |
Table 4: Comparison of interaction pH-values (pHc, pHΦ and pHprep) and interaction type and inter atomic distance of different Complex coacervates without salt. Reproduced with permission from Elsevier [95].
The melting temperature for the gelatin simple coacervate (33°C) was near the melting temperature of gelatin gel [82]. However, there was a significant shift to 42°C in case of gelatin-gelatin complex coacervate [14] which was due to the change in type of binding. In the gel system, network formation is due to hydrogen bonding, and in case of coacervates, it is due to electrostatic binding. The complex coacervate of gelatin is bonded more strongly than that of the simple coacervates. In the gelatin-chitosan complex coacervate there were two melting temperatures [11]. One of these was close to agar gel melting temperature [83] (≈ 85°C). In gelatin A-agar complex coacervate, there were also two melting temperatures, one being near to the melting temperature of gelatin gel [63] and the other at 75°C. However, in our present system, we recovered only one melting temperature near 75°C, which was different from the melting temperatures of its constituent polymer gels [82,83]. Hence, one can see some signature of gelatin gel in gelatin A- Agar complex coacervate system, but no signature of the same in gelatin-B-Agar complex coacervate. This indicates that there must be a differential binding mechanism and charge neutralization process between the agar and gelatin-B and agar-gelatin-A samples. It is concluded that the former is governed by surface selective patch binding while the later is due to pure Coulombic interactions.
The rheology studies on the gelatin simple coacervates [30,62], gelatin-chitosan complex coacervate [11] and gelatin-A-Agar complex coacervate [63] reported in literature reveals that they are viscous in nature, while the gelatin A-gelatin-B complex coacervate [14] and gelatin-B-agar complex coacervate are viscoelastic in nature. The correlation lengths measured in gelatin simple coacervates was same as that recorded in gelatin-chitosan and gelatin-A-agar complex coacervates (≈1.2 nm) while the size of inhomogeneities ranged between 20-26 nm. The present system exhibits correlation length =1.6 nm and size of inhomogeneities = 3.2 nm. This clearly differentiates the micro-structural properties exhibited by various coacervate samples, which, in turn, is governed by the specificity of intermolecular binding mechanism. The structure and phase ordering kinetics in the coacervation of β-Lactoglobulin and acacia gum was investigated in details by Sanchez et al. [8,93]. Multiple growth processes during phase separation was observed in this system that was compatible both with late stage spinodal decomposition and nucleation and growth descriptions. In a related study [54], Sanchez and Renard showed that protein aggregates governed the complex coacervation between β-Lactoglobulin and acacia gum molecules, both by entropic and enthalpic effects. The results revealed that composite dispersions containing both protein aggregates embedded inside the complex coacervate and aggregate-free coacervates are formed simultaneously. The charge neutralization mechanism was clearly differentiated in their study. It was clearly shown that the intermolecular complexation between β-Lactoglobulin and acacia gum was mainly decided by neutralization of negative charges on acacia gum by positive charges of β-Lactoglobulin. In contrast during coacervation, the charge neutralization of complexes was achieved through lowering of acacia gum negative charges [8]. Weinbreck et al. [9,10,64,65,94] have studied the complex coacervation phenomenon in whey protein and gum arabic solutions and examined the composition and structure of the coacervate phase. The rheological studies revealed the viscous nature of their complex coacervate where G’’ dominated over G’. The viscosity of the coacervate was observed to increase with electrostatic interaction between the two biopolymers. The intermolecular complexes were visualized as gum arabic chains crosslinked by electrostatic interactions with whey protein molecules [9]. Thus, it appears that for each coacervation process there exists signature interaction, rheological behaviour and phase stability road map though some broad observables are common to all.
Agar, a polyanionic polysaccharide, was shown to undergo liquidliquid phase separation in presence of a polyampholyte, gelatin-B even though both the biopolymers had similar net charge. The interesting part was that it had no noticeable dependence on the ionic strength of the samples as far as the binding process was concerned. The titration and zeta-potential profile data supported this observation. The coacervation process started with the surface selective patch binding when both the molecules, agar and gelatin, had a majority of negative charge on them, followed by partial charge neutralization and aggregation of coacervate droplets. Since the agar molecule is stiffer than the gelatin molecule, the surface selective area (positive charge patch) of gelatin molecule binds over the agar rigid rod and partial charge neutralization takes place. On reaching the pI of gelatin, the gelatin molecule acquires more positive charge for the charge neutralization to proceed more aggressively. It was found that the salt-bridges helped in stabilizing the internal structure of coacervates. The charge neutralization gets initiated at pHC and reached its maximum at pHprep. Beyond this pH value, the potential gets contribution from the partially charge neutralized complexes and positively charged gelatin molecules. Regardless, the presence of salt ions was necessary to compensate for charge imbalance present in the soluble complexes and achieve charge neutralization (Table 5).
| Analysis | 1Gelatin [30, 62] | 2Gelatin-A: Gelatin-B [14] | 2Gelatin-A: Chitosan [11] | 2Gelatin-A: Agar [13, 63] | 2Gelatin-B: Agar [12] |
|---|---|---|---|---|---|
| Binding type | Electrostatic | Electrostatic | Surface selective | Electrostatic | Surface selective |
| Transition pH values | alcohol driven at constant pH | pHc ~ 5.5, pHF ~ 6.3 |
pHc ~ 4.5, pHF ~ 6.5-7.5 |
pHc ~ 5.4, pHF ~ 9 |
pHc ~ 7.5, pHF ~ 6 |
| Effect of Ionic strength | Yes | Yes | None | Yes | None |
| Optical nature | Opaque | Opaque | Opaque | Semi-transparent | Semi-transparent |
| Network structure | ζ = 20 nm, ξ= 1.2 nm |
--- | ζ= 21-26 nm, ξ= 1.2 nm |
ζ= 22 nm, ξ =1.2 nm |
ζ= 3.2 nm, ξ= 1.6 nm |
| Melting temperature | 33°C | 42°C | 64 °C, 87 °C | 35 °C, 75 °C | 75 °C |
| Viscoelastic property | Viscous | Viscoelastic | Viscous | Viscous | Viscoelastic |
Table 5: Comparison between various coacervates of agar and gelatin system. Reproduced with permission from American Chemical Society [12].
The microscopic structure can be imagined as the flexible gelatin chain binds to the stiff chain of agar at specific locations and the surface charge is influenced by the surrounding gelatin molecules. But the change in the thermo-mechanical properties must be attributed to the presence of both the gelatin and the agar molecules present inside the coacervate material. However, it will be appropriate to argue that the microscopic structure of the coacervate material comprised of weakly cross-linked polymer-rich zones separated by polymer-poor regions having characteristic viscoelastic length. Such systems are associated with two characteristic relaxation processes: one due to concentration fluctuation and another arising from viscoelastic relaxation. In summary, it has been unambiguously shown that surface selective binding promotes coacervation transition in the present system of biopolymers, though the electrostatic interactions are not screened by the presence of mobile ions. However, these ions create salt-bridges between the two biopolymers that enhance the thermo-mechanical characteristics of the complex coacervates formed. Surface selective binding is a poorly understood physical phenomenon and the present work intends to improve this understanding.
We acknowledge our collaborators B Mohanty, A N Gupta, S Boral, J Pathak, and A Tiwari. We are thankful to Dr. V. K. Aswal for assistance with SANS measurements.