Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2017) Volume 6, Issue 2
The paper presents the optimization method of turbine stages based on step-by-step application of onedimensional and three-dimensional optimization techniques of the main stage geometrical parameters. Using the developed method, the optimization of the 3rd stage of high pressure steam turbine K-540-23.5 was carried out. As a result of optimization a new stage with an absolute efficiency increase more than 1% compared to the original design was obtained. The reasons leading to such performance boost were analyzed and are represented in the paper.
<Keywords: Optimization method; Turbine stages; 1D and 3D Optimization; Mass flow rate; Inlet metal angle; Incidence angle
Symbols
A - Matrix of FMM coefficients
b - Blade chord
С - Velocity
F - Area
H0 - Isentropic heat drop
h - Specific enthalpy
l - Blade height
М - Mach number
Ns - Stage power
n - Independent factors number of FMM
P - Pressure
q - Vector of normalized varied parameters
Re - Reynolds number
r - Radius
S - Entropy
T - Temperature
t - Cascade pitch
u - Circumferential velocity
G - Mass flow rate
W - Relative velocity
Y - Formal metamodel (FMM)
αst, βst - Stagger angles of nozzle and blade cascades respectively
α - Outlet flow angle in absolute motion
m - Twist law coefficient
β - Outlet flow angle in relative motion
β1m - Blade inlet metal angle
β2m - Blade outlet metal angle
ξ - Losses
η - Efficiency
ρ - Density
φ, ψ - Velocity coefficients for nozzle and blade cascades respectively
Indices
0 - Stage inlet parameters
1 - Parameters in axial gap; nozzle wheel
2 - Stage outlet parameters; blade wheel
* - Total parameters
ij - Indices of the matrix
inc - Incidence
init - Initial, original
l - Leakage
opt1D - 1D optimization phase
opt3D - 3D optimization phase
u - Circumferential velocity component
z - Axial velocity component
The usage of computational fluid dynamics (CFD) in optimization algorithms makes it possible not only to solve the optimization task with high accuracy, but also to obtain a more detailed flow field in the turbine stage. However, the optimization using CFD requires significant computing resources that most often leads to the simplification of the problem statement and limiting the number of control parameters.
At the same time, optimization of the turbine stage using onedimensional or two-dimensional calculation methods demands significantly less time to perform the simulations. The disadvantage of using the methods of one-dimensional and two-dimensional theory for solving optimization tasks is a less detailed accounting of complex physical phenomena that take place in the turbine stage, as well as the usage of empirical dependencies for energy losses estimation, which reduces the accuracy and reliability of the obtained results.
To eliminate the mentioned above disadvantages, it is recommended to use a combined approach, for example, based on the use of onedimensional and three-dimensional theory to obtain the optimum design of turbine stages.
This paper presents the comprehensive results of development and further application of the combined method for optimization of the steam turbine stages.
To be confident that CFD simulation results corresponds to the real flow field during optimization process, the detailed verification of CFD simulations should be carried out firstly. Such study was performed previously; the results were presented at the 11th European Conference on Turbo machinery [1].
The turbine stage optimization problem is formulated and solved as the extremum search task:
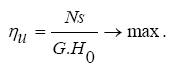 (1)
(1)
Wherein the accuracy of the obtained solution, as well as the level of computing resources needed for simulations, strongly depends on used optimization technique.
Proposed in this paper optimization technique on the stage of optimal solution search is based on replacement of the mathematical model, which describes physical phenomena and processes in the axial turbine flow path, to the approximation dependencies of the objective functions and functional constraints as a second-order polynomial (FMM):
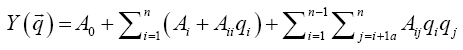 (2)
(2)
The dependency (2) is obtained in numerical experiment using the original mathematical models. It reflects only formal relation between the income and outcome parameters. Building the FMM for objective functions and functional constraints are carried out by Design of Experiment (DOE) methods Box-Behnken [2] and saturated Rechtschaffner plans [3].
For cases, where the FMM of the form (2) did not accurately represent the optimization problem (for example, in case of a multimodal objective function), we have proposed and used more advanced form of FMM (3), wherein the superposition of parabolas (the second term in dependency (2) is replaced by the superposition of cubic interpolation splines [4]. This change allows representing the complex functions with a high degree of accuracy.
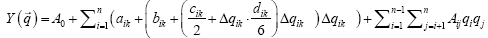 (3)
(3)
Where aik, bik, cik, dik – are the cubic spline coefficients of the current (kth) interpolation section and the ith independent variable. For each independent normalized variable qi there exist L interpolation areas in the range between -1 and +1; qik – is the distance between the current value of qi and the initial node coordinate of kth spline section for which coordinate qi is between the coordinates of its initial (kth) and final (k+1th) nodes; k = 1, 2, ..., L.
To find the optimal solution a pseudo-random Sobol’s sequence of numbers Sobol and Statnikov [5] is applied. The application of Sobol’s sequence is explained by the fact that it is well adjusted for solving the modern problems of optimal design in turbo-machinery: it makes minimal demands for the objective function smoothness; it is suitable for solving multi-objective functions within the functional and parametric constraints; it allows solving optimization tasks with a large number of control parameters.
At the one-dimensional (1D) optimization phase, to find the optimal values of control parameters, mathematical model of one-dimensional flow [6] is used. It consists of:
• Energy and continuity equations in the section behind the nozzle cascade:
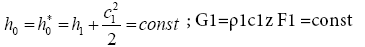 (4)
(4)
• Energy and continuity equations in the section behind the blade cascade:
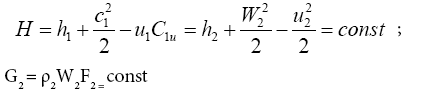 (5)
(5)
• Process equations in the sections behind the nozzle and the blade cascades:
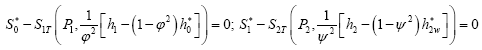 (6)
(6)
• Equation of state:
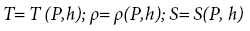 (7)
(7)
• Kinematic ratios linking the angles and the flow velocity in both absolute and relative motion;
• Closing ratios, linking parameters in the gaps (for example, a limit on the value of the stage heat drop).
The optimal values search at 1D optimization phase is performed with fixed mass flow and providing zero incidence angle on the blade cascade (β1 = β1m). Herewith, inlet and outlet boundary conditions, as well as mass flow, correspond to predetermined values or to data obtained from the CFD simulation of the original turbine stage. The flow parameters from hub to shroud are distributed in accordance with the twist law Сur = const.
At the three-dimensional (3D) optimization phase CFD simulations, based on the Reynolds-averaged Navier-Stokes (RANS) equations, are carried out. The k-ω SST turbulence model is used for all simulations. Meshing is performed with accordance to the recommended values of the y+ parameter for the specified turbulence model.
The control parameters are: for one-dimensional optimization – outlet flow angles α1, β2 and relative pitches (t/b)1, (t/b)2; for threedimensional optimization – twist law coefficients m1, m2 (8) and correction of the blade inlet metal angle Δβ1m.
For the twist law variations the following dependencies are used:
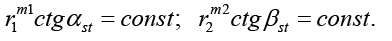 (8)
(8)
Parameters m1 and m2 characterize the stagger angle changing: when m > 0 stager angle is increasing from hub to shroud, when m < 0 stagger angle is decreasing [7].
Developed optimization algorithm is presented in Figure 1. In the first stage of the algorithm three-dimensional CFD simulation of the original turbine stage is carried out. It is the starting point of the optimization. Next one-dimensional optimization is performed. The new turbine stage is designed and is simulated using CFD. Obtained in the simulation mass flow G is compared to the mass flow G0 of the original stage. If they do not match, then you return to onedimensional optimization phase, specify the new mass flow and repeat the 1D optimization. This cycle is performed until the mass flow in CFD simulations of the new optimized turbine stage is equal to the mass flow G0 of the original turbine stage. Typically, such matching can be achieved in three iterations.
The next algorithm phase is a three-dimensional optimization using CFD. Corresponding to the established DOE plan, CFD simulations of different turbine stage designs are performed. According to the simulation results FMM of the form (3) for stage efficiency is obtained. When extremum is found, the new turbine stage is designed based on appropriate optimal control parameters. For this new optimal turbine stage CFD simulation is performed. Next, the accuracy of resulting formal metamodel is verified: the values of objective function (stage efficiency) calculated by FMM and simulated in CFD are compared. If their difference is greater than 0.05 % the range of control parameters variation should be narrowed with repeating of the 3D optimization. Otherwise, the optimization task is considered to be solved.
It is need to be noted that optimization algorithm do not have fixed set of control parameters. They can be changed depending on the optimization problem formulation – user should pick them manually. It is recommended to choose for 3D optimization parameters the impact of which can be correctly evaluated only in 3D CFD simulations (twist laws, leans etc.). All other parameters should be used in 1D optimization to achieve the most effective result in the shortest possible time.
To confirm the efficiency of the developed optimization method the optimization of 3rd stage of high pressure steam turbine K-540-23.5 has been carried out (Figure 2).
Boundary conditions are P0* = 13397.6 kPa, h0* = 3198.734 kJ/kg, P2 = 11604 kPa. Such boundary conditions provide a subsonic flow in the entire stage (the Mach number does not exceed M = 0.475). The steam mass flow in the turbine is G = 432.42 kg/sec, Reynolds number at the mean radius Rec1 = 4.7*104. The main geometrical characteristics of the stage can be seen in Table 1.
| Parameter | Nozzle | Blade |
|---|---|---|
| Outlet flow angle (α, β) | 11.63° | 18.31° |
| Relative cascade pitch (t/b) | 0.381 | 0.708 |
| Relative length (l/b) | 0.489 | 1.099 |
| Rotor speed (N) | 3000 rpm |
Table 1: Main geometrical characteristics of the original stage.
Mesh model of the turbine stage shown in Figure 3 was built to carry out the CFD simulations. The computational model consists of three domains: the Nozzle domain; the Blade domain; and the domain, combining the axial gap, the radial gap and the exhaust pipe (Clearance domain).
The nozzle mesh has 180 × 98 × 90 elements while the blade mesh has 125 × 98 × 90 elements. The Clearance domain was computed from the tetrahedral elements with thickening in the areas where the flow parameters may be significantly changed and with prismatic boundary layer. The number of elements in the Clearance domain is equal to 7.3 million. Thus, the total number of elements in the computed mesh exceeds the value of 10 million, which is a prerequisite to obtain the accurate results. Moreover, on each solid surface the computed mesh has the thickening to ensure the value of the y+ parameter is less than one. Special attention was paid to the mesh in the radial gap. The flow here has a complex spatial nature, therefore, the maximum size of mesh elements in this area has been noticeably reduced (Figure 4).
After 1D optimization phase the efficiency of the turbine stage was increased by 0.587%, after 3D optimization phase additional efficiency increasing of 0.421% was obtained (overall efficiency rise is 1.008%). Optimal selection of the (t/b)1 parameter during 1D optimization has reduced the friction surface and the portion of the edge wake in the flow, which decreased losses in the nozzle cascade. At the same time the value of (t/b)2 parameter in the original stage was already optimal.
As it was planned in the optimization algorithm, after 1D optimization phase a zero incidence angle was obtained on the mean radius of the blade cascade (Table 2, Figures 5 and 6). Thereby, the blade profile losses were decreased (Table 2). However, since the stagger angle of the blade remains constant along the radius, the considerable unevenness of incidence angle was retained, which in turn led to offdesign incidence angles at hub and shroud of the blade (Figures 5 and 7). Furthermore, it is known that zero incidence angle is not always the best choice in terms of profile losses decreasing [8,9].
| Parameter | Original | 1D | 3D |
|---|---|---|---|
| stage | optimization | optimization | |
| Efficiency, % | 88.236 | 88.823 | 89.244 |
| Degree of reaction | 14.264 | 22.896 | 21.803 |
| Mass flow (G), kg/s | 432.525 | 431.373 | 432.976 |
| Leakage (Gl/G), % | 1.219 | 1.426 | 1.39163 |
| ξ nozzle, % | 3.591 | 2.766 | 2.748 |
| ξ blade, % | 6.463 | 5.922 | 5.386 |
| ξ exit energy, % | 3.045 | 2.947 | 2.983 |
| (t/b)11 | 0.38 | 0.501 | 0.501 |
| (t/b)2 | 0.708 | 0.708 | 0.708 |
| α1, degree | 11.63 | 12.258 | 12.258 |
| β2, degree | 18.31 | 16.63 | 16.63 |
| β1m, degree | 32.814 | 28.973 | 38.144 |
| Incidence angle, | 6.287 | -0.074 | 9.655 |
| degree |
Table 2: 3D simulation results of original and two optimized stages.
The problem of determining the optimal geometric incidence angle has been resolved at the 3D optimization phase.
Previously was mentioned that the 3D optimization phase has improved the absolute stage efficiency by 0.421%. The difference between the results calculated by FMM and simulated in CFD was 2.5*10-4. The main reason of the performance boots is the losses reduction in the blade cascade (Table 2). Obviously, such boost became possible due to the optimal choice of the inlet metal angle β1g and the blade twist law. The application of twist laws to nozzle and blade cascades significantly changed the outlet flow angle from the nozzles and the relative inlet angle of the flow on the blades (Figures 5 and 6). In 3D optimized version, the inlet angle of the flow on the blades β1 is aligned along the height. This distribution secured uniform flow on the rotor blade over the entire height with the optimal value of inlet metal angle. The incidence angle equal to 9.5° (Figure 7). This has led to a more favourable nature of the flow around the blades and significantly decreased the profile losses in whole cascade (Table 2).
Detailed examination of the flow in the turbine stage shows that the blade profile obtained considering zero incidence angle (1D optimization phase) has the local velocity acceleration on the suction side close to the leading edge with its subsequent inhibition (Figures 8 and 9). Reducing of the flow velocity inside the blade cascade indicates to a presence of the local diffuser region therein. This conclusion can also be confirmed considering the chart of velocity distribution around the blade profile at mean radius after 1D and 3D optimization phases (Figure 8, Areas 1 and 2). Distribution was obtained at a normal distance of 1 mm from the blade surface to ensure that the influence of boundary layer on the flow is eliminated.
Obviously, such flow is not optimal in terms of the minimal profile losses.
After 3D optimization phase the blade inlet metal angle β1m was changed, which decreased the blade curvature and increased the geometric convergent degree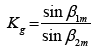 of the flow path (Figures 9 and 10). This resulted to elimination of diffuser regions in the channel and, therefore, significantly improved velocity distribution of the flow around the blade profile (Figure 8).
of the flow path (Figures 9 and 10). This resulted to elimination of diffuser regions in the channel and, therefore, significantly improved velocity distribution of the flow around the blade profile (Figure 8).
The value of the reaction degree and its gradient after 3D optimization decreased a bit, which led to a slight reduction of the leakages through the radial gap (Table 2).
The research work shows that the developed optimization method, which combines one-dimensional and three-dimensional optimization phases, is a powerful tool for significant efficiency improvement of the turbine stages.
Using the developed method, the optimization of the 3rd stage of high pressure steam turbine K-540-23.5 was carried out. As a result of optimization a new stage with an absolute efficiency increase more than 1% compared to the original design was obtained.
The detailed analysis of the reasons leading to such performance boost has shown that stage efficiency is increased due to:
1. Selection at the mean radius the optimal values of α1, β2, (hence the values of degree of reaction) and relative cascade pitches (t/b)1 and (t/b)2, which reduces nozzle, blade losses and exit energy losses;
2. Selection of the optimal value of the blade inlet metal angle β1m, which provides enhanced geometric convergent degree of the channel and lead to the elimination of local diffuser regions in it, improving the flow around blade profile;
3. Obtaining of the optimal twist law, which provide a uniform flow on the rotor blade over the entire height.
Authors express gratitude to Director of Engineering Institute Prof. S.I. Serbin for the kindly offered possibility of carrying out CFD simulations with usage of ANSYS CFX in National Shipping University named after Makarov.