Transcription is vital for normal functioning of all organisms, as it is the most significant regulation level of gene expression. An interest in detailed analysis of transcriptional regulation grows due to new large-scale data acquisition techniques. There is a large amount of experimental data available about the Drosophila segment determination system. The gap gene system implements the most upstream regulatory layer of the segmentation gene network. It receives inputs from long-range protein gradients encoded by maternal coordinate genes and establishes discrete territories of gene expression. In this process the gap gene cross-regulation plays important role. The formation of gap gene expression domains is a dynamic process: the domains do not form in one place, but instead in the posterior half of the embryo they shift anteriorly during cleavage cycle 14. Despite our expanding knowledge of the biochemistry of gene regulation, we lack a quantitative understanding of this process at a molecular level.

We applied the systems-level approach to study gap gene network in Drosophila. A combined sequence-based model of gap gene regulatory network controlling segment determination in the early Drosophila embryo was developed. We modified the recent model from [1] in three ways. First, we narrowed down the spatial domain of the model by considering only the trunk region of blastoderm from 35% to 92% of embryo length along the A-P axis. This allowed us to combine the data on protein concentration from FlyEx database [2] and on mRNA concentration from SuperFly database [3] in the fitting procedure. Second, we used the same BTM parameter and the same range for short range repression for all targets and TFs. Third, we allowed several activator molecules to contact BTM simultaneously.

The state variables of the model are the concentrations of mRNAs and proteins encoded by four gap genes hb, Kr, gt, and kni. The binding sites for 8 TF – the products of hb, Kr, gt, kni, bcd, tll, cad, and hkb genes in the potential regulatory region from 12Kbp upstream to 6Kbp downstream of TSS for each gene were predicted in [1] according to [4]. We modified thermodynamic approach originally proposed in [5]. The target gene expression at mRNA level is proportional to the promoter occupancy that is determined by the concentration of TFs. The dynamics mRNA and protein concentrations is described by the system of differential equations with the delay parameter that accounts for the average time between events of transcription initiation and corresponding protein synthesis.

The promoter occupancy of every target gene for every embryo nucleus at every point of time was calculated in the form:

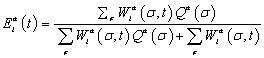(1)

where σ is a molecular configuration of the regulatory region for gene a, 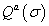is the Statistical weight of the interaction between TFs and bound basal transcriptional machinery (BTM), and 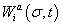is the statistical weight of configuration σ for nucleus-time coordinate (i,t), that depends on the concentration 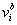of all TFs regulating gene a in nucleus i at time moment t. The system of differential equations considers both mRNA and protein synthesis. The equation for mRNA concentration 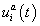of target gene a in nucleus i included Production, diffusion and decay terms. The equation for protein concentration 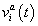described protein synthesis, diffusion and degradation.

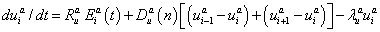(2)

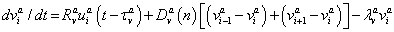(3)

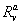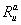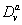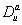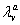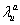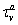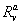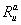where n is the cleavage cycle number, and are maximum synthesis rates, , are the diffusion coefficients, and and are decay rates for protein and mRNA of gene a. The parameter is the delay parameter. Where n is the cleavage cycle number, and are maximum synthesis rates, 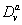, 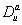are the diffusion coefficients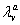, and and 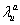are are decay rates for protein and mRNA of gene a. The parameter 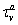is the delay parameter.

Model fitting was carried out by differential evolution (DEEP) method [6] to minimize the combined objective function. This function is a sum of the residual sum of squared differences between the model output and data, weighted pattern generating potential and a penalty term, which limits a growth of regulatory weights. The weighted pattern generating potential was proposed in [7] to account not only for the magnitude of difference between model and data, but also for the direction of change.

Concentration profiles for mRNA and protein for 4 target genes–hb, Kr, gt and kni are presented in Figure 1 together with experimental observations from FlyEx and SuperFly used for fitting.

Figure 1: Model output for a representative network as compared to protein concentration profiles from the FlyEx database (upper row) and mRNA concentration profiles from the SuperFly database (bottom row). Results are shown for time class 6 in cleavage cycle 14A.