Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
+44-77-2385-9429
ISSN: 2168-9792
+44-77-2385-9429
Research Article - (2018) Volume 7, Issue 1
A computational study is conducted to investigate the aerodynamic performance of a newly designed corrugated airfoil of dragonfly at range of low Reynolds number 15000-38000. This study represents the transient nature of corrugated airfoils at low Reynolds number where flow is assumed to be laminar, unsteady, incompressible and two dimensional. This research comprises of the investigation of the aerodynamic performance of various corrugation configurations at different corrugated angle (i.e., 4°, 8°, 12°) with varying pitch length and peak height along the span wise and chordwise directions. The 12° corrugated angle is incorporated in the new modified design with varying pitch length, corrugated angle and peak height to achieve the higher lift to drag ratio. The simulation is carried out using Ansys CFD as a simulation tool and ICEM CFD as a modeling tool for 2-D corrugated airfoil. The design features of corrugated airfoil used in this research is not used in earlier studies. The simulation includes a sharp interface cartesian grid-based meshing and k-ε model for turbulence model. The computational results show that the newly designed corrugated aero foil generates more lift and less drag compared to flat plate and NACA 0015 aero foil and also helps in preventing large scale flow separation.
<Keywords: 2-D corrugated aero foil; Dragonfly; Low Reynolds number; Ansys CFX/Fluent; Flat plate; NACA 0015
Among natural flyers, dragonflies have unique features and flight capabilities. Their flight performance far exceeds many other flying insect species. The complex morphology of the dragonfly wing cross section (airfoil) is very different from the traditional closed, thick and smooth airfoils of low Reynolds number airplane. Okama et al. [1] isolated the influence of different geometrical parameters and showed that the surface texture or the roughness of wings results in an increased maximum lift coefficient, CLmax and increases maximum lift to drag ratio (L/D)max. Dragonfly wings are highly corrugated, which increases the stiffness and strength of the wing significantly and results in a lightweight structure with good aerodynamic performance. Corrugation provokes an early transition to turbulent flow over the two-dimensional airfoil, permitting reattachment of the flow over the wing called laminar bubble.
Dragonfly being a natural flyer the vein and the membrane structure are flexible in nature as shown in Figure 1 Therefore; it will be difficult to predict the behavior of corrugated wing during flight condition. It has a flapping frequency between 30 Hz and 50 Hz. Flapping flights of dragonflies has been extensively studied by Savage et al., Alexander [2], Wakeling and Ellington. According to Rees [3] the fluid flowing over the airfoil gets trapped in the corrugation valleys where it either becomes stagnant or rotates slowly, resulting in virtual profiling over the corrugated airfoil.
Kesel [4] noticed trapped vortices present in the folds that serve to change the effective profile of the airfoil. With the advent of bio-inspired aerial vehicle, it has become clear that there is much that can be learnt from insect flight that could be translated into engineered systems. At a higher Reynolds number, it is hypothesized that the dragonfly actually flies without wing flapping [5]. The negative pressure developed in these corrugations contributes to the excessive lift. It is the reason that makes further investigation into the aerodynamic aspect of dragonfly wing worthwhile. This study focuses on the aerodynamic characteristics of the newly modified corrugated design and the flow pattern around a dragonfly corrugated wing of a particular cross-section (Figure 1).
Geometry selection and design
Three types of the airfoils are used in the present study i.e., triangular wave modeling at different corrugation angles (i.e., 4°, 8° and 12°) and varying pitch length, Modified wing 1(MW-1) and Modified wing 2(MW-2). The dragonfly airfoil used in the present study is cambered and has the chord length of 110 mm, peak height 2 mm and thickness of wing is 2 mm [6-9].
Computational domain: After modeling the wings in CATIA, it is exported to ANSYS 15(FLUENT) and the analysis of the aerodynamic performance of corrugated aerofoil is carried out by using structured grid Navier-stokes equation. Grid points are denser near the airfoil wall region to capture flow characteristics accurately [7,8].
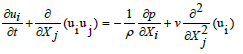
Boundary conditions
The flow around the corrugated airfoil is assumed to be laminar, incompressible, unsteady and 2-dimensional. The outlet of the domain was set to pressure outlet where the value of the gauge pressure is set to zero (Table 1).
| Dynamic viscosity (m) | 1.7895 × 10-5 Ns/m |
| Density | 1.23 Kg/m3 |
| Inflow velocity (U∞) | 2.067 m/s |
| Reynolds number | 15000 |
Table 1: Boundary conditions.
From the analysis, we observed that as the corrugation angle increases, the flow separation delays and the also the velocity increases which gives a better lift to drag ratio than the lower corrugation angles. Out of these 12° corrugation angle performed much better giving high L/D ratio compared to others (Figures 2-5).
Figure 4: The instantaneous flow field at α= 0° (a) pressure plot for 4° corrugation angle (b) velocity plot for 4°corrugation angle (c) pressure plot for 8° corrugation angle (d) velocity plot for 8° corrugation angle (e) pressure plot for 12° corrugation angle (f) velocity plot for 12° corrugation angle.
Based on this analysis, 12° corrugation angle is incorporated in the new design with increasing angles of corrugation with a curved profile near the trailing edge region which helps in delaying the flow separation and also reduces vortices, hence reducing drag (Tables 2 and 3).
| Type of wings | Angle of attack (degree) |  Ratio Ratio |
|---|---|---|
| 4° Corrugation angle | 0° | 0.7731 |
| 8° Corrugation angle | 0° | 1.468 |
| 12° Corrugation angle | 0° | 1.9 |
Table 2: Variation of L/D ratio for different corrugation.
| Type of wings | Angle of attack | CL | CD |  Ratio Ratio |
|---|---|---|---|---|
| MW-I | 0° | 3.0987 | 0.95442 | 3.25 |
| MW-II | 0° | 3.108 | 1.14878 | 3.108 |
| Flat plate | 0° | 0 | 0 | 3.12 |
| NACA 0015 | 0° | 0.016065 | 0.55803 | 0.028 |
Table 3: Result comparison.
Design and analysis of modified wing
Now taking above design in consideration the corrugated design is modified with increasing corrugation angles in ascending and descending order (i.e., 12°, 36° and 48°) and vice versa with increasing peak heights and having a curved profile at the trailing edge as shown in Figures 5(a) and 5(b).
Analysis of modified wing-I (MW-I) and analysis of modified wing-II (MW-II)
In this it is clearly observed that as the highest corrugation angle is at the beginning of the wing, the flow is getting separated at the first peak itself and flow is reattaching at the end of the wing (Figures 6-8).
Figure 6: The instantaneous flow field at α = 0° for MW-I (a) Velocity distribution(b) Velocity contour (c) Velocity pathline (d) Turbulence contour (e) Pressure distribution As we can observe, the velocity is high at the peaks of the corrugations and at the valleys the velocity is zero indicating reversed flow or vortices formation as shown in Figure 6 (a). The flow velocity is trapped into the valleys of modified wing-I as shown in Figure 6 (c) which helps in delaying separation and flow will stick to the surface. The pressure distribution shows high pressure at the stagnation points and lowest pressure at peaks and at the valleys there is low pressure indicating reversed flow as shown in Figure 6 (e). Analysis of modified wing-II (MW-II).
Comparisons of modified corrugated wings with flat plate and NACA 0015
The comparative observations made through Figures 8(a)-8(d), have been represented in Table 3.
A computational simulation on dragonfly corrugated wing cross section is performed at Reynolds numbers between 15000 and 38000. The results of the corrugated airfoils are compared with flat plate and NACA 0015 airfoil. We observed that the vortices formed on the corrugated aerofoil and shed into its wakes produces lower integral force fluctuation because of the its upstream peak height which allows the flow to reattach near the trailing edge of the airfoil by delaying flow separation [10-12]. The aerodynamic performance i.e., (L/D) ratio of the modified wing –I (MW-I) is better compared to MW-II and NACA 0015 at 0° angle of attack. It is found that the design criteria being used, and simulation carried out on MW-I and MW-II is giving much better result as compared to that of earlier studies. For MW-I as the angle of attack increases L/D ratio increases as the flow remains attached to the surface and get trapped into the valley, hence the performance of our design is much better than compared to earlier studies being conducted on the aerodynamic behavior of the corrugated dragonfly airfoil.