Ultra short extreme ultraviolet (XUV) pulses produced by highorder harmonic generation (HHG) from atoms or molecules opens up a new era for time-resolved studies of ultrafast dynamics in atomic [1,2] and molecular systems [3-5], and in solid state [6-8] and plasma physics [9,10]. Since the HHG spectrum depends on the structure of the atom or molecule a new method for the tomography of atomic and molecular structures has been proposed and developed [11,12].

For high output of the harmonic intensity a long interaction length is necessary but it is not easy to maintain the phase-matched propagation of the fundamental and harmonic radiation. The coherent construction of the harmonic field in the macroscopic medium or so-called phase-matched generation is reflected in the temporal and spatial profile of the harmonic intensity and plays a major role in experimental aspects. Because of the optical properties of materials in the XUV range the medium for HHG is usually a gas. The degree of phase-matching depends on the harmonic order and a number of experimental parameters including the atomic and molecular dispersion, the absorption coefficient of the target gas at the harmonic frequencies, the ionization fraction, and the gradient of the driving laser field. These dependences are not well understood.

The generation of phase-matched high-harmonic radiation in the near cut-off region can be obtained by using a moveable focusing lens in a semi-infinitive gas cell [13]. The effect of the neutral gas dispersion on the pump beam, the plasma dispersion due to ionization and the phase change along the focusing beam can be balanced under certain conditions. Phase-matching high harmonic generation at very high photon energy is difficult because a strong driving field is required that creates a large free-electron dispersion through strong ionization of the gas. Three important effects result from ionization of the medium: the depletion of the medium, plasma dispersion due to the free electrons, and defocusing of the laser beam by the radial distribution of the electrons. For an 800 nm driving laser, the “critical” ionization levels above which true phase matching is not possible are ~3.8% for argon and ~ 0.5% for helium; thus efficient phase-matched HHG has been demonstrated only at photon energies < 50 ev for argon and < 100 ev for helium [13,14]. The cut-off rule for the generated harmonic photon energy is hv_max=I_p+3.2Up, where I_p is the ionization potential of the gas and U_p is the ponder motive energy given by U_p~I_Lλ_L², and I_L and λ_L are the intensity and wavelength of the driving laser. The λ_L² scaling of the cut-off shows the advantage of using long wavelength driving pulse to generate higher harmonic orders. However the higher pressures of gas required for HHG using infrared (IR) wavelengths to overcome the low efficiency would be difficult to obtain in a free-space gas jet configuration.

The mixing of two or more laser pulses with the same or different wavelengths can be used for the generation of continuous XUV spectra [15,16]. A combination of a polarization and a two-colour grating gives rise to a new kind of technique named double optical gating [17] for the isolation of a single at to second pulse. When the frequencies of two laser fields are incommensurate the total electric field is significantly different from a simple sinusoidal field and then the electron trajectories are strongly dependent on the given optical cycle. The superposition of two co-polarized fields of different frequency can be considered and are pea table short time window still occurs, although it cannot be ascribed to a change in the polarization. The HHG suppression can be seen as a consequence of the deviation of the driving field from a pure sinusoidal field.

Molecules and especially linear diatomic molecules such as N₂ or O₂ are not isotropic systems. When the molecules are aligned the HHG is influenced by the angle between the molecular frame and the polarization vector of the femtosecond laser field [18]. Field-free aligned molecules can be prepared by the interaction of molecules with a short, relatively weak pulse to create a rotational wave packet. A superposition of the dephased wave packet after the aligned pulse is created at intervals separated by their fundamental rotational period leads to a periodic alignment of the molecules. Because the ionization and dispersion are dependent on the alignment of the molecules the HHG intensity for different magnitudes and angles of alignment can be detected and used to study the rotational molecular dynamics [12,19].

In this paper we report the use of a second beam to vary the phasematching condition and driving field in the HHG process in a semi-infinitive gas cell. We demonstrate that the phase matching can be enhanced or destroyed by the second laser beam. The enhancement of the phase-matching at high ionization rate with the second beam can be used to increase the cut-off photon energy. A second beam with a different carrier frequency can be used for generation of continuous XUV spectra. In a molecular gas the second beam creates a rotational wave packet which leads to a modulation of the HHG intensity at the rotational period.

Phase matching in high harmonic generation

When atoms or molecules interact with an intense laser field a high-order nonlinear polarization is induced which acts as a source for the generation of a high-order harmonic field. The electric field of the q^th harmonic over the length of interaction l along the propagation direction of the fundamental field is given by

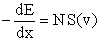(1)

where l_med is the total medium length, l_abs is the absorption length, d_q (I,z) is the amplitude of the high-harmonic dipole, Δk_q (I,z) is the phase mismatch between the harmonic radiation and the laser induced polarization, c and ε are the speed of light and vacuum permittivity, ω is the angular frequency of the laser pulse and I is the laser intensity. The integration is over the length of the interaction medium and the intensity envelope of the driving laser.

The amplitude of the high-harmonic dipole d_q is dependent on the intensity of the driving laser field with peak intensity I₀, which varies along the focus (z) direction and perpendicular to the z direction (r) across the beam profile, and is also dependent on the properties of the gas medium such as the ionization energy and the orientation of the atoms or molecules relative to the driving field. In the single-atom response model d_q scales as (1-η) I_L⁶ [20] in the intensity window of the driving pulse I to I+dI.

The phase mismatch Δk along the axis of the fundamental laser beam can be expressed as

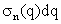(2)

Where q is the harmonic order, k is the phase velocity, λ is the laser wavelength; P, η and r_e are the gas pressure, ionization fraction and classical electron radius, respectively; N_e is the density of the free electrons, δn = n_laser – n_q is the difference in the refractive indices of refraction of the gas at the fundamental and harmonic wavelengths.

The geometric term of the phase mismatch depends on the geometrical configuration such as the Gouy phase associated with focusing of a Gaussian laser beam. The dipole phase mismatch term is the phase of the atomic or molecular dipole. The origin of this phase is the action acquired by the electron leading to the emission of the q^th harmonic in the continuum state.

The free electron density which depends on the radial distribution of the laser intensity leads to a radial variation of the dispersion that is equivalent to a divergent lens. Thus the effective intensity reached in the medium is lowered and the atomic dipole and the geometrical phase gradient in the medium are modified. The dependence of the laser field on the propagation clearly shows that the dipole phases cannot be established assuming an unperturbed laser beam. In a semiinfinite gas cell the dipole phase cannot be neglected and the phase gradient of the dipole phase allows the phase mismatch to be reduced on-axis where the laser intensity is high. This leads to an enhancement of the efficiency because the atomic response is high in this region.

The atomic phase gradient acts as an additional time dependent wave vector that allows the high plasma dispersion to be compensated.

Because the free electron plasma dispersion depends on the ionization rate, phase- matching is possible only for ionization levels η below a critical level of ionization given by Brichta et al. [21].

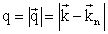(3)

The critical ionization level is low (< 3% for Ar and <1% for He gas) and the cut-off of the phase-matched HHG is always lower than when a single-atom response is considered. The ionization rate is dependent on the laser intensity and pulse duration and also on the orientation of the atom and molecular dipole to the laser field. To generate very high harmonic orders high laser intensity is required which leads to ionization levels that are greater than the critical ionization and the harmonic intensity then becomes very low due to the large phase mismatch.

The interaction of a high-intensity femtosecond pulse with atoms or molecules produces a nonlinear refractive index in the medium. The change in total nonlinear refractive index Δn_total (λ,t) consists of instantaneous and non-instantaneous contributions

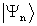(4)

The instantaneous contribution gives rise to an instantaneous nonlinearity in which the magnitude directly follows the intensity profile of the fundamental laser field.

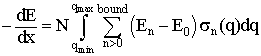(5)

Where n₂ (λ) is the nonlinear refractive index due to the bound electrons of the atoms and molecules and I (t) is the laser intensity. The delay of the atomic or molecular response to the field, e.g., due to dephasing and/or rotational Raman, leads to a non-instantaneous change Δn_noninstant(λ,t) in the refractive index which can be observed after the laser pulse is finished.

A 1 kHz multi-stage, multi-pass, chirped-pulse amplifier system which produces up to10 mJ pulses with a duration of 30 fs and centered at 800 nm is used for our experiment. To obtain an infrared pulse at 1400nm, 800 nm pulses are used for pumping an optical parametric amplifier (OPA) system which consists of three stages. A collinear OPA scheme is used in order to efficiently amplify the infrared signals. Type II bismuth triborate (BIBO) nonlinear crystals, cut at θ =42° in the x-z principal plane (φ =0) for o → eo interaction, are used in all subsequent stages. The advantages of using type-II interaction are related to the ability to tune, even close to degeneracy, at almost constant bandwidth for the signal and idler. The total conversion efficiency for this OPA is >40%, producing a maximum output of ~ 2 mJ at 1400 nm. For setting two beams with different wavelength only 6 mJ of the 800 nm pulse is used to pump the OPA. Details of the HHG setup and detection system have been published elsewhere [13,22].

When only an 800 nm laser pulse is used the laser beam is split into two beams with an intensity ratio of first beam to second beam of about 4:1. The polarization of the second beam relative to that of the first beam can be changed using a half-wave plate. The two laser beams are focused to a single spot in a gas-filled cell at an angle of about 5o. When a 1400 nm laser pulse is used as the first (driving) pulse for HHG the second pulse at 800 nm can be aligned in a co-propagating direction with a dichroic mirror. The first beam drills an exit pinhole in a thin Al plate allowing straightforward handling and no further alignment procedures along the optical axis. The diameter of the two beams at the focus is ~100 μm and the length of the overlapping area is ~ 500 μm which can be varied by changing the size or focus position of the second beam. Positive time delay implies that the second beam precedes the first beam. When the intensity of the first beam is >6×1014 W/cm² the enhancement of the ionization and Rayleigh scattering from free electrons in the region where the two pulses overlap can be used for spatial and temporal alignment of the pulses.

Atomic and molecular gases with different ionization energies, such as helium (23.59 eV), argon (15.76 eV), nitrogen (15.58 eV) and oxygen (12.03 eV), are used in this study. The electron configuration of the ground state has σ - symmetry in the case of N₂ and π-symmetry in the case of O₂.

Phase-matched generation of the high-order harmonics

Using a 300 mm focal-length lens the radius of the focused intensity distribution of the femtosecond laser beam varies from approximately 45 to 100 μm and the Rayleigh range varies from 20 to 5 mm for an aperture with diameter ranging from 5 to 10 mm. Allowing for defocusing due to the generated plasma, the effective focused peak intensity ranges from to 3×10¹⁴ W/cm². The pressure, aperture diameter, energy and chirp of the first laser pulses are optimized for maximum flux for all available harmonics. At a fixed pressure and position of the focus the optimization of the harmonic beam by means of a variable-diameter aperture applied to the first laser beam is mainly due to the effective f-number, the beam quality of the laser beam, the complex interplay between the intrinsic phase of the harmonic emission and the laser phase [23] and the change of ionization rate. The good beam quality in the harmonic far field and the small bandwidth of the harmonic spectrum indicate that phase-matching is mainly satisfied along the propagation axis of the pump pulse [13]. Off-axis radiation is also generated in the near field, but the harmonic radiation generated under phase-matched conditions has low divergence properties.

The inset in Figure 1 shows the HHG spectrum for argon gas at a pressure of 60 Torr. The wavelength of the driving pulse is 800 nm. Two laser intensities, a low intensity (0.6 mJ - dashedline) and a high intensity (2.2 mJ – full line), are used for optimization of the HHG intensity and profile before the laser intensity is set to 2 mJ. When high laser intensity is used for optimization the ionization rate is kept below a critical ionization rate over the full range of available intensity. The phase mismatch is a minimum for a short quantum path and hence a high photon energy is generated and the spectrum exhibits narrow harmonics (full line in the inset of Figure 1). When a low intensity is used for optimization and a high laser intensity is applied later the phase mismatch is large and a longer quantum pathway must be considered for the harmonic generation process,and hence the harmonic spectrum is broad (dashed line in the inset of Figure 1). The output intensity of harmonic 23 (H23) versus intensity of the driving laser is displayed in Figure 1 for two cases of optimization. When the high laser intensity is used for optimization the HHG intensity scales as I₀₆ where I₀ is the peak intensity of the laser at low laser intensity (< 1mJ). At low laser intensity the ionization rate and phase mismatch are very small and only a few cycles around the peak intensity contribute to the HHG. The dependence of the HHG intensity on the intensity of the laser pulse at high laser intensity (>1 mJ) can be fitted with the equation

Figure 1: Intensity of harmonic 23 (H23) from argon gas versus intensity of the driving laser for two optimized cases of the driving laser intensity a) 0.6 mJ (triangles) and b) 2.2 mJ (circles). The symbols show the experimental data and the lines show the fit. The inset shows the HHG spectrum for two optimized cases when a 2 mJ laser pulse is applied.

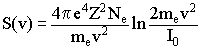
Where Δkq (I₀)=A+BI₀, and I₀ is the laser peak intensity. This dependence shows that in this intensity range the dipole moment remains unchanged while the phase mismatch increases linearly with laser intensity. The linear dependence of the phase mismatch on laser intensity reflects the fact that the dipole phase term plays an important role. When low laser intensity is used for optimization the phase mismatch is larger and the variation of the phase mismatch is more complicated because the plasma dispersion is high.

The phase-matched generation can also be obtained for the case of a 1400 nm driving pulse. When the focal point position is setting at the exit pinhole (z=0) Figure 2 show the dependence of the total intensity on pressure for 105^th (H 105) and 71^st (H71) harmonics. The optimized value for the pressure is found to be p_Ar=370 Torr. For p_Ar <370 Torr the harmonic intensity increases quadratically with pressure (p²) and thus indicates that the harmonic emission is phase-matched for this spectral band width. For p_Ar > 450 Torr the variation of the harmonic emission intensity is dominated by re-absorption of the generating gas and an exponential decay curve can be fitted in this region (Figure 2). Also, larger values of pressure appear to optimize the phase-matching conditions for higher harmonic orders and allow a larger number of atoms to contribute to the coherent build-up of a higher harmonic order.

Figure 2: Intensity of 105^th (H105) and 71^st (H71) harmonics from argon gas versus the gas pressure when a pulse at 1400 nm is used for HHG. P² scale indicates that the generation of harmonics is phase-matched.

Instantaneous response to the second field

Two laser fields with same wavelength: When the second laser field is applied and overlaps in time with the first field an additional mismatch factor in the overlapping region is created which influences the total phase-matched condition. The minimum of the phase mismatch established by optimization of the first laser field is disrupted, i.e., the harmonic intensity is decreased. The variation of the intensity of H25 from argon gas versus the delay time of the two beams is shown in Figure 3a for an intensity of the second pulse ~ 10¹³ W/cm². A similar dependence is observed for other harmonics ranging from H17 to H27 and also for harmonic spectrum from helium. When the polarizations of the two laser fields are parallel the harmonic intensity is very low around zero delay time and when the polarizations of two fields are crossed the change of harmonic intensity is small. Since the ionization rate of the atomic medium in the overlapping region under the influence of the second pulse should be independent of the polarization the change of phase mismatch will be caused by the dipole phase or the nonlinear refraction index. The origin of the dipole phase is the action acquired by the electron leading to the emission of the harmonic in the continuum state. The interaction of the second field with the free electrons influences the trajectory and re-scattering of the electron causes large change in the dipole phase. When a more intense second field (~3×10¹³w/cm²) is applied, as shown in Figure 3b, the time profile of the turn-off region is much broader than that of the pulse duration for the case of parallel fields because the response of the free electron is very sensitive to the external field and therefore the small field in the tail of the second pulse can be disturbed by the trajectory of the free electrons. The instantaneous response of the medium follows the intensity profile of the fundamental laser field which is similar to the variation of the HHG intensity for crossed polarizations as seen in Figure 3b. Figure 3b shows that the ionization and nonlinear refraction index would influence the phase mismatch on a short time scale. The variation of the dipole phase will play an important role in the phase mismatch associated with the second beam.

Figure 3: Variation of the intensity of harmonic H25 from argon gas versus delay between the two 800 nm laser pulses. The polarizations of the two beams are crossed and parallel. The intensity of the second beam is (a) 1×10¹³ W/cm2 and (b) 3×10¹³ W/cm².

Different responses can be observed depending on the molecule as shown in Figure 4. A fast and strong response is observed around zero delay time and a slow response can be seen for positive delay times which is different for N₂ (Figure 4a) and O₂ (Figure 4b) molecules. For a positive time delay the second pulse is used for non-adiabatic alignment of the molecules which leads to a change of the ionization rate and other nonlinear responses such as rotational or vibrational coherence. The variation of phase mismatch for positive time delay reflects the change in the ground state and can be used to study its dynamics.

Figure 4: Intensity of harmonic H27 from nitrogen gas (a) and intensity of harmonic H23 from oxygen gas (b) versus delay between the two 800 nm laser pulses. The polarizations of the two beams are crossed and parallel.

To increase the photon energy an increase of the laser intensity is required but then the ionization rate will be higher. The total phasemismatch is large and therefore the output harmonic field is very weak. In this case the off-axis field can be used to reduce the total phase mismatch and high harmonic orders can be obtained as shown in Figure 5 for harmonics from helium gas at 400 Torr.

Figure 5: High harmonic spectra from helium gas for different delay times between the two laser fields with same wavelength at 800 nm.

We note that the same effect is seen for HHG from argon gas but the generation of very high harmonic orders from helium will be more interesting. The harmonic spectrum is the variation with change of delay time between the two fields. The influence of the off-axis beam is strong for delay times of 0 fs and ± 30 fs when the intensity of the second laser field is high and a large variation of the dipole phase is expected. It has been shown [24] that without an off-axis beam in our configuration the shortest harmonic wavelength that can be obtained is~ 8.3 nm. Harmonics can be generated down to 7.3 nm and a second cut-off with low flux occurs down to ~ 5.5 nm.

Two laser fields with different wavelength: The Figure 6 shows the delay time dependence of the harmonic spectrum generated by a 1400 nm driving pulse. Two spectral areas are considered there by using of zirconium and alumina foil. When the delay time between the 800 and 1400 nm pulses is sufficiently long (-10 ps), the harmonic spectrum has a discrete structure, which is the same as that obtained from phase-matched generation without the 800 nm pulse. The polarizations of the two pulses are parallel. When the two pulses are overlapped (e.g. -15 fs and 5 fs) non-integer and even harmonic orders are clearly apparent. These intermediate harmonics are seen as two peaks between the harmonics of 1400 nm or four peaks between the harmonics of 800 nm. These are the result of frequency mixing, which induces a sub-cycle reshaping of the electric field. Their spacing is related to odd harmonics of the approximate minimum common multiple of the two wavelengths. The exact energy of the peak of these intermediate harmonics is observed to shift very slightly when the relative intensities are varied since these two sets of harmonics do not have the same periodicity. These photon energies, Eih, correspond exactly to a linear combination of the photon energies from both fields: Eih=nE1400+mE800 with (n+m) is being equal to an odd integer due to conservation of angular momentum. By careful variation of the 800 laser field an enhancement of the 1400 nm harmonic signal is observed. This enhancement is robust to changes of the relative delay up to several optical cycles. The yield enhancement is seen to be extremely sensitive to the relative and absolute values of the intensity of each field.

Figure 6: High harmonic spectra from argon gas for different delay times between the two laser fields. The laser pulses at 1400 nm and 800 nm are used for generation and control of the HHG process, respectively.

Non-instantaneous response to the second field

The variation of the HHG intensity from atomic gases as a result of the second beam is observed only around zero time delay where the second field interacts with the medium directly. The dephasing of the atomic gas is very fast and the atomic system is homogeneous when the second field is absent. The influence of the second beam on the HHG intensity of the molecular gases is very strong for positive time delays. The second pulse is used to non-adiabatically align the molecules and the rotational relaxation of the molecules is long. The lifetime of the in-homogeneous molecular ensemble is long and dependent on the molecular properties.

Figure 7 shows the dependence of the harmonic intensity of H27 for N₂ and H21 for O₂ on the time delay for long delay times between the two pulses. For a long positive time delay the intensity of all harmonics is modulated near T/4, T/2, 3T/4 and T, where T is the rotational period of the neutral N₂ (TN₂=8.4 ps [12]) and O₂ (TO₂=11.6 ps [12]) molecule for both parallel and crossed polarizations. The intensity modulations at T/4 and 3T/4 have opposite phase. A different phase is observed for N₂ and O₂ at T/4 and 3T/4.

Figure 7: Intensity of (a) harmonic H27 of aligned N₂ molecules and (b) H23 of aligned O₀ molecules versus delay between the two 800 nm beams. The inset shows the intensity of harmonic H27 from aligned N₂ molecules around T ͌ 8.4 ps versus delay between the two beams for different relative polarizations of the second beam (circles - parallel; triangles - crossed and squares - 54.70)

Without the aligning pulse (t<0), the molecular ensemble is isotropic. When interacting with the aligning pulse, each rotational |J> state within the rotational wave-packet accumulates phase with a different angular frequency. These rotational |J> states rapidly dephase with respect to each other and the initial net alignment quickly dissipates. Since the wave-packet evolves in a field-free environment, the |J> states eventually start to rephrase. When the accumulated phases of each |J> state are equal, the initial net alignment is reproduced in an event known as a wave-packet revival. The selection rule for Raman transitions is ΔJ=± 2. Therefore, at the time revivals T/4, T/2, 3T/4, T, the accumulated phases of states |J> and |J+2> differ by 2πp [19] and a significant net alignment and “anti-alignment” are observed.

A linearly polarized femtosecond laser pulse has a large spectral bandwidth that spans many rotational levels and thus can be used to create rotational wave packets and to induce non-adiabatic molecular alignment. When the femtosecond pulse is used to off-resonantly excite linear molecules such as N₂ and O₂, the pure rotational Raman refractive index Δn Raman (t) will contribute to the nonlinear refractive index Δn noninstant (λ,t) [25,26]. The non-instantaneous rotational Raman contribution depends on the transition probability between rotational levels which is different for different molecular configuration symmetry. For N₂ the transitions from even-J levels are two times more intense than those from odd-J levels and for O₂ only odd-J levels are populated.

The change of the nonlinear refractive index of N₂ and O₂ due to the Raman rotational motion Δn Raman (t) as a function of the delay time between the probe and pump beams can be simulated [26] and the results are shown in Figure 8. It is clear that both of the HHG signals are modulated at t=n*T/4. The simulation also shows that for two selected harmonics (H27 for N₂ and H21 for O₂) the modulation has the same phase at T/2 and T and opposite phase at T/4 and 3T/4. This agrees with the experimental observations. These results confirm that the phase-matching condition for the generation of harmonics in the observed spectral range varies following modulation of the Raman contribution to the total refractive index. For gases such as N₂ and O₂, since the rotational constant is equal to a few inverse centimeters, it can be understood that impulsive Raman excitation of rotational coherences can be induced with a single 100-fs pulse.

Figure 8: Simulations of the change of the nonlinear refractive index based on selection rules for rotational transitions in N2 and O2 molecules.

When the polarization of the second beam is rotated by 90o, the phase of the anisotropy of the molecular polarizability is inverted and therefore the modulation of the nonlinear refractive index is reversed. A modulation inversion of the harmonic intensity is observed when the polarizations are crossed as shown in the inset of Figure 7a (triangles) for H27 at time T. At the magic angle (θ ≈ 54.7o), only an isotropic response is measured. This leads to no change in the refractive index, i.e., there is no modulation of the harmonic intensity (squares).

We have demonstrated the importance of the atomic and molecular phase on the phase-matching of the HHG process. The phase mismatch can be altered by the use of a second delayed pulse which can enhance or destroy the HHG. The electron trajectories are strongly modified by two incommensurable laser fields which induce a sub-cycle reshaping of the electric field and frequency mixing can occur. Not only the dephasing due to intra- and intermolecular processes but also the electron configuration symmetry can be studied though the observed HHG radiation. This opens up a new technique for studying the coherence dynamics of atomic and molecular systems.