Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2015) Volume 4, Issue 3
We investigate whether previous evidence of the weakness of Tobin’s q ratio to explain variation in capital expenditure investment stems from ignoring R&D as an alternative investment. We develop and test modified q models that account for individual firms’ ex ante propensities to make these alternative types of investment. The structure of these models leads naturally to our use of propensity regression methodology in empirical tests. Using data on U.S. firms for 1974-2008, our approach yields strong and robust support for q theory. We also find evidence of the influence of financial constraints on investment.
<Keywords: Corporate investment, Tobin’s q, Capital expenditures, R&D, Propensity regression, Financial constraints
Corporate investment: accounting for alternative propensities
Tobin’s [1] neoclassical q theory posits that a firm has a marketbased incentive to invest; investment should increase with the ratio of the market value of the firm to the replacement cost of its existing capital. Yet researchers have struggled with the finding that Tobin’s q ratio has low power to explain variation in corporate investment, measured by capital expenditures. Previous studies have focused on two reasons for the weakness: (a) measurement error in q; and (b) financial constraints. We argue that this weakness may largely stem from ignoring R&D as an alternative investment.
Suppose q theory is true in the general sense that a firm’s incentive to invest increases with its relative market value. However, due to variations in industry and technology, individual firms vary in their propensities to make physical vs. intellectual property (IP) investment. Ideally, to test q theory each firm’s q ratio should be measured with separate respect to physical and IP capital, and separate regressions, of capital expenditures and R&D, should be estimated accordingly. However, this is not possible because the market values of a firm’s physical capital and intellectual property cannot be separately measured. So instead, researchers regress capital expenditures on q, measured as the ratio of the firm’s total market value to book capital. This regression will exhibit the classic errors-in-explanatory-variables problem because, while for some firms physical investment varies with q, for others IP investment varies with q. Thus, the coefficient of q will be biased toward zero, and the explanatory power of q will below.
Researchers have dealt indirectly with suspected measurement error in q by using consistent estimators for the coefficient of q. However, if the problem is largely due to ignoring cross-sectional variation in investment types, it may be possible to deal directly with the problem. For instance, if a researcher wishes to test q theory on physical investment, he or she could attempt to identify and include (exclude) firms that have a propensity to make capital expenditure (R&D) investment. Indeed, many extant empirical studies include only ‘manufacturing’ firms in their samples, defined as firms with SIC code values of 2000-3999. It may have been implicitly understood that ‘manufacturing’ firms would form an ideal sample in this regard. However, later we document that average R&D investment is substantial for ‘manufacturing’ firms, and is actually higher for ‘manufacturing’ firms than non-’manufacturing’ firms, raising the prospect that the specific measurement error problem we identify may largely explain the low power of q in capital expenditure regressions.
We deal with the problem formally by developing modified q models that allow for variation across firms in their propensities to make physical vs. IP investment. Our modified q models then lead naturally to the use of propensity regression methodology to test proposed determinants of investment, including and especially q. In a propensity regression of investment, variables proposed to explain variation in a given type of investment (i.e., state variables that determine the amount of investment) are weighted by a measure of each firm’s ex ante propensity to make that type of investment. Using data on U.S. firms for 1974-2008, our approach yields strong and robust empirical support for q theory. We also document evidence consistent with the influence of financial constraints on investment.
The paper proceeds as follows. Section 1 reviews the literature on measurement problems with q and develops modified q models of investment. Section 2 describes the data and discusses propensity regression methodology. Section 3 provides time series and crosssectional perspectives on the data. The main results are presented in Section 4. Section 5 presents results by industry. Section 6 summarizes.
Measurement error in q: Literature review and new modified q models of investment
We begin this section with a brief review of the q theory of investment and the literature on measurement problems associated with q. We then develop modified q models that account for individual firms’ propensities to make physical vs. IP investment. We conclude with an econometric analysis that describes how measurement error emerges from ignoring the problem of alternative types of investment.
q theory in brief: Key assumptions for the q theory of investment Tobin [1], Lucas and Prescott [2], Hayashi [3] are: (a) Capital markets are perfect (so financing and investment decisions are independent); (b) Fixed capital is homogeneous; and (c) Adjustment costs are convex in net investment. We denote the replacement cost of firm i’s physical capital at date t-1 as Ki,t-1, its time t physical investment as Ii,t, the economic depreciation rate of physical capital as δi, and the date t-1 ratio of the market value of physical capital to Ki,t-1 as qi,t-1. Then q theory states that firm i will invest until, at the margin, qi,t-1=1:
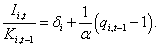 (1)
(1)
Hayashi [3] describes the conditions under which a firm’s average q ratio, denoted here as qi,t-1, is equal to its marginal value, qi,t-1. Virtually all empirical studies of the relationship between investment and Tobin’s q rely on Hayashi’s stipulation for the simple reason that average Q is empirically observable. We also utilize average Q in our modeling and empirics.
Measurement error in q: Literature review: In conventional regressions of capital expenditures, Q has performed poorly [4-7]. Some researchers attribute this poor performance to measurement error in Q which, as noted earlier, would have a deleterious effect on the explanatory power of Q. Moreover, the explanatory power of other variables in the regression, such as financial constraint variables (discussed later), would be enhanced if they inadvertently serve as instruments for Q [8].
Econometrically, two general remedies exist for the errors-inexplanatory- variables problem: (1) Improve the measurement of the explanatory variable; or (2) Use an econometric model that yields a consistent estimate of the coefficient of the mis-measured variable. Regarding remedy (1), researchers have devised and examined alternative proxies for Q [9-15]. Erickson and Whited [15] conclude that most proxies for Q are poor. However, Klock et al. [13] find that adding a measure of intangible (or intellectual) capital in the calculation of Q improves its performance. (Our measure of Q includes intellectual capital).
Studies applying remedy (2) include Abel and Blanchard [16], Blundell et al. [6], Cummins et al. [17], Gilchrist and Himmelberg [7], and Erickson and Whited [18]. These remedies have proved successful empirically in that the slope coefficient of Q in an investment regression is larger than is obtained using OLS regression [5,19]. However, these results cannot inform us about the specific source of the measurement error. Indeed, the evidence is consistent with our argument that measurement error in Q is an artifact of firms’ differential investment propensities. Next we develop alternative models that can help us assess the plausibility of this argument.
Modified q models of investment that account for alternative investment types
Empiricists have interpreted the ‘I’ and ‘K’ in the equation (1) as a firm’s capital expenditures and property, plant and equipment (PP and E), respectively [4,18,20-24]. However, these terms could instead refer to an alternative type of investment and its associated capital stock. This is an important issue because the U.S. economy has been evolving away from a ‘bricks and mortar’ economy dominated by physical investment toward a ‘knowledge’ economy with substantial IP investment in the form of R&D [25].
Here we construct modified q models of investment that allow for alternative types of investment. Though our approach can be applied to multiple types of investment, for simplicity we consider only capital expenditures and research and development (R&D) investment.1 In our setting each firm i at date t-1 is in a two-tiered state with respect to: (a) its ex ante propensities to make physical and IP investment; and (b) market conditions, measured by Q, that determine the amount of investment
Let 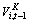 and
and 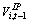 , denote the date t-1 market values of firm i’s physical capital and IP, respectively, Ki,t-1 and IPi,t-1 denote their respective replacement costs, and ,
, denote the date t-1 market values of firm i’s physical capital and IP, respectively, Ki,t-1 and IPi,t-1 denote their respective replacement costs, and ,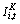 and ,
and , 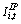 denote firm i’s time t physical and IP investment, respectively. Date t-1Q ratios associated with firm i’s physical and IP capital are given in equation (2) and (3), respectively,
denote firm i’s time t physical and IP investment, respectively. Date t-1Q ratios associated with firm i’s physical and IP capital are given in equation (2) and (3), respectively,
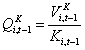 (2)
(2)
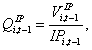 (3)
(3)
and, ignoring depreciation, q theory suggests the following separate investment-Q relationships:
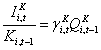 (4)
(4)
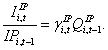 (5)
(5)
Unfortunately, as noted earlier we cannot observe the separate Q ratios for a firm’s physical and IP capital. We can only observe the firm’s overall Q ratio, denoted as qi,t-1, which we calculate as
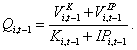 (6)
(6)
Defining p = IPi,t-1/ Ki,t-1, qi,t-1 can be re-expressed as
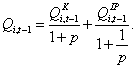 (7)
(7)
That is, qi,t-1 is a weighted average of the Q ratios of physical and IP capital.
We now consider the problem of modeling firm i’s physical investment given that: (a) the firm may also have a propensity to make IP investment; and (b) only the firm’s overall Q ratio, qi,t-1, is observable. Multiplying equation (4) through by Ki,t-1/( Ki,t-1+IPi,t-1) and then substituting an expression for , 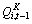 that can be obtained from equation (7) yields:
that can be obtained from equation (7) yields:
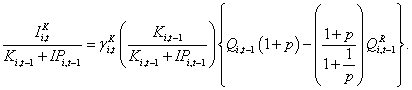 (8)
(8)
With additional manipulations (not shown for brevity), equation (8) can be re-expressed as
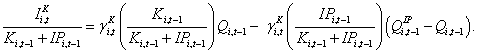 (9)
(9)
Equation (9) relates , 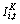 to qi,t-1, with the same coefficient, ,
to qi,t-1, with the same coefficient, , 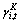 , as in equation (4). However, three additional features of this modified q model are important. First, ,
, as in equation (4). However, three additional features of this modified q model are important. First, , 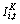 is scaled by firm i’s ‘total assets’ (i.e., Ki,t-1+IPi,t-1). Second, qi,t-1 is weighted by the fraction of firm i’s ‘total assets’ accounted for by physical capital. These features are intuitively appealing as they indicate that a firm’s capital expenditures depend not only on the Q ratio but also on the firm’s propensity to engage in capital expenditure investment.
is scaled by firm i’s ‘total assets’ (i.e., Ki,t-1+IPi,t-1). Second, qi,t-1 is weighted by the fraction of firm i’s ‘total assets’ accounted for by physical capital. These features are intuitively appealing as they indicate that a firm’s capital expenditures depend not only on the Q ratio but also on the firm’s propensity to engage in capital expenditure investment.
Third, the second term in equation (9) indicates that physical investment will be lower (higher) than as indicated by the first term to the extent that firm i has IP and 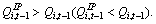 Unfortunately, in empirical tests of this model we cannot fully specify the second term in equation (90 because ,
Unfortunately, in empirical tests of this model we cannot fully specify the second term in equation (90 because ,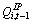 is unobservable. However, we can include a proxy for the second term, IPi,t-1/(Ki,t-1+IPi,t-1). This proxy should be correlated with the second term not only because the proxy is part of the second term, but also because the other part of the second term,
is unobservable. However, we can include a proxy for the second term, IPi,t-1/(Ki,t-1+IPi,t-1). This proxy should be correlated with the second term not only because the proxy is part of the second term, but also because the other part of the second term, 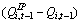 should be positively correlated with the proxy (i.e.,
should be positively correlated with the proxy (i.e., 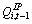 should be higher for firms with substantial IP).
should be higher for firms with substantial IP).
Next, we ask whether an alternative modified q model can be developed that relates a firm’s physical investment to its overall Q ratio but sans the weighting factor in equation (9). This question is important because all extant empirical studies relate a firm’s physical investment (i.e., capital expenditures) to its overall Q ratio without a weighting adjustment. The answer is yes. To do so, we initially re-express the second term in equation (9) as
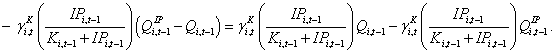 (10)
(10)
Next, multiplying equation (5) though by IPi,t-1/(Ki,t-1+IPi,t-1) yields
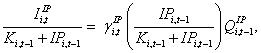 or
or 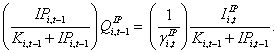
Substituting the RHS expression above into equation (10) yields the following alternative expression for the second term in equation (9):
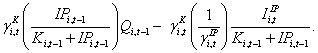
Finally, substituting this expression into equation (9) and noting that
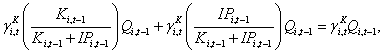
we obtain
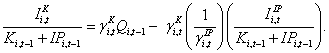 (11)
(11)
Equation (11) indicates that regressions of physical investment on the overall Q ratio will be downward biased to the extent that firms also, or alternatively, have a propensity to make IP investment, and this propensity is ignored. However, this bias may be at least partially corrected using the same proxy variable discussed in the context of the model in equation (9), IPi,t-1/(Ki,t-1+IPi,t-1).
Models analogous to equation (9) and equation (11) can be developed for IP investment. These models are given below as equation (12) and equation (13), respectively:
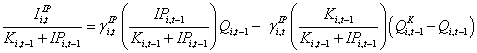 (12)
(12)
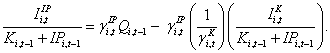 (13)
(13)
The analogous proxy for the second terms in equation’s (12) and (13) is Ki,t-1/(Ki,t-1+IPi,t-1).
Measurement error in q due to alternative investment types: econometric analysis
Next we analyze the problem of alternative investment types from an econometric viewpoint. Suppose a researcher intends to test q theory by regressing scaled physical investment on Q using OLS and a sample of firms of size N. Using notation from above, the regression equation is:
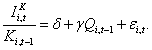 (14)
(14)
We assume that q theory is correct, but applies separately to physical and IP investment as discussed earlier. Thus, if all firms in the researcher’s sample are oriented to make only physical investment in response to Q, the OLS estimate of γ in equation (14) would be unbiased. However, suppose the sample actually consists of two subsamples of firms. The first (second) subsample, denoted as SK (SIP), consists of firms that are oriented to make only physical (IP) investment in response to Q, and is of size NK (NIP). The researcher ignores this fact, though, assuming instead that all firms in the full sample make only physical investment in response to Q. The OLS estimate of γ in equation (14) obtained using the full sample will be downward-biased relative to subsample SK and upward-biased relative to subsample SIP because the true value of γ is positive for the former and zero for the latter.
In the above scenario, the bias in γ can be seen in light of the classic errors in variables problem. The measurement error is associated with all firms in subsample SIP, for which actual values of Q should be replaced with zero (or, alternatively, these firms should be eliminated from the sample) because these firms do not make physical investment regardless of the value of Q. The critical question is: What is the extent of the bias in an OLS estimate of in equation (14), denoted as γOLS, if the researcher uses the full sample? To answer this question, let γK denote the true sensitivity of physical investment to Q for subsample SK, and Q’ denote ‘true’ values of Q, where Q’ is equal to Q for each firm in subsample SK and is equal to zero for each firm in subsample SIP. The equation for the classic errors in variables problem in the present context is then
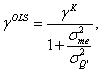 (15)
(15)
Where 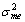 is the variance of the measurement error and
is the variance of the measurement error and 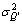 is the variance of Q’. Noting that the measurement error is equal to 0 (Q) for each firm in subsample SK (SIP), calculations (not shown) reveal that
is the variance of Q’. Noting that the measurement error is equal to 0 (Q) for each firm in subsample SK (SIP), calculations (not shown) reveal that
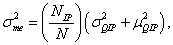 (16)
(16)
Where 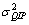 and μQIP are the variance and mean, respectively, of Q for subsample SIP. Additional calculations (not shown) reveal that
and μQIP are the variance and mean, respectively, of Q for subsample SIP. Additional calculations (not shown) reveal that
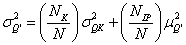 (17)
(17)
Where 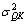 is the variance of Q (or equivalently, Q’) for firms in subsample SK evaluated against the mean value of Q’ for the full sample, Q’, and
is the variance of Q (or equivalently, Q’) for firms in subsample SK evaluated against the mean value of Q’ for the full sample, Q’, and 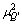 ' is the variance of Q’ for firms in subsample SIP (where Q’=0 for all firms in subsample SIP), also evaluated against γQ’.
' is the variance of Q’ for firms in subsample SIP (where Q’=0 for all firms in subsample SIP), also evaluated against γQ’.
Equation’s (15), (16), and (17) are consistent with intuition, suggesting that the bias in γOLS (i.e., γOLS-K) is an increasing function of (a) the relative number of IP-oriented firms in the full sample (i.e., NIP/N), as well as (b) both the variance and mean of Q for IP-oriented firms.2 However, the assumption that firms are completely bifurcated in terms of their investment orientation (i.e., physical vs. IP) is restrictive. This is why we use the propensity regression technique, discussed later, in our empirical analysis. The weighting scheme in propensity regression allows each firm to vary continuously in terms of their propensities for physical vs. IP investment. We will, however, use the econometric formulae developed here to generate rough preliminary estimates of bias.
Data
Our sample is drawn from the population of U.S. firms listed on NYSE, AMEX, and NASDAQ for the years 1974-2008. We exclude financial firms and utilities (SIC code values of 6000-6999 and 4900- 4949 resp.). We also exclude unseasoned firms by requiring that a firm has accounting and market data for fiscal years t-2 and t-1 as well as fiscal year t. To avoid the undue influence of very small firms, each year we exclude firms that are in the smallest 5% in terms of total assets or market equity value. The final sample includes 94,056 firm-year observations.
For each firm and year, we collect the following balance sheet and share-related variables from the Compustat fundamentals annual database for year-end t-1: total assets (TAt-1); net property, plant and equipment (PPENTt-1); total long-term debt (DLTTt-1); common equity book value (BEVt-1); price per share (PRCt-1); and common shares outstanding (CSHOt-1). Market equity value, MEVt- 1, is calculated as MEVt-1= PRCt-1*CSHOt-1, We also collect the following flow variables for fiscal years indicated by subscripts: operating activity net cash flow (OANCFt); total dividends paid (DIVt,); capital expenditures (CAPXt); R&D expenditures (R&Dt, R&Dt-1, …, R&Dt-5); net debt financing (NETDTt, the difference of debt issuances and retirements); and net equity financing (NETEQt, the difference of stock issuances and repurchases). We measure internal net cash flow as NCFt=OANCFt- DIVt+R&Dt. This calculation reflects: (a) our treatment of dividends as a de facto firm commitment to shareholders; and (b) the adding-back of R&D so that it has status as a decision variable rather than a fait accompli.
We also need to estimate a firm’s R&D capital (because R&D is expensed rather than capitalized). Following Chan, Lakonishok, and Sougiannis, we estimate R&D capital using a 20% straight-line depreciation rate on R&D spending for the five years ending at yearend t-1, denoting this estimate as R&DCAPt-1. We then calculate an augmented measure of a firm’s year-end t-1 total assets: TA’t-1=TAt- 1+R&DCAPt-1, and scale all variables by TA’t-1. This includes Tobin’s Q, calculated as Qt-1=(TA’t-1-BEVt-1+MEVt-1)/TA’t-1, and leverage, calculated as LEVt-1=DLTTt/TA’t-1. All scaled variables are winsorized at the 1% and 99% levels.
We also need each firm’s SIC code value for various industry analyses. SIC code values are available in Compustat only after 1987, so we use SIC code values from CRSP, and use Compustat SIC code values only if the CRSP value is missing. For industry analysis in Section 7, we use the five industry categories defined on Ken French’s website: Hightech; Healthcare; Consumer; Manufacturing and Energy; and Other.
Finally, in some analyses we segregate firms by a size and age combination. A firm is designated as small/young if (a) MEVt-1 is below the median MEVt-1 of all firms in its industry and (b) the firm has been publicly traded for six or fewer years as of year-end t-1. All other firms are designated as large/mature.
Methodology
The form of our main modified q models (equation’s (9) and (12)) leads naturally to our use of propensity regression methodology. As applied in the present context, in a propensity regression variables hypothesized to effect of the amount of a given type of investment (e.g., Qt-1 and NCFt/TA’t-1) are weighted by the firm’s ex ante propensity to make that type of investment. We assess the efficacy of propensity regression by comparing results to those of (un-weighted) OLS/GLM regression alternatives.
Some background on propensity regression is in order. Rubin [26] and Rosenbaum and Rubin [27,28] develop a propensity score matching (PSM) technique to deal with the ‘missing data’ problem in nonrandomized (as opposed to experimental) settings. In such a setting it is difficult to attribute differences in responses, Y, to treatment X if an unobserved intervening variable Z covaries with both X and Y. To alleviate this problem, the researcher tests the effect of X on Y using pairs of observations that are matched in terms of ‘scores’ based on proxies for Z.
PSM has been used in many disciplines, including economics and finance. In economics, Dehejia and Wahba [29], Heckman, Ichimura, and Todd [30] and Lechner [31,32] all use PSM in the context of job training analysis. In finance, Li and Zhao [33] use PSM to investigate the abnormal performance of firms following seasoned equity offerings, Hellman, Lindsey, and Puri use PSM to investigate the relationship between a bank’s venture capital investments and its subsequent lending, Lin and Su use PSM to investigate the relationship between diversification and firm value, Ivanov and Xie [34] use PSM to determine when venture capitalists add value to startups, Xuan [35] uses PSM in the context of internal capital allocation decisions in multidivisional firms, and Demiroglu, James, and Kizilaslan [36] use PSM in their study of bank lending standards and lines of credit.
Recently, the PSM concept has been extended to regression analysis [37-40]. Freedman and Berk [41] explain propensity regression as a two-step process:
Step 1: A model (typically logit or probit) is used to estimate the probability of selection into the treatment and control group.
Step 2: Estimated probabilities from the first step are used to construct weights. The weights are then used to fit the causal model…” (p. 11). Our propensity regression design follows Freedman and Berk’s two-step process, with the proviso that our main modified q models already indicate the appropriate propensity weight for each type of investment: PPENTt-1/TA’t-1 for capital expenditures and R&DCAPt-1/ TA’t-1 for R&D.
Time series perspectives
Figure 1 shows annual averages of PPENTt-1/TA’t-1, R&DCAPt-1/ TA’t-1, CAPXt/TA’t-1, R&Dt/TA’t-1, and Qt-1 for 1974-2008. Average values of PPENTt-1/TA’t-1 and CAPXt/TA’t-1 generally fall over the years, while average values of R&DCAPt-1/TA’t-1, R&Dt/TA’t-1, and Qt-1 generally rise. Thus, U.S. firms collectively were undergoing a gradual, though profound, transformation in asset composition and investment over the years, away from (toward) physical (IP) capital intensity. In addition, the results in Figure 1 warn of the potential hazard of focusing only on capital expenditure investment, especially if analysis is conducted using more recent data. Indeed, on average R&Dt/TA’t-1 nearly reaches parity with CAPXt/TA’t-1 by 2002.
In recognition of this transformation, in subsequent analyses we often divide the sample into two subperiods that we call the ‘Old Economy,’ 1974-87, and the ‘New Economy,’ 1988-2008. The dividing year for the split is admittedly somewhat arbitrary because the trends in Figure 1 are fairly gradual. We start the New Economy in 1988 for three reasons. First, average R&Dt/TA’t-1 was less than one-third of average CAPXt/TA’t-1 until 1988. Second, many of the corporate governance reforms discussed earlier occurred in the 1980s or later, so the split should be useful in tests of the effects of corporate governance reform on prevalence of empire builders and their effect on ICF sensitivity in capital expenditure regressions. Third, while NASDAQ was established in 1971, initial public offerings (IPOs) of small-firm stocks did not accelerate until the 1980s, after federal legislation was passed that fostered the development of the venture capital industry [42]. Thus, the split should also be useful in tests of the equity-market development hypothesis.
Cross-sectional perspectives
Next, we calculate average values of CAPXt/TA’t-1, R&Dt/TA’t-1, PPENTt-1/TA’t-1, R&DCAPt-1/TA’t-1, and Qt-1 for various sorts of the data. The results are displayed in Table 1. Results for the full sample are shown in Panel A, while Panels B and C show results for ‘manufacturing’ firms (as defined in prior literature) and non-’manufacturing’ firms (all other firms), respectively. We segregate ‘manufacturing’ firms because many previous empirical studies of corporate investment exclusively use samples of ‘manufacturing’ firms, and focus only on capital expenditure investment.3 Each panel shows results for (a) all firm-years; (b) Old vs. New Economies; and (c) ranges of PPENTt-1/ TA’t-1. (Results of sorting by ranges of R&DCAPt-1/TA’t-1, not shown, mirror those of sort (c)).
| Economy | Ranges of x=(PPENTt-1/TA't-1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variable: | All Years | Old | New | Diff. | x<0.10 | 0.10≤x | 0.20≤x | 0.30≤x | x≥0.40 | Diff. |
| (New-Old) | <0.20 | <0.30 | <0.40 | (High-Low) | ||||||
| Panel A: All firms | ||||||||||
| CAPXt/TA't-1 | 0.072 | 0.087 | 0.066 | -0.021 *** | 0.027 | 0.047 | 0.064 | 0.082 | 0.131 | 0.104 *** |
| R&Dt/TA't-1 | 0.029 | 0.017 | 0.035 | 0.018 *** | 0.065 | 0.038 | 0.025 | 0.016 | 0.004 | -0.061 *** |
| PPENTt-1/TA't-1 | 0.292 | 0.338 | 0.271 | -0.067 *** | 0.054 | 0.15 | 0.248 | 0.346 | 0.601 | 0.547 *** |
| R&DCAPt-1/TA't-1 | 0.07 | 0.037 | 0.085 | 0.048 *** | 0.159 | 0.088 | 0.057 | 0.038 | 0.01 | -0.149 *** |
| Qt-1 | 1.65 | 1.266 | 1.827 | 0.561 *** | 2.056 | 1.697 | 1.56 | 1.467 | 1.448 | -0.607 *** |
| N | 94,056 | 29,720 | 64,336 | 19,390 | 20,004 | 17,619 | 12,511 | 24,532 | ||
| N as % | 100.00% | 31.60% | 68.40% | 20.60% | 21.30% | 18.70% | 13.30% | 26.10% | ||
| Panel B: 'Manufacturing' firms | ||||||||||
| CAPXt/TA't-1 | 0.059 | 0.074 | 0.051 | -0.022 *** | 0.027 | 0.045 | 0.06 | 0.076 | 0.099 | 0.072 *** |
| R&Dt/TA't-1 | 0.039 | 0.023 | 0.048 | 0.025 *** | 0.085 | 0.046 | 0.03 | 0.021 | 0.01 | -0.075 *** |
| PPENTt-1/TA't-1 | 0.252 | 0.297 | 0.228 | -0.070 *** | 0.056 | 0.151 | 0.248 | 0.346 | 0.53 | 0.475 *** |
| R&DCAPt-1/TA't-1 | 0.093 | 0.051 | 0.116 | 0.065 *** | 0.208 | 0.106 | 0.07 | 0.05 | 0.023 | -0.185 *** |
| Qt-1 | 1.614 | 1.231 | 1.826 | 0.596 *** | 2.127 | 1.661 | 1.505 | 1.407 | 1.338 | -0.789 *** |
| N | 53,259 | 18,974 | 34,285 | 9,781 | 13,253 | 12,625 | 8,504 | 9,096 | ||
| N as % | 100.00% | 35.60% | 64.40% | 18.40% | 24.90% | 23.70% | 16.00% | 17.10% | ||
| Panel C: Non-'manufacturing' firms | ||||||||||
| CAPXt/TA't-1 | 0.09 | 0.111 | 0.082 | -0.028 *** | 0.026 | 0.053 | 0.074 | 0.095 | 0.149 | 0.123 *** |
| R&Dt/TA't-1 | 0.017 | 0.006 | 0.021 | 0.015 *** | 0.045 | 0.023 | 0.011 | 0.005 | 0.001 | -0.044 *** |
| PPENTt-1/TA't-1 | 0.344 | 0.409 | 0.321 | -0.089 *** | 0.051 | 0.148 | 0.248 | 0.348 | 0.643 | 0.591 *** |
| R&DCAPt-1/TA't-1 | 0.039 | 0.012 | 0.049 | 0.037 *** | 0.109 | 0.051 | 0.025 | 0.013 | 0.003 | -0.107 *** |
| Qt-1 | 1.696 | 1.328 | 1.828 | 0.500 *** | 1.983 | 1.766 | 1.7 | 1.594 | 1.513 | -0.469 *** |
| N | 40,797 | 10,746 | 30,051 | 9,609 | 6,751 | 4,994 | 4,007 | 15,436 | ||
| N as % | 100.00% | 26.30% | 73.70% | 23.60% | 16.50% | 12.20% | 9.80% | 37.80% | ||
Notes: Shown are average values of investment measures and related variables, calculated for the full sample of U.S. firm-years and for sorts by Economy (Old (1974- 87) vs. New (1988-2008)) or indicated ranges of physical capital intensity (PPENTt-1/TA't-1). Panel A shows results for all firms, while Panels B and C show results for 'manufacturing' and non-'manufacturing' firms, respectively, where 'manufacturing' firms are defined as those with SIC code values of 2000-3999. Significance indicators for differences: *** (1%); ** (5%); *(10%).
Table 1: Average Values of Investment, Capital, and Q by Economy, 'Industry' and Physical Capital Intensity.
Panel A shows that average values of CAPXt/TA’t-1 and PPENTt-1/ TA’t-1 (R&Dt/TA’t-1, R&DCAPt-1/TA’t-1, and Qt-1) are substantially and reliably lower (higher) in the New Economy than the Old, consistent with trends shown in Figure 1. More importantly, average values of CAPXt/TA’t-1 (R&Dt/TA’t-1 and R&DCAPt-1/TA’t-1) increase (decrease) monotonically, sharply, and reliably with PPENTt-1/TA’t-1, indicating that PPENTt-1/TA’t-1 (R&DCAPt-1/TA’t-1) is a strong measure of individual firms’ propensities to make capital expenditure (R&D) investment.
The results for CAPXt/TA’t-1 (though not for R&Dt/TA’t-1) across ranges of PPENTt-1/TA’t-1 are potentially problematic for q theory because average CAPXt/TA’t-1 increases, while average Qt-1 decreases, monotonically with PPENTt-1/TA’t-1. However, these results can be reconciled as follows. Suppose we have data in which individual firms vary in their propensities to make capital expenditure vs. R&D investment, and the cross-sectional covariance of these propensities is negative, though for each firm investment tends to increase with Q. If we then sort the data into classes by ranges of a propensity measure associated with one investment type, the sort will produce opposing trends in average values of capital expenditures vs. R&D investment. However, whether Q tends to increase or decrease across the classes depends on which investment type is generally associated with higher Q values (i.e., with greater investment opportunities). For our data, that investment type apparently is R&D, which in turn explains the time trends in Figure 1 away from capital expenditures and toward R&D.
Finally, we briefly discuss the results in Panels B and C for ‘manufacturing’ and non-’manufacturing’ firms. All inferences drawn from our analysis of results in Panel A also apply to the results in Panels B and C, attesting to their robustness. However, the results in Panels B and C differ in one important respect: For all years combined as well as for the Old and New Economies, average values of CAPXt/TA’t-1 and PPENTt-1/TA’t-1 (R&Dt/TA’t-1 and R&DCAPt-1/TA’t-1) are substantially lower (higher) for ‘manufacturing’ firms than for non-’manufacturing’ firms. These results are surprising given the large number of studies that have used ‘manufacturing’ firms in studies of capital expenditure investment. Apparently, subsequent studies simply followed Fazarri et al. [4] lead in choosing ‘manufacturing’ firms, perhaps assuming that ‘manufacturing’ firms, as defined, represent the ideal class of firms for studying capital expenditure investment. If so, they did so despite Poterba’s [43] caveat in his comments on Fazarri et al. [4] analysis: “It is even more difficult to generalize to nonmanufacturing firms, which held over 70 percent of corporate plant and equipment at the end of 1986. In any event, the relatively high average IP intensity of ‘manufacturing’ firms suggest that, if our hypothesis about the confounding effects of alternative investment types is correct, using these firms would be especially problematic, rather than ideal.
Preliminary estimates of bias
For our final preliminary analysis, we use sample statistics to generate implied estimates of the bias in the OLS estimate of the coefficient of Qt-1 in regressions of capital expenditures (CAPXt/ TA’t-1). Specifically, we estimate the bias factor, BF, which forms the denominator in equation (15); i.e. 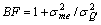 , where
, where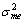 and
and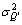 are defined in equation’s (16) and (17). Following this framework, we divide the observations in our full sample (N=94,056) into subsamples SK and SIP according to whether the year t-1 value of R&D expenditures is zero or positive, respectively, resulting in subsamples of sizes NK=48,690 and NIP=45,366. Values of the other relevant statistics are:
are defined in equation’s (16) and (17). Following this framework, we divide the observations in our full sample (N=94,056) into subsamples SK and SIP according to whether the year t-1 value of R&D expenditures is zero or positive, respectively, resulting in subsamples of sizes NK=48,690 and NIP=45,366. Values of the other relevant statistics are: 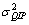 = 1.454; μQIP = 1.813; 2
= 1.454; μQIP = 1.813; 2 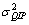 = 0.863; and μQ’ = 0.776.
= 0.863; and μQ’ = 0.776.
As shown in Table 2 Panel A, the resulting estimate of BF is 4.102. The inverse of this estimate, also shown, is 0.244. Referring to equation (15), the latter estimate suggests that for our full sample an OLS estimate of the sensitivity of capital expenditure investment to Q, γOLS, will be only about one-quarter of the ‘true’ sensitivity for firms oriented toward capital expenditure investment (i.e., subsample SK). This result is important as it suggests that results of a basic test of q theory for capital expenditure investment would be severely biased due to the presence of firms that are oriented instead toward R&D investment.
| Panel A. Estimate of implied measurement error bias factor (BF) from Eq. (15) | |||
|---|---|---|---|
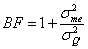 |
|||
| Estimate of BF: | 4.102 | ||
| 1/( Estimate of BF): | 0.244 | ||
| Panel B. Estimates of measurement error bias via OLS regression (Dep. Var. = CAPXt /TA' t-1 ) | |||
| Intercept | Qt-1 | Q't-1 | Adj. R2 |
| 0.061 | 0.007 | 0.009 | |
| 128.16 | 29 | ||
| 0.057 | 0.02 | 0.062 | |
| 177.73 | 78.71 | ||
| Estimate of 1/BF: | 0.351 | ||
Notes: Results are for U.S. firms, 1974-2008.
Table 2: Estimates of Bias in the Coefficient of Q in Capital Expenditure Regressions.
For comparative purposes, we also take a second approach to bias estimation that is more direct. We regress year t capital expenditures on values of either Qt-1 or Q’t-1, where Q’t-1 is as defined in section 1.4; i.e., Q’t-1 is equal to Qt-1 (0) for firms in subsample SK (SIP). These regressions are estimated by applying OLS to the full sample. The results are displayed in Table 2 Panel B.
Using Qt-1 as the regressor, the slope coefficient is 0.007 (t-value=29.00) and the adjusted R2 is 0.009. Thus, the coefficient of Qt-1 is reliably positive as expected; however, we obtain the familiar result that Q has very little power to explain variation in capital expenditure investment. The results of using Q’t-1, however, are markedly stronger. For this regression both the slope coefficient and the adjusted R2 are substantially higher, 0.020 (t-value=78.71) and 0.062, respectively. Moreover, our estimate of the inverse of the bias factor, 1/BF, which here is calculated as the ratio of the slope coefficients in the first and second regressions, is 0.351, which is very similar to the indirect estimate shown in Panel A (0.244). Thus, though both approaches used here to estimate investment-propensity induced measurement-error bias are crude, the results strongly suggest that ignoring investment propensities will induce substantial bias in investment-Q regressions.
This section provides results investment regressions with alternative specifications. In all regressions the weight applied to regressors is denoted as pwt-1. In propensity regressions of capital expenditures (R&D), pwt-1=PPENTt-1/TA’t-1 (pwt-1=R&DCAPt-1/TA’t-1), while in all un-weighted regressions pwt-1=1.0.
Preliminary investment regressions
We initially test alternative q models, including the basic q model and the modified models developed in Section 2. Tests of the basic q model simply involve OLS regression of a focal investment measure on Qt-1. The modified q models given in equation’s (11) and (13) are also tested via OLS, and simply involve adding the opposing investment measure to the basic q model. Finally, we use propensity regressions to test our main modified q models, given in equation’s (9) and (12). The results are shown in Table 3 Panels A and B for capital expenditures and R&D, respectively. In each panel, we initially use full-sample data, then subsamples for the Old vs. New Economy and for large/mature vs. small/young firms.
| Sample | N | pwt -1 | Intercept | pwt -1*Qt -1 | CAPXt/TA't-1 | Adj. R2 |
|---|---|---|---|---|---|---|
| Panel A: Dep. var.=CAPXt /TA' t-1 | ||||||
| All Firm/Years | 94,056 | 1 | 0.061 *** | 0.007 *** | 0.009 | |
| 1 | 0.062 *** | 0.012 *** | -0.331 *** | 0.049 | ||
| PPENTt-1/TA't-1 | 0.030 *** | 0.097 *** | 0.272 | |||
| PPENTt-1/TA't-1 | 0.033 *** | 0.095 *** | -0.089 *** | 0.276 | ||
| Old Economy | 29,720 | 1 | 0.059 *** | 0.022 *** | 0.041 | |
| 1 | 0.059 *** | 0.026 *** | -0.279 *** | 0.051 | ||
| PPENTt-1/TA't-1 | 0.040 *** | 0.112 *** | 0.241 | |||
| PPENTt-1/TA't-1 | 0.040 *** | 0.112 *** | -0.009 | 0.241 | ||
| New Economy | 64,336 | 1 | 0.052 *** | 0.007 *** | 0.012 | |
| 1 | 0.055 *** | 0.012 *** | -0.312 *** | 0.06 | ||
| PPENTt-1/TA't-1 | 0.023 *** | 0.094 *** | 0.305 | |||
| PPENTt-1/TA't-1 | 0.026 *** | 0.092 *** | -0.065 *** | 0.307 | ||
| Large/Mature Firms | 78,108 | 1 | 0.061 *** | 0.007 *** | 0.009 | |
| 1 | 0.062 *** | 0.012 *** | -0.334 *** | 0.047 | ||
| PPENTt-1/TA't-1 | 0.029 *** | 0.097 *** | 0.283 | |||
| PPENTt-1/TA't-1 | 0.032 *** | 0.095 *** | -0.085 *** | 0.286 | ||
| Small/Young Firms | 15,948 | 1 | 0.061 *** | 0.007 *** | 0.008 | |
| 1 | 0.065 *** | 0.012 *** | -0.331 *** | 0.057 | ||
| PPENTt-1/TA't-1 | 0.032 *** | 0.098 *** | 0.237 | |||
| PPENTt-1/TA't-1 | 0.038 *** | 0.094 *** | -0.115 *** | 0.243 | ||
| Panel B: Dep. var.=R&Dt /TA't-1 | ||||||
| All Firm/Years | 94,056 | 1 | 0.004 *** | 0.016 *** | 0.107 | |
| 1 | 0.011 *** | 0.016 *** | -0.123 *** | 0.143 | ||
| R&Dt-1/TA't-1 | 0.012 *** | 0.119 *** | 0.609 | |||
| R&Dt-1/TA't-1 | 0.014 *** | 0.118 *** | -0.031 *** | 0.611 | ||
| Old Economy | 29,720 | 1 | 0.002 *** | 0.012 *** | 0.086 | |
| 1 | 0.004 *** | 0.013 *** | -0.038 *** | 0.095 | ||
| R&Dt-1/TA't-1 | 0.008 *** | 0.156 *** | 0.57 | |||
| R&Dt-1/TA't-1 | 0.009 *** | 0.156 *** | -0.005 *** | 0.57 | ||
| New Economy | 64,336 | 1 | 0.008 *** | 0.015 *** | 0.091 | |
| 1 | 0.016 *** | 0.016 *** | -0.156 *** | 0.135 | ||
| R&Dt-1/TA't-1 | 0.013 *** | 0.116 *** | 0.607 | |||
| R&Dt-1/TA't-1 | 0.016 *** | 0.115 *** | -0.043 *** | 0.61 | ||
| Large/Mature Firms | 78,108 | 1 | 0.002 *** | 0.015 *** | 0.114 | |
| 1 | 0.009 *** | 0.016 *** | -0.115 *** | 0.148 | ||
| R&Dt-1/TA't-1 | 0.011 *** | 0.116 *** | 0.615 | |||
| R&Dt-1/TA't-1 | 0.014 *** | 0.116 *** | -0.029 *** | 0.617 | ||
| Small/Young Firms | 15,948 | 1 | 0.012 *** | 0.016 *** | 0.085 | |
| 1 | 0.022 *** | 0.018 *** | -0.151 *** | 0.131 | ||
| R&Dt-1/TA't-1 | 0.015 *** | 0.127 *** | 0.587 | |||
| R&Dt-1/TA't-1 | 0.018 *** | 0.125 *** | -0.039 *** | 0.59 | ||
Notes: Results of OLS and propensity regressions of capital expenditures (Panel A) and R&D (Panel B). Propensity weight is pwt-1, and OLS regression is indicated by pwt-1=1.0. Results are alternately for all firm/years, Old Economy vs. New Economy years (1974-87 vs. 1988-2008), and large/mature vs. small/young firms. Significance indicators: *** (1%); **(5%); *(10%).
Table 3: Preliminary OLS and Propensity Regressions of Capital Expenditure and R&D Investment
The first row of Panel A shows results for the basic q model on capital expenditures using full-sample data. The coefficient of Qt-1 is positive and highly significant; however, we obtain the familiar paltry explanatory power, as the adjusted R2 is only 0.009. The second row shows results for the modified q model of equation (11). The coefficient of the opposing investment measure, R&Dt/TA’t-1, is negative, as expected, and highly significant. In addition: (a) The coefficient of Qt-1 increases markedly to 0.012 from 0.007 in the basic q model regression; and (b) The adjusted R2 increases markedly to 0.049 from 0.009. These results provide another indication of the importance of accounting for alternative investment types in testing q theory.
The third row shows results of a propensity regression of CAPXt/ TA’t-1 on Qt-1. The coefficient of pwt- 1*Qt-1 is positive and highly significant, though the value of the coefficient, 0.097, is not directly comparable to the values of the coefficient of Qt-1 in the previous OLS regressions due to propensity weighting. Moreover, the adjusted R2 of this regression, 0.272, is far higher than the adjusted R2s in the previous two regressions. As such, the results strongly support both our modified model and propensity regression methodology.
To form the fourth regression we add the (un-weighted) opposing investment measure, R&Dt/TA’t-1, as a proxy for the second term in equation (9). The coefficient of R&Dt/TA’t-1 is reliably negative. However, the coefficient is relatively small, -0.089, and the addition of this variable adds little to the adjusted R2; 0.276 vs. 0.272 in the previous propensity regression. Thus, propensity modeling and methodology essentially obviates the need for the opposing-investment variable, as expected.
The results of using subsample data for the Old vs. New Economies and large/mature vs. small/young firms, shown in the remainder of Panel A, are very similar to those for the full sample. Thus, we simply note that the subsample results attest to the robustness of our modeling and methodology.
The results in Panel B, for R&D investment, are qualitatively similar to those in Panel A. For the full sample, the first regression, testing the basic q model, yields a reliably positive coefficient of Qt-1. The adjusted R2, 0.106, is low relative to later regressions, but is high relative to the corresponding regression in Panel A. In the second regression, the coefficient of the added opposing investment measure, CAPXt/TA’t-1, is negative, as expected, and highly significant, and the addition of this variable boosts the adjusted R2 to 0.142. In the third regression, the coefficient of pwt*Qt-1 is reliably positive, and the adjusted R2, 0.609, is very large. These results indicate that after adjusting for propensity, R&D investment is highly sensitive to Q. When we add the opposing (un-weighted) investment measure CAPXt/TA’t-1 to form the fourth regression, its coefficient is relatively small and the adjusted R2 increases only slightly (to 0.611), indicating again that propensity modeling and methodology adequately accounts for alternative investment types.
Finally, the results of using subsamples for the Old vs. New Economies and large/mature vs. small/young firms, shown in the remainder of Panel B, are very similar to those for the full sample, so we only note that the results attest to robustness.
Adding a financial constraint variable and fixed effects
Next, we add the internal net cash flow variable NCFt/TA’t-1, as well as fixed year and firm effects, as explanatory variables in both conventional and propensity regressions. Regarding internal net cash flow, many previous studies include a measure of internal net cash flow to gauge the effects of financial constraints on external financing of investment, though the justification for doing so has been hotly debated.4 Fixed effects are also commonly added to account for unobserved factors [4,21,23-25,44]. While we accept this justification, we suspect that the explanatory power of fixed effects is due, at least in part, to individual firms’ differential investment propensities. For instance, in conventional regressions of either capital expenditures or R&D, fixed year effects would tend to capture the general trends in these variables over time as shown in Figure 1. However, propensity weighting would also tend to capture these trends, as the parallel trends in PPENTt-1/TA’t-1 and R&DCAPt-1/TA’t-1 indicate. Regarding fixed firm effects, evidence in Tables 1 and 3 suggest that our propensity proxies PPENTt-1/TA’t-1 and R&DCAPt-1/TA’t-1 explain substantial portions of cross-sectional variation in investment of each type.
For this analysis we use full-sample data, and to accommodate fixed effects we use the GLM. Results are shown in Table 4 Panels A and B for capital expenditures and R&D, respectively. The first five regressions in Panel A are conventional OLS/GLM regressions, denoted by pwt- 1=1.0. In the first regression Qt-1 is the sole regressor. The results are therefore identical to those in the first row of Table 3 Panel A. The second regression is formed by adding NCFt/TA’t-1 as a regressor. The coefficient of NCFt/TA’t-1 is reliably positive, and the adjusted R2 increases substantially to 0.078. Fixed year effects are added to form the third regression. Their addition increases both the coefficient of Qt-1 (to 0.008 from 0.005) and the adjusted R2 (to 0.110 from 0.078), while the coefficient of NCFt/TA’t-1 falls slightly (to 0.178 from 0.187).
| Fixed effects: | pwt-1* | OLS adj. R2 or GLM R2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| pwt-1 | Year? | Firm? | Intercept | Qt-1 | NCFt/TA't-1 | ||||
| PanelA: Dep.var.=CAPXt/TA't-1 | |||||||||
| 1.0 | No | No | 0.061*** | 0.007*** | 0.009 | ||||
| 1.0 | No | No | 0.047*** | 0.005*** | 0.187*** | 0.078 | |||
| 1.0 | Yes | No | 0.008*** | 0.178*** | 0.110 | ||||
| 1.0 | No | Yes | 0.014*** | 0.132*** | 0.571 | ||||
| 1.0 | Yes | Yes | 0.015*** | 0.115*** | 0.594 | ||||
| PPENTt-1/TA't-1 | No | No | 0.030*** | 0.097*** | 0.272 | ||||
| PPENTt-1/TA't-1 | No | No | 0.024*** | 0.061*** | 0.693*** | 0.389 | |||
| PPENTt-1/TA't-1 | Yes | No | 0.063*** | 0.661*** | 0.407 | ||||
| PPENTt-1/TA't-1 | No | Yes | 0.048*** | 0.500*** | 0.595 | ||||
| PPENTt-1/TA't-1 | Yes | Yes | 0.047*** | 0.448*** | 0.613 | ||||
| Panel B: Dep.var.=R&Dt/TA't-1 | |||||||||
| 1.0 | No | No | 0.004*** | 0.016*** | 0.107 | ||||
| 1.0 | No | No | 0.000 | 0.015*** | 0.051*** | 0.119 | |||
| 1.0 | Yes | No | 0.013*** | 0.057*** | 0.132 | ||||
| 1.0 | No | Yes | 0.004*** | 0.048*** | 0.853 | ||||
| 1.0 | Yes | Yes | 0.002*** | 0.053*** | 0.861 | ||||
| R&DCAPt-1/TA't-1 | No | No | 0.012*** | 0.119*** | 0.609 | ||||
| R&DCAPt-1/TA't-1 | No | No | 0.009*** | 0.106*** | 0.643*** | 0.684 | |||
| R&DCAPt-1/TA't-1 | Yes | No | 0.106*** | 0.640*** | 0.685 | ||||
| R&DCAPt-1/TA't-1 | No | Yes | 0.037*** | 0.408*** | 0.874 | ||||
| R&DCAPt-1/TA't-1 | Yes | Yes | 0.037*** | 0.403*** | 0.875 | ||||
Notes: Results of OLS/GLM and propensity regressions of capital expenditures (Panel A) and R&D (Panel B) on Tobin’s Q (Qt-1) and operating net cash flow (NCFt/TA't-1). Propensity weight is pwt-1, and OLS/GLM regression is indicated by pwt-1=1.0. The inclusion of fixed year and/or firm effects is indicated. Results are for all firm/years (1974- 2008; N=94,056). Significance indicators: *** (1%); ** (5%); * (10%).
Table 4: OLS/GLM and Propensity Regressions of Capital Expenditures and R&D Investment.
The fourth regression includes fixed firm effects, but not fixed year effects. Their addition has dramatic effects relative to the second regression, as: (a) The coefficient of Qt-1 increases to 0.014 from 0.005; (b) The coefficient of NCFt/TA’t-1 decreases to 0.132 from 0.187; and (c) The GLM R2 is 0.571, vs. an adjusted R2 of 0.078 in the second regression. The fifth regression includes both fixed year and fixed firm effects. Relative to the second regression, their combined addition dramatically increases (decreases) the coefficient of Qt-1 (NCFt/TA’t-1), and the GLM R2 is very high at 0.571. These results represent new evidence on the power of fixed effects to explain variation in capital expenditures in conventional regressions because previous studies (noted above) do not report separate regression results with and without fixed effects. Moreover, the results do not bode well for q theory because fixed effects account for most of the explained variation in investment.
The last five of regressions in Panel A are propensity regressions, denoted by pwt-1=PPENTt-1/TA’t-1. In the sixth regression pwt-1*Qt-1 is the sole regressor. As in the third row of Table 3 Panel A, we find a substantial adjusted R2 of 0.272. The seventh regression is formed by adding pwt- 1*NCFt/TA’t-1 as a regressor. The coefficient of pwt-1*NCFt/TA’t-1 is reliably positive and the adjusted R2 increases substantially to 0.389 from 0.272 in the first regression. When fixed year effects are added to form the eighth regression, the GLM R2 is only slightly higher than the adjusted R2 of the previous regression, 0.407 vs. 0.389. When fixed firm effects are added instead, the GLM R2 increases much more substantially, to 0.595. Finally, when both fixed year and firm effects are added to form the tenth regression, the GLM R2 increases to 0.613. However, the increment in R2 from adding fixed year and firm effects is far less here, 0.224 (=0.613- 0.389), than for the corresponding the conventional regressions, 0.516 (=0.594-0.078), confirming our suspicion that fixed effects largely capture differential investment propensities.
The results for the conventional and propensity regressions of R&D, shown in Panel B, are analogous. In particular, for the conventional regressions adjusted R2 increases dramatically (to 0.861 in the fifth regression from 0.119 in the second regression) as fixed year and firm effects are added, while for the propensity regressions GLM R2 increases much more modestly (to 0.875 in the tenth regression from 0.684 in the seventh regression).
In summary, the results in Table 4 provide strong support for propensity modeling and regression methodology as applied to both capital expenditures and R&D. Results also indicate that financial constraints affect both capital expenditure and R&D investment.
Propensity regressions for subsamples
Next we estimate propensity regressions for subsamples by Economy, firm size/age, and combinations thereof. For all regressions, the dependent variable is either capital expenditures or R&D investment, explicit regressors include (weighted) Qt-1 and NCFt/TA’t-1, and fixed year and firm effects are also included. Our main purpose for this subsample analysis is to gauge the rubustness of the coefficient of (weighted) Qt-1.In addition, though, the subsample analyses allow us to test two hypotheses regarding the effect of financial constraints on investment. First, Hadlock and Pierce suggest that mixed results in previous studies may be due to problems in measuring financial constraint. Their results indicate that firm size and age are effective measures of constraint (i.e., small and young firms are more likely to be financially constrained). However, in capital expenditure regressions they find that ICF sensitivity is not consistently related to their size/age index. If small/young firms are indeed more financially constrained, then the coefficient of NCFt/TA’t-1 should be higher for these firms than for large/mature firms.
Second, Brown, Fazzari, and Petersen [45], Brown and Petersen [25], and others argue that developments in the U.S. equity markets over time (particularly, over the time span covered by our study) have fostered a reduction in financial constraints over time for firms in general. Included in these developments are improvements in corporate governance, such as mechanisms to curb managers’ penchant for ‘empire building [46-48]. If so, then the coefficient of NCFt/TA’t-1 should be lower using New Economy subsamples vs. Old Economy subsamples.
Results are shown in Table 5 Panels A and B for capital expenditures and R&D, respectively. Note initially that in both panels results are fairly consistent across the subsamples: In every regression the coefficients of pwt-1*Qt-1 and pwt-1*NCFt/TA’t-1 are reliably positive, and the GLM R2s are fairly stable at high levels. Thus, the results are broadly robust [49-55].
| Sample | Firm | pwt-1* | GLMR2 | ||
|---|---|---|---|---|---|
| period | period | N | Qt-1 | NCFt/TA't-1 | |
| PanelA:Dep.var.= CAPXt/TA't-1; pwt=PPENTt-1/TA't-1 | |||||
| Allfirm/years | All | 94,056 | 0.047*** | 0.448*** | 0.613 |
| OldEconomy | All | 29,720 | 0.040*** | 0.642*** | 0.609 |
| New Economy | All | 64,336 | 0.048*** | 0.332*** | 0.653 |
| OldEconomy | Large/mature | 25,873 | 0.045*** | 0.688*** | 0.627 |
| OldEconomy | Small/young | 3,847 | 0.018*** | 0.373*** | 0.694 |
| New Economy | Large/mature | 52,235 | 0.049*** | 0.342*** | 0.671 |
| New Economy | Small/young | 12,101 | 0.043*** | 0.229*** | 0.779 |
| PanelB: Dep.var.=R&Dt/TA't-1; pwt=R& DCAPt-1/TA't-1 | |||||
| All firm/years | All | 94,056 | 0.037*** | 0.403*** | 0.875 |
| Old Economy | All | 29,720 | 0.035*** | 0.486*** | 0.923 |
| New Economy | All | 64,336 | 0.034*** | 0.382*** | 0.873 |
| Old Economy | Large/mature | 25,873 | 0.038*** | 0.628*** | 0.933 |
| Old Economy | Small/young | 3,847 | 0.027*** | 0.308*** | 0.943 |
| New Economy | Large/mature | 52,235 | 0.034*** | 0.410*** | 0.881 |
| New Economy | Small/young | 12,101 | 0.028*** | 0.244*** | 0.935 |
Notes: Results of propensity regressions of capital expenditures (Panel A) and R&D (Panel B) on Tobin’s Q (Qt-1) and operating net cash flow (NCFt/TA't-1). Propensity weight is pwt-1. Fixed year and firm effects are included. Results are for indicated combinations of sample period (Old vs. New Economy years, 1974- 87 vs. 1988-2008) and large/mature vs. small/young firms. Signifi`cance indicators: *** (1%); ** (5%); * (10%).
Table 5: Propensity Regressions of Capital Expenditures and R&D by Economy and Firm Size/Age
In Panel A, results are consistent with the equity-market development hypothesis in that the coefficient of pwt-1*NCFt/TA’t-1 is lower for New Economy subsamples than Old Economy subsamples. However, the results are not consistent with the hypothesis that small/ young firms are more financially constrained, as the coefficient of pwt-1*NCFt/TA’t-1 is substantially higher for large/mature firms than for small/young firms. Similarly, results in Panel B are (a) consistent with the equity-market development hypothesis in that the coefficient of pwt-1*NCFt/TA’t-1 is lower for New Economy subsamples than Old Economy subsamples, but (b) inconsistent with the hypothesis that small/young firms are more financially constrained, as the coefficient of pwt-1*NCFt/TA’t-1 is substantially higher for large/mature firms than for small/young firms.
Additional evidence on the equity-market development hypothesis
For the final analysis in this section, we draw together two important results documented earlier. First, Figure 1 shows that R&D investment by U.S. firms has generally increased over time. Second, results in Table 5 Panel B indicate that equity-market developments in the U.S. over time have served to lower financial constraints on R&D investment. If the latter directly influenced the former, then we should find that IP-intensive firms, particularly small/young IP-intensive firms, had better access to external equity capital to finance R&D in the New Economy than in the Old Economy. To test this conjecture, we focus on IP-intensive firms; i.e., firms for which R&DCAPt-1/TA’t- 1>0.10. We sort these firms by Economy and firm size/age, and then calculate and compare average values of relevant variables.
Results, shown in Table 6, are consistent with our conjecture. First, average R&D investment increased significantly from the Old to the New Economy for both large/mature firms and small/young firms (while average capital expenditure investment decreased, as shown). Second, this increase in R&D occurred despite the evidence that average operating net cash flow (NCFt/TA’t-1) decreased from the Old to the New Economy for both classes of firms. Third, net debt financing does not appear to contribute marginally to the external financing of R&D because average NETDTt/TA’t-1 is actually insignificantly lower in the New vs. Old Economy for both classes of firms. Instead, and fourth, net equity financing help to finance the increases in R&D investment, as average NETEQt/TA’t-1 is significantly higher in the New vs. Old Economy for both classes of firms.
| OldEconomy | NewEconomy | Diff.Newvs. Old | ||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Lg./MatureSm./Young | Diff. | Lg./MatureSm./Young | Diff. | Lg./MatureSm./Young | |||
| CAPXt/TA't-1 | 0.076 | 0.068 | 0.007*** | 0.041 | 0.034 | 0.007*** | -0.034*** | -0.034*** |
| R&Dt/TA't-1 | 0.074 | 0.093 | -0.019*** | 0.101 | 0.122 | -0.021*** | 0.027*** | 0.029*** |
| NCFt/TA't-1 | 0.159 | 0.124 | 0.035*** | 0.124 | 0.072 | 0.052*** | -0.035*** | -0.052*** |
| NETDTt/TA't-1 | 0.013 | 0.010 | 0.003 | 0.011 | 0.009 | 0.002 | -0.002 | -0.001 |
| NETEQt/TA't-1 | 0.023 | 0.050 | -0.027*** | 0.043 | 0.087 | -0.044*** | 0.020*** | 0.037*** |
| Qt-1 | 1.576 | 1.927 | -0.350*** | 2.231 | 2.111 | 0.120*** | 0.655*** | 0.185*** |
| N | 3,128 | 804 | 14,386 | 4,102 | ||||
Notes: Old (New) Economy years are 1974-87 (1988-2008). IP-intensive firms are defined by R&DCAPt-1/TA't-1 > 0.10.
Table 6: Averages of R&D and Related Variables for IP-Intensive Firms by Size/Age in Old and New Economies
In this section we analyze corporate investment and its determinants for individual industries, which can shed additional light on both inter temporal dynamics and cross-sectional variation documented thus far for all firms. We use the five industries given on Ken French’s website, defined there by ranges of SIC code values: High-tech; Healthcare; Consumer; Manufacturing and Energy; and Other.
Time series average values of investment and related variables by industry
For initial perspective on the investment patterns in each industry, we calculate annual average values of PPENTt-1/TA’t, R&DCAPt-1/TA’t, CAPXt/TA’t-1, R&Dt/TA’t-1, and Qt-1 for each industry. The results are displayed in Figures 2a-e. For all industries, average Qt-1 generally increases over time. Based on trends in the other variables, we can readily sort the industries into two groups. Group 1 consists of the High-Tech and Healthcare industries, for which average values of PPENTt/TA’t and CAPXt/TA’t-1 (R&DCAPt/TA’t and R&Dt/TA’t-1) have decreased (increased) substantially over time. That is, firms in the group 1 industries generally have evolved substantially from a physical-capital orientation to an IP orientation. Group 2 consists of the Consumer and Manufacturing & Energy industries. For this group, average values of PPENTt/TA’t and CAPXt/TA’t-1 are fairly stable at high levels over time, while average values of R&DCAPt/TA’t and R&Dt/TA’t-1 are fairly stable at very low levels. Average values for the ‘Other’ industry classification exhibit trends that lie between the extremes of these two groups.
The evidence in the figures suggests that, across industries, firms have pursued alternative types of investment in order to increase Q. For firms in industry group 1, value enhancement required evolving away from physical investment and toward IP investment. For firms in industry group 2, value enhancement apparently involved more efficient capital expenditure investment, perhaps facilitated by improvements in corporate governance. Next, we use propensity regressions to test these conjectures.
Propensity regressions by industry
As before, our propensity regressions include pwt-1*Qt-1 and pwt- 1*NCFt/TA’t-1 as well as fixed year and firm effects. We initially estimate propensity regressions using all firm-year observations in each industry. We then sort observations in each industry by Economy and combinations osf Economy and firm size/age, and estimate regressions for each resulting subsample. The results are shown in Tables 7 and 8 for capital expenditures and R&D, respectively. In each table, results for the High-tech, Healthcare, Consumer, Manufacturing & Energy, and Other industries are shown in Panels A-E, respectively.
| Sample | Firm | pwt-1* | GLM R2 | ||
|---|---|---|---|---|---|
| Period | Size/Age | N | Qt-1 | NCFt/TA't-1 | |
| PanelA:High-tech | |||||
| Allyears | All | 18,236 | 0.055*** | 0.446*** | 0.594 |
| OldEconomy | All | 3,773 | 0.041*** | 0.704*** | 0.608 |
| NewEconomy | All | 14,463 | 0.051*** | 0.308*** | 0.620 |
| OldEconomy | Large/Mature | 2,949 | 0.067*** | 0.739*** | 0.666 |
| OldEconomy | Small/Young | 824 | 0.011 | 0.270* | 0.673 |
| NewEconomy | Large/Mature | 11,410 | 0.053*** | 0.315*** | 0.630 |
| NewEconomy | Small/Young | 3,053 | 0.067*** | 0.152*** | 0.809 |
| Panel B:Healthcare | |||||
| Allyears | All | 8,287 | 0.041*** | 0.348*** | 0.483 |
| OldEconomy | All | 1,304 | 0.058*** | 0.350*** | 0.549 |
| NewEconomy | All | 6,983 | 0.036*** | 0.295*** | 0.466 |
| OldEconomy | Large/Mature | 1,023 | 0.062*** | 0.454*** | 0.565 |
| OldEconomy | Small/Young | 281 | 0.042 | 0.482* | 0.672 |
| NewEconomy | Large/Mature | 5,397 | 0.045*** | 0.231*** | 0.498 |
| NewEconomy | Small/Young | 1,586 | 0.009 | 0.255*** | 0.678 |
| Panel C: Consumer | |||||
| Allyears | All | 24,727 | 0.050*** | 0.365*** | 0.595 |
| OldEconomy | All | 8,999 | 0.042*** | 0.674*** | 0.609 |
| NewEconomy | All | 15,728 | 0.056*** | 0.225*** | 0.636 |
| OldEconomy | Large/Mature | 8,072 | 0.040*** | 0.688*** | 0.625 |
| OldEconomy | Small/Young | 927 | 0.060*** | 0.234*** | 0.739 |
| NewEconomy | Large/Mature | 12,918 | 0.054*** | 0.231*** | 0.661 |
| NewEconomy | Small/Young | 2,810 | 0.048*** | 0.195*** | 0.740 |
| Panel D:Manufacturing&Energy | |||||
| Allyears | All | 23,735 | 0.042*** | 0.514*** | 0.652 |
| OldEconomy | All | 9,749 | 0.035*** | 0.640*** | 0.621 |
| NewEconomy | All | 13,986 | 0.045*** | 0.427*** | 0.706 |
| OldEconomy | Large/Mature | 8,783 | 0.044*** | 0.654*** | 0.636 |
| OldEconomy | Small/Young | 966 | 0.008 | 0.509*** | 0.659 |
| NewEconomy | Large/Mature | 12,190 | 0.043*** | 0.435*** | 0.714 |
| NewEconomy | Small/Young | 1,796 | 0.048*** | 0.320*** | 0.808 |
| Panel E:Other | |||||
| Allyears | All | 19,071 | 0.043*** | 0.415*** | 0.593 |
| OldEconomy | All | 5,895 | 0.035*** | 0.598*** | 0.603 |
| NewEconomy | All | 13,176 | 0.043*** | 0.288*** | 0.626 |
| OldEconomy | Large/Mature | 5,046 | 0.033*** | 0.696*** | 0.613 |
| OldEconomy | Small/Young | 849 | 0.011 | 0.295*** | 0.720 |
| NewEconomy | Large/Mature | 10,320 | 0.045*** | 0.319*** | 0.651 |
| NewEconomy | Small/Young | 2,856 | 0.030*** | 0.143*** | 0.773 |
Notes: pwt-1=PPENTt-1/TA't-1. Significance indicators: *** (1%); ** (5%); * (10%).
Table 7: Propensity Regressions of Capital Expenditures by Industry, Economy, and Firm Size/Age.
| Sample | Firm | pwt-1* | GLM R2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Period | Size/Age | N | Qt-1 | NCFt/TA't-1 | ||||||
| PanelA:High-tech | ||||||||||
| Panel A: High-Tech Allyears | All | 18,236 | 0.040*** | 0.385*** | 0.812 | |||||
| OldEconomy | All | 3,773 | 0.041*** | 0.554*** | 0.888 | |||||
| NewEconomy | All | 14,463 | 0.038*** | 0.357*** | 0.810 | |||||
| OldEconomy | Large/Mature | 2,949 | 0.026*** | 0.662*** | 0.901 | |||||
| OldEconomy | Small/Young | 824 | 0.051*** | 0.525*** | 0.921 | |||||
| NewEconomy | Large/Mature | 11,410 | 0.037*** | 0.405*** | 0.823 | |||||
| NewEconomy | Small/Young | 3,053 | 0.024*** | 0.196*** | 0.902 | |||||
| PanelB:Healthcare | ||||||||||
| Allyears | All | 8,287 | 0.032*** | 0.363*** | 0.823 | |||||
| OldEconomy | All | 1,304 | 0.031*** | 0.303*** | 0.916 | |||||
| NewEconomy | All | 6,983 | 0.030*** | 0.363*** | 0.817 | |||||
| OldEconomy | Large/Mature | 1,023 | 0.030*** | 0.724*** | 0.939 | |||||
| OldEconomy | Small/Young | 281 | 0.032*** | -0.018 | 0.960 | |||||
| NewEconomy | Large/Mature | 5,397 | 0.031*** | 0.362*** | 0.824 | |||||
| NewEconomy | Small/Young | 1,586 | 0.035*** | 0.291*** | 0.916 | |||||
| PanelC:Consumer | ||||||||||
| Allyears | All | 24,727 | 0.045*** | 0.260*** | 0.858 | |||||
| OldEconomy | All | 8,999 | 0.041*** | 0.362*** | 0.907 | |||||
| NewEconomy | All | 15,728 | 0.039*** | 0.215*** | 0.861 | |||||
| OldEconomy | Large/Mature | 8,072 | 0.061*** | 0.607*** | 0.930 | |||||
| OldEconomy | Small/Young | 927 | -0.083*** | 0.325*** | 0.933 | |||||
| NewEconomy | Large/Mature | 12,918 | 0.046*** | 0.233*** | 0.876 | |||||
| NewEconomy | Small/Young | 2,810 | 0.026*** | 0.042 | 0.929 | |||||
| PanelD:Manufacturing&Energy | ||||||||||
| Allyears | All | 23,735 | 0.041*** | 0.516*** | 0.853 | |||||
| OldEconomy | All | 9,749 | 0.049*** | 0.634*** | 0.903 | |||||
| NewEconomy | All | 13,986 | 0.036*** | 0.446*** | 0.854 | |||||
| OldEconomy | Large/Mature | 8,783 | 0.056*** | 0.741*** | 0.910 | |||||
| OldEconomy | Small/Young | 966 | -0.037*** | 0.175*** | 0.911 | |||||
| NewEconomy | Large/Mature | 12,190 | 0.036*** | 0.435*** | 0.854 | |||||
| NewEconomy | Small/Young | 1,796 | 0.033*** | 0.119*** | 0.942 | |||||
| PanelE:Other | ||||||||||
| Allyears | All | 19,071 | 0.039*** | 0.521*** | 0.884 | |||||
| OldEconomy | All | 5,895 | 0.026*** | 0.385*** | 0.917 | |||||
| NewEconomy | All | 13,176 | 0.038*** | 0.501*** | 0.889 | |||||
| OldEconomy | Large/Mature | 5,046 | 0.043*** | 0.349*** | 0.926 | |||||
| OldEconomy | Small/Young | 849 | 0.010 | 0.386*** | 0.943 | |||||
| NewEconomy | Large/Mature | 10,320 | 0.038*** | 0.581*** | 0.899 | |||||
| NewEconomy | Small/Young | 2,856 | 0.019*** | 0.395*** | 0.935 | |||||
Notes: pwt-1=PPENTt-1/TA't-1. Significance indicators: *** (1%); ** (5%); * (10%).
Table 8: Propensity Regressions of R&D by Industry, Economy, and Firm Size/Age.
Before we turn to the propensity regression results, we point out that the two industry groups defined earlier differ not only in terms of their investment propensities, but also by each of two measures of growth. The first measure is Qt-1, interpreted as a measure of ex ante growth expectations. As Figure 2a-e shows, in both Economies average Qt-1 is consistently higher for industries in group 1 than group 2. The second growth measure is ex post; the percentage change in the number of firm-year observations from the Old Economy to the New. Using the values of ‘N’ shown in Tables 7 and 8, the percentage change in firmyear observations from the Old Economy to the New is substantially higher for industries in group 1 (283.3% and 435.5% for High-Tech and Healthcare, resp.) than in group 2 (74.8% and 43.5% for Consumer and Manuf. and Energy, resp.). These results, in combination with earlier results, indirectly suggest that equity-market developments produced value and growth in the group 1 industries, while for the group 2 industries value may have been created more by impeding inefficient growth (i.e., empire building) through enhancements in corporate governance.
Turning to the propensity regression results, we note initially that the overall results in Tables 7 and 8 attest to the robustness of propensity regression methodology. Across the numerous subsamples, with only rare exceptions the coefficients of pwt-1*Qt-1 and pwt-1*NCFt/ TA’t-1 are reliably positive and the GLM R2 statistic is very high.
In Table 7, for every industry the coefficient of pwt-1*NCFt/TA’t-1 falls substantially from the Old Economy to the New. If these results are driven by improvements in corporate governance over time, we should find that the coefficient of pwt-1*NCFt/TA’t-1 falls more substantially for large/mature firms than for small/young firms, because large/mature firms are more likely to exhibit empire building behavior in the Old Economy. For all industries except Healthcare, this is the case.
In Table 8, we focus only on results for the High-Tech and Healthcare industries, where R&D investment has been consistently higher. For the High-Tech industry, the coefficient of pwt-1*NCFt/TA’t-1 falls from the Old Economy to the New for all firms, and the decrease is especially large for small/young firms. These results suggest that equitymarket developments have been especially helpful for small/young firms in this industry. For the Healthcare industry, the coefficient of pwt-1*NCFt/TA’t-1 actually rises slightly from the Old Economy (0.303) to the New Economy (0.363) for all firms. However, the coefficient falls substantially for large/mature firms in the industry (from 0.724 to 0.362) and rises for small/young firms in the industry (from an insignificant -0.018 to 0.291). However, the latter results must be interpreted with caution because of the relative dearth of observations for small/young firms in the Healthcare industry in the Old Economy (only 281 firm- year observations). In conclusion, the results are mixed but generally consistent with the hypothesis that equity-market developments have enhanced the ability of IP-intensive firms to pursue R&D investment to create value.
This paper develops and tests modified q models that account for individual firms’ propensities to make physical vs. IP investment. Results of empirical tests of these models, facilitated with propensity regression methodology, provide strong support for q theory and are robust to subsample scrutiny. We also document evidence that financial constraints affect investment, though developments in U.S. equity markets over time appear to have alleviated these constraints substantially, for both capital expenditure and R&D investment. Finally, we find that R&D investment has been consistently higher and growing for firms in the High-Tech and Healthcare industries, while for firms in Consumer and Manufacturer and Energy capital expenditure investment is relatively more important.
For their helpful comments, we thaNK Bruce Petersen, Richard Smith, Tracy Wang, Neng Wang, Lingling Wang, and seminar participants at the University at Buffalo, the University of Kansas, McMaster University, the 2007 and 2010 FMA meetings, the 2010 FMA European meetings, and the 2011 American Economic Association meeting, where earlier drafts of this paper were presented. This paper is based on Wu’s dissertation completed at the University at Buffalo. Ogden acknowledges support from a UB SOM Summer Research grant.
1 For alternative q models of investment that allow for multiple types of investment, see Hayashi and Inoue [49], Chirinko [50], and Bond and Cummins [51]
2 Equations parallel to (15), (16), and (17) can be developed for the alternative case of estimating the true sensitivity of IP investment to Q given that the full sample consists of subsamples of physical- and IP-oriented firms
3These studies include: Fazzari, et al. [4]; Whited; Lang, et al. [20]; Kaplan and Zingales [21]; Erickson and Whited [18]; Bhagat, et al. (2005); Almeida and Campello [23]; Agca and Mozumdar [24]; and Hovakimian [52].
4 See Fazzari et al. [4]; Blundell et al. [6]; Gilchrist and Himmelberg [7]; Kaplan and Zingales [21]; Cleary [53]; Erickson and Whited [18]; Gomes [8]; Lamont et al. [54]; Almeida and Campello [23]; and Hadlock and Pierce [55].