Journal of Physical Chemistry & Biophysics
Open Access

Coupled Dufour and Soret Effects on Hybrid Nanofluid Flow through Gyrating Channel Subject to Chemically Reactive Arrhenius Activation Energy

Author info »

Introduction

In the earlier times the transfer of mass and heat has appealed the interest of research community with more significance for its important applications at industrial level. Some of these applications are electronic devises in the field of engineering, compact thermal exchangers and nuclear reactors etc. In the combined mass and heat transfer progressions the fluid flow is occurred due to variations in density resulted by gradient in concentration, temperature and composition of material. The transmission of mass is caused by variation in the thermal behavior of fluid particles which is termed as Soret effect. The energy’s flux occurred due to variations in concentration and termed as Dufour effect. It is of worth mentioning that these effects are of more importance for transmission of mass and heat in different engineering processes. Both Dufour and Soret effects become more significant whenever some species are acquaint at the surface of fluid with density smaller than that of surrounding fluid. Numerous applications of Soret and Dufour effects can be seen in the field of combustion flames, safety reactor, solar collectors and building energy conservations. Chamkha AJ, et al. [1], investigated MHD fluid flow upon a porous semi-infinite isothermal sheet with Soret and Dufour effects. Rasool G, et al. [2], revealed the impact of Soret and Dufour effect upon nanofluid flow with Darcy-Forchheimer terms in the mathematical model. It has concluded that the flow of nanoparticles has declined with higher values of porosity parameter. Khan, et al. [3], has introduced the Soret and Dufour effects with significant characteristics to viscous MHD fluid flow through a rotary cone by discussing its generation of entropy as well. Vafie, et al. [4], have inspected about the MHD and Dufour, Sorret effects for fluid flow upon a stretching surface and have established that thermal flow rate has declined with upsurge in radiation and viscous dissipation effects. Khan, et al. [5], have concluded about the flow of viscous fluid with combined influence of Soret and Dufour. The authors in this study have focused mainly upon the flow of heat mechanism and established that magnetic effects has upsurge the thermal flow rate. The thermal fluid flow for Casson fluid with ethylene glycol as pure fluid has inspected with impacts of Soret and Dufour effects by Hafeez, et al. [6]. Layek, et al. [7], deliberated the collective influence of Soret and Dufour on time-dependent mass and heat transfer over permeable surface. Kotnurkar, et al. [8], have discussed the characteristics of nanofluid flow with Soret and Dufour effects.

The combination of small sized particles in a base fluid for enhancement of its thermal flow characteristics is termed as nanofluid. The nanoparticles flow analysis has been the topic of widespread research for various investigators, as it has upgraded the thermal characteristics of thermal flow phenomena. The nanoparticles are composed of various metal oxides such as (CuO, Al₂O₃), metals such as (Cu, Au, Ag), semiconductors such as (Tio₂, SiC), nitride ceramics such as (AlN, SiN) and carbide ceramics such as (SiC, TiC). The idea of suspending nanoparticles into a base fluid was first drifted by Choi, et al. [9]. This work has provided a new base in the field of fluid mechanics. For its significant applications in the field of engineering and at industrial level various studies have been carried out with main focus upon thermal diffusivity amongst the nanoparticles. Sheikholeslami, et al. [10], inspected the nanofluid flow with thermal transmission through a gyrating channel by implementing the magnetic effects. It has concluded in this inspection that there has been a direct relationship between nanoparticles volume fraction and Nusselt number for both injection and suction cases. Zangooee, et al. [11], have explored the flow of nanoparticles with squeezing effects through two spinning plates. Abbas, et al. [12], examined the irreversibility generation for MHD nanofluid flow with second order velocity slip condition. The fluid in this study has also accompanied by nonlinear mixed convection, thermal radiation and thermal dissipation. Hatami, et al. [13], have used the divergent wavy channel for fluid flow with thermal transmission and have used Galerkin finite difference technique for solution of modeled equations.

With the passage of time researchers have realized that the dispersion of two dissimilar kinds of nanoparticles in a pure fluid results in a fluid that has higher thermal diffusion. This new class of fluid is called as hybrid nanofluid. Islam, et al. [14], deliberated the effects of Hall current for radiated hybrid nanofluid flow through a channel and have concluded that hybrid nanolfuid have superior thermal flow characteristics than traditional fluid. Khan, et al. [15], inspected the irreversibility generation for hybrid nanofluid through revolving plates. Li, et al. [16], deliberated the creation of entropy for hybrid nanofluid between two plates by considering the effects of Marangoni convection in the flow model with other flow conditions. It has concluded in this work that, rate of flow transmission is at peak for greater values of exponential and thermal source sink. Ali, et al. [17], have inspected the hybrid nanofluid and hybrid nanomaterial with modified model of Buongiorno upon elongated sheet.

In a rotating system, the flow of fluid is a natural phenomenon. Actually, these effects of rotation occur internally among a fluid’s particles that augment when the fluid gets into motion. Hence in the fluid motion the natural rotation exists up to a specific range. The concept of rotating system in viscous fluid flow was floated by Taylor, [18]. The investigation of rotational motion for different flow system has been conducted in detail by Greenspan, [19]. The idea of rotational motion has also extended to moving disks [20]. Forbes, [21], has investigated the axisymmetric flow of fluid between two plates with lower plate as static and the upper plate as rotational. Dongonchi, et al. [22], inspected the influence of stretching of surface upon nanofluid flow and heat conduction in rotary channel. Muhammad, et al. [23], have inspected the squeezing fluid flow between rotational plates. In this work the effects of MHD has also taken into account for flow system. Salahuddin, et al. [24], have picked second grade fluid motion through rotary plates by considering variable fluid characteristics. It has proved in this study that diffusivity and concentration of fluid particles are related directly with thermal conductivity and thermal transmission.

The least energy required by molecules for commencement of a chemical reaction is termed as activation energy introduced by Arrhenius. Activation energy has many applications in processing of food, and emulsions of different suspensions. First result in the paper format with combine impact of activation energy was established by Bestman, [25]. Khan, et al. [26], have inspected the influence of Arrhenius activation energy upon MHD second grade fluid flow in a permeable surface. The term has been also used by Bhatti, et al. [27], by considering its impact upon thermos-bioconvective nanofluid flow over a Riga plate and have concluded that flow profiles have been weakened by expanding values of Rayleigh number. Khan, et al. [28], have deliberated a wonderful work upon hybrid nanofluid flow by considering the influence of Arrhenius activation energy upon flow system. The authors have concluded in their investigation that mass diffusivity has jumped up for expansion in activation energy parameter. More established work can be studied [29-33].

The effects of magnetic field have a considerable part in fluid mechanics. It has numerous engineering and industrial applications for instance MHD generators and pumps etc. Various investigations have been conducted with main emphasis upon transportation of heat with MHD effects. Shehzad, et al. [34], have inspected the influence of MHD upon three dimensional flow of Jeffery fluid with Newtonian heating effects and have revealed that fluid’s motion has opposed while the thermal flow rate and skin friction have supported with augmentation in magnetic parameter. Makinde, et al. [35], have inspected numerically the impact of MHD upon Cuoette flow in generalized form with variable thermal conductance and viscosity and have concluded that the electrical and hydromagnetic properties of fluid flow have greatly influenced by magnetic and viscosity parameters. Usman, et al. [36], have investigated the EMHD impact upon couple stress film flow of nanofluid over spinning disk and have calculated the percentage augmentation in thermal flow rate for single and double nanoparticles fluid flow. Bejawada, et al. [37], have studied radiated MHD Casson fluid flow over inclined nonlinear surface with influence of Darcy Forchheimer effects. Mogharrebi, et al. [38], have inspected the rotational flow with MHD and microbes influence and have revealed that for a variation in magnetic field from 0 to 1 the thermal flow rate has reduced by 3.11%.

Form the aforementioned investigations it has discovered that no study has yet been steered to deliberate the thermal flow rate for hybrid nanofluid flow through rotating plates by employing the combined Dufour, Soret effects and the impact of microorganisms. The following points support the novelty of the work.

• Coupled Dufour and Soret effects are taken in mathematical model of flow problem.

• Chemically reactive Arrhenius activation energy is also incorporated in concentration equation.

• The plates at the boundaries are considered as rotating, where the spinning effects of plates are coupled in the flow equations.

• The effects of microorganism has used in the modeled equations.

• Magnetic effect is applied to the flow system and is incorporated mathematically in momentum equations.

• HAM is worked out for solution of model problem.

Materials and Methods

Problem formulation

Take an incompressible viscous hybrid nanofluid fluid flow between two plates. The system of coordinates is selected so that plates along with fluid are rotating with angular velocity Ω about y-axis. h is the distance between the plates such that Cu, Al₂O₃-nanoparticles are mixed with water for formulating hybrid nanofluid with combination (Cu+Al₂O₃+H₂O). The flow is influenced by the coupled effects of Dufour and Soret diffusions.

The collective impact of chemically reactive Arrhenius activation energy has incorporated in mathematical model of problem. Magnetic field has also employed to the flow system with strength B₀ in normal direction to the plates as depicted in Figure 1. It is supposed that the existence of nanoparticles will not affect the microorganisms’ direction, swimming and their velocity.

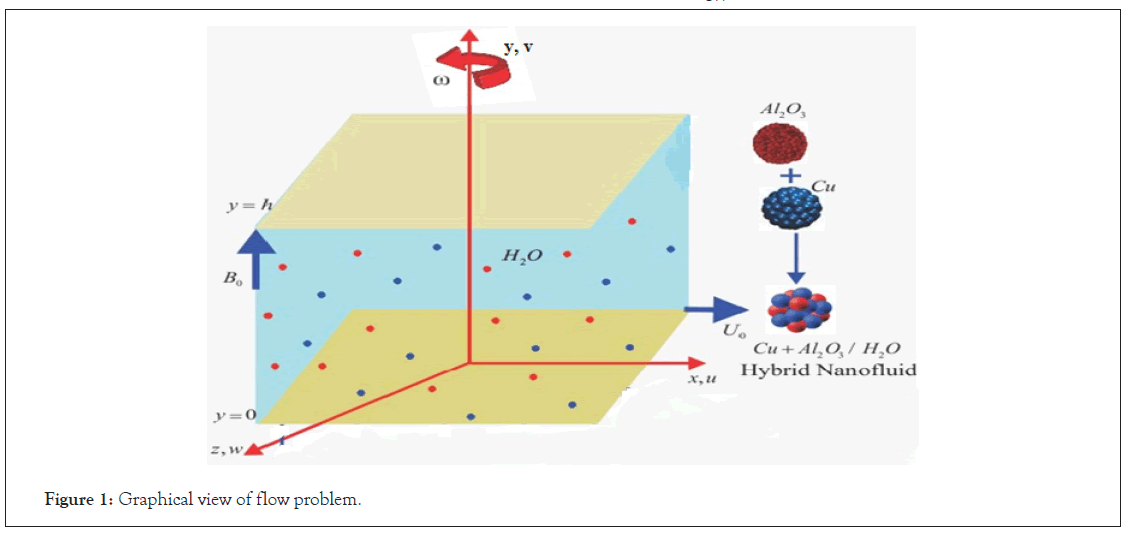
Figure 1: Graphical view of flow problem.

With the help of above assumptions one have following set of equations [14,39,40]

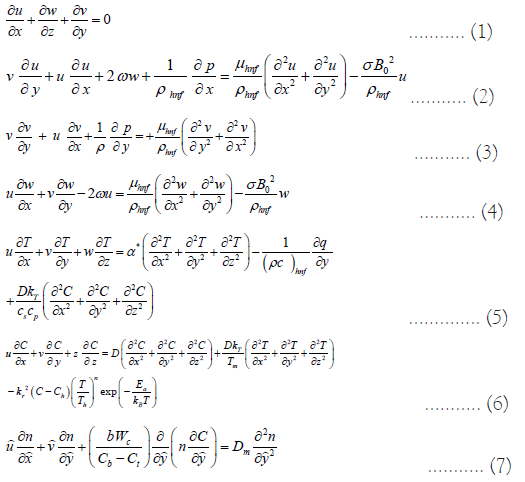
Above the flow components are respectively along coordinate axes, 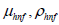are the dynamic viscosity and density of hybrid nanofluid, ω is the angular velocity, qr is the heat flux due to radiation, 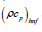is heat capacitance, 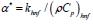is the thermal diffusion in which 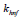is thermal conductance of nanofluid, D_M is mass diffusivity, kT is ratio of thermal diffusion, D_m is diffusion of microorganism, C₀,T₀ are the concentration and temperature at lower plate of channel while C_h,T_h are the corresponding quantities at the upper plate. Moreover, 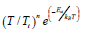is modified Arrhenius function, W_c is speed of microorganism cells, E_a is activation energy, and kr² is the rate of reaction.

Conditions at boundaries are

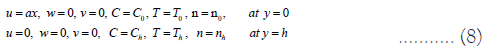
Use the following set of suitable transformations [41,42]

For simplification of q_r use the Rosseland approximation as given below.

In Equation (10) σ ^*, κ ^* are termed as Stefan Boltzmann constant and coefficient of Rosseland mean absorption such that . If the thermal gradient is sufficiently small within the flow of fluid then T⁴ can be simplified by using Taylor’s expansion.

In light of Equations (10,11) we have from Equation (6) as

In light of Equation (9) we have from Equations (1-4,6,7 and 12) in dimensionless form as follows

Above, Re is Reynolds number, Kr is rotation parameter, M is magnetic parameter, Pr is Prandtl number, Rd is radiation parameter, Du is Dufour number, E is activation energy parameter,τ is Temperature parameter, Sr is Soret number, Γ is chemical reaction parameter, Scis Schmidt number L_b, P_e are bio-convection Lewis and Peclet numbers. These parameters are mathematically described as:

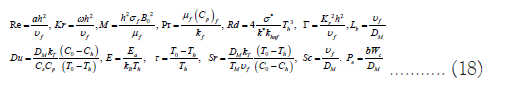
The thermos-physical characteristics of solid nanoparticles are defined as follows with its numerical values are depicted in Table 1.

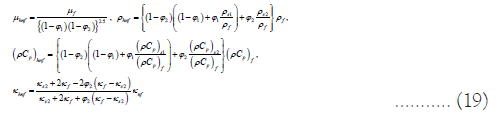
The related conditions at the boundaries are:

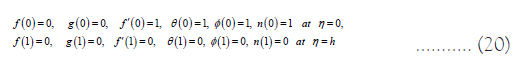
Physical quantities

In the problems related to thermodynamics, the engineers and scientists are normally interested to determine the thermal and mass flow rates for fluid flow system. In this regard some quantities of interest are depicted bellow:

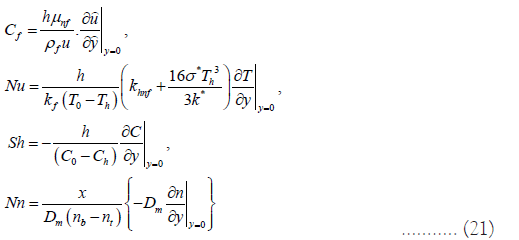
Incorporating Equation (9) in Equation (21), the resultant equations in refined form are expressed as:

Problem solution

For solution of modeled equations the semi-analytical technique HAM will be incorporated. This technique describes the solution in the form of functions and is most suitable for solving nonlinear equations. To solve Equations (13-17) by considering boundary conditions in Equation (20), we shall start with the following initial guesses:

Whereas the linear operators are described as

The relations in Equation (24) can be mathematically described as:

In Equation (25) di for i =1, 2,3.......9 are constants.

Results and Discussion

In this work an attempt is made to explore the characteristics of magnetohydrodynamic hybrid nanofluid flow through two rotating plates. The flow is influenced by the coupled effects of Dufour and Soret diffusion and motile microorganisms. Magnetic field has employed to the flow system with strength B₀ in normal direction to the plates. The system of equations is shifted to dimension-free format by using suitable variables. Various non-dimensional factors have been encountered in the process of non-dimensionalization which will be discussed in the forthcoming sections.In this work an attempt is made to explore the characteristics of magnetohydrodynamic hybrid nanofluid flow through two rotating plates. The flow is influenced by the coupled effects of Dufour and Soret diffusion and motile microorganisms. Magnetic field has employed to the flow system with strength B₀ in normal direction to the plates. The system of equations is shifted to dimension-free format by using suitable variables. Various non-dimensional factors have been encountered in the process of non-dimensionalization which will be discussed in the forthcoming sections.

Effects of emerging parameters f (η ) on g (η ) and profiles

In Figures 2a and 2b the effect of magnetic factor M upon f (η ) g (η ) and is portrayed. Clearly an expansion in M results the creation of Lorentz force in the fluid motion and offer more resistance to linear velocity. In this process swirling motion is

supported by Lorentz force. Hence the higher values M of decline f (η ) as depicted in Figure 2a and augment the profiles of g (η ) as presented in Figure 2b. The impact is more significant for hybrid nanoparticles than traditional nanoparticles. The influence of rotational parameter Kr upon f (η ) and g (η ) is depicted in Figure 3a and 3b. Since augmentation in Kr supports the rotational behavior and opposing linear behavior of fluid motion, hence higher values of Kr retards fluid motion f (η ) and augments g (η ) as portrayed in Figures 3a and 3b. From Figures 4a and 4b it has noticed that augmentation in volumetric fractions φ₁ ,φ₂ retarded the fluid motion linearly and rotationally. This phenomenon can be explained as with augmentation in φ₁ ,φ₂ the dense behavior of nanoparticles enhanced within the fluid motion due to which more constraint is experienced by fluid motion. As a result the velocity profiles are declined in all directions. Since with higher values of Re the viscous forces become dominant due to which fluid motion tend to condense. Hence the linear as well as microrational velocity profiles retarded for growth in Re as depicted in Figures 5a and 5b.

Figure 2: Linear and micro-rotation velocities vs. variations in M. Note: Cu+Al₂O₃, Al₂O₃.

Figure 3: Linear and micro-rotation velocities vs. variations in Kr. Note: Cu+Al₂O₃, Al₂O₃.

Figure 4: Linear and micro-rotation velocities vs. variations in φ₁ , φ₂ . Note: Cu+Al₂O₃, Al₂O₃.

Figure 5: Linear and micro-rotation velocities vs. variations in Re. Note: Cu+Al₂O₃, Al₂O₃.

Effects of different emerging parameters on temperature profiles θ (η )

The influence of different emerging factors upon thermal profiles has portrayed in Figures 6a-6c. The growing values of Dufour number Du results an augmentation in thermal flow of fluid. Actually for higher values of Du, maximum energy transfer takes place from higher to lower concentration zone, hence causes a growth in thermal profiles as illustrated in Figure 6a.

Figure 6: Variations in temperature vs. variations in Du, φ₁ , φ₂ , Rd. Note: 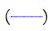Cu+Al₂O₃, 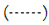Al₂O₃.

The higher values of φ₁ , φ₂ are responsible for generation of more friction to fluid flow in response of resistance to fluid motion. In this process kinetic energy of fluid particles converted to heat energy that overshoot the thermal flow of fluid as portrayed in Figure 6b. Figure 6c shows that augmentation in radiation factor Rd is responsible for growth in temperature. Actually, for higher values Rd of the thickness of thermal boundary layer grows up due to more transportation of heat that augments the thermal profiles.

Effects of different emerging parameters on concentration profiles Φ(η )

The influences of various emerging parameters upon concentration profiles have been depicted in Figures 7a-7c. Since the Soret number is mathematically expressed as 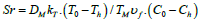so with upsurge in the Sr values of the concentration gradient of the fluid flow system will decline due to which less mass diffusivity will occur. In this process the concentration of the flow system retards as depicted in Figure 7a. It has perceived from Figure 7b that higher values of activation energy factor E supports the mass diffusion. Physically, it can be explained as a growth in the values of E shoot-up the concentration of molecules with less requisite energy and causes more transportation of mass for fluid flow system that ultimately strengthen the thickness of boundary layer for concentration. In this phenomenon concentration profiles upsurge as depicted in Figure 7b. The higher values of chemical reaction factor Γ drop the mass diffusion as illustrated in Figure 7c. Actually, with upsurge in Γ the chemical molecular diffusion decline due to which less diffusion of mass occurs and ultimately retards the concentration profiles.

Figure 7: Variations in concentration vs. variations in Sr, E, Γ . Note: 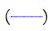Cu+Al₂O₃, 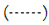Al₂O₃.

Effects of different emerging parameters on microorganism profiles χ (η )

The influence of bioconvection-Lewis and Pellet numbers (L_b, P_e) over microorganism profiles is illustrated in Figures 8a and 8b. The augmenting values of both these two parameters weakens the boundary layer thickness of microorganisms due to which less mass diffusions of motile microorganism take place as portrayed in Figures 8a and 8b.

Figure 8: Variations in χ (η ) vs. variations in L_b, P_e. Note: 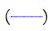Cu+Al₂O₃, 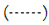Al₂O₃.

Table discussion

In Table 1 the thermophysical characteristics for different nanoparticles and base fluid have been depicted numerically. In Tables 2-5 the influence of different emerging parameters have been presented numerically upon various quantities of interest. Since magnetic factor, rotational and viscous parameters are responsible for resistance to fluid flow due to which maximum friction has experienced by fluid’s particles. Hence with growth in these three factors the skin friction grows up as depicted in Table 2. This impact is more visible for hybrid nanoparticles as compared to traditional or single nanoparticles. Table 3 depicts numerically the influence of magnetic, radiation factors and Dufour number. It is obvious from this table that Nusselt number has increased with growth in radiation parameter whereas upsurge in magnetic parameter and Dufour number has an adverse effect upon Nusselt number. Again the impact is more visible in case of hybrid nanofluid. Table 4 depicts that growing values of Schmidt number upsurge the Sherwood number whereas growing values of Dufour, Soret numbers and energy activation parameter has declined it. From Table 5 it has revealed that higher values of Lewis and Pellet numbers enhanced the motile rate.

Properties	Cu-nanoparticles	Al2O3-nanoparticles	H2O-base fluid
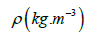	8933	3970	997.1
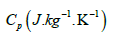	385	765	4179
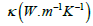	400	40	0.613.00

Table 1: Numerical values of bas fluid and nanoparticles for thermophysical characteristics.

Kr	M	Re	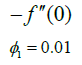Nanofluid	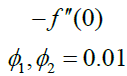Hybrid nanofluid	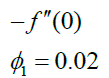Nanofluid	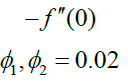Hybrid nanofluid
0.2	0.2	0.2	0.287654	0.327632	0.292109	0.335228
0.4			0.318745	0.345219	0.327659	0.354105
0.6			0.345683	0.3.6543456	0.353257	0.376427
	0.4		0.298211	0.312982	0.301298	0.320217
	0.6		0.308286	0.332878	0.317283	0.343213
		0.4	0.427654	0.467433	0.435428	0.475427
		0.6	0.632876	0.695423	0.645729	0.70252

Table 2: Influence of various parameters on skin friction coefficient 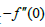at lower plate.

Rd	M	Du	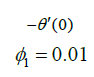Nanofluid	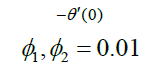Hybrid nanofluid	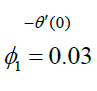Nanofluid	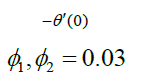Hybrid nanofluid
0.2	0.2	0.4	2.4621	2.520346	2.542146	2.632152
0.4			2.69821	2.74217	2.75327	2.852374
0.6			2.87321	2.942187	2.923187	3.103942
	0.4		2.673211	2.735673	2.772467	2.854736
	0.6		2.689213	2.701689	2.826892	2.896702
		0.6	2.21087	2.234211	2.323211	2.321234
		0.8	2.106592	2.141081	2.201066	2.210141

Table 3: Influence of nanofluid and hybrid nanofluid versus Nusselt number.

Sc	Sr	Du	E	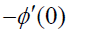Nanofluid	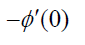Hybrid nanofluid
0.2	0.2	0.4	0.2	3.489254	3.489214
0.4				3.521975	3.521321
0.6				3.663219	3.663426
	0.4			3.532177	3.532285
	0.6			3.672383	3.672897
		0.6		3.552132	3.552321
		0.8		3.652201	3.652101
			0.4	3.362388	3.362439
			0.6	3.243187	3.243542

Table 4: Influence of nanofluid and hybrid nanofluid versus Sherwood number.

Lb	Pe	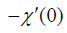Nanofluid	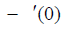Hybrid nanofluid
0.2	0.2	4.274489	4.274563
0.4		4.321522	4.321642
0.6		4.527663	4.527873
	0.4	4.432532	4.432643
	0.6	4.635672	4.635755

Table 5: Influence of nanofluid and hybrid nanofluid versus motile rate.

Conclusion

This study explores the MHD fluid flow through two rotating plates subject to effects of microorganism. The copper and alumina nanoparticles have been mixed with water for formulating hybrid nanofluid. This new combination augments the thermal conductivity of pure fluid. The flow is influenced by the coupled effects of Dufour and Soret diffusions. The joined effects of chemically reactive activation energy have been incorporated in the mass transportation equation. Magnetic effects have employed to the flow system with strength B₀ in normal direction to the plates. The impact of the embedded parameters has been examined theoretically by employing the graphical view of different flow profiles. After detail study of the article it has revealed that:

• Linear velocity has declined by augmentation in magnetic factor and rotational parameter whereas these factors have enhanced microrotational profiles of fluid.

• Augmentation in viscosity parameter and volumetric fractions has declined the fluid motion in all directions.

• Higher values of radiation parameter, Dufour number and volumetric fractions have augmented fluid’s thermal profiles.

• Concentration of fluid has retarded with upsurge in Soret number and chemical reaction parameter, whereas growth in activation factor of energy has supported the growth in concentration.

• Motility of microorganisms has retarded by upsurge in the values of bioconvection Lewis and Peclet numbers.

• Numerical influence of different factor upon various physical quantities of interest has evaluated for single and double nanoparticles. It has revealed that thermal flow rate has augmented more in case of hybrid nanofluid.

References

1. Chamkha AJ, Ben-Nakhi A. MHD mixed convection-radiation interaction along a permeable surface immersed in a porous medium in the presence of Soret and Dufour’s effects. Heat Mass Transf. 2008;44(7):845-856.

   [Crossref] [Google Scholar]

2. Rasool G, Shafiq A, Baleanu D. Consequences of Soret–Dufour effects, thermal radiation, and binary chemical reaction on Darcy Forchheimer flow of nanofluids. Symmetry. 2020;12(9):1421.

   [Crossref] [Google Scholar]

3. Khan SA, Hayat T, Khan MI, Alsaedi A. Salient features of Dufour and Soret effect in radiative MHD flow of viscous fluid by a rotating cone with entropy generation. Int J Hydrog Energy. 2020;45(28):14552-14564.

   [Crossref] [Google Scholar]

4. Vafai K, Khan AA, Fatima G, Sait SM, Ellahi R. Dufour, Soret and radiation effects with magnetic dipole on Powell-Eyring fluid flow over a stretching sheet. Int J Numer Method Heat Fluid Flow. 2021;31(4):1085-1103.

   [Crossref] [Google Scholar]

5. Khan SA, Hayat T, Alsaedi A. Irreversibility analysis in Darcy-Forchheimer flow of viscous fluid with Dufour and Soret effects via finite difference method. Case Stud Therm Eng. 2021;26:101065.

   [Crossref] [Google Scholar]

6. Hafeez MB, Sumelka W, Nazir U, Ahmad H, Askar S. Mechanism of solute and thermal characteristics in a casson hybrid nanofluid based with ethylene glycol influenced by Soret and Dufour effects. Energies. 2021;14(20):6818.

   [Crossref] [Google Scholar]

7. Layek GC, Mandal B, Bhattacharyya K. Dufour and Soret effects on unsteady heat and mass transfer for powell-eyring fluid flow over an expanding permeable sheet. J App Comput Mech. 2020;6(4):985-998.

   [Crossref] [Google Scholar]

8. Kotnurkar AS, Katagi DC. Thermo-diffusion and diffusion-thermo effects on MHD third-grade nanofluid flow driven by peristaltic transport. Arab J Sci Eng. 2020;45(6):4995-5008.

   [Crossref] [Google Scholar]

9. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. Argonne National Lab (ANL), Argonne, IL (United States). 1995.
10. Sheikholeslami M, Hatami M, Ganji DD. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J Mol Liq. 2014;190:112-120.

    [Crossref] [Google Scholar]

11. Zangooee MR, Hosseini SA, Ganji DD. Squeezing nanofluid flow between parallel rotating plates analysis by AGM method. Int J Ambient Energy. 2022;43(1):3322-3329.

    [Crossref] [Google Scholar]

12. Abbas SZ, Khan MI, Kadry S, Khan WA, Israr-Ur-Rehman M, Waqas M. Fully developed entropy optimized second order velocity slip MHD nanofluid flow with activation energy. Comput Methods and Programs Biomed. 2020;190:105362.

    [Crossref] [Google Scholar]

13. Hatami M, Sun L, Jing D, Günerhan H, Kameswaran PK. Rotating cylinder turbulator effect on the heat transfer of a‎ nanofluid flow in a wavy divergent channel‎. J Appl Comput Mech. 2021;7(4):1987-1998.

    [Crossref] [Google Scholar]

14. Islam S, Khan A, Deebani W, Bonyah E, Alreshidi NA, Shah Z. Influences of hall current and radiation on MHD micropolar non-Newtonian hybrid nanofluid flow between two surfaces. AIP Advances. 2020;10(5):055015.

    [Crossref] [Google Scholar]

15. Khan MI, Hafeez MU, Hayat T, Khan MI, Alsaedi A. Magneto rotating flow of hybrid nanofluid with entropy generation. Comput Methods Programs Biomed. 2020;183:105093. 

    [Crossref] [Google Scholar]

16. Li YX, Khan MI, Gowda RP, Ali A, Farooq S, Chu YM, et al. Dynamics of aluminum oxide and copper hybrid nanofluid in nonlinear mixed Marangoni convective flow with entropy generation: Applications to renewable energy. Chinese J Phys. 2021;73:275-287.

    [Crossref] [Google Scholar]

17. Ali B, Hussain S, Shafique M, Habib D, Rasool G. Analyzing the interaction of hybrid base liquid C2H6O2-H2O with hybrid nano-material Ag-MoS2 for unsteady rotational flow referred to an elongated surface using modified Buongiorno’s model: FEM simulation. Math Comput Simul. 2021;190:57-74.

    [Crossref] [Google Scholar]

18. Taylor GI. Experiments with rotating fluids. Proc R Soc London. Ser A Contain Pap Math Phys Character. 1921;100(703):114-121.

    [Crossref] [Google Scholar]

19. Greenspan HP. The theory of rotating fluids. CUP Archive. 1968.
20. Turkyilmazoglu M. Fluid flow and heat transfer over a rotating and vertically moving disk. Phys Fluids. 2018;30(6):063605.

    [Crossref] [Google Scholar]

21. Forbes LK. Steady flow of a Reiner-Rivlin fluid between rotating plates. Phys Fluids. 2018;30(10):103104.

    [Crossref] [Google Scholar]

22. Dogonchi AS, Ganji DD, Makinde OD. Impact of stretching and penetration of walls on nanofluid flow and heat transfer in a rotating system. In Defect and Diffusion Forum. Trans Tech Publications Ltd. 2018;387:37-50.

    [Crossref] [Google Scholar]

23. Muhammad S, Shah SI, Ali G, Ishaq M, Hussain SA, Ullah H. Squeezing nanofluid flow between two parallel plates under the influence of MHD and thermal radiation. Asian Res J Math. 2018;10(1):1-20.

    [Crossref] [Google Scholar]

24. Salahuddin T, Arshad M, Siddique N, Tlili I. Change in internal energy of viscoelastic fluid flow between two rotating parallel plates having variable fluid properties. Indian J Phys. 2021;95(9):1801-1811.

    [Crossref] [Google Scholar]

25. Bestman AR. Natural convection boundary layer with suction and mass transfer in a porous medium. Int J Energy Res. 1990;14(4):389-396.

    [Crossref] [Google Scholar]

26. Khan NS, Kumam P, Thounthong P. Second law analysis with effects of Arrhenius activation energy and binary chemical reaction on nanofluid flow. Sci Rep. 2020;10(1):1-6.

    [Crossref] [Google Scholar]

27. Bhatti MM, Michaelides EE. Study of Arrhenius activation energy on the thermo-bioconvection nanofluid flow over a Riga plate. J Thermal Anal Calorim. 2021;143:2029-2038.

    [Crossref] [Google Scholar]

28. Khan A, Saeed A, Tassaddiq A, Gul T, Mukhtar S, Kumam P, et al. Bio-convective micropolar nanofluid flow over thin moving needle subject to Arrhenius activation energy, viscous dissipation and binary chemical reaction. Case Stud Therm Eng. 2021;25:100989.

    [Crossref] [Google Scholar]

29. Muhammad T, Waqas H, Khan SA, Ellahi R, Sait SM. Significance of nonlinear thermal radiation in 3D Eyring-Powell nanofluid flow with Arrhenius activation energy. J Thermal Anal Calorim. 2021;143:929-944.

    [Crossref] [Google Scholar]

30. Asma M, Othman WA, Muhammad T. Numerical study for Darcy-Forchheimer flow of nanofluid due to a rotating disk with binary chemical reaction and Arrhenius activation energy. Mathematics. 2019;7(10):921.

    [Crossref] [Google Scholar]

31. Kumar R, Bhattacharyya A, Seth GS, Chamkha AJ. Transportation of magnetite nanofluid flow and heat transfer over a rotating porous disk with Arrhenius activation energy: Fourth order Noumerov’s method. Chinese J Phys. 2021;69:172-185.

    [Crossref] [Google Scholar]

32. Ali B, Pattnaik PK, Naqvi RA, Waqas H, Hussain S. Brownian motion and thermophoresis effects on bioconvection of rotating Maxwell nanofluid over a Riga plate with Arrhenius activation energy and Cattaneo-Christov heat flux theory. Therm Sci Eng Prog. 2021;23:100863.

    [Crossref] [Google Scholar]

33. Sarwe DU, Shanker B, Mishra R, Kumar RV, Shekar MR. Simultaneous impact of magnetic and Arrhenius activation energy on the flow of Casson hybrid nanofluid over a vertically moving plate. Int J Thermofluid Sci Technol. 2021;8(2):1-20.

    [Crossref] [Google Scholar]

34. Shehzad SA, Hayat T, Alhuthali MS, Asghar S. MHD three-dimensional flow of Jeffrey fluid with Newtonian heating. Journal of Central South University. 2014;21:1428-1433.

    [Crossref] [Google Scholar]

35. Makinde OD, Onyejekwe OO. A numerical study of MHD generalized Couette flow and heat transfer with variable viscosity and electrical conductivity. J Magn Magn Mater. 2011;323(22):2757-2763.

    [Crossref] [Google Scholar]

36. Usman M, Gul T, Khan A, Alsubie A, Ullah MZ. Electromagnetic couple stress film flow of hybrid nanofluid over an unsteady rotating disc. Int Commun Heat Mass Transf. 2021;127:105562.

    [Crossref] [Google Scholar]

37. Bejawada SG, Reddy YD, Jamshed W, Nisar KS, Alharbi AN, Chouikh R. Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium. Alex Eng J. 2022;61(10):8207-8220.

    [Crossref] [Google Scholar]

38. Mogharrebi AR, Ganji ARD, Hosseinzadeh K, Roghani S, Asadi A, Fazlollahtabar A. Investigation of magnetohydrodynamic nanofluid flow contain motile oxytactic microorganisms over rotating cone. Intl J Numer Method Heat Fluid Flow. 2021;31(11):3394-3412.

    [Crossref] [Google Scholar]

39. Mutuku WN, Makinde OD. Hydromagnetic bioconvection of nanofluid over a permeable vertical plate due to gyrotactic microorganisms. Comput Fluids. 2014;95:88-97.

    [Crossref] [Google Scholar]

40. Shah Z, Islam S, Gul T, Bonyah E, Khan MA. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 2018;9:1201-1214.

    [Crossref] [Google Scholar]

41. Attia HA, Kotb NA. MHD flow between two parallel plates with heat transfer. Acta Mechanica. 1996;117(1-4):215-220.

    [Crossref] [Google Scholar]

42. Sheikholeslami M, Ganji DD. Three dimensional heat and mass transfer in a rotating system using nanofluid. Powder Technol. 2014;253:789-796.

    [Crossref] [Google Scholar]