Co-variation in amino acid distribution of any two positions in the multiple sequence alignment (MSA) of a protein family is widely used to obtain structural and/or functional information [1]. It is assumed that, after mutation of one residue, structural/functional constraints can require a compensatory mutation of another residue to maintain the structure or to restore the function of the corresponding protein. Such compensatory mutations can depend on direct physical interactions between two residues or on an indirect interaction through intermediary residues or a ligand [2].

The analysis of sequence co-variation in the MSA of a protein family is not straightforward because the sequences are not independent but phylogenetically related. In the MSA of a protein family containing several sub-families, sub-family independent co-varying positions are assumed to correspond to structurally important compensatory mutations. Subfamily dependent co-varying positions may arise from either compensatory mutations within one sub-family or independent mutations in several subfamilies. Both of these mechanisms lead to a phylogenetic bias.

Until now, the goal of most co-variation studies has been to predict contacts in order to gain structural information from co-evolving positions. To achieve this goal, different methods attempt to remove or reduce the phylogenetic bias [3-5] and to differentiate direct coupling from indirect coupling which is created by the transitivity effect of pair co-variation [2]. To this effect, Bayesian network [2], maximum entropy [6] and neural network [7] models markedly improved the prediction of interacting pairs, with successful de novo 3D protein structure prediction. Recently, co-evolution based methods coupled to machine learning have significantly improved contact prediction and constitute an area of intense research for de novo structure prediction [8]. The analysis of co-varying residues in an MSA has also been used to identify specificity-determining residues [9-12], protein sectors [13] or connectivity pathways [14-16].

Most comparative studies of co-variation methods [3,4,17] aim to find methods that optimize the number of contact pairs to gain structural information. Co-variation approaches that aim to gain information on protein divergence have received less attention. However, these approaches can be very useful to gain information on protein evolution and sub-family specificity. We thus undertook a comparative analysis of widely used co-variation methods on a model system to determine methods best suited to this aim [18].

Characteristics of the model system

To carry out this analysis, we chose the large family of rhodopsin-like G protein coupled receptors as a model system [18]. The human nonolfactory receptor set includes 283 receptors that can be classified into a dozen of sub-families [19] corresponding to three main evolutionary pathways [20]. The median sequence identity of human receptors varies from 20% in the full set to about 30% within sub-families (transmembrane domain only). We compared the different methods on three nested sequence sets. The sets correspond to (1) human non olfactory receptors, (2) receptors characterized by the P2.58 proline pattern (107 members, with 26% sequence identity). The latter receptors diverged after an indel in helix 2 which is one of the main evolutionary pathways of GPCRs [21] and (3) the chemokine receptors (23 members with 37% sequence identity). The characteristics of these three sets are frequently found in a variety of protein families.

Sequence co-variation methods

Most methods that measure co-variation in the amino acid distribution at any two positions in an MSA can be classified into four main classes:

(1) Methods based on the χ² test, such as OMES (Observed minus Expected Squared) [17]. The OMES score is computed as:

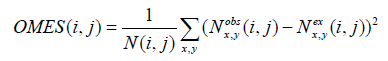
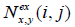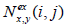where N (i, j) is the number of sequences in the alignment with non-gapped residues at positions i and j, and , are the number of times each pair of amino acids (x,y) is, respectively, observed and expected at positions (i,j). Expectation is based on the frequency of amino acids (x,y) at positions (i,j).

(2) Methods based on mutual information (MI), the probability of joint occurrence of events [22]. The MI score is given by:

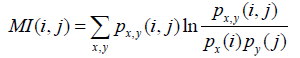
where, p_x (i), p_y (i), and p_{x, y} (i, j) are the frequencies of amino acids x at position i, y at position j and of the pair (x,y) at positions (i,j). As mutual information formula favors pairs with high entropy, several corrections have been applied to correct this bias. The MIp score (mutual information product) outperforms other MI based methods [3] and is computed as:

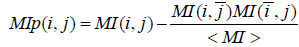
where 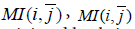and < MI> are the average of MI(i,j) on, respectively, i, j and both i and j.

(3) Methods based on substitution matrices such as McBASC (McLachlan Based Substitution Correlation method) [23]. The McBASC score is computed as:

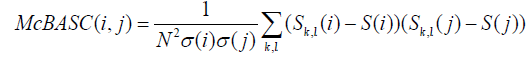
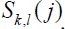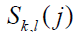where and are the similarity scores based on the McLachlan matrix [24] for the amino acid pair present in sequences k and l at positions i and j, respectively, S(i) and S(j) are, respectively, the averages of all the scores 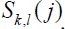and 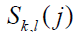and σ(i) and σ(j) are, respectively, the standard deviations of all the scores 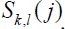and .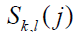

(4) Methods using perturbation of an MSA, such as the statistical coupling analysis (SCA) [16] and Explicit Likelihood of Subset Covariation (ELSC) [25] methods. These latter two methods compare amino acid composition in a subset to the composition in the entire alignment. The SCA score is given by:

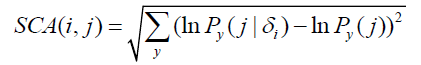
where 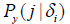is the frequency of amino acid y at position j in the subset defined by the presence of the most prevalent amino acid x at position i.

The ELSC score measures how many possible subsets of size n would have the composition found in column j. It is computed as:

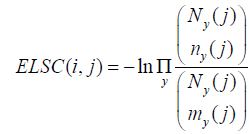
Where 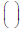is the binomial coefficient.

and N_y (j), n_y (j) and my (j) are, respectively, the numbers of residues y at position j in the total (unperturbed) sequence alignment, in the subset alignment defined by the perturbation in column i and in the ideal subset (i.e., in a subset with the amino acid distribution equal to the total alignment).

Entropy biases

To compare the different methods [18], we analyzed co-variation scores as a function of sequence entropy which is a measure of variability based on the Shannon entropy [26] and is given by:

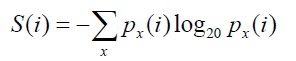
where, i is the position of interest in the MSA, x represents the 20 amino acids and 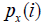represents the frequency of amino acid x at the ith position. To do so, we used bi-dimensional plots. In these plots, each dot represents a pair of positions (i,j) in the MSA and is located at the position of the entropies of i and j, with a color code indicating the co-variation score. The bi-dimensional plots obtained with Set 1 (about 300 sequences) are shown in Figure 1. Similar results were obtained with the other data sets. The MI and SCA methods have strong bias towards pairs with at least one highly variable position (blue dots on right top corner or along right side of the plot) and should thus be considered with caution. The other four methods favor pairs with intermediary conservation (blue dots in the center of the plots). However, with OMES and ELSC, the entropy of the top pairs is clearly separated from the entropy of the bottom pairs (red dots), which is not the case for the MIp and McBASC methods with more fuzzy plots. The plots in Figure 1 clearly indicate that each method favor pairs with different levels of sequence conservation. This entropy bias leads to different results for each method. Consequently, this bias must be taken into account and carefully analyzed upon selection of a method (to do so, we developed the R package bios2cor which includes a function for this bi-dimensional analysis [27]).

Figure 1: Bi-dimensional plots of the co-variation scores as a function of sequence entropy. Each dot represents a pair of positions (i,j) in the MSA. The dot position corresponds to the entropy of i (x axis) and j (y axis) respectively. The color code indicates the co-variation score. Dark and light blue dots indicate the top 25 and 250 pairs respectively. Red and pink dots indicate the bottom 25 and 250 pairs respectively. The analysis was carried out on the transmembrane domain of human nonolfactory class A GPCRs (283 sequences), adapted from [18].

Networking biases

The network representation of the top pairs obtained with the OMES, ELSC, MIp and McBASC methods for Set 1 (Figure 2) highlights another striking difference between methods. MIp and McBASC methods favor pairs with low connectivity whereas the networks obtained with OMES and ELSC have a hub structure with a highly connected central residue. Most importantly, the central residue (P2.58) obtained with the OMES and ELSC methods is an important determinant of GPCR evolution [20,21]. This networking structure is observed for the three nested sequence sets that we have analyzed [18]. In each case, the central residue corresponds to a residue known to be crucial for the evolution of the GPCR family and the sub-family specificity (divergence of purinergic receptors in the set of P2.58 receptors and of inflammatory receptors in the chemokine receptor set). The hub structure observed for GPCRs strongly supports an epistasis model of protein evolution in which after mutation of a key residue, co-evolution of several residues was necessary to restore/shift protein function.

Figure 2: Network representation of the top 25 pairs obtained from co-variation analysis of human non-olfactory class A GPCRs (transmembrane domain only). Positions correspond to nodes and co-variation signals to edges. The size of the nodes is proportional to their connectivity. The color indicates the entropy of the position from black for a fully conserved position to white for the most variable position. Node labels indicate the position with Ballesteros’ numbering [29]. Dotted edges indicate distance below 8 Å. Adapted from [18].

Selection of a co-variation method

The performance of co-variation analysis to answer specific questions crucially depends on (1) the co-variation method used and (2) the characteristics of the MSA (e.g., number of sequences, homogeneity and conservation) [3,4,17]. The first step in a co-variation analysis is thus to determine the specific questions of interest and then, to select a suited co-variation method and to prepare a sequence set accordingly.

When co-variation analysis aims to gain structural information, the methods favoring pairs with low connectivity are suited because these pairs are enriched in contact pairs [3,4]. This is the case for McBASC and MIp (Figure 2). This latter method was specifically developed with this aim. These methods require large sequence sets, with at least 100 sequences, as homogeneous as possible [3,17]. This last requirement should prompt to build MSA of orthologs whenever possible.

When co-variation analysis aims to gain evolutionary information, OMES and ELSC are well suited to identify the co-evolving residues that contributed to the divergence within a protein family. These methods favor pairs with intermediate conservation and highly connected residues and can work with a very small number of sequences (<25). They require a sequence set with two subsets of similar size and sequence similarity. Size requirement can be fulfilled by tailoring sequence sets with judicious use of paralogs and orthologs [18]. Homogeneity of the subsets is mandatory to avoid bias toward an overwhelming or a highly conserved sub-family.

The phylogenetic bias, related to the intrinsic inhomogeneity of a sequence set containing sub-families, represents a rich source of information on the mechanisms that drove the evolution of a protein family. Two co-variation methods, OMES and ELSC, are adequate to mine evolutionary hubs, in relation with an epistasis-based mechanism of functional divergence within a protein family [28].

The R package bios2cor is freely accessible at the Comprehensive R Archive Network (http://cran.r-project.org). It includes R-coded OMES, ELSC, MIp and McBASC functions as well as representation tools, such as the 2D entropy-score plots.

This study was supported by the grant ANR-11-BSV2-026 from the French Research Agency. JP and BT had a fellowship from Conseil Général de Maine-et- Loire and ANR, respectively.