Advanced Techniques in Biology & Medicine
Open Access
ISSN: 2379-1764
ISSN: 2379-1764
Research Article - (2017) Volume 5, Issue 2
The activity cliff concept is of high relevance for medicinal chemistry. Herein, we explore a concept of “data set modelability”, i.e., a priori estimate of the feasibility to obtain externally predictive QSAR models for a data set of bioactive compounds. This concept has emerged from analyzing the effect of so-called “activity cliffs” on the overall performance of QSAR models. Some indexes of “modelability” (SALI, ISAC, and MODI) are known already. We extended the version of MODI to data sets of compounds with real activity values. The predictive efficiency of QSAR models is expressed as the correct classification rate by SVM algorithm, which compared with the results of the other two algorithms: algorithm MODI and Voronin’s algorithm modified by the authors. Comparative analysis of the results performed using Pearson’s correlation coefficient square. Our study showed an extreme lack of evaluation of predictive efficiency of data set only based on “activity cliffs”. In the development of more accurate methods that allow to evaluate the possibility of building of effective models on the data samples, it is necessary to take into account other properties of the sample, and not only the presence (and number) of “activity cliffs”.
Keywords: Models’ efficiency, QSAR, MODI, Activity cliffs
Quantitative structure-activity relationships (QSAR) have been known for many years, however, it can be said that QSAR, as a rule, does not meet expectations in many cases. In principle, the efficiency is determined by the nature of the activity landscape, which is associated with the representation of the chemical space used to describe the set of compounds considered. Activity landscapes have high dimensionality (>3) and depend on:
• The nature of the analysis (e.g. enzymes-based, cell-based, etc.),
• The area (s) of the chemical space from which these compounds are taken,
• Density distribution of compounds in these areas,
• And, most importantly, the molecular representation of compounds.
A typical N-dimensional landscape consists of (N-1)-dimensional chemical space, each dimension is a coordinate determined by a single molecular descriptor or a combination of descriptors. The N-th coordinate is the measured activity of each compounds considered; in three dimensions, activity landscapes are similar to natural landscapes, as shown in Figure 1.
Figure 1: Illustration of the activity landscape with activity cliffs (AC). A. Gradual changes in the structure lead to moderate changes in activity; B. Small changes in the structure lead to strong changes in activity. Reproduced from [9].
For many years, QSAR developed under assumption that similar molecules tend to have similar activity, which makes the activity landscapes look like the gently rolling hills (Figure 1A). However, this picture is not so universal, and in many cases rather resembles a canyon landscape (Figure 1B). In other words, very similar molecules in some cases have very different activities, which in [1] are commonly called activity cliffs (AC). AC is determined by the ratio of the difference in the activity of the two compounds to the "distance" between them in a given chemical space.
In Adilova and Ikramov’s earlier work [2], they investigated a priori estimate of the prognostic efficiency of the sample on the QSAR model for a specific set of bioactive compounds based on the MODI index. It was shown that MODI in some cases weakly reflects the sample ability to be successful in construction of QSAR model. In this paper, another measure of similarity investigated and evaluated its applicability in simulation. It should be noted that molecular similarity is one of the most observed and powerful concepts in chemical informatics [1,3,4]. Many computational methods for estimating the similarity already exist and continue to appear [1,3], but the comparison of compounds and their properties, especially activity, is still one of the most important and often used techniques in chemical and pharmaceutical studies.
To study each approach we chose 5231 compounds from the ChEMBL database with activity against the protein of CA2 (Inhibitory activity against human recombinant carbonic anhydrase II). The original data set divided into samples of 100 and 50 compounds in each. 19 descriptors are given for each compound in CHEMBL, which were used in the calculations.
We used MODI [5] as basic algorithm, which calculates the percentage of pairs of compounds close by descriptors to each other and belonging to the same classes in activity to the total number of compounds. Its goal is to predict efficiency of QSAR models built on this sample as training set.
The index MODI calculates by the formula:

Where K is the number of classes in the sample, 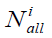 the number of elements in the class
the number of elements in the class 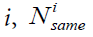 is the number of elements in the class i whose closest neighbor is an element from the same class.
is the number of elements in the class i whose closest neighbor is an element from the same class.
We also used another measure of similarity based on Voronin's approach [6,7] that we have modified. Let the object Ai be described by a set of descriptors 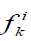 .Then, if the descriptor is a real number, then the similarity of two objects Ai, Aj by this descriptor can be calculated by the formula:
.Then, if the descriptor is a real number, then the similarity of two objects Ai, Aj by this descriptor can be calculated by the formula:
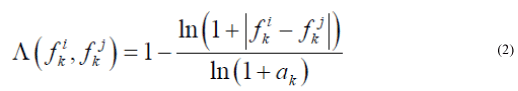
where 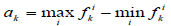
If the descriptor is a binary or has a value in which the concept “more or less” cannot be introduced, then the similarity calculated by the formula:
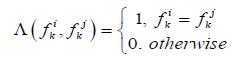 (3)
(3)
The general measure of the similarity of two objects is calculated by the formula:
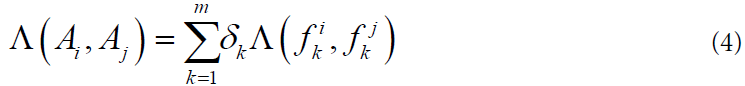
Where the nonnegative coefficients δk are computed on the training sample according to the rule:
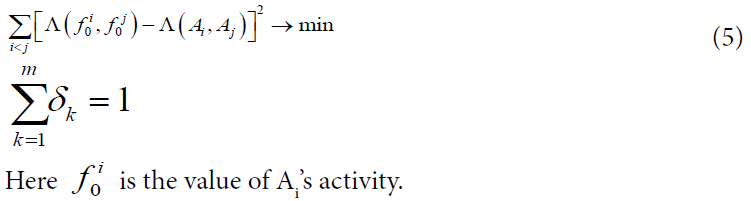
We calculated Voronin’s coefficients and MODI indexes on all the samples (50 and 100 compounds in each, and 200 in addition). It was performed by special programs written in C/C++. The solution of (5) for each data set was found by Microsoft Office Excel 2013.
To validate the QSAR models based on the Voronin similarity measure, it is necessary to establish a threshold, at the excess of which two compounds are considered to be close. Since the measure itself does not set such a parameter, several values were chosen: 0.68, 0.75 and 0.95. These thresholds have been tested during research to obtain optimal value of efficiency prediction.
Further, we studied all compounds close to each other. The number of such pairs whose activity values differ significantly (by 100 units and by 100 times) was counted. It was considered that if only one Voronin coefficient out of the 19 available is equal to 1, then Voronin's method is inapplicable for this sample. It turned out that for samples with 100 compounds Voronin's method is applicable in 98%, and for samples with 50 in 100%. In this case, for MODI, there is no condition of inapplicability of the algorithm.
We trained SVM models on all the samples and then run prediction mode of each model on other samples. We checked the classification results (% of success). The result of the computational experiment is a total of 900 values, so briefly we present here only the maximum, minimum and average values (Table 1).
Next, we calculated the square of the Pearson [8] correlation coefficient between the SVM classification results and the prediction results of the algorithms studied (Table 2).
Then we changed the number of compounds in sets to 200. We got 8 data sets and run the same experiments. Voronin’s algorithm rejected set #2. The results (in %) are presented in the Table 3.
We also calculated Chi-squared coefficients (Table 4). The results showed that Voronin’s algorithm is a better way to predict efficiency values of SVM-models than MODI. But MODI requires less time while calculation of Voronin’s coefficients can be challenging. MODI seeks for the closest compound to be in the same class while our concept of Voronin’s measure looks for all similar compounds around each molecule. It is more general approach and leads to more deep examination of actual “activity landscapes”.
| Algorithm/data set cardinality | Maximum | Average | Minimum |
|---|---|---|---|
| MODI/50 | 40 | 13 | 3 |
| MODI/100 | 27 | 15 | 5.8 |
| SVM/50 | 54 | 23 | 8 |
| SVM/100 | 56 | 26.1 | 8 |
| Voronina (0.68)/50 | 100 | 39 | 0 |
| Voronin (0.75)/50 | 100 | 88 | 0 |
| Voronin (0.95)/50 | 100 | 50 | 0 |
| Voronin (0.68)/100 | 100 | 51 | 0 |
| Voronin (0.75)/100 | 100 | 84 | 0 |
| Voronin (0.95)/100 | 100 | 52 | 0 |
a: The value of the similarity threshold is indicated in parentheses.
Table 1: The maximum, average and minimum values of the success percent obtained on the sample family by different algorithms.
| Pearson's correlation coefficient | MODI | Voronin (0.68) | Voronin (0.75) | Voronin (0.95) |
|---|---|---|---|---|
| Samples of 100 compounds | 0.12 | 0.05 | 0.12 | 0.004 |
| Samples of 50 compounds | 0.06 | 0.03 | 0.01 | 0.03 |
Table 2: Pearson's correlation coefficient between the results of the algorithm SVM classification and prognostic algorithms.
| Set # | MODI | SVM | Voronin (threshold) | ||||
|---|---|---|---|---|---|---|---|
| MIN | MAX | AVER | (0.68) | (0.75) | (0.95) | ||
| 1 | 37.1 | 40.0 | 52.5 | 46.0 | 47.2 | 47.4 | 48.0 |
| 2 | 31.8 | 35.5 | 61.5 | 44.1 | 44.4 | 44.4 | 44.4 |
| 3 | 31.8 | 36.5 | 64.5 | 43.3 | 45.0 | 45.0 | 46.1 |
| 4 | 30.3 | 37.0 | 60.0 | 45.5 | 46.0 | 46.2 | 47.6 |
| 5 | 32.6 | 41.5 | 56.5 | 45.3 | 44.6 | 44.7 | 46.9 |
| 6 | 34.1 | 38.5 | 57.5 | 44.1 | 47.2 | 47.0 | 49.3 |
| 7 | 35.6 | 37.5 | 62.0 | 44.4 | 45.3 | 45.4 | 46.6 |
| 8 | 32.8 | 36.5 | 66.0 | 45.1 | 45.0 | 45.1 | 45.6 |
Table 3: Minimum, maximum, and average values of SVM models’ success compared to MODI and Voronin’s algorithm predictions for data sets of 200 compounds each.
| MODI | Voronin (Threshold) | |||
|---|---|---|---|---|
| (0.68) | (0.75) | (0.95) | ||
| MIN | 0.21 | 0.10 | 0.11 | 0.33 |
| MAX | 0.27 | 0.39 | 0.41 | 0.41 |
| AVER | 0.08 | 0.11 | 0.16 | 0.09 |
Table 4: Pearson's correlation coefficient between the results of the algorithm SVM classification and prognostic algorithms for data sets of 200 compounds each.
| SVM | MODI | Voronin |
|---|---|---|
| 95.8% | 29.6% | 77.3% |
Table 5: Comparing results of SVM and prognostic algorithms based on 500 compounds training sample.
Our first research used Voronin’s measure itself (there were no logarithms in (2)) but it failed to distinguish values like 100 and 2000 as the denominator in (2) was large. Use of logarithms showed better results.
In addition, 500 compounds were randomly selected for the training sample from the set of the 5231 compounds and all other compounds were considered as a test sample. We obtained following results (Table 5).
Thus, both algorithms of a priori estimation of the prognostic efficiency of the sample showed extremely low effectiveness. Their application to the estimation of the sample is limited. It is necessary to develop other methods of more accurately assess the capabilities of classification algorithms on these samples. At the same time, MODI efficiently works on samples of small volume, and the modified Voronin method works better on large samples. It is necessary to take into account these features when developing new methods. The results were presented as abstract in [10].
Funding for this work was provided by the Uzbekistan Committee of Science &Technology under Grant number A-5-1: "Development of computer applications for computer drug design" 2015-2017.