Considering two distant waves; each with mass density ρ are flowing with same velocity v. One of the waves is a rip current with width l₁ with acceleration a and other normal narrower ocean wave with width l₂ with same acceleration a; each with same altitude, h, from sea ground. For same altitude of wave, h₁=h₂;

If l₁>l₂

l₁ Xh >l₂ Xh

A₁>A₂ (where A₁ is surface area of wider continuous wave and A₂ being surface area of narrower wave)

v ×A₁>v × A₂ (For same velocity of continuous wave)

Q₁>Q₂ (As Volumetric Flow rate [1], Q=v XA)

As both waves are in same sea water; the mass density is constant for these two continuous waves (Figure 1):

Figure 1: Comparison between wider and narrower waves in North Sea.

ρ XQ₁>ρ XQ₂

ρ XQ₁ and ρ XQ₂ are mass flow rate [2] for both waves.

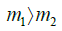(1)

For curved surface area;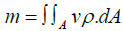

According to Continuum concept of a fluid [3], considering waves are continuous and thus, total mass of a wave would be in effect while considering a point of a wave.

For a surface area, A₃=A₄; where A₃ and A₄ are infinitesimal surface area of consecutively rip wave and normal wave.

Pressure at a point of rip wave,

P1=F1/A3

Pressure at a point of another wave,

P2=F2/A4=F2/A3

From (1); m1>m2

m1 × a>m2 Xa [It was presumed at start of theory that both waves progress with same acceleration a}

(m1 × a)/A3 > (m2 × a)/A3

F1/A3>F2/A3 (As Force=mass × acceleration)

F1/A3>F2/A4

P1>P2

Thus, pressure on a rip current is higher than pressure on normal wave. If P3= 1/2ρv2+P static and P4 are stagnation pressure [4] for rip and normal wave.

Thus, stagnation pressures are given by:

P3>P4

It can be inferred ocean waves with increased continuous surface area can provide higher resistance to a point particle trying to pass through it. Now, assuming electromagnetic waves with high frequency (infinitesimal wavelength between each phase) such as γhard; subjected to infinitesimal wavelength λ and amplitude A. Now, if the surface area that γhard resultant ray covers, the resultant amplitude and connecting length were to increase; each point of γhard would have higher stagnation pressure.

For increasing amplitude; (n-1) constructive interference [5] can be used. Where, n represents number of waves and n>>1 such as the following Figure 2:

Figure 2: Constructive interference engineering to create high amplitude of wave.

Now, considering infinitesimal amplitude increase dx such that

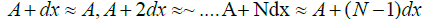
and similarly, in opposite surface;

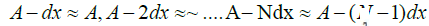
amplitude of γ_hard rays are emitted with same wavelength in such a way that they do not interfere; however, their resultants are so close consecutively that all resultants in effect; act as if a single, much higher surface area-resultant (Figure 3).

Figure 3: Increasing effective surface area.

Now let us consider we are able to move such wave with velocity; it is theorized that such high surface area, increased amplitude and increased connecting wave length with velocity v will have higher stagnation pressure at each existing point of wave for a matter with length>dx to pass through than a wave with lower surface area or naturally occurring γ wave. Thus, such wave in motion; because of its high stagnation pressure; spanning at its’ surface in effect, can make a medium such as air impermeable for aero planes or jets from passing through. If the aerial vehicles’ building materials aren’t strong enough against exerted stagnation pressure, the point of aerial vehicle in contact with the effective surface area of wave will not pass through and the vehicle will be cut into pieces mid-air.

Application proposal for exerting high pressure on aerial vehicles attempting to pass through

To increase amplitude, let us consider n emitters in velocity v of gamma rays positioned as such that they emit gamma rays for increasing amplitude of resultant as shown in Figure 4 and 5. Inside the emitters:

Figure 4: Application proposal.

Figure 5: Connecting length.

Now let us consider a separate set of emitters, also having horizontal velocity v, but within angular distance dθ such that the emitted γhard rays; are at dx distance with previous set of γhard rays. If we consider a third set of γhard rays which have dθ angular distance with second set and 2dθ angular distance with first set of γhard rays in such a way so that the emitted γ hard rays from third set has dx distance with second set and 2dx distance with first set of γhard rays. If we continue this sequence of N set of emitters; with (N-1) dθ angular distance with previous emitter; we will keep on amplifying the final amplitude as well surface area of the total resultant wave where amplitude for each set will be nA and effective surface area of a phase will depend on how many sets of emitters we are considering.

Surface area in effect

Though having dx gap between some particles, the surface area in effect means the surface area which doesn’t let objects with higher length than gap to pass through, as such acting almost as a surface area.

The higher the amplitude of the wave the further up in the sky the gamma ray will cover. With increased surface area in effect, the more area the electromagnetic wave will span. With number of emitters being a very high amount; it is expected that the electromagnetic wave will have a longer connecting length and thus will exert higher stagnation pressure against objects as number of emitters are increased and at a point breaking anything that tries to pass through it.