Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2015) Volume 5, Issue 3
Density, viscosity and refractive index measurements in the T=[288.15 to 303.15] K range of pure chloroform and di-isopropyl ether, as well as of the binary system [x1 chloroform+(1-x1) di-isopropyl ether (DIPE)] over the whole concentration range at T=298.15 K were made. The experimental results for the pure components were fitted to empirical equations. Calculated values are in agreement with the experimental ones. Data of the binary mixture were further used to calculate the excess molar volume, refractive index deviations and viscosity deviations. Excess molar enthalpy at T=(298 ±1) K and vapor-liquid equilibrium measurements at T=(313.15 ±0.05) K were also measured for the binary system. Activity coefficients and the excess molar Gibbs energy are calculated. This binary system shows strong negative deviations from ideality and exhibits a minimum pressure azeotrope, whose coordinates are: P=(32.90 ±0.05) kPa and x1=(0.402 ±0.002). Excess and deviation properties were fitted to the Redlich-Kister polynomial relation. The optimized structures and vibrational frequencies for DIPE, chloroform and their 1:1 complex were calculated by means of density functional theory (DFT) techniques using the B3LYP functional combined with the 6-31G(d,p) basis set. Raman and FT-infrared spectra of pure chloroform (1) and DIPE (2), as well as of the binary system were recorded.. The recorded Raman and FTIR spectra confirm the existence of these type of hydrogen-bonded complexes. The ideal associated solution model was used to calculate the equilibrium constants, which compares well with results obtained from spectroscopic data and the enthalpy of formation of the hydrogen bond.
<Keywords: Association; Intermolecular complexes; Vibrational spectra; Equilibrium constants; (Vapour+liquid) equilibrium; Excess enthalpy
Experimental properties of systems consisting of pairs of liquids are of great practical importance because they are used both to understand the macroscopic behavior and infer structures and interactions as for the design of equipment and methods.
In recent times ethers have received particular attention because they are a possible additive to gasoline and also are used as solvents or reactants in the development of new products. It is for this reason that the knowledge of their properties as well as the mixtures containing is very important to optimize processes in which they are involved.
On the other hand, excess thermodynamic functions and deviations of non-thermodynamic ones of binary liquid mixtures are fundamental to understand the interactions between molecules in this type of mixtures and used as a qualitative and quantitative guide to predict the extent and form of complex formation.
As we assume that the system presents molecular interactions with the formation of hydrogen bond, then perform:
1) Experimental determinations of:
a) Density ρ , refractive index nD and viscosity η in the T=[288.15 to 303.15] K range of pure chloroform and DIPE, as well as for the binary system constituted by these two in the whole mole fraction range at T=(298.15 ±0.01) K.
b) Excess enthalpy at T=(298 ±1) K and vapor-liquid equilibrium (VLE) at T=(313.15 ±0.05) K for this binary system.
From the experimental result for the binary system found empirical equations for density, refractive index and viscosity of both pure components as a function of temperature, as well as for the binary system as a function of composition and were calculated excess functions and deviations from ideality, excess molar volume VE, refractive index deviation ΔnD, viscosity deviations from the ideal behavior Δη, activity coefficients γi, and excess molar Gibbs energy GE.
The excess thermodynamic properties and non-thermodynamic ones were fitted to a Redlich-Kister [1] type equation.
2) The optimized structures and vibrational frequencies for DIPE, chloroform and their 1:1 complexe (as shown in Figure 1) were calculated by means of density functional theory (DFT) techniques using the B3LYP functional combined with the 6-31G(d,p) basis set.
3) Raman and FT-infrared spectroscopic studies were carried out for chloroform, DIPE and the binary system in order to confirm the class and stoichiometry of n-mer and to calculate the equilibrium constants, absorptivities of the monomer bands and enthalpy of formation of the hydrogen bond.
4) We made used of the simplest and more convenient thermodynamic model: the “ideal associated solution model”. We calculate the equilibrium constant and the enthalpy of formation of the hydrogen bond. In the literature for the pure components we have found only, a single job on mixing volumes [2] and two on enthalpy of mixing [3,4].
Materials.
Chloroform (p.a.) and DIPE (p.a.) were supplied by Cicarelli (Argentina) and MERCK (Germany), respectively. To verify the purity of reagents gas chromatography and IR spectroscopy was performed. Infrared spectra of pure components and mixtures were recorded on Perkin Elmer FT-IR Spectrometer – Spectrum RXI, using a KBr sealed cell. A Hewlett Packard 6890 gas chromatograph with an automatic injector (Agilent G2613A) directly connected to a ChemStation (HP G2070AA) with a FID detector. The chemical purities were 0.998 and 0.995 (in mass fraction), respectively. The pure components were stored over 0.3 nm molecular sieves to prevent water absorption and their water contents were periodically checked by Karl Fischer titration using an automatic Mettler DL18 Karl Fischer titrator. These water contents never surpassed 20 ppm.
Experimental Procedure
The same methodology previously applied for mixtures preparation was used in this work [5]. All the weighing were preformed on an electronic balance (Mettler Toledo AG-245) accurate to ±0.1 mg. The uncertainty in the mole fractions is estimated to be lower than ±1.10-4.
Density and viscosity were simultaneously measured with an Anton Paar Stabinger viscometer (SVM 3000/G2) [6] calibrated by the manufacturer. This instrument is equipped with its own Peltier effect control system, which maintains temperature at ±0.01 K. The uncertainties in this work were ±0.3% of the measured viscosity value, ±0.1 kg.m-3 for density, and ±0.01 K for temperature.
Refractive Index was measured with a Leica AR600 refractometer. The temperature was maintained at ±0.01 K with a thermostat Haake D8.
Vapor pressure data were obtained with a commercial equipment (Labodest, model 602-S) available from Fischer Technology, Germany [6]. The observed uncertainties are: ±0.05 K for temperature and ±0.05 kPa for pressure.
Compositions of both conjugated phases for VLE data were determined by density measurements using the above-mentioned equipment. The uncertainty in the mole fractions is estimated to be ±0.001.
Excess enthalpy measurements at atmospheric pressure and at T=(298 ±1) K of the binary system were performed with an adiabatic calorimeter previously described and using the same methodology [7]. The uncertainty in the mole fraction is estimated to be lower than ±0.001 while, for enthalpy of mixing measurements, it is estimated to be lower than 4% of the measured value.
FT-Raman Spectra: Raman absorption spectra at a resolution of 4 cm-1 were recorded using a Thermo Scientific , DX Smart Raman Spectrometer both for pure components and the binary mixtures (3.5 M and 6.2 M; in DIPE and chloroform, respectively, where M denotes concentrations in mol.L-1).
FT-Infrared Spectra: Infrared spectra of pure components and their binary solutions were recorded on Perkin Elmer FT-IR Spectrometer – Spectrum RXI, using a KBr sealed cell with 0.500 mm of path, provided for Perkin Elmer. For this purpose, several highly diluted ternary mixtures were prepared mixing dissimilar masses of both pure, and diluted in CCl4. The concentrations of these ternary solutions were in the range 0.013–0.41 M for both solutes. The infrared spectra of pure components and their binary mixtures were recorded against pure CCl4 as a reference in order to eliminate the absorption bands of the solvent.
Macroscopic properties
The experimental results of the density, viscosity and refractive index of the pure compounds in the T=(273.15 to 318.15) K range, can be seen in Table 1 together with those of literature [5,8-11].
| T/K | ρ /kg. m-3 | n D | η /mPa. s | |||
|---|---|---|---|---|---|---|
| Exp | Lit | Exp | Lit | Exp | Lit | |
| Chloroform | ||||||
| 288.15 | 1497.7 | 1498.45a | 0.62630 | 0.5960a | ||
| 293.15 | 1488.0 | 1489.11a | 1.44572 | 1.44590a | 0.59989 | 0.573d |
| 1487.58b | ||||||
| 298.15 | 1478.4 | 1479.70a | 0.57632 | 0.5357a | ||
| 1477.3c | ||||||
| 303.15 | 1469.2 | 1470.60a | 0.55239 | 0.5140a | ||
| 1469.4d | 0.516d | |||||
| DIPE | ||||||
| 288.15 | 728.6 | 0.32748 | ||||
| 293.15 | 723.4 | 723.9a | 1.36808 | 1.3680a | 0.31545 | 0.3347a |
| 298.15 | 718.2 | 718.5a | 0.30424 | 0.3790a | ||
| 718.32e | 1.36523e | |||||
| 303.15 | 712.9 | 713.5a | 0.28817 | 0.3010a | ||
a Riddick, J. A.; Bunger, W. B.; Sakano, T. K. Organic Solvents. Physical Properties and Methods of Purification. 4th ed.; John Wiley: New York, 1986.
b Kozłowska, M. K.; Domańska, U.; Lempert, M.; Rogalski, M. Determination of Thermodynamic Properties of Isotactic Poly (1-Butene) at Infinite Dilution Using Density and Inverse Gas Chromatography. J. Chromatog. A 1068, 297-305 (2005)
c Atik, Z. Study of Vapor−Liquid Equilibrium for Binary Mixtures (Chloroform + 2,2,2-Trifluoroethanol) and (α,α,α-Trifluorotoluene + 2,2,2-Trifluoroethanol) at Pressure 102 kPa. J. Chem. Eng. Data52, 1128-1130 (2007)
d Clará, R. A.; Gómez Marigliano, A. C.; Sólimo, H. N. Density, Viscosity, Vapor-Liquid Equilibrium, Excess Molar Volume, Viscosity Deviation, and Their Correlations for the Chloroform + 2-Butanone Binary System. J. Chem. Eng. Data51, 1473–1478 (2006)
e Gómez Marigliano, A. C.; Arce, A., Rodil, E., Soto, A. N. Isobaric Vapor-Liquid Equilibriaat 101.32 kPaand Densities, Speeds of Sound, and Refractive Indices at 298.15 K for MTBE or DIPE or TAME + 1-Propanol Binary Systems. J. Chem. Eng. Data55, 92-97 (2010)
Table 1: Density ρ, viscosity η and refractive index nD of pure compounds at several temperatures
Experimental results of density, refractive index and viscosity for the [x1 chloroform+(1-x1) DIPE] binary system in the whole composition range at (298.15 ±0.01) K are listed in Table 2.
| X1 | ρ/kg.m-3 | η/mPa.s | nD |
|---|---|---|---|
| 0 | 718.2 | 0.315 | 1.3681 |
| 0.07 | 751.4 | 0.325 | 1.3703 |
| 0.12 | 777.9 | 0.35 | 1.374 |
| 0.13 | 780.4 | 0.353 | 1.3738 |
| 0.16 | 799.5 | 0.369 | 1.376 |
| 0.21 | 824.2 | 0.39 | 1.3788 |
| 0.21 | 824.1 | 0.39 | 1.3788 |
| 0.26 | 852.5 | 0.413 | 1.3819 |
| 0.31 | 881.9 | 0.437 | 1.3858 |
| 0.35 | 908.3 | 0.458 | 1.3883 |
| 0.35 | 908.2 | 0.458 | 1.3882 |
| 0.4 | 943.8 | 0.484 | 1.3915 |
| 0.46 | 978.3 | 0.507 | 1.3966 |
| 0.5 | 1008 | 0.523 | 1.3994 |
| 0.55 | 1050.3 | 0.543 | 1.4027 |
| 0.55 | 1050.3 | 0.543 | 1.4027 |
| 0.6 | 1082.2 | 0.553 | 1.407 |
| 0.65 | 1126.9 | 0.565 | 1.4103 |
| 0.71 | 1172.1 | 0.572 | 1.4156 |
| 0.76 | 1215.2 | 0.577 | 1.4197 |
| 0.8 | 1257.9 | 0.579 | 1.4237 |
| 0.85 | 1305.6 | 0.581 | 1.4278 |
| 0.9 | 1361.8 | 0.58 | 1.4325 |
| 0.95 | 1420 | 0.579 | 1.4367 |
| 0.95 | 1419.8 | 0.58 | 1.4367 |
| 1 | 1478.4 | 0.576 | 1.4429 |
Table 2: Experimental density ρ, viscosity η refractive index nd data for [x1 chloroform+(1-x1) dipe] binary system at (298.15 ±0.01) K
At least three measurements of these properties were made at each temperature and for each solution or pure component. The experimental results reported in Tables 1 and 2 are averages values.
Polynomial equations were used to correlate the density and viscosity of pure components as a function of temperature and the same properties as a function of mole fraction for the [x1 chloroform+(1-x1) DIPE] binary system:
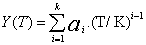 (1)
(1)
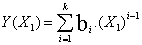 (2)
(2)
where ai and bi are parameters, T is the Kelvin temperature and x1 is the mole fraction of chloroform . Table 3 shows the equations obtained for the pure components as a function of temperature. Table 4 shows the same properties for the binary system as a function of composition together with their standard deviations σ.
| Equations | ρ |
|---|---|
| Chloroform | |
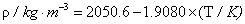 |
0.4kg.m-3 |
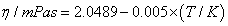 |
0.0005mPa.s |
| DIPE | |
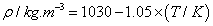 |
0.04 kg×m-3 |
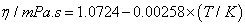 |
0.002 mPa.s |
| Equations | T/K | ρ |
|---|---|---|
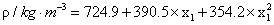 |
298.15 | 4 kg.m-3 |
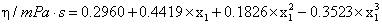 |
298.15 | 5×10-3 mPa.s |
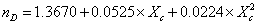 |
298.15 | 5.10-4 |
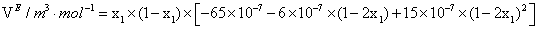 |
298.15 | 1×10-7 m3.mol-1 |
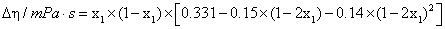 |
298.15 | 3×10-3 mPa.s |
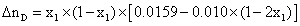 |
298.15 | 2.10-3 |
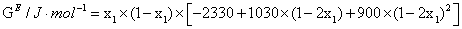 |
313.15 | 30 J.mol-1 |
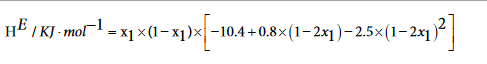 |
298 | 0.05 KJ.mol-1 |
Table 4: Equations for density, viscosity, excess molar and viscosity deviation properties as a function of composition for [x1 chloroform+(1-x1) DIPE] binary system.
Equation 1 and 2 were fitted using a non-linear regression method based on the Levenberg-Marquardt algorithm [12]. with all points equally weighted.
The excess molar volume, refractive index deviations, viscosity deviation, and excess molar Gibbs energy, were calculated with the following expressions:
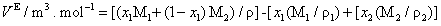 (3)
(3)
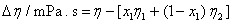 (4)
(4)
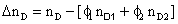 (5)
(5)
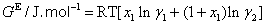 (6)
(6)
where x1 is the mole fraction of chloroform, M1, M2, ρ1, ρ2, nD1, nD2, η1, η2, γ1 and γ2 are the molar masses, densities, refractive indexes, viscosities and activity coefficients the of chloroform and DIPE; respectively, ρ, nD and are the density, refractive index and viscosity of the mixture. The activity coefficients in the liquid phase are related to the vapor-liquid equilibrium by:
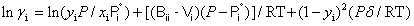 (7)
(7)
Here, yi is the mole fraction of component i in the vapor phase, P and 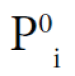 are the total pressure and the pure component vapor pressure, respectively, and Vi is the molar volume of component i. The value of δ is given by
are the total pressure and the pure component vapor pressure, respectively, and Vi is the molar volume of component i. The value of δ is given by
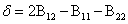 (8)
(8)
where Bij the second virial, estimated at T=313.15 K by the Hayden and O'Connell method [13], are: B11=-1041.947, B22=-1687.182, and B12=-1969.413, all expressed in cm3 mol-1.
Table 5 shows VLE data for the binary system [x1 chloroform+(1-x1) DIPE] at T=(313.15 ±0.05) K. These are thermodynamically consistent according to the point-to-point Van Ness et al. Test [14], as modified by Fredenslund et al. [15], with an average absolute deviation Δy=0.01, and average absolute deviation in pressure ΔP=0.4 kPa, using a treeparameter Legendre polynomial.
| x1 | y1 | P/kPa | γ1 | γ1 | GE/J.mol-1 |
|---|---|---|---|---|---|
| 0.042 | 0.075 | 35.95 | 1.338 | 0.966 | -54.4 |
| 0.054 | 0.09 | 35.66 | 1.239 | 0.954 | -85.8 |
| 0.085 | 0.131 | 35.17 | 1.13 | 0.93 | -145.8 |
| 0.107 | 0.154 | 34.88 | 1.047 | 0.92 | -181.1 |
| 0.134 | 0.182 | 34.4 | 0.975 | 0.905 | -233.9 |
| 0.157 | 0.204 | 34.16 | 0.927 | 0.898 | -267.1 |
| 0.19 | 0.24 | 33.7 | 0.889 | 0.881 | -325.4 |
| 0.231 | 0.269 | 33.4 | 0.813 | 0.885 | -369.1 |
| 0.249 | 0.283 | 33.3 | 0.791 | 0.886 | -388.7 |
| 0.268 | 0.299 | 33.2 | 0.774 | 0.886 | -409.4 |
| 0.274 | 0.302 | 33.15 | 0.764 | 0.888 | -416.6 |
| 0.293 | 0.317 | 33.05 | 0.748 | 0.89 | -436 |
| 0.302 | 0.325 | 33.03 | 0.743 | 0.89 | -445.4 |
| 0.323 | 0.34 | 32.98 | 0.726 | 0.896 | -462.8 |
| 0.348 | 0.359 | 32.91 | 0.71 | 0.902 | -485.4 |
| 0.376 | 0.377 | 32.9 | 0.69 | 0.915 | -507.6 |
| 0.405 | 0.398 | 32.92 | 0.677 | 0.928 | -527.1 |
| 0.422 | 0.409 | 32.93 | 0.668 | 0.938 | -539.6 |
| 0.454 | 0.432 | 33 | 0.657 | 0.956 | -560.5 |
| 0.504 | 0.466 | 33.28 | 0.644 | 0.998 | -580 |
| 0.575 | 0.512 | 33.87 | 0.631 | 1.082 | -602.1 |
| 0.585 | 0.518 | 34.06 | 0.631 | 1.101 | -597.4 |
| 0.631 | 0.551 | 34.55 | 0.631 | 1.169 | -606.4 |
| 0.674 | 0.582 | 35.25 | 0.637 | 1.256 | -597.9 |
| 0.72 | 0.614 | 36.22 | 0.646 | 1.386 | -581.2 |
| 0.769 | 0.656 | 37.38 | 0.667 | 1.543 | -549.9 |
| 0.815 | 0.7 | 38.61 | 0.693 | 1.733 | -513.3 |
| 0.862 | 0.751 | 40.28 | 0.733 | 2.008 | -446.6 |
| 0.9 | 0.8 | 41.94 | 0.778 | 2.312 | -370 |
| 0.936 | 0.86 | 44.16 | 0.846 | 2.656 | -244.8 |
| 0.968 | 0.924 | 45.85 | 0.912 | 2.986 | -141 |
Table 5: Experimental results for the mole Fraction of chloroform in the liquid x1 and vapor y1 equilibrium phases, total pressure P, calculated activity coefficients γi and the excess molar gibbs energy GE for [x1 chloroform+(1- x1) DIPE] binary system at T=(313.15 ±0.05) K
Table 6 shows the excess molar enthalpy HE of the binary system [x1 chloroform+(1-x1) DIPE] as a function of the mole fraction of chloroform at T=(298 ±1) K.
| x1 | HE/ kJ .mol-1 |
|---|---|
| 0 | 0 |
| 0.034 | -0.42 |
| 0.091 | -0.94 |
| 0.141 | -1.41 |
| 0.236 | -1.85 |
| 0.272 | -2.09 |
| 0.398 | -2.44 |
| 0.413 | -2.55 |
| 0.539 | -2.6 |
| 0.625 | -2.55 |
| 0.754 | -2.12 |
| 0.828 | -1.65 |
| 0.856 | -1.56 |
| 0.876 | -1.29 |
| 0.901 | -1.08 |
| 0.952 | -0.72 |
| 0.981 | -0.2 |
| 1 | 0 |
Table 6: Experimental results for the molar enthalpy HE for [x1chloroform+(1-x1) DIPE] binary system at T=(298 ±1) K
Excess thermodynamic functions and deviations from ideality were fitted by means of a Redlich-Kister type equation1.
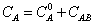 (9)
(9)
where YE represents either VE, ΔnD, Δη, HE or GE. The corresponding equations are shown in Table 4, together with the standard deviation σ, defined as:
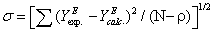 (10)
(10)
where N and p are the experimental point and parameter numbers, respectively.
In all correlation equations the number of constants and the appropriate number of significant digits are selected taking into account the experimental uncertainty reported above for each measured property, obtaining a good agreement with experimental data within experimental error.
Figures 2 and 3 show the excess molar volume and viscosity deviations plotted against the mole fraction of chloroform at 298.15 K, respectively, while Figure 4 shows the total vapor pressure P, liquidphase x1, and vapor-phase y1 mole fraction measurements, plotted against the mole fraction of chloroform at 313.15 K.
Figure 4:
Figure 4: Isothermal VLE for [x1 chloroform+(1- x1) DIPE] binary system at T=313.15 K. ○, vapor phase; ■ liquid phase. Error bars are hidden within the signs. Figure 5: and 6 show the excess molar Gibbs energy GE and excess molar enthalpy HE, against x1 at 313.15 K and 298.15 K respectively. As shown GE, HE, and VE are negative over the entire concentration range, with a minimum close to x1=0.5.Figure 5 and 6 show the excess molar Gibbs energy GE and excess molar enthalpy HE, against x1 at 313.15 K and 298.15 K respectively. As shown GE, HE, and VE are negative over the entire concentration range, with a minimum close to x1=0.5.
Figure 5: Excess molar enthalpy HE against x1 for [x1 chloroform+(1- x1) DIPE] binary system at 298.15 K, ■ this work; ○ from ref (4). Solid lines correspond to the least squares fit using eq. 9, ▲calculated for ideal associated solution model and Ι error bar. Some error bars are hidden within the signs
The concentration dependence of these excess properties indicates that the interactions between unlike molecules in the mixture are stronger than between like molecules in the pure liquids and association forces dominate the mixing process.
It is known that systems with strong interactions between molecules exhibit positive viscosity deviations [16-17]. Figure 3 shows that the viscosity deviation is positive over the whole composition range. On the other hand, ΔnD close to or greater than 0.004 are indicative of complex formation [18-20]. This system presents ΔnD values higher than 0.04. Figure 4 shows that this binary system has negative deviations from ideal behavior and Figure 5 shows that this binary system exhibits an exothermic behavior. This behavior was already observed by other researchers [3,4].
From this result we can conclude that association is the dominant process in this system.
Theoretical calculations
The optimized structures and vibrational frequencies for DIPE, chloroform and their 1:1 complex were calculated by means of density functional theory (DFT) techniques using the B3LYP functional [21,22] combined with the 6-31G(d,p) basis set. Although MP2 [23] method is preferred to the B3LYP one regarding binding energies, the same tendency can be observed in B3LYP calculations with the advantage of lowering the computational cost [24]. All calculations were made for the isolated species using the Gaussian 03 set of programs [25].
For both levels of theory, the geometry was fully optimized with C3V symmetry for chloroform and without symmetry constraints for DIPE and their complex. The frequency calculation confirmed that all the structures are global minimum on the potential surface.
Theoretical frequencies, infrared intensities and Raman scattering were used to simulate the experimental spectra. The vibrational frequencies of DIPE, chloroform and their complex calculated with the B3LYP/6-31G(d,p) combination were multiplied by the factor 0.9613 [26] to better reproduce the experimental data. No anharmonicity corrections of these frequencies were made because of lack of necessary experimental data. These calculated values appear in Table 7 along with the frequencies observed in the infrared and Raman spectra.
| Mode a | DIPE Exp | Chloroform Exp | DIPE+Chloroform Exp | ||||||
|---|---|---|---|---|---|---|---|---|---|
| IR | Raman | Calc.c | IR | Raman | Calc.c | IR | Raman | Calc.c | |
| ν C-H | 3020.55 | 3016.48 | 3068.62 | 3016.05 (f) | 3016.84 (f) | 3014.76 | |||
| 2992.09 (b) | 2992.21 (b) | ||||||||
| ν CH3antisym | 2973.32 | 2978.98 | 3005.29 | 2979.31 | 2972.50 | 3012.50 | |||
| 2950.18 | 2970.63 | 2997.36 | 2967.44 | 2949.19 | 3006.73 | ||||
| 2934.00 | 2936.04 | 2992.40 | 2934.26 | 2935.42 | 3001.50 | ||||
| 2918.63 | 2919.03 | 2983.47 | 2928.23 | 2918.97 | 2996.57 | ||||
| ν CH3sym | 2901.67 | 2914.77 | 2923.99 | ||||||
| 2876.72 | 2878.13 | 2916.16 | 2897.05 | 2902.28 | 2933.98 | ||||
| 2843.34 | 2867.30 | 2886.87 | 2876.63 | 2882.57 | 2927.11 | ||||
| 2833.15 | 2850.06 | 2879.57 | 2849.07 | 2867.88 | 2898.88 | ||||
| 2830.79 | 2851.74 | 2887.49 | |||||||
| ρ CCl3 | 1216.13 | 1213.80 | 1201.10 | 1220.21 (b) | 1227.62 (b) | 1278.12 | |||
| 1217.94 (f) | 1215.71 (f) | ||||||||
| 1215.13 | 1213.21 | 1201.09 | 1216.08 (f) | 1213.98 (f) | 1253.03 | ||||
| 1214.18 (b) | 1204.99 (b) | ||||||||
| ρ C-C | 1188.72 | 1187.49 | 1171.49 | 1189.19 | 1187.61 | 1176.15 | |||
| 1168.32 | 1163.76 | 1150.40 | 1168.16 | 1168.14 | 1152.81 | ||||
| 490.03 | 490.26 | 490.15 | 489.87 | ||||||
| ν CO sym. | 796.01 | 792.85 | 746.13 | 796.95 (b) | 795.00 (b) | 774.60 | |||
| 791.05 (f) | 791.70 (f) | ||||||||
| ν C-O antisym. | 1013.14 | 1011.74 | 926.53 | 1013.80 (f) | 1006.71 (f) | ||||
| 1009.07 (b) | 1002.86 (b) | 993.66 | |||||||
| Combination | 1158.18 | 1155.54 | 1123.22 | 1180.80 (b) | 1176.03 (b) | 1140.74 | |||
| ν C-C + δ C-C, | 1158.45 (f) | 1154.51 (f) | |||||||
| δ C-O+ δ C-H | 1139.05 | 1130.75 | 1098.73 | 1140.50 | 1137.29 | 1106.10 | |||
| 1126.10 | 1123.25 | 1093.79 | 1126.12 | 1123.52 | |||||
| 1109.90 | 1106.26 | 1064.64 | 1109.88 (f) | 1110.80 (f) | 1088.08 | ||||
| 1100.16 (b) | 1102.28 (b) | ||||||||
| ν CCl3 antisym. | 764.22 | 760.80 | 708.32 | 774.64 (b) | 771.49 (b) | 701.00 | |||
| 765.51 (f) | 763.24 (f) | ||||||||
| 761.14 | 755.85 | 708.31 | 756.82 (f) | 752.20 (f) | 698.77 | ||||
| 744.95 (b) | 745.20 (b) | ||||||||
| ν CCl3 sym. | 670.23 | 665.04 | 639.76 | 670.13 (f) | 665.95 (f) | 632.85 | |||
| 668.84 (b) | 662.78 (b) | ||||||||
| ρ CO | 452.15 | 459.50 | 487.07 (b) | 417.19 | |||||
| 478.15 (f) | |||||||||
| δ CCl3 sym. | 363.06 | 352.67 | 362.86 (f) | 352.94 | |||||
| 357.46 (b) | |||||||||
| δ CCl3 | 259.74 | 250.68 | 265.78 (b) | 251.74 | |||||
| 258.70 (f) | |||||||||
| 256.32 | 250.67 | 255.35 (f) | 250.89 | ||||||
| 246.86 (b) | |||||||||
aν, stretching; δ, deformation; ρ rocking.
bf represents free. b bonded, in parentheses.
Table 7: Experimental and calculated frequencies (in cm-1) for Dipe, chloroform and complex
Spectroscopic studies
IR spectra for the pure components and their mixtures in different concentrations, diluted in a solvent "inert" (from the point of view of interaction by hydrogen bonding) and Raman spectra for the pure components and one mixture were performed.
Figure 7 shows the Raman spectra at T=293 K of pure chloroform and DIPE, together with one binary mixture with a concentration (3.5M and 6.2M in DIPE and chloroform, respectively). It is observed that there are significant differences between the spectra of the pure components and the mixture.
In the CH stretching region around 3000 cm-1 the pure chloroform has a very intense band at 3017 cm-1, assigned to the CH stretching vibrational mode of free molecules (monomers), which remarkably decreases when this chemical is mixed with DIPE and a new band appears at 2992 cm-1 which is attributed to the hydrogen-bonded species. Pure DIPE presents several bands around 2900 cm-1, which are assigned to symmetric and asymmetric stretching modes of the methyl groups. The shape of the band is not significantly affected, but the intensity changes due to dilution
From the above observations, we conclude that the CH group of the chloroform molecule is directly involved in the formation of a hydrogen-bonded complex, as occurs for the system chloroformx butanone [27].
In the COC stretching zone are two bands at approximately 750 cm-1 (strong) and 1000 cm-1 (very weak) corresponding to the symmetric and antisymmetric stretching respectibely for pure DIPE. The shape of the COC stretching band is significantly modified when DIPE is mixed with chloroform. As we can see the change in shape suggests the presence of new bands underneath it. Using the same methodology previously applied in other studies curve fitting is performed in both bands [27]. The most appropriate set corresponds to two bands in each, whose maximums are located at 791 cm-1- 794 cm-1 and 1007 cm- 1-1003 cm-1, which were assigned to the symmetric and antisymmetric stretching to the COC the monomer and dimer respectively.
Infrared spectra were recorded at highly dilution of both components and the different mixtures, using CCl4 as solvent. IR spectra show a similar behavior to that observed for Raman.
When comparing the results of the theoretical calculations with IR and Raman spectra, both frequencies and intensities show obvious similarities. This is conclusive evidence of AB complex formation between unlike molecules in this binary system. Therefore the chloroform (A) and DIPE (B) are in chemical equilibrium with the complex (AB), represented by reactions (11).
A+B → AB (11)
The equilibrium constants for these reactions in terms of molar concentrations KD, may be written as
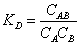 (12)
(12)
where KD is the association constant, and Ci the concentrations of the species present.
Macroscopic molar concentrations CA is
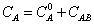 (13)
(13)
where 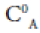 is the monomer concentration of chloroform and CAB is the concentration of dimers formed in the mixing process. Using Beer's law A= a0.L.C and (12) in (13)
is the monomer concentration of chloroform and CAB is the concentration of dimers formed in the mixing process. Using Beer's law A= a0.L.C and (12) in (13)
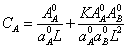 (14)
(14)
Where 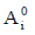 are the absorbances and
are the absorbances and 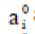 are the absorptivities of the monomeric species corresponding to the bands under study, and L is the optical path. Absorptivities (of the monomer bands) are obtained from the spectrum of the pure components diluted in CCl4 . All spectra are always performed under the same conditions of temperature and pressure.
are the absorptivities of the monomeric species corresponding to the bands under study, and L is the optical path. Absorptivities (of the monomer bands) are obtained from the spectrum of the pure components diluted in CCl4 . All spectra are always performed under the same conditions of temperature and pressure.
Using the same process of curve fitting the CH stretching bands of chloroform and CO stretch of DIPE in the IR spectra of the pure components and mixtures could be calculated absorptivities and the equilibrium constant.
The absorptivity value for CO stretch of DIPE is (17000 ±1000) dm2.mol-1 and the CH stretching bands of chloroform is the same result we obtained in a previous work [27]. The KD values at T=293.15 K, evaluated through eq (12), is (2.9 ±0.1) L mol-1.
On the other hand, KD, in term of molar concentration is related to K, in term of mole fractions, by
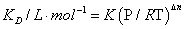 (15)
(15)
where P, R, and T are the normal pressure (1 atm), universal gas constant ( 0.08206 L.atm.mol-1.K-1), and absolute temperature ( 293 K), respectively, while Δn=-1 for dimer formation, that leads to:
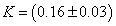
The ideal associated solution model was also applied, the simplest case, as this system. The total heat of formation (hT, f) for this model and for this situation (unassociated pure compounds and in the mixture with associations in a 1:1) is obtained from the expression;
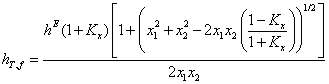 (16)
(16)
The heat of formation (hT, f) values at T=293.15 K, evaluated through equation (16),
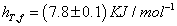
Comparing the thermodynamic results with those calculated by the model of ideal associated solutions from spectroscopic data, we can conclude that, within experimental error, the model is applicable as shown in Figure 5.
Empirical equations of density, refractive index and viscosity were deduced, to estimate these properties both for pure and mixed components within the reported standard deviations. Calculated values are in agreement with the experimental results, within the experimental error
Isothermal vapor-liquid equilibrium data of the binary system were obtained at T=313.15 K, showing negative deviations from Raoult's law and a minimum pressure azeotrope.
From the measured properties, excess functions and deviations from ideality are calculated and it can be seen that all excess properties and deviations from ideality lead to the conclusion that there is an association between different molecules and it can be assumed an 1:1 stoichiometry.
The IR and Raman spectrum show agreement with the theoretical calculations from the proposed interaction model. There is an association by hydrogen bonding with AB stoichiometric relationship. This conclusion was obtained analyzing the IR and Raman spectrum of chloroform, DIPE, and mixtures together with quantum chemical calculations with DFT procedures.
Furthermore, the ideal associated solution model is able to represent the experimental excess molar enthalpy, as we can see in Figure 5 that leads to equilibrium constants values well comparable with that calculated from infrared spectroscopy.
Financial support from the Consejo de Investigaciones de la Universidad Nacional de Tucumán of Argentina, through Grant 26/E516, is gratefully acknowledged. As well as the doctoral fellowship granted by CONICET to R.N.Medina Naessens.